数学苏教版(2019)必修第一册 3.2.1基本不等式的证明课件(共26张PPT)
文档属性
| 名称 | 数学苏教版(2019)必修第一册 3.2.1基本不等式的证明课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 21:41:47 | ||
图片预览





文档简介
基本不等式
第三单元 第二节
情景导入
新课教授
例题讲解
课后作业
情景导入
1
情景导入
生活中的不等关系
10元钱吃早饭,你会怎么选?
A.两个肉松面包 + 一杯牛奶 (8元)
B.一份米粉 (6元)
C.麦当劳的一份早餐套餐 (10元)
比较:价钱谁贵谁便宜?营养谁多谁少?
同学们:比较事物间的相等关系和不相等关系是我们一种天生的非常重要的逻辑思维能力,在我们的数学中存在许许多多的相等关系和不相等的关系,例如:
正数 负数
其实这样的相等关系和不相等关系还有很多,今天,让我们一起去探索两个非常重要的不等关系。
新课教授
2
新课教授
数学学习中的不等关系
图1
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
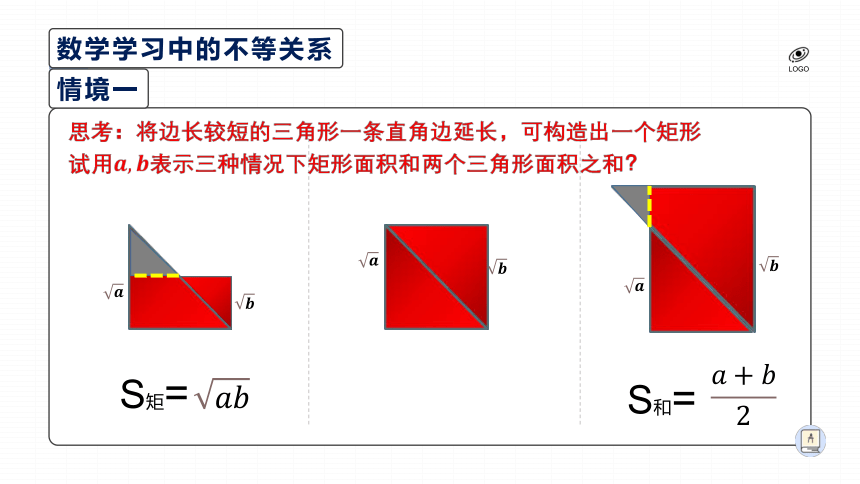
情境一
新课教授
数学学习中的不等关系
????
?
????
?
????
?
????
?
????
?
????
?
????
?
情境一
S矩=
????????
?
S和=
????+????2
?
新课教授
数学学习中的不等关系
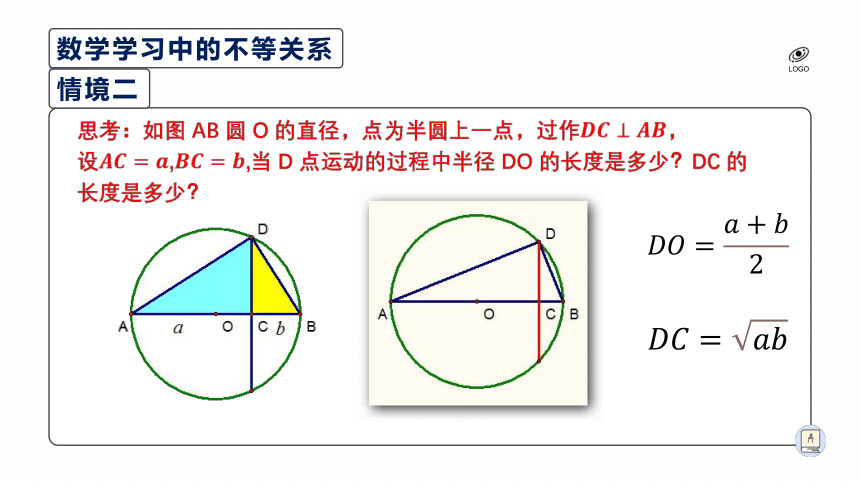
情境二
????????=????+????2
?
????????=????????
?
新课教授
数学学习中的不等关系
问:这两个问题中都涉及了哪两个量?
????+????????
?
????????
?
问:结合几何图形的动态变化过程,你认为算术平均数和几何平均数之间有怎样的大小关系?
新课教授
数学学习中的不等关系
问题1中矩形的面积不超过两个三角形的面积之和,所以
????????≤????+????????
?
????????≤????+????????
?
问题2中当点D在圆周上运动时总有半径不小于半弦,所以
新课教授
数学学习中的不等关系
新课教授
数学学习中的不等关系
证明:要证
只要证
只要证
只要证
分析法
显然, 是成立的.当且仅当a=b时, 取等号.
新课教授
数学学习中的不等关系
证明:
综合法
?
?
?
?
?
?
在证明不等式时,我们通常用分析法来寻找思路,用综合法来书写过程。
新课教授
数学学习中的不等关系
如果把????,????是正数的条件放宽至????≥????,????≥????,该不等式也是成立的。
?
基本不等式
代数意义:两个正数的算术平均数不小于它们的几何平均数.
几何意义:半径不小于半弦。
新课教授
数学学习中的不等关系
推论:两个重要不等式
重要不等式1:
重要不等式2:
????????≤????+????????????
?
新课教授
数学学习中的不等关系
问题:基本不等式和重要不等式的联系与区别吗?
a=b
a=b
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
a,b∈R
a>0,b>0
数学学习中的不等关系
例题讲解
3
基本知识点巩固
判断题
例1:请判断下列表述的正误。
(基本不等式的适用范围)
(基本不等式的取等条件)
(基本不等式的灵活使用)
×
×
计算题
证明 ∵x,y都是正数,
当且仅当x=y时,等号成立.
计算题
证明 ∵x,y都是正数,
当且仅当????=????????,????=?????????,x=y=1时,等号成立.
?
例2(2)已知x,y都是正数.求证:????+????+????????+????????≥????;
?
所以,????+????+????????+????????≥????
?
计算题
解: ∵x>-2,
例3.已知函数????=????+????????????+????,????∈?2,+∞?求函数的最小值;
?
当且仅当,????+????=????????+????,即????=????时等号成立
?
规律与方法
2. 在利用基本不等式证明的过程中,常需要把数、式合理地拆成两项或多项或把恒等式变形配凑成适当的数、式,以便于利用基本不等式.
课后作业
4
认真思考
课后作业
教材 66页习题3 、4
谢谢
OfficePLUS
第一单元
第三单元 第二节
情景导入
新课教授
例题讲解
课后作业
情景导入
1
情景导入
生活中的不等关系
10元钱吃早饭,你会怎么选?
A.两个肉松面包 + 一杯牛奶 (8元)
B.一份米粉 (6元)
C.麦当劳的一份早餐套餐 (10元)
比较:价钱谁贵谁便宜?营养谁多谁少?
同学们:比较事物间的相等关系和不相等关系是我们一种天生的非常重要的逻辑思维能力,在我们的数学中存在许许多多的相等关系和不相等的关系,例如:
正数 负数
其实这样的相等关系和不相等关系还有很多,今天,让我们一起去探索两个非常重要的不等关系。
新课教授
2
新课教授
数学学习中的不等关系
图1
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
情境一
新课教授
数学学习中的不等关系
????
?
????
?
????
?
????
?
????
?
????
?
????
?
情境一
S矩=
????????
?
S和=
????+????2
?
新课教授
数学学习中的不等关系
情境二
????????=????+????2
?
????????=????????
?
新课教授
数学学习中的不等关系
问:这两个问题中都涉及了哪两个量?
????+????????
?
????????
?
问:结合几何图形的动态变化过程,你认为算术平均数和几何平均数之间有怎样的大小关系?
新课教授
数学学习中的不等关系
问题1中矩形的面积不超过两个三角形的面积之和,所以
????????≤????+????????
?
????????≤????+????????
?
问题2中当点D在圆周上运动时总有半径不小于半弦,所以
新课教授
数学学习中的不等关系
新课教授
数学学习中的不等关系
证明:要证
只要证
只要证
只要证
分析法
显然, 是成立的.当且仅当a=b时, 取等号.
新课教授
数学学习中的不等关系
证明:
综合法
?
?
?
?
?
?
在证明不等式时,我们通常用分析法来寻找思路,用综合法来书写过程。
新课教授
数学学习中的不等关系
如果把????,????是正数的条件放宽至????≥????,????≥????,该不等式也是成立的。
?
基本不等式
代数意义:两个正数的算术平均数不小于它们的几何平均数.
几何意义:半径不小于半弦。
新课教授
数学学习中的不等关系
推论:两个重要不等式
重要不等式1:
重要不等式2:
????????≤????+????????????
?
新课教授
数学学习中的不等关系
问题:基本不等式和重要不等式的联系与区别吗?
a=b
a=b
两个正数的算术平均数不小于它们的几何平均数
两数的平方和不小于它们积的2倍
a,b∈R
a>0,b>0
数学学习中的不等关系
例题讲解
3
基本知识点巩固
判断题
例1:请判断下列表述的正误。
(基本不等式的适用范围)
(基本不等式的取等条件)
(基本不等式的灵活使用)
×
×
计算题
证明 ∵x,y都是正数,
当且仅当x=y时,等号成立.
计算题
证明 ∵x,y都是正数,
当且仅当????=????????,????=?????????,x=y=1时,等号成立.
?
例2(2)已知x,y都是正数.求证:????+????+????????+????????≥????;
?
所以,????+????+????????+????????≥????
?
计算题
解: ∵x>-2,
例3.已知函数????=????+????????????+????,????∈?2,+∞?求函数的最小值;
?
当且仅当,????+????=????????+????,即????=????时等号成立
?
规律与方法
2. 在利用基本不等式证明的过程中,常需要把数、式合理地拆成两项或多项或把恒等式变形配凑成适当的数、式,以便于利用基本不等式.
课后作业
4
认真思考
课后作业
教材 66页习题3 、4
谢谢
OfficePLUS
第一单元
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
