9.1.1正弦定理第1课时正弦定理课件(共36张PPT) 数学人教B版(2019)必修第四册
文档属性
| 名称 | 9.1.1正弦定理第1课时正弦定理课件(共36张PPT) 数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 626.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览



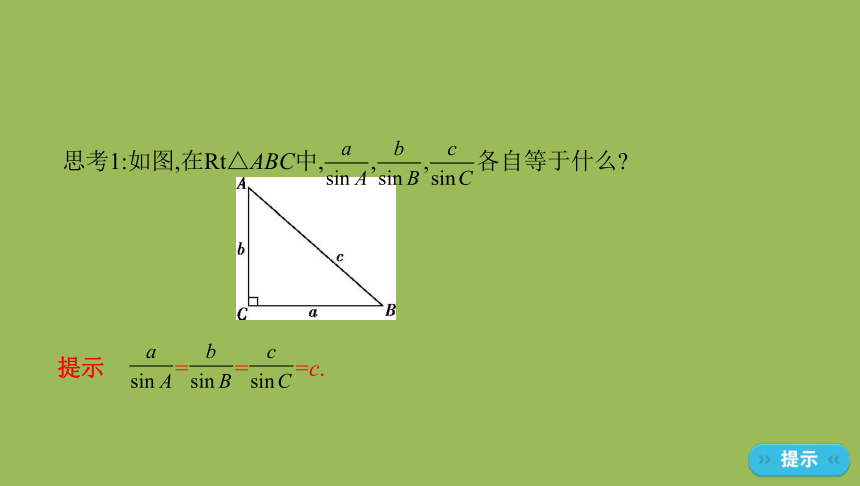




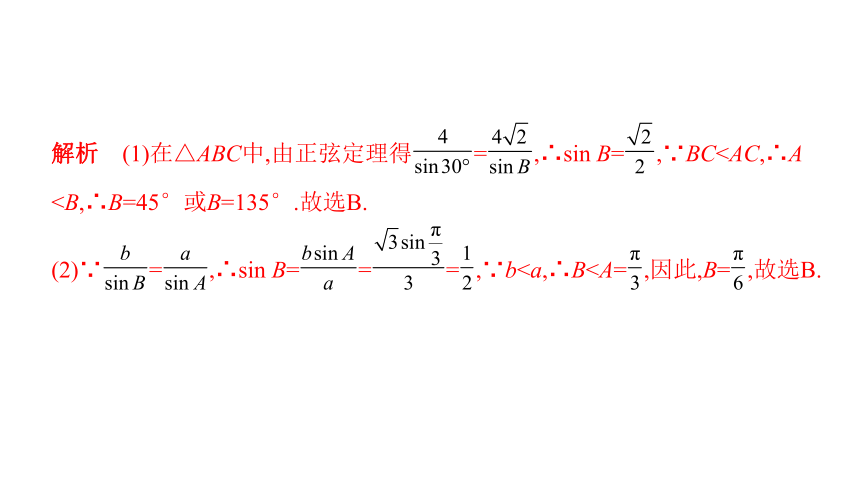



文档简介
第九章 解三角形
§9.1 正弦定理与余弦定理
9.1.1 正弦定理
第一篇 教材过关
第1课时 正弦定理
情景导学
精读教材·必备知识
正弦定理是由伊朗著名的天文学家阿布尔·威发(940—998)首先发现与证明
的.中亚细亚人阿尔比鲁尼(973—1048)给三角形的正弦定理做出了一个证明.
也有说正弦定理的证明是13世纪的那希尔丁在《论完全四边形》中第一次把
三角学作为独立的学科进行论述,首次清楚地论证了正弦定理.至此三角学开
始脱离天文学,走上独立发展的道路.本节将学习三角学中的正弦定理.
1.正弦定理
在一个三角形中,各边的长和它所对角的正弦的比①______.
其公式为②??????.
教材研读
相等
提示?????=?=?=c.
思考1:如图,在Rt△ABC中,?,?,?各自等于什么?
?
2.正弦定理的常见变形
(1)sin A∶sin B∶sin C=③________;
(2)?=?=?=?=2R(R为△ABC外接圆半径);
(3)a=④______,b=⑤ ______,c=⑥ ______;
(4)sin A=⑦???,sin B=⑧????,sin C=⑨????.
a∶b∶c
2Rsin A
2Rsin B
2Rsin C
思考2:在△ABC中,已知acos B=bcos A.你能用角把等式中的边a,b表示出来吗?
提示 可借助正弦定理把边化成角:2Rsin Acos B=2Rsin Bcos A,移项后就是一个三角恒等变换公式sin Acos B-cos Asin B=0.
3.解三角形
习惯上,我们把三角形的?_____与?_____都称为三角形的元素,已知三角形
的若干元素求?________一般称为解三角形.
思考3:利用正弦定理可以解决哪两类有关三角形的问题?
3个角
3条边
其他元素
提示 ①已知两角和任意一边,求其他两边和第三个角;
②已知两边和其中一边的对角,求另一边的对角,从而求出其他的边和角.
互动探究·关键能力
探究一????已知两边及一边的对角解三角形
例1 (1)(易错题)(2019辽宁凌源二中期末)在△ABC中,若A=30°,BC=4,AC=4
?,则角B为?( )
A.45° ????B.45°或135°
C.60° ????D.135°
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若a=3,b=?,A=?,则B= ?(???? )
A.? ????B.? ????C.? ????D.?或?
B
B
解析 (1)在△ABC中,由正弦定理得?=?,∴sin B=?,∵BC(2)∵?=?,∴sin B=?=?=?,∵b易错点拨
(1)由正弦值得出角的大小时注意判断所得出的角的大小是否满足条件,避免
漏解或多解.
(2)已知三角形的两边和其中一边的对角解三角形时的方法:
首先,由正弦定理求出另一边对角的正弦值.
其次,如果已知的角为大边所对的角,那么由三角形中“大边对大角,大角对大
边”能判断另一边所对的角为锐角,由正弦值可求唯一的锐角;如果已知的角
为小边所对的角,那么不能判断另一边所对的角是不是锐角,这时由正弦值可
求出两个角.
跟踪训练
1-1 在△ABC中,a=2,b=?,B=?,则sin A的值是?( )
A.? ????B.?
C.? ????D.?或?
B
解析 由正弦定理得?=?,∴sin A=?·sin ?=?,故选B.
1-2 设△ABC的内角A、B、C所对的边分别为a、b、c,若a=3,b=?,A=?,则
B=?( )
A.? ????B.?或?
C.? ????D.?或?
A
解析 由正弦定理得sin B=?
=?=?,
又b故选A.
探究二 已知两角及一边解三角形
例2 在△ABC中,角A,B,C的对边分别为a,b,c,A=45°,B=120°,a=6,则b=?( )
A.2? ????B.3? ????C.3? ????D.3?
D
解析 ∵?=?,∴b=?=?=3?.故选D.
变式训练
(变结论)若例2中的条件不变,求c的值.
解析 ∵A=45°,B=120°, ∴C=15°.
∴sin C=sin 15°=sin(45°-30°)=sin 45°·cos 30°-sin 30°cos 45°=?×?-?×?=
?, 由?=?,
可得c=?=3(?-1)=3?-3.
思维突破
已知三角形的两角和任一边解三角形的基本思路:
①若所给边是已知角的对边,则先由正弦定理求另一角所对的边,再由三角形
的内角和定理求出第三个角,然后由正弦定理求第三个角所对的边.
②若所给边不是已知角的对边,则先由三角形的内角和定理求出第三个角,再
由正弦定理求另外两边.
跟踪训练
2-1 在△ABC中,a=1,A=?,B=?,则c=?( )
A.? ????B.?
C.? ????D.?
A
解析???C=π-?-?,
则sin C=sin?=sin?
=?×?+?×?=?.
由?=?,
得c=?=?=?,故选A.
探究三 利用正弦定理边角互化
例3 (1)(2020辽宁锦州高一下学期期末)在△ABC中,内角A、B、C所对的边
分别为a、b、c.若bcos C+ccos B=asin A,则角A的值为?( )
A.? ????B.?
C.? ????D.?
(2)若A,B是△ABC的内角,且sin A>sin B,则A与B的关系是?( )
A.AB C.A+B>? ????D.无法确定
C
B
解析 (1)由正弦定理得sin Bcos C+sin Ccos B=sin(B+C)=sin 2A.
∵A+B+C=π,
∴sin(B+C)=sin(π-A)=sin A,
∴sin A=sin2A.
∵A∈(0,π),∴sin A≠0,∴sin A=1,
∴A=?.故选C.
(2)?=?=2R,∴sin A>sin B??>??a>b?A>B,故选B.
思维突破
由?=?=?可得sin A∶sin B∶sin C=a∶b∶c,从而达到边角互化的目
的,解题时既可以将边化成角,利用三角恒等变换等知识求解,也可以将角化成
边,利用因式分解等知识求解.
跟踪训练
3-1 在△ABC中,角A,B,C的对边分别是a,b,c,且b=1,c=2,A=2B,则?等于?
( )
A.? ????B.3
C.? ????D.?
D
解析 因为A=2B,所以C=π-(A+B)=π-3B,所以sin C=sin 3B,
由正弦定理可得
?=?=?=?.故选D.
3-2????在△ABC中,已知c=2acos B,且A=45°,则角B的度数是( )
A.90° ????B.60°
C.45° ????D.40°
C
解析 ∵c=2acos B,∴sin C=2sin Acos B,
∴sin(A+B)=2sin Acos B,
∴sin Acos B+cos Asin B=2sin Acos B,∴sin(A-B)=0,
又-π∵A=45°,∴B=45°.故选C.
课堂检测
评价检测·素养提升
1.在△ABC中,AB=c,AC=b,BC=a,则下列等式中总能成立的是( )
A.asin A=bsin B
B.bsin C=csin A
C.absin C=bcsin B
D.asin C=csin A
D
解析 由?=?=?,得asin C=csin A.
2.在△ABC中,角A,B,C的对边分别为a,b,c,已知a=1,A=60°,C=30°,则c=?( )
A.? ????B.?
C.?或? ????D.?
A
解析 由?=?,得c=?=?.
3.在△ABC中,角A,B,C的对边分别为a,b,c,b=3,c=3,B=30°,则a的值为?( )
A.3 ????B.2?
C.3? ????D.2
解析 因为在△ABC中,b=3,c=3,B=30°,
所以C=B=30°,因此A=180°-C-B=120°,
由正弦定理可得?=?=?=6,
所以a=6sin A=6sin 120°=3?.故选C.
C
4.在△ABC中,角A、B、C的对边分别为a、b、c,已知2cos B=?,则此三角形为
?( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
B
解析 因为2cos B=?,
所以由正弦定理可得2cos B=?, 即2sin Ccos B=sin A,
因为sin A=sin(B+C),
所以2sin Ccos B=sin Bcos C+cos Bsin C,
因此sin Ccos B=sin Bcos C,故tan C=tan B,
所以B=C,即此三角形为等腰三角形.
由已知条件推不出△ABC是直角三角形.故选B.
5.已知在△ABC中,角A,B,C的对边分别为a,b,c,a=?,b=?,B=45°,解这个三角
形.
综上,A=60°,C=75°,c=?或A=120°,C=15°,c=?.
解析 由?=?,得sin A=?. ∵a>b,∴A>B=45°,∴A=60°或120°.
当A=60°时,C=180°-45°-60°=75°,
c=?=?=?=?;
当A=120°时,C=180°-45°-120°=15°, c=?=?
逻辑推理——利用正弦定理判断三角形形状
在△ABC中,若sin A=2sin Bcos C,且sin2A=sin2B+sin2C,试判断△ABC的形状.
解析 ∵sin2A=sin2B+sin2C,
∴a2=b2+c2,∴A是直角.
∵A=180°-(B+C),sin A=2sin Bcos C,
∴sin(B+C)=sin Bcos C+cos Bsin C=2sin Bcos C, ∴sin(B-C)=0.
又-90°∴△ABC是等腰直角三角形.
素养演练
素养探究:判断三角形形状的两种方法:
?
注意:1.在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因
式,以免漏解.
2.在解三角形中的边或角时,利用特殊三角形的性质,推出该三角形的具体形
状,解题过程中考查学生逻辑推理的核心素养.
针对训练
在△ABC中,cos2?=?(a、b、c分别为角A、B、C的对边),则△ABC为?
( )
A.等边三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
B
解析????cos2?=???=??cos Bsin C=sin A?cos Bsin C=
sin(B+C)?sin Bcos C=0?cos C=0?C=90°.由已知条件推不出△ABC是等腰三
角形.故选B.
§9.1 正弦定理与余弦定理
9.1.1 正弦定理
第一篇 教材过关
第1课时 正弦定理
情景导学
精读教材·必备知识
正弦定理是由伊朗著名的天文学家阿布尔·威发(940—998)首先发现与证明
的.中亚细亚人阿尔比鲁尼(973—1048)给三角形的正弦定理做出了一个证明.
也有说正弦定理的证明是13世纪的那希尔丁在《论完全四边形》中第一次把
三角学作为独立的学科进行论述,首次清楚地论证了正弦定理.至此三角学开
始脱离天文学,走上独立发展的道路.本节将学习三角学中的正弦定理.
1.正弦定理
在一个三角形中,各边的长和它所对角的正弦的比①______.
其公式为②??????.
教材研读
相等
提示?????=?=?=c.
思考1:如图,在Rt△ABC中,?,?,?各自等于什么?
?
2.正弦定理的常见变形
(1)sin A∶sin B∶sin C=③________;
(2)?=?=?=?=2R(R为△ABC外接圆半径);
(3)a=④______,b=⑤ ______,c=⑥ ______;
(4)sin A=⑦???,sin B=⑧????,sin C=⑨????.
a∶b∶c
2Rsin A
2Rsin B
2Rsin C
思考2:在△ABC中,已知acos B=bcos A.你能用角把等式中的边a,b表示出来吗?
提示 可借助正弦定理把边化成角:2Rsin Acos B=2Rsin Bcos A,移项后就是一个三角恒等变换公式sin Acos B-cos Asin B=0.
3.解三角形
习惯上,我们把三角形的?_____与?_____都称为三角形的元素,已知三角形
的若干元素求?________一般称为解三角形.
思考3:利用正弦定理可以解决哪两类有关三角形的问题?
3个角
3条边
其他元素
提示 ①已知两角和任意一边,求其他两边和第三个角;
②已知两边和其中一边的对角,求另一边的对角,从而求出其他的边和角.
互动探究·关键能力
探究一????已知两边及一边的对角解三角形
例1 (1)(易错题)(2019辽宁凌源二中期末)在△ABC中,若A=30°,BC=4,AC=4
?,则角B为?( )
A.45° ????B.45°或135°
C.60° ????D.135°
(2)设△ABC的内角A,B,C所对的边分别为a,b,c,若a=3,b=?,A=?,则B= ?(???? )
A.? ????B.? ????C.? ????D.?或?
B
B
解析 (1)在△ABC中,由正弦定理得?=?,∴sin B=?,∵BC
(1)由正弦值得出角的大小时注意判断所得出的角的大小是否满足条件,避免
漏解或多解.
(2)已知三角形的两边和其中一边的对角解三角形时的方法:
首先,由正弦定理求出另一边对角的正弦值.
其次,如果已知的角为大边所对的角,那么由三角形中“大边对大角,大角对大
边”能判断另一边所对的角为锐角,由正弦值可求唯一的锐角;如果已知的角
为小边所对的角,那么不能判断另一边所对的角是不是锐角,这时由正弦值可
求出两个角.
跟踪训练
1-1 在△ABC中,a=2,b=?,B=?,则sin A的值是?( )
A.? ????B.?
C.? ????D.?或?
B
解析 由正弦定理得?=?,∴sin A=?·sin ?=?,故选B.
1-2 设△ABC的内角A、B、C所对的边分别为a、b、c,若a=3,b=?,A=?,则
B=?( )
A.? ????B.?或?
C.? ????D.?或?
A
解析 由正弦定理得sin B=?
=?=?,
又b
探究二 已知两角及一边解三角形
例2 在△ABC中,角A,B,C的对边分别为a,b,c,A=45°,B=120°,a=6,则b=?( )
A.2? ????B.3? ????C.3? ????D.3?
D
解析 ∵?=?,∴b=?=?=3?.故选D.
变式训练
(变结论)若例2中的条件不变,求c的值.
解析 ∵A=45°,B=120°, ∴C=15°.
∴sin C=sin 15°=sin(45°-30°)=sin 45°·cos 30°-sin 30°cos 45°=?×?-?×?=
?, 由?=?,
可得c=?=3(?-1)=3?-3.
思维突破
已知三角形的两角和任一边解三角形的基本思路:
①若所给边是已知角的对边,则先由正弦定理求另一角所对的边,再由三角形
的内角和定理求出第三个角,然后由正弦定理求第三个角所对的边.
②若所给边不是已知角的对边,则先由三角形的内角和定理求出第三个角,再
由正弦定理求另外两边.
跟踪训练
2-1 在△ABC中,a=1,A=?,B=?,则c=?( )
A.? ????B.?
C.? ????D.?
A
解析???C=π-?-?,
则sin C=sin?=sin?
=?×?+?×?=?.
由?=?,
得c=?=?=?,故选A.
探究三 利用正弦定理边角互化
例3 (1)(2020辽宁锦州高一下学期期末)在△ABC中,内角A、B、C所对的边
分别为a、b、c.若bcos C+ccos B=asin A,则角A的值为?( )
A.? ????B.?
C.? ????D.?
(2)若A,B是△ABC的内角,且sin A>sin B,则A与B的关系是?( )
A.A
C
B
解析 (1)由正弦定理得sin Bcos C+sin Ccos B=sin(B+C)=sin 2A.
∵A+B+C=π,
∴sin(B+C)=sin(π-A)=sin A,
∴sin A=sin2A.
∵A∈(0,π),∴sin A≠0,∴sin A=1,
∴A=?.故选C.
(2)?=?=2R,∴sin A>sin B??>??a>b?A>B,故选B.
思维突破
由?=?=?可得sin A∶sin B∶sin C=a∶b∶c,从而达到边角互化的目
的,解题时既可以将边化成角,利用三角恒等变换等知识求解,也可以将角化成
边,利用因式分解等知识求解.
跟踪训练
3-1 在△ABC中,角A,B,C的对边分别是a,b,c,且b=1,c=2,A=2B,则?等于?
( )
A.? ????B.3
C.? ????D.?
D
解析 因为A=2B,所以C=π-(A+B)=π-3B,所以sin C=sin 3B,
由正弦定理可得
?=?=?=?.故选D.
3-2????在△ABC中,已知c=2acos B,且A=45°,则角B的度数是( )
A.90° ????B.60°
C.45° ????D.40°
C
解析 ∵c=2acos B,∴sin C=2sin Acos B,
∴sin(A+B)=2sin Acos B,
∴sin Acos B+cos Asin B=2sin Acos B,∴sin(A-B)=0,
又-π
课堂检测
评价检测·素养提升
1.在△ABC中,AB=c,AC=b,BC=a,则下列等式中总能成立的是( )
A.asin A=bsin B
B.bsin C=csin A
C.absin C=bcsin B
D.asin C=csin A
D
解析 由?=?=?,得asin C=csin A.
2.在△ABC中,角A,B,C的对边分别为a,b,c,已知a=1,A=60°,C=30°,则c=?( )
A.? ????B.?
C.?或? ????D.?
A
解析 由?=?,得c=?=?.
3.在△ABC中,角A,B,C的对边分别为a,b,c,b=3,c=3,B=30°,则a的值为?( )
A.3 ????B.2?
C.3? ????D.2
解析 因为在△ABC中,b=3,c=3,B=30°,
所以C=B=30°,因此A=180°-C-B=120°,
由正弦定理可得?=?=?=6,
所以a=6sin A=6sin 120°=3?.故选C.
C
4.在△ABC中,角A、B、C的对边分别为a、b、c,已知2cos B=?,则此三角形为
?( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
B
解析 因为2cos B=?,
所以由正弦定理可得2cos B=?, 即2sin Ccos B=sin A,
因为sin A=sin(B+C),
所以2sin Ccos B=sin Bcos C+cos Bsin C,
因此sin Ccos B=sin Bcos C,故tan C=tan B,
所以B=C,即此三角形为等腰三角形.
由已知条件推不出△ABC是直角三角形.故选B.
5.已知在△ABC中,角A,B,C的对边分别为a,b,c,a=?,b=?,B=45°,解这个三角
形.
综上,A=60°,C=75°,c=?或A=120°,C=15°,c=?.
解析 由?=?,得sin A=?. ∵a>b,∴A>B=45°,∴A=60°或120°.
当A=60°时,C=180°-45°-60°=75°,
c=?=?=?=?;
当A=120°时,C=180°-45°-120°=15°, c=?=?
逻辑推理——利用正弦定理判断三角形形状
在△ABC中,若sin A=2sin Bcos C,且sin2A=sin2B+sin2C,试判断△ABC的形状.
解析 ∵sin2A=sin2B+sin2C,
∴a2=b2+c2,∴A是直角.
∵A=180°-(B+C),sin A=2sin Bcos C,
∴sin(B+C)=sin Bcos C+cos Bsin C=2sin Bcos C, ∴sin(B-C)=0.
又-90°
素养演练
素养探究:判断三角形形状的两种方法:
?
注意:1.在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因
式,以免漏解.
2.在解三角形中的边或角时,利用特殊三角形的性质,推出该三角形的具体形
状,解题过程中考查学生逻辑推理的核心素养.
针对训练
在△ABC中,cos2?=?(a、b、c分别为角A、B、C的对边),则△ABC为?
( )
A.等边三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
B
解析????cos2?=???=??cos Bsin C=sin A?cos Bsin C=
sin(B+C)?sin Bcos C=0?cos C=0?C=90°.由已知条件推不出△ABC是等腰三
角形.故选B.
