1.3.3 非(not)(共18张PPT) 数学人教A版选修1-1
文档属性
| 名称 | 1.3.3 非(not)(共18张PPT) 数学人教A版选修1-1 |

|
|
| 格式 | pptx | ||
| 文件大小 | 498.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 10:20:47 | ||
图片预览






文档简介
1.3简单的逻辑联结词
1.3.3 非
p
q
p∨q
真
真
真
假
假
真
假
假
p
q
p∧q
真
真
真
假
假
真
假
假
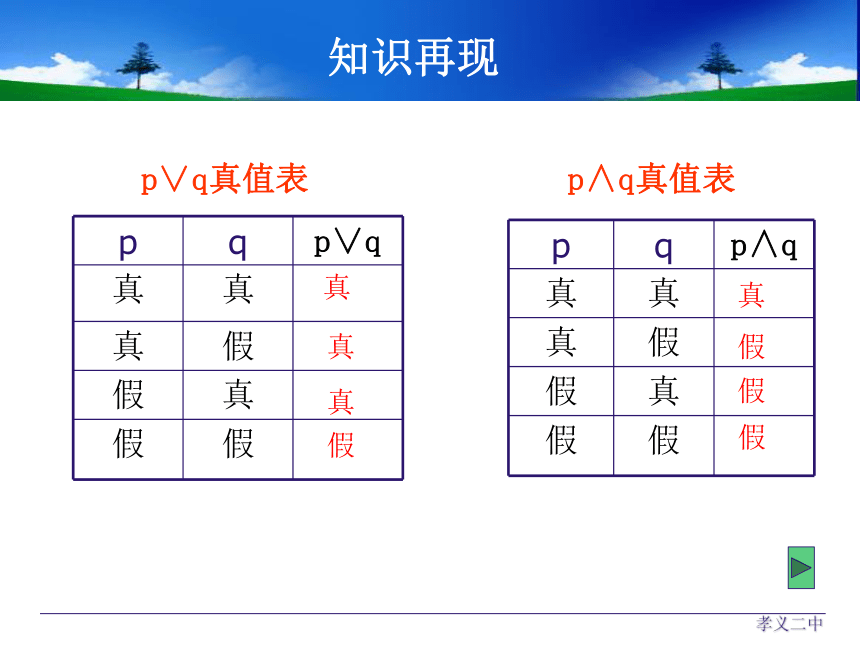
p∨q真值表
p∧q真值表
真
真
真
假
真
假
假
假
孝义二中
知识再现
引入 歌德是18世纪德国的一位著名文艺大师,一天,他与一位文艺批评家“狭路相逢”.这位批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,一边高傲地往前走,一边大声说道:“我从来不给傻子让路!”面对如此尴尬局面,但见歌德笑容可掬,谦恭地闪在一旁,一边有礼貌地回答道:“呵呵,我可恰恰相反.”结果故作聪明的批评家,反倒自讨个没趣.
从逻辑角度分析,歌德回答的意思是什么?
孝义二中
孝义二中
思考1
下列两组命题间有什么关系?
1.(1)35能被5整除;
(2)35不能被5整除.
2.(1)方程 x2+x+1=0有实数根;
(2)方程 x2+x+1=0无实数根.
命题(2)是命题(1)的否定,“非”表示“否定”“不是”“问题的反面”
一般地,对一个命题p全盘否定,就得到一个新命题,记作: ? p,读作"非p"或者“p的否定”
孝义二中
填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考2 命题P与┐p的真假关系如何?
一句话概括:
真假相反
p与┐p真假性相反
真命题
假命题
p
? p
真
假
假
真
孝义二中
例1:写出下列命题的否定,并判断它们的真假:
(1)p: 是周期函数;
(2)p: ;
(3)p:空集是集合A的子集.
解:(1)﹁p: 不是周期函数.
∵ p是真命题, ∴ ﹁p是假命题.
(2)﹁p: ;
∵p是假命题, ∴ ﹁p是真命题.
(3)﹁p:空集不是集合A的子集.
∵ p是真命题, ∴ ﹁p是假命题.
例题分析
孝义二中
练习1 写出下列命题的否定并判断他们的真假:
(1)2+2=5;
┓p:
(2)3是方程 的根;
┓p:
反思:┓p的真假性的判断,关键在于p的真假的判断。 有时如果P的真假不好判断,可以判断┓p的真假
2+2 ≠5
3不是方程 的根
真命题
假命题
假
真
孝义二中
对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP.
探究1:逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?
活动探究
孝义二中
例2:写出命题p: “正方形的四条边相等”的否定与它的否命题.
命题┓p:
P的否命题:
正方形的四条边不相等.
若一个四边形不是正方形,则它的四条边不相等.
探究2:命题的否定与否命题是不是同一概念呢?他们具有怎样的区别呢?
命题的否定与否命题是完全不同的概念
孝义二中
2.原命题: 若 p , 则 q .
命题的否定: 若 p ,则┐q .
否命题: 若 ┐p , 则┐q .
3.命题的否定(非)的真假性与原命题相反;而否命题的真假性与原命题无关.
1. 否命题:条件和结论都否定
命题的否定:只否定结论,不否定条件
命题的否定和否命题的区别
孝义二中
.
常见词语的否定形式:
正面
词语
等于
(=)
大于
(>)
小于
(<)
能
是
都(全)
是
任意
的
任意
两个
所
有
否定
词语
不等于
不大于
不小于
不能
不是
不都
(全)是
某个
某两个
某些
( )
≠
( )
≤
( )
≥
正面
词语
至多
一个
至少有一个
至多
n个
p或q
p且q
否定
词语
非p且非q
非p或非q
至少
两个
一个也没有
至少有(n+1)个
练习2 写出下列各命题的否定及其否命题,并判断它 们的真假.
(1)若x、y都是奇数,则x+y是偶数
(2)若x2-3x-10=0,则x=-2或x=5.
命题的否定:若x、y都是奇数,则x+y不是偶数,假
命题的否命题:若x,y不都是奇数,则x+y不是偶数,假.
.
命题的否定:若x2-3x-10=0,则x≠-2且x≠5,假
命题的否命题:若x2-3x-10≠0,则x≠-2且x≠5,真
1.若命题“﹁p”与命题“p∨q”都是真
命题,那么( )
A.命题p与命题q的真假相同
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p不一定是真命题
B
当堂练习:
孝义二中
2.a≥5且b≥2的否定是_____________.
a<5或b<2
3.(2015·杭州高二检测)已知p:2+2=5,q:3>2,则下列判断正确的是 ( )
A.“p∨q”为假,“﹁q”为假
B.“p∨q”为真,“﹁q”为假
C.“p∧q”为真,“﹁p”为假
D.“p∧q”为真,“p∨q”为假
B
【延伸探究】本例条件不变,试判断命题:(﹁p)∧q,p∧(﹁q),
(﹁p)∧(﹁q)的真假.
【解析】由条件知,p假,q真,所以﹁p真,﹁q为假,故(﹁p)∧q为真,p∧(﹁q)为假,(﹁p)∧(﹁q)为假.
孝义二中
命题p:x2-3x-4>0,命题q:
若q∧(﹁p)为真,求x的取值范围.
能力提升
孝义二中
【解析】若p真,则x2-3x-4>0?x>4或x<-1,
若q真,则 ?2≤x<3.
因为q∧(﹁p)为真,则命题q与﹁p均为真命题,
故p假q真,所以 解得2≤x<3.
所以x的取值范围是[2,3).
1.非的含义及真假性判断
2.命题的否定和否命题之间的区别
3.非与集合中某些概念的联系
1.知识点:
2.思想方法:
小结
联系的思想、由特殊到一般的思想
孝义二中
课后作业
1.教材P18习题1.3A组第3题,教材P30复习参考题A组第6题
2.预习全称量词
孝义二中
孝义二中
www.themegallery.com
再见
孝义二中
1.3.3 非
p
q
p∨q
真
真
真
假
假
真
假
假
p
q
p∧q
真
真
真
假
假
真
假
假
p∨q真值表
p∧q真值表
真
真
真
假
真
假
假
假
孝义二中
知识再现
引入 歌德是18世纪德国的一位著名文艺大师,一天,他与一位文艺批评家“狭路相逢”.这位批评家生性古怪,遇到歌德走来,不仅没有相让,反而卖弄聪明,一边高傲地往前走,一边大声说道:“我从来不给傻子让路!”面对如此尴尬局面,但见歌德笑容可掬,谦恭地闪在一旁,一边有礼貌地回答道:“呵呵,我可恰恰相反.”结果故作聪明的批评家,反倒自讨个没趣.
从逻辑角度分析,歌德回答的意思是什么?
孝义二中
孝义二中
思考1
下列两组命题间有什么关系?
1.(1)35能被5整除;
(2)35不能被5整除.
2.(1)方程 x2+x+1=0有实数根;
(2)方程 x2+x+1=0无实数根.
命题(2)是命题(1)的否定,“非”表示“否定”“不是”“问题的反面”
一般地,对一个命题p全盘否定,就得到一个新命题,记作: ? p,读作"非p"或者“p的否定”
孝义二中
填空:当p为真命题时,则┐p为 ;当p为假命题时,则┐p为 .
思考2 命题P与┐p的真假关系如何?
一句话概括:
真假相反
p与┐p真假性相反
真命题
假命题
p
? p
真
假
假
真
孝义二中
例1:写出下列命题的否定,并判断它们的真假:
(1)p: 是周期函数;
(2)p: ;
(3)p:空集是集合A的子集.
解:(1)﹁p: 不是周期函数.
∵ p是真命题, ∴ ﹁p是假命题.
(2)﹁p: ;
∵p是假命题, ∴ ﹁p是真命题.
(3)﹁p:空集不是集合A的子集.
∵ p是真命题, ∴ ﹁p是假命题.
例题分析
孝义二中
练习1 写出下列命题的否定并判断他们的真假:
(1)2+2=5;
┓p:
(2)3是方程 的根;
┓p:
反思:┓p的真假性的判断,关键在于p的真假的判断。 有时如果P的真假不好判断,可以判断┓p的真假
2+2 ≠5
3不是方程 的根
真命题
假命题
假
真
孝义二中
对“非”的理解,可联想到集合中的“补集”概念,若命题p对应于集合P,则命题非p就对应着集合P在全集U中的补集CUP.
探究1:逻辑联结词“非”的含义与集合中学过的哪个概念的意义相同呢?
活动探究
孝义二中
例2:写出命题p: “正方形的四条边相等”的否定与它的否命题.
命题┓p:
P的否命题:
正方形的四条边不相等.
若一个四边形不是正方形,则它的四条边不相等.
探究2:命题的否定与否命题是不是同一概念呢?他们具有怎样的区别呢?
命题的否定与否命题是完全不同的概念
孝义二中
2.原命题: 若 p , 则 q .
命题的否定: 若 p ,则┐q .
否命题: 若 ┐p , 则┐q .
3.命题的否定(非)的真假性与原命题相反;而否命题的真假性与原命题无关.
1. 否命题:条件和结论都否定
命题的否定:只否定结论,不否定条件
命题的否定和否命题的区别
孝义二中
.
常见词语的否定形式:
正面
词语
等于
(=)
大于
(>)
小于
(<)
能
是
都(全)
是
任意
的
任意
两个
所
有
否定
词语
不等于
不大于
不小于
不能
不是
不都
(全)是
某个
某两个
某些
( )
≠
( )
≤
( )
≥
正面
词语
至多
一个
至少有一个
至多
n个
p或q
p且q
否定
词语
非p且非q
非p或非q
至少
两个
一个也没有
至少有(n+1)个
练习2 写出下列各命题的否定及其否命题,并判断它 们的真假.
(1)若x、y都是奇数,则x+y是偶数
(2)若x2-3x-10=0,则x=-2或x=5.
命题的否定:若x、y都是奇数,则x+y不是偶数,假
命题的否命题:若x,y不都是奇数,则x+y不是偶数,假.
.
命题的否定:若x2-3x-10=0,则x≠-2且x≠5,假
命题的否命题:若x2-3x-10≠0,则x≠-2且x≠5,真
1.若命题“﹁p”与命题“p∨q”都是真
命题,那么( )
A.命题p与命题q的真假相同
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p不一定是真命题
B
当堂练习:
孝义二中
2.a≥5且b≥2的否定是_____________.
a<5或b<2
3.(2015·杭州高二检测)已知p:2+2=5,q:3>2,则下列判断正确的是 ( )
A.“p∨q”为假,“﹁q”为假
B.“p∨q”为真,“﹁q”为假
C.“p∧q”为真,“﹁p”为假
D.“p∧q”为真,“p∨q”为假
B
【延伸探究】本例条件不变,试判断命题:(﹁p)∧q,p∧(﹁q),
(﹁p)∧(﹁q)的真假.
【解析】由条件知,p假,q真,所以﹁p真,﹁q为假,故(﹁p)∧q为真,p∧(﹁q)为假,(﹁p)∧(﹁q)为假.
孝义二中
命题p:x2-3x-4>0,命题q:
若q∧(﹁p)为真,求x的取值范围.
能力提升
孝义二中
【解析】若p真,则x2-3x-4>0?x>4或x<-1,
若q真,则 ?2≤x<3.
因为q∧(﹁p)为真,则命题q与﹁p均为真命题,
故p假q真,所以 解得2≤x<3.
所以x的取值范围是[2,3).
1.非的含义及真假性判断
2.命题的否定和否命题之间的区别
3.非与集合中某些概念的联系
1.知识点:
2.思想方法:
小结
联系的思想、由特殊到一般的思想
孝义二中
课后作业
1.教材P18习题1.3A组第3题,教材P30复习参考题A组第6题
2.预习全称量词
孝义二中
孝义二中
www.themegallery.com
再见
孝义二中
