1.2.2 同角三角函数的基本关系课件(共15张PPT) 数学人教A版必修4
文档属性
| 名称 | 1.2.2 同角三角函数的基本关系课件(共15张PPT) 数学人教A版必修4 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 10:29:43 | ||
图片预览






文档简介
同角三角函数的基本关式
角? 的终边上的任意一点P(x,y),点 P 到原点的
距离为 r,
任意角三角函数定义:
=????????
?
????=????????=
?
????2+????2
?
角? 的余弦. cos ?
角? 的正弦. sin ?
=????????
?
角? 的正切. tan ?
=????????
?
角 ? 终边
x
y
P(x,y)
O
r
复习
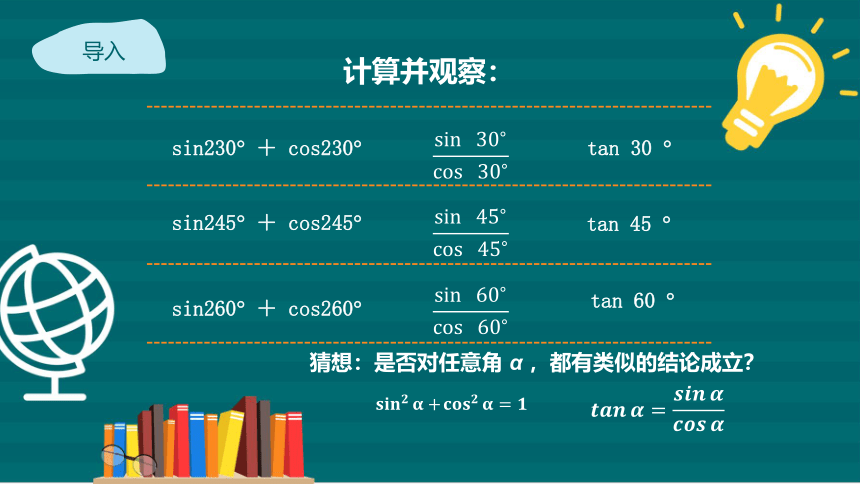
sin?30?cos?30?
?
tan 30 ?
tan 45 ?
sin?45?cos?45?
?
sin?60?cos?60?
?
tan 60 ?
????????????????????+????????????????????=????
?
????????????????=????????????????????????????????
?
猜想:是否对任意角 α ,都有类似的结论成立?
计算并观察:
导入
sin230? + cos230?
sin260? + cos260?
sin245? + cos245?
根据三角函数定义证明:
sin2 ? + cos2 ? =1,tan ? =
sin?????cos?????
?
证明:
角? 的终边上的任意一点P(x,y),点 P 到
原点的距离为 ,
r=OP=x2+y2
?
证明
sin2 ? + cos2 ?
=
????????2+????????2=
?
????2????2+????2????2=
?
????2+????2????2=
?
1
?
sin?????cos?????=
?
????????×????????=
?
????????
?
1、同角三角函数的基本关系式
商数关系
“同角”二层含义: 一是角相同;二是“任意”一个角.
试一试(填空):
平方关系
知识点
tan????=sin????cos????
?
sin2????+cos2????=1
?
(1)sin221? + ________ =1 ;(2)________ + cos2 ? =1
(3)tan 39? = (4) tan ?=
cos39?
?
判断下列式子是否正确?
√
√
×
√
×
2、如何理解“同角”?
1、sin243°+cos2?43°=1
?
4、sin2αcos2α=2tanα
?
3、sin2β2+cos2?β2=1
?
2、sin2π5+cos2?π6=1
?
5、sin(2α?β)cos(2α?β) = tan((2α?β)
?
“同角”二层含义:
一是“角相同”,
二是对“任意”一个角(在使得函数有意义的前提下) 关系式都成立
思考1:对于平方关系
思考2:对于商数关系
3.探究
可作哪些变形?
????????????????????+????????????????????=????
?
????????????????????=?????????????????????????
?
????????????????????=1- ????????????????????
?
(?????????????????+?????????????????)????=1+2 sin ??????????????????????
?
(???????????????????????????????????)????=1-2 sin ??????????????????????
?
sin ????=?????????????????·?tan ????
?
????????????????????????????????=????????????????
?
????????????????= ????????????????????????????????
?
可作哪些变形?
tan????=sin????cos????=
?
45?35=?
?
?43
?
4.例题讲解
求正切.
求余弦
已知正弦
小结步骤:
平 方 关 系
商 数 关 系
例1 已知 ,且 ? 是第二象限的角, 求 角 ? 的余弦和正切值.
sin????=45
?
解 由 sin2 ? + cos2 ? =1,得
cos????=±1?sin2????
?
cos????<0?,
?
因为
cos????=?1?452=?35
?
所以
? 是第二象限角,
一、根据下列条件,求角??????的另外2个三角函数值.
?
1、 ,
????????????????=????????
?
2、 ,
????????????????=?????????
?
3、 ,
????????????????=????????
?
4、 ,
????????????????=?????????
?
5.巩固练习1
且????是第三象限的角;
?
且????是第四象限的角;
?
且????是第三象限的角;
?
且??????是第一象限的角;
?
解:
∴cos????=?925=?35
?
tan????=sin????cos????=45×53=43
?
∴cos????=925=35
?
tan????=sin????cos????=45×(?53)=?43
?
由sin2????+cos2????=1得
?
cos????=±1?sin2????=±35
?
当
cos????>0
?
是第一象限角时
当
cos????<0
?
是第一象限角时
自我反思:
解:由????????????????=45得????????????????=±1?????????????2????=±35得????????????????=±????????????????????????????????=±43
?
所得结果的符号由角所在象限决定
?
变式1、已知sin????=45,求cos????,tan????的值
?
????当 是第一象限角时,
?
cos????>0
?
∴角????是第一或第二象限角
?
变式2、已知tan????=?3,求sin????,cos????的值
?
∵tan????<0∴????为第二或第四象限角
?
∴{sin2????+cos2????=1sin????cos????=?3
?
解得:{cos2????=14sin2????=34
?
sin2????+cos2????=1
?
sin????cos????=tan????
?
方程(组)思想
解:
∵tan????=sin????cos????
?
当????为第四象限角时sin????=?34=?32,cos????=14=12
?
当????为第二象限角时sin????=34=32,cos????=?14=?12
?
6.当堂检测
已知??????????????????=?????????????,则sin ???? 的值为
?
自主解答∵????????????????=?????????????,
?
即?????????????????????????????????????????????= ???????????????????? ,
?
∵????????????????????????????????????????= ????????????????????
?
解得 sin???????=±????????????????
?
7.归纳小结
数学
同角三角函数的基本关系式
知识与题型:
同角三角函数基本关系式
求值
解决
同角三角函数的基本关系式及其变形,
求值题目的思路与注意事项.
01
02
1、 教材P20,练习第 1,2题;
2、教材P21 ,第10,11,12题
8.课后作业
感谢您的观看
角? 的终边上的任意一点P(x,y),点 P 到原点的
距离为 r,
任意角三角函数定义:
=????????
?
????=????????=
?
????2+????2
?
角? 的余弦. cos ?
角? 的正弦. sin ?
=????????
?
角? 的正切. tan ?
=????????
?
角 ? 终边
x
y
P(x,y)
O
r
复习
sin?30?cos?30?
?
tan 30 ?
tan 45 ?
sin?45?cos?45?
?
sin?60?cos?60?
?
tan 60 ?
????????????????????+????????????????????=????
?
????????????????=????????????????????????????????
?
猜想:是否对任意角 α ,都有类似的结论成立?
计算并观察:
导入
sin230? + cos230?
sin260? + cos260?
sin245? + cos245?
根据三角函数定义证明:
sin2 ? + cos2 ? =1,tan ? =
sin?????cos?????
?
证明:
角? 的终边上的任意一点P(x,y),点 P 到
原点的距离为 ,
r=OP=x2+y2
?
证明
sin2 ? + cos2 ?
=
????????2+????????2=
?
????2????2+????2????2=
?
????2+????2????2=
?
1
?
sin?????cos?????=
?
????????×????????=
?
????????
?
1、同角三角函数的基本关系式
商数关系
“同角”二层含义: 一是角相同;二是“任意”一个角.
试一试(填空):
平方关系
知识点
tan????=sin????cos????
?
sin2????+cos2????=1
?
(1)sin221? + ________ =1 ;(2)________ + cos2 ? =1
(3)tan 39? = (4) tan ?=
cos39?
?
判断下列式子是否正确?
√
√
×
√
×
2、如何理解“同角”?
1、sin243°+cos2?43°=1
?
4、sin2αcos2α=2tanα
?
3、sin2β2+cos2?β2=1
?
2、sin2π5+cos2?π6=1
?
5、sin(2α?β)cos(2α?β) = tan((2α?β)
?
“同角”二层含义:
一是“角相同”,
二是对“任意”一个角(在使得函数有意义的前提下) 关系式都成立
思考1:对于平方关系
思考2:对于商数关系
3.探究
可作哪些变形?
????????????????????+????????????????????=????
?
????????????????????=?????????????????????????
?
????????????????????=1- ????????????????????
?
(?????????????????+?????????????????)????=1+2 sin ??????????????????????
?
(???????????????????????????????????)????=1-2 sin ??????????????????????
?
sin ????=?????????????????·?tan ????
?
????????????????????????????????=????????????????
?
????????????????= ????????????????????????????????
?
可作哪些变形?
tan????=sin????cos????=
?
45?35=?
?
?43
?
4.例题讲解
求正切.
求余弦
已知正弦
小结步骤:
平 方 关 系
商 数 关 系
例1 已知 ,且 ? 是第二象限的角, 求 角 ? 的余弦和正切值.
sin????=45
?
解 由 sin2 ? + cos2 ? =1,得
cos????=±1?sin2????
?
cos????<0?,
?
因为
cos????=?1?452=?35
?
所以
? 是第二象限角,
一、根据下列条件,求角??????的另外2个三角函数值.
?
1、 ,
????????????????=????????
?
2、 ,
????????????????=?????????
?
3、 ,
????????????????=????????
?
4、 ,
????????????????=?????????
?
5.巩固练习1
且????是第三象限的角;
?
且????是第四象限的角;
?
且????是第三象限的角;
?
且??????是第一象限的角;
?
解:
∴cos????=?925=?35
?
tan????=sin????cos????=45×53=43
?
∴cos????=925=35
?
tan????=sin????cos????=45×(?53)=?43
?
由sin2????+cos2????=1得
?
cos????=±1?sin2????=±35
?
当
cos????>0
?
是第一象限角时
当
cos????<0
?
是第一象限角时
自我反思:
解:由????????????????=45得????????????????=±1?????????????2????=±35得????????????????=±????????????????????????????????=±43
?
所得结果的符号由角所在象限决定
?
变式1、已知sin????=45,求cos????,tan????的值
?
????当 是第一象限角时,
?
cos????>0
?
∴角????是第一或第二象限角
?
变式2、已知tan????=?3,求sin????,cos????的值
?
∵tan????<0∴????为第二或第四象限角
?
∴{sin2????+cos2????=1sin????cos????=?3
?
解得:{cos2????=14sin2????=34
?
sin2????+cos2????=1
?
sin????cos????=tan????
?
方程(组)思想
解:
∵tan????=sin????cos????
?
当????为第四象限角时sin????=?34=?32,cos????=14=12
?
当????为第二象限角时sin????=34=32,cos????=?14=?12
?
6.当堂检测
已知??????????????????=?????????????,则sin ???? 的值为
?
自主解答∵????????????????=?????????????,
?
即?????????????????????????????????????????????= ???????????????????? ,
?
∵????????????????????????????????????????= ????????????????????
?
解得 sin???????=±????????????????
?
7.归纳小结
数学
同角三角函数的基本关系式
知识与题型:
同角三角函数基本关系式
求值
解决
同角三角函数的基本关系式及其变形,
求值题目的思路与注意事项.
01
02
1、 教材P20,练习第 1,2题;
2、教材P21 ,第10,11,12题
8.课后作业
感谢您的观看
