3.3.2 简单的线性规划问题课件(共15张PPT) 数学人教A版必修5
文档属性
| 名称 | 3.3.2 简单的线性规划问题课件(共15张PPT) 数学人教A版必修5 |  | |
| 格式 | ppt | ||
| 文件大小 | 776.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 22:09:38 | ||
图片预览






文档简介
(共15张PPT)
简单的线性规划问题
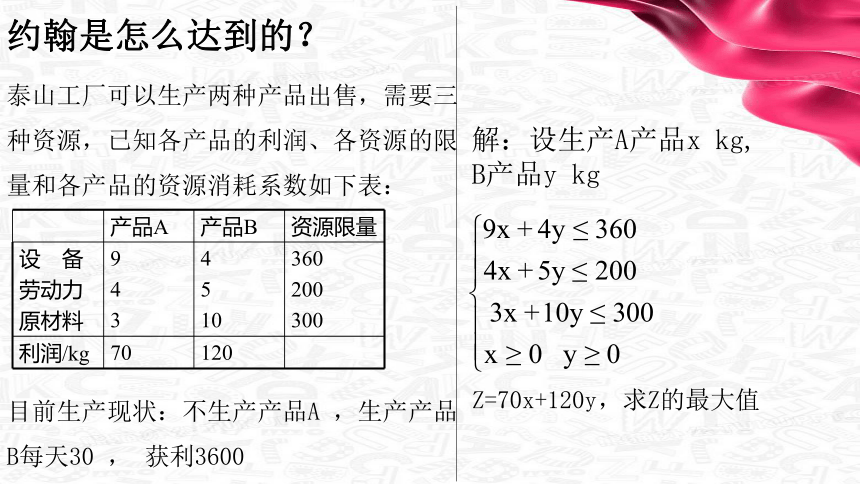
泰山工厂可以生产两种产品出售,需要三种资源,已知各产品的利润、各资源的限量和各产品的资源消耗系数如下表:
目前生产现状:
不生产产品A
,生产产品B每天30
,
获利3600
产品A
产品B
资源限量
设
备
劳动力
原材料
9
4
3
4
5
10
360
200
300
利润/kg
70
120
约翰成功应聘泰山工厂总经理!
在现有资源状况下,我可以使利润达到4280
!
1、求线性目标函数的最值
解:设生产A产品x
kg,
B产品y
kg
约翰是怎么达到的?
Z=70x+120y,求Z的最大值
产品A
产品B
资源限量
设
备
劳动力
原材料
9
4
3
4
5
10
360
200
300
利润/kg
70
120
泰山工厂可以生产两种产品出售,需要三种资源,已知各产品的利润、各资源的限量和各产品的资源消耗系数如下表:
目前生产现状:不生产产品A
,生产产品B每天30
,
获利3600
90
80
60
40
20
x
y
A
B
C
D
E
F
G
I
z=70x+120y
约翰是怎么达到的?
y
3x+10y
≤300
4x+5y≤200
0
20
40
60
80
100
F
y
9x+4y
≤
360
z=70x+120y变形为
是这条直线在y轴的截距,
最大时,z最大
令z=0,画出
的图,
是由
平移得到的
如图,过点I(20,24)时,
=4280
2、求非线性目标函数的最值
课堂巩固
课堂巩固
1、目标函数是线性目标函数时,z的几何意义与纵截距有关
2、目标函数是非线性目标函数时,常考虑目标函数的几何意义
(1)
表示点(x,y)与点(a,b)连线的斜率.
(2)
表示点(x,y)与点(a,b)间的距离;
课堂小结
作业布置
作业手册63页
必做题1--8,11
选做题9,10,12
作业布置
结束语
数学就在身边,我们需用心发现,用心感受,就想我能感受到你的感受一样。
简单的线性规划问题
泰山工厂可以生产两种产品出售,需要三种资源,已知各产品的利润、各资源的限量和各产品的资源消耗系数如下表:
目前生产现状:
不生产产品A
,生产产品B每天30
,
获利3600
产品A
产品B
资源限量
设
备
劳动力
原材料
9
4
3
4
5
10
360
200
300
利润/kg
70
120
约翰成功应聘泰山工厂总经理!
在现有资源状况下,我可以使利润达到4280
!
1、求线性目标函数的最值
解:设生产A产品x
kg,
B产品y
kg
约翰是怎么达到的?
Z=70x+120y,求Z的最大值
产品A
产品B
资源限量
设
备
劳动力
原材料
9
4
3
4
5
10
360
200
300
利润/kg
70
120
泰山工厂可以生产两种产品出售,需要三种资源,已知各产品的利润、各资源的限量和各产品的资源消耗系数如下表:
目前生产现状:不生产产品A
,生产产品B每天30
,
获利3600
90
80
60
40
20
x
y
A
B
C
D
E
F
G
I
z=70x+120y
约翰是怎么达到的?
y
3x+10y
≤300
4x+5y≤200
0
20
40
60
80
100
F
y
9x+4y
≤
360
z=70x+120y变形为
是这条直线在y轴的截距,
最大时,z最大
令z=0,画出
的图,
是由
平移得到的
如图,过点I(20,24)时,
=4280
2、求非线性目标函数的最值
课堂巩固
课堂巩固
1、目标函数是线性目标函数时,z的几何意义与纵截距有关
2、目标函数是非线性目标函数时,常考虑目标函数的几何意义
(1)
表示点(x,y)与点(a,b)连线的斜率.
(2)
表示点(x,y)与点(a,b)间的距离;
课堂小结
作业布置
作业手册63页
必做题1--8,11
选做题9,10,12
作业布置
结束语
数学就在身边,我们需用心发现,用心感受,就想我能感受到你的感受一样。
