1.1.2空间向量课件(共15张PPT) 数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.1.2空间向量课件(共15张PPT) 数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 22:14:11 | ||
图片预览




文档简介
(共15张PPT)
1.1.3空间向量的数量积运算
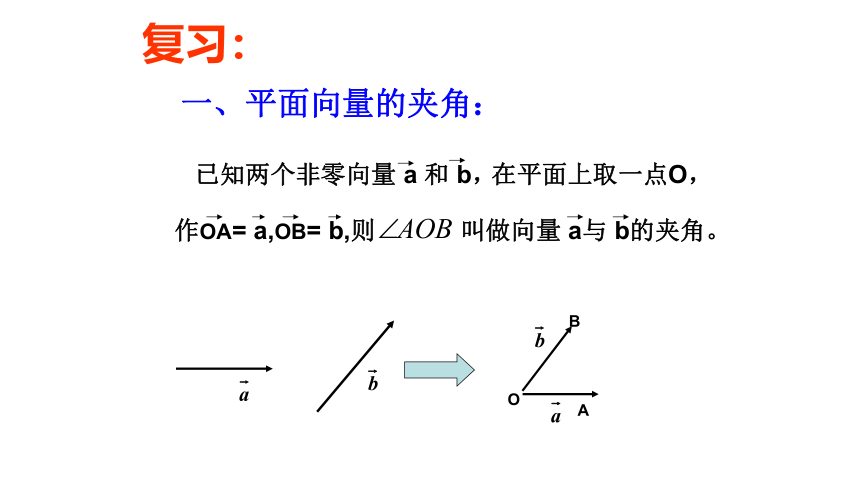
复习:
一、平面向量的夹角:
叫做向量
a与
b的夹角。
已知两个非零向量
a
和
b,
在平面上取一点O,
作OA=
a,OB=
b,则
A
O
B
二、平面向量的数量积的定义:
已知两个非零向量a,
b,则|a|
|b|cos
叫做向量a,
b的数量积,记作
即
并规定
0
1)空间向量的夹角的定义:
O
A
B
讲授新课:
异面直线及所成的角的范围?
2)空间向量的数量积
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积等于零.
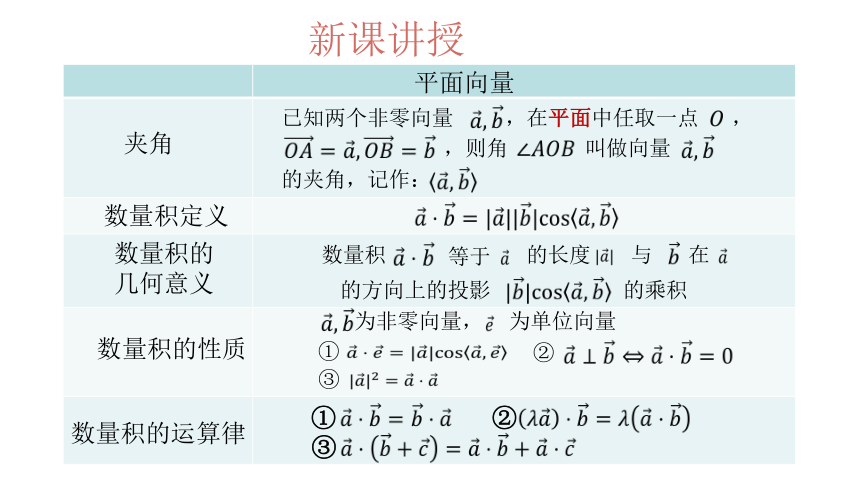
新课讲授
平面向量
夹角
数量积定义
数量积的
几何意义
数量积的性质
数量积的运算律
数量积
等于
的长度
与
在
的方向上的投影
的乘积
为非零向量,
为单位向量
①
②
③
已知两个非零向量
,在平面中任取一点
,
,则角
叫做向量
的夹角,记作:
①
②
③
新课讲授
空间向量
夹角
数量积定义
数量积的
几何意义
数量积的性质
数量积的运算律
数量积
等于
的长度
与
在
的方向上的投影
的乘积
为非零向量,
为单位向量
①
②
③
已知两个非零向量
,在空间中任取一点
,
,则角
叫做向量
的夹角,记作:
①
②
③
例1
C
例1
例2
例1
A
B
C
D
E
F
G
例2
互动探究2
求异面直线AB和CD所成的角.
例3
小结:
①
②
也有下列两个重要性质
作业:
课本P105
习题3.1
2
学案P48
例3
1.1.3空间向量的数量积运算
复习:
一、平面向量的夹角:
叫做向量
a与
b的夹角。
已知两个非零向量
a
和
b,
在平面上取一点O,
作OA=
a,OB=
b,则
A
O
B
二、平面向量的数量积的定义:
已知两个非零向量a,
b,则|a|
|b|cos
叫做向量a,
b的数量积,记作
即
并规定
0
1)空间向量的夹角的定义:
O
A
B
讲授新课:
异面直线及所成的角的范围?
2)空间向量的数量积
注:①两个向量的数量积是数量,而不是向量.
②规定:零向量与任意向量的数量积等于零.
新课讲授
平面向量
夹角
数量积定义
数量积的
几何意义
数量积的性质
数量积的运算律
数量积
等于
的长度
与
在
的方向上的投影
的乘积
为非零向量,
为单位向量
①
②
③
已知两个非零向量
,在平面中任取一点
,
,则角
叫做向量
的夹角,记作:
①
②
③
新课讲授
空间向量
夹角
数量积定义
数量积的
几何意义
数量积的性质
数量积的运算律
数量积
等于
的长度
与
在
的方向上的投影
的乘积
为非零向量,
为单位向量
①
②
③
已知两个非零向量
,在空间中任取一点
,
,则角
叫做向量
的夹角,记作:
①
②
③
例1
C
例1
例2
例1
A
B
C
D
E
F
G
例2
互动探究2
求异面直线AB和CD所成的角.
例3
小结:
①
②
也有下列两个重要性质
作业:
课本P105
习题3.1
2
学案P48
例3
