2020-2021学年人教版数学七年级下册6.3.2实数的运算课件(20张)
文档属性
| 名称 | 2020-2021学年人教版数学七年级下册6.3.2实数的运算课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 587.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 11:46:57 | ||
图片预览








文档简介
(共20张PPT)
实数的概念及运算
1、实数的分类?
2、数轴的三要素是什么?
原点、正方向和单位长度。
数轴上的点与实数一一对应。
3、理解一个数的相反数,倒数及绝对值.
⑴只有符号不同的两个数是
互为相反数,
即位于原点的两侧,与原点距离相等.
⑵积为1的两个数互为倒数.
⑶一个数所对应的点与原点的距离是这个
数的绝对值.
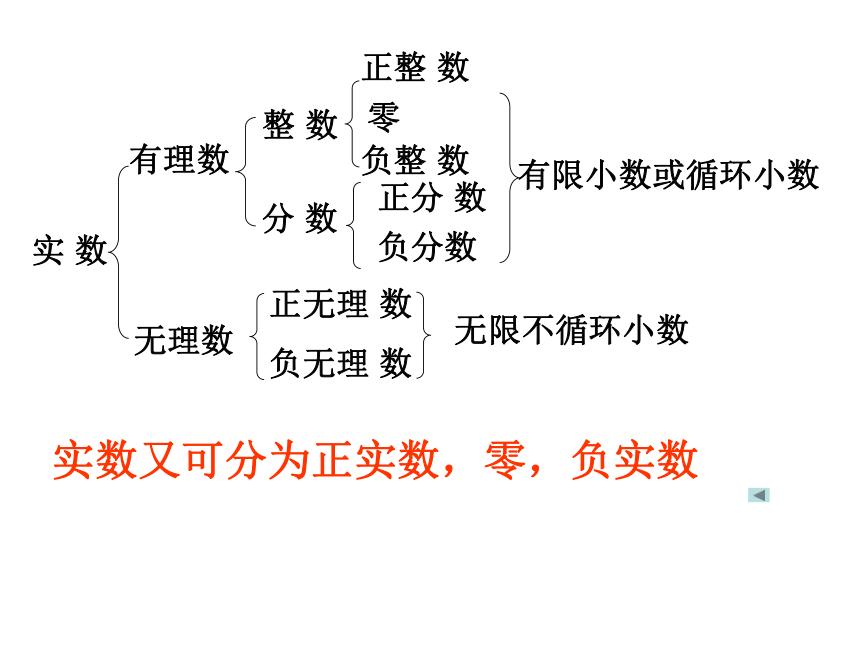
实
数
整
数
分
数
正整
数
负整
数
负分数
正分
数
正无理
数
负无理
数
有限小数或循环小数
无限不循环小数
有理数
无理数
实数又可分为正实数,零,负实数
零
4、请说一说如何求一个数的相反数,倒数及绝对值.
相反数:正数的相反数是负数,负数的相反数是正数,零的相反数是零.
倒数:1除以一个数得到这个数的倒数.
绝对值:正数的绝对值是它本身,负数的绝对值是它的相反数,零的绝对值是零.
5、实数的大小比较
数轴上右边的点表示的数总是大于左边的点表示的数,既正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
6、了解平方根,算术平方根,立方根的概念,会用根号表示数的平方根,算术平方根,立方根.
每个实数都可以用数轴上的点来表示,数轴上的每个点都表示一个实数,但不一定是有理数,
①平方根:若一个数
的平方等于
即
,则这个数
叫
的平方根(也叫二次方根),记作
读作“正负根号
”
(零的平方根是零,一个正数有两个平方根,负数没有平方根)
(零的算术平方根是零,一个正数有一个算术平方根,负数没有算术平方根)
②算术平方根:一个正数
的平方等于
即
,则这个正数
叫
的算术平方根,
,读作“根号
”
记作
③立方根:若一个数
的立方等于
,即
,则这个数
叫
的立方根
(也叫三次方根)
,读作
的立方根或三次方根.
记作
(零的立方根是零,正数的立方根是正数,负数的立方根是负数)
7、有效数字的含义
从左边第一个不是零的数字开始,到最后一个数为止都是有效数字.
8、科学记数法的表示:
是整数
典型例题
例1:如果零上2℃,记作+2℃,那么零下3℃,就记作
______.
例2:在实数-1,
sin45°,
中,无理数的是_________
正有理数是______________
例3:
的倒数为_______
的立方根为___
的平方根为______
的算术平方根为____
⑵
⑴
⑶
⑷
-3℃
sin45°,
,
2
2
例4:实数a,b在数轴上的位置如图所示
a
b
0
那么化简
的结果是(
)
B、
C、
D、
A、
例5:比较两个实数的大小:
_________
___
3.14
﹤
﹥
D
a
b
0
例6:
的小数部分为________
例7:已知a,b是互为相反数,c,d是互为倒数,
e是非零实数,
求
的值.
(0)
例8:2003年广州市完成国内生产总值(GDP)
达3466.53亿元,用四舍五入法取的近似值,
保留三个有效数字,并用科学记数法表示
的结果____________元
3.47×1011
9、实数的各运算法则:
加法法则,同号两数相加,
取相同的加数的符号,并把绝对值相加,
异号两数相加,绝对值相等时和为零,
绝对值不等时,取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值,
一个数同零相加,仍得这个数,
互为相反数的两数相加得零.
②减法法则:减去一个数,等于加上这个数的相反数.
③乘法法则:两数相乘,同号得正,
异号得负,并把绝对值相乘。
④有理数的除法法则:除以一个非零数等于
乘以这个数的倒数(小数一般以分数的结果出现)。
⑤乘方运算:求几个相同因数的积的运算。即
中,
叫做底数,n叫做指数,
叫做幂,读做
的n次幂或
的n次方
(底数为负数或分数时要用小括号括起来)
⑥二次根式的运算法则
11、实数的运算律:
10、实数的运算顺序
先算乘方,再算乘除,最后算加减,
若有括号,要先算括号里面的。
(1)加法的交换律:a+b=b+a
(2)加法的结合律:(a+b)+c=a+(b+c)
(3)乘法的交换律:ab=ba
(4)加法的结合律:(ab)c=a(bc)
(5)乘法对加法的分配律:a(b+c)=ab+ac
例9:
计算:
例10:规定一种新的运算:a□b=ab-a-b+1
如3□4=3×4-3-4+1
请比较大小:
(-3)□4
___
4□(-3)
(填﹤,﹥,=)
例11:a=
求a2+4a的值.
3
=
1
例12:
的整数部分为a,小数部分为b,
则a-b的值为
________
例13:下列二次根式中
中与
是同类二次根式的个数为_____
例14:下列是最简二次根式的是(
)
B、
C、
D、
A、
C
2个
例15:观察下列各式:
…请你将规律用含自然数n(n
≥
1)
的式子表示出来________
1.练习卷.
独立
作业
温馨提醒
祝你成功!
再见
实数的概念及运算
1、实数的分类?
2、数轴的三要素是什么?
原点、正方向和单位长度。
数轴上的点与实数一一对应。
3、理解一个数的相反数,倒数及绝对值.
⑴只有符号不同的两个数是
互为相反数,
即位于原点的两侧,与原点距离相等.
⑵积为1的两个数互为倒数.
⑶一个数所对应的点与原点的距离是这个
数的绝对值.
实
数
整
数
分
数
正整
数
负整
数
负分数
正分
数
正无理
数
负无理
数
有限小数或循环小数
无限不循环小数
有理数
无理数
实数又可分为正实数,零,负实数
零
4、请说一说如何求一个数的相反数,倒数及绝对值.
相反数:正数的相反数是负数,负数的相反数是正数,零的相反数是零.
倒数:1除以一个数得到这个数的倒数.
绝对值:正数的绝对值是它本身,负数的绝对值是它的相反数,零的绝对值是零.
5、实数的大小比较
数轴上右边的点表示的数总是大于左边的点表示的数,既正数大于一切负数和零,零大于一切负数,两个负数比较绝对值大的反而小。
6、了解平方根,算术平方根,立方根的概念,会用根号表示数的平方根,算术平方根,立方根.
每个实数都可以用数轴上的点来表示,数轴上的每个点都表示一个实数,但不一定是有理数,
①平方根:若一个数
的平方等于
即
,则这个数
叫
的平方根(也叫二次方根),记作
读作“正负根号
”
(零的平方根是零,一个正数有两个平方根,负数没有平方根)
(零的算术平方根是零,一个正数有一个算术平方根,负数没有算术平方根)
②算术平方根:一个正数
的平方等于
即
,则这个正数
叫
的算术平方根,
,读作“根号
”
记作
③立方根:若一个数
的立方等于
,即
,则这个数
叫
的立方根
(也叫三次方根)
,读作
的立方根或三次方根.
记作
(零的立方根是零,正数的立方根是正数,负数的立方根是负数)
7、有效数字的含义
从左边第一个不是零的数字开始,到最后一个数为止都是有效数字.
8、科学记数法的表示:
是整数
典型例题
例1:如果零上2℃,记作+2℃,那么零下3℃,就记作
______.
例2:在实数-1,
sin45°,
中,无理数的是_________
正有理数是______________
例3:
的倒数为_______
的立方根为___
的平方根为______
的算术平方根为____
⑵
⑴
⑶
⑷
-3℃
sin45°,
,
2
2
例4:实数a,b在数轴上的位置如图所示
a
b
0
那么化简
的结果是(
)
B、
C、
D、
A、
例5:比较两个实数的大小:
_________
___
3.14
﹤
﹥
D
a
b
0
例6:
的小数部分为________
例7:已知a,b是互为相反数,c,d是互为倒数,
e是非零实数,
求
的值.
(0)
例8:2003年广州市完成国内生产总值(GDP)
达3466.53亿元,用四舍五入法取的近似值,
保留三个有效数字,并用科学记数法表示
的结果____________元
3.47×1011
9、实数的各运算法则:
加法法则,同号两数相加,
取相同的加数的符号,并把绝对值相加,
异号两数相加,绝对值相等时和为零,
绝对值不等时,取绝对值较大的数的符号,
并用较大的绝对值减去较小的绝对值,
一个数同零相加,仍得这个数,
互为相反数的两数相加得零.
②减法法则:减去一个数,等于加上这个数的相反数.
③乘法法则:两数相乘,同号得正,
异号得负,并把绝对值相乘。
④有理数的除法法则:除以一个非零数等于
乘以这个数的倒数(小数一般以分数的结果出现)。
⑤乘方运算:求几个相同因数的积的运算。即
中,
叫做底数,n叫做指数,
叫做幂,读做
的n次幂或
的n次方
(底数为负数或分数时要用小括号括起来)
⑥二次根式的运算法则
11、实数的运算律:
10、实数的运算顺序
先算乘方,再算乘除,最后算加减,
若有括号,要先算括号里面的。
(1)加法的交换律:a+b=b+a
(2)加法的结合律:(a+b)+c=a+(b+c)
(3)乘法的交换律:ab=ba
(4)加法的结合律:(ab)c=a(bc)
(5)乘法对加法的分配律:a(b+c)=ab+ac
例9:
计算:
例10:规定一种新的运算:a□b=ab-a-b+1
如3□4=3×4-3-4+1
请比较大小:
(-3)□4
___
4□(-3)
(填﹤,﹥,=)
例11:a=
求a2+4a的值.
3
=
1
例12:
的整数部分为a,小数部分为b,
则a-b的值为
________
例13:下列二次根式中
中与
是同类二次根式的个数为_____
例14:下列是最简二次根式的是(
)
B、
C、
D、
A、
C
2个
例15:观察下列各式:
…请你将规律用含自然数n(n
≥
1)
的式子表示出来________
1.练习卷.
独立
作业
温馨提醒
祝你成功!
再见
