6.1圆周运动—2020-2021学年【新教材】人教版(2019)高中物理必修二课件26张PPT
文档属性
| 名称 | 6.1圆周运动—2020-2021学年【新教材】人教版(2019)高中物理必修二课件26张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-03-25 17:18:58 | ||
图片预览








文档简介
6.1 圆周运动
一、圆周运动
1、定义:质点运动轨迹是圆或圆的一部分的运动。
2、常见:最简单的是匀速圆周运动。
3、特征:质点的轨迹是圆周、具有周期性
将自行车后轮架起,转动脚踏板,注意观察:
(1)大、小两个齿轮边缘上的点,哪个运动得更快些?
(2)同一个齿轮上到转轴的距离不同的点,
哪个运动得更快些?
(3)你能说出判断运动快慢的依据吗?
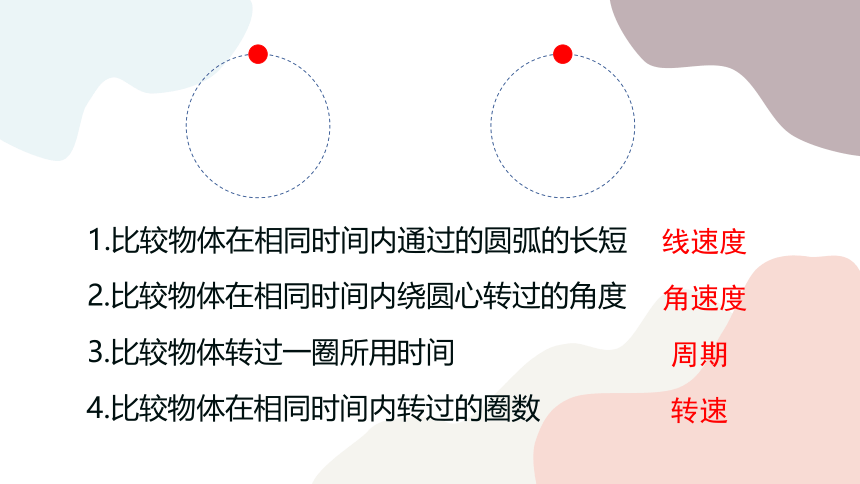
两物体均做圆周运动,
怎样比较它们运动的快慢?
1.比较物体在相同时间内通过的圆弧的长短
2.比较物体在相同时间内绕圆心转过的角度
3.比较物体转过一圈所用时间
4.比较物体在相同时间内转过的圈数
线速度
角速度
周期
转速
在图 6.1-1 中,物体沿圆弧由 M 向 N 运动,在某时刻 t 经过 A 点。为了描述物体经过 A 点附近时运动的快慢,可以取一段很短的时间 Δt,物体在这段时间内由 A 运动到B,通过的弧长为 Δs。弧长 Δs 与时间 Δt 之比反映了物体在 A 点附近运动的快慢,如果 Δt 非常非常小,Δs/ Δt
就可以表示物体在 A 点时运动的快慢,
通常把它称为线速度的大小,用符号 v 表示,
1、物理意义:描述质点沿圆周运动的快慢。
2、定义:质点做圆周运动通过的弧长 ΔS和所用时间 Δt 的比值叫做线速度。
3、大小:
4、单位:m/s
5、方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向。
ΔS是弧长并非位移
当Δt 很小很小时(趋近零),弧长Δs就等于物体的位移,式中的v ,就是直线运动中学过的瞬时速度。
?s
二、线速度
矢量
航天员在太空做了一个有趣的实验:用长度大约为32cm的细绳拴着一颗小钢球,细绳恰好处于伸直状态,航天员用手指沿垂直细绳方向轻推小球,小球在拉力作用下沿某一平面做匀速圆周运动,2s 转动一圈,由此可估测出小球线速度大小约为( )
A. 0.1m/s B.0.5m/s C.1m/s D.2m/s
√
v
v
v
o
定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
率
匀速圆周运动中的“匀速”指速度不变吗?
注意:匀速圆周运动是一种变速曲线运动
加速度方向在变化
物体在做匀速圆周运动的过程中,关于其线速度的说法正确的是( )
A. 大小保持不变,方向时刻改变
B. 大小时刻改变,方向保持不变
C. 大小、方向均保持不变
D. 大小、方向均时刻改变
√
自行车前进时,由于链条不可伸长,也不会脱离齿轮打滑(图 6.1-2),因而大、小齿轮边缘的点在相等时间内通过的弧长是相等的,即线速度大小相等。
但同时也可注意到,由于两个齿轮
的半径不同,相等时间内它们转过
的角度不同。我们引入角速度这个
物理量来描述做圆周运动的物体绕
圆心转动的快慢。
三、角速度
5、物理意义:描述物体绕圆心转动的快慢。
?
2、大小:
4、单位:弧度/秒 (rad/s)
?
Δ
θ
A
B
国际单位用弧度制
3、矢量:角速度有方向,但高中阶段不做了解。
圆心角θ的大小可以用弧长和半径的比值来描述,这个比值是没有单位的,为了描述问题的方便,我们“给”这个比值一个单位,这就是弧度(rad).
R
l
=
=
半径
弧长
q
角度制和弧度制
2、弧度制:
1、角度制:将圆周等分成360等份,
每一等份对应的圆心角定义为1度。
1、周期:做匀速圆周运动的物体,运动(一周)所用的时间,用T表示,单位是秒(s)
2、转速:物体转动的(圈数)与所用(时间)之比,用n表示,单位为转每秒(r/s)或转每分(r/min) 。
3、频率:物体单位时间内完成的圆周运动的(次数)又称为频率,用f表示。当转速的单位取r/s时,转速的数值与频率(相同)。
四、 周期、转速、频率
转速
周期
频率
定义
符号
单位
物理意义
关系
物体在单位时间所转过的圈数
n
r/s或r/min
描述物体做圆周运动的快慢
物体运动一周所用的时间
物体在单位时间所转过的圈数
T
f
s
Hz或s-1
n = f =
T
1
匀速圆周运动是周期、频率、转速都不变的运动!
五、v、ω、T(f、n)的关系
线速度与角速度的关系?
设物体做半径为 r 的匀速圆周运动,在 Δt 内通过的弧长为 Δs ,半径转过的角度为 Δθ
由数学知识得 Δs = rΔθ
v = = = ωr
Δt
Δs
Δt
rΔ
θ
v = ωr
?s
Δ
θ
r
线速度、角速度与周期的关系?
设物体做半径为 r 的匀速圆周运动:
线速度与周期的关系:
角速度与周期的关系:
v = ωr
ω=
T
2π
= 2πf = 2πn
v =
T
2πr
= 2πrf = 2πrn
当 v 一定时,ω 与 r 成反比
当 ω 一定时,v 与 r 成正比
当 r 一定时,v 与 ω 成正比
关于v=ωr的讨论:
根据上面的公式,得出速度V与角速度ω成正比,你同意这种说法吗?请说出你的理由.
小结:
六、两个重要的结论
1.同一传动
皮带传动
齿轮传动
(相等时间里转过的弧长相等)
同一传动各轮边缘上线速度相同
?
?
?
2.同轴转动
(相等时间里转过的角度相等)
同轴转动各点的角速度相同
?
?
?
(多选)如图4所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,则A、B、C三轮边缘上a、b、c三点的
A.角速度之比为1∶2∶2
B.角速度之比为1∶1∶2
C.线速度大小之比为1∶2∶2
D.线速度大小之比为1∶1∶2
√
图4
√
常见的传动装置及其特点
?
同轴传动
皮带传动
齿轮传动
装置
A、B两点在同轴的一个圆盘上
两个轮子用皮带连接,A、B两点分别是两个轮子边缘上的点
两个齿轮啮合,A、B两点分别是两个齿轮边缘上的点
特点
角速度、周期相同
线速度大小相同
线速度大小相同
规律
线速度与半径成正比:
角速度与
半径成反比:
周期与
半径成正比:
角速度与
半径成反比:
周期与
半径成正比:
4.两物体做匀速圆周运动,运动半径之比为4︰3,角速度之比为3︰4,则这两物体的线速度之比为( )
A.16︰9 B.9︰16 C.1︰1 D.4︰3
√
如图所示,主动轮M通过皮带带动从动轮N做匀速转动,a是M轮上距轴O1的距离等于M轮半径一半的点,b、c分别是N轮和M轮轮缘上的点,已知在皮带不打滑的情况下,N轮的转速是M轮的3倍,则( )
A.a、b两点的角速度之比为3:1
B.a、b两点的线速度之比为1:2
C.b、c两点的周期之比为1:3
D.a、c两点的线速度之比为1:3
√
√
A、B两质点分别做匀速圆周运动,若它们在相等的时间内通过的弧长之比为1:2,而转过的圆心角之比为2:1,则它们的线速度之比________,角速度之比_________,它们做圆周运动的半径之比为_______,周期之比________,转速之比_________。
1:2
2:1
1:4
1:2
2:1
一、圆周运动
1、定义:质点运动轨迹是圆或圆的一部分的运动。
2、常见:最简单的是匀速圆周运动。
3、特征:质点的轨迹是圆周、具有周期性
将自行车后轮架起,转动脚踏板,注意观察:
(1)大、小两个齿轮边缘上的点,哪个运动得更快些?
(2)同一个齿轮上到转轴的距离不同的点,
哪个运动得更快些?
(3)你能说出判断运动快慢的依据吗?
两物体均做圆周运动,
怎样比较它们运动的快慢?
1.比较物体在相同时间内通过的圆弧的长短
2.比较物体在相同时间内绕圆心转过的角度
3.比较物体转过一圈所用时间
4.比较物体在相同时间内转过的圈数
线速度
角速度
周期
转速
在图 6.1-1 中,物体沿圆弧由 M 向 N 运动,在某时刻 t 经过 A 点。为了描述物体经过 A 点附近时运动的快慢,可以取一段很短的时间 Δt,物体在这段时间内由 A 运动到B,通过的弧长为 Δs。弧长 Δs 与时间 Δt 之比反映了物体在 A 点附近运动的快慢,如果 Δt 非常非常小,Δs/ Δt
就可以表示物体在 A 点时运动的快慢,
通常把它称为线速度的大小,用符号 v 表示,
1、物理意义:描述质点沿圆周运动的快慢。
2、定义:质点做圆周运动通过的弧长 ΔS和所用时间 Δt 的比值叫做线速度。
3、大小:
4、单位:m/s
5、方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向。
ΔS是弧长并非位移
当Δt 很小很小时(趋近零),弧长Δs就等于物体的位移,式中的v ,就是直线运动中学过的瞬时速度。
?s
二、线速度
矢量
航天员在太空做了一个有趣的实验:用长度大约为32cm的细绳拴着一颗小钢球,细绳恰好处于伸直状态,航天员用手指沿垂直细绳方向轻推小球,小球在拉力作用下沿某一平面做匀速圆周运动,2s 转动一圈,由此可估测出小球线速度大小约为( )
A. 0.1m/s B.0.5m/s C.1m/s D.2m/s
√
v
v
v
o
定义:物体沿着圆周运动,并且线速度的大小处处相等,这种运动叫做匀速圆周运动。
率
匀速圆周运动中的“匀速”指速度不变吗?
注意:匀速圆周运动是一种变速曲线运动
加速度方向在变化
物体在做匀速圆周运动的过程中,关于其线速度的说法正确的是( )
A. 大小保持不变,方向时刻改变
B. 大小时刻改变,方向保持不变
C. 大小、方向均保持不变
D. 大小、方向均时刻改变
√
自行车前进时,由于链条不可伸长,也不会脱离齿轮打滑(图 6.1-2),因而大、小齿轮边缘的点在相等时间内通过的弧长是相等的,即线速度大小相等。
但同时也可注意到,由于两个齿轮
的半径不同,相等时间内它们转过
的角度不同。我们引入角速度这个
物理量来描述做圆周运动的物体绕
圆心转动的快慢。
三、角速度
5、物理意义:描述物体绕圆心转动的快慢。
?
2、大小:
4、单位:弧度/秒 (rad/s)
?
Δ
θ
A
B
国际单位用弧度制
3、矢量:角速度有方向,但高中阶段不做了解。
圆心角θ的大小可以用弧长和半径的比值来描述,这个比值是没有单位的,为了描述问题的方便,我们“给”这个比值一个单位,这就是弧度(rad).
R
l
=
=
半径
弧长
q
角度制和弧度制
2、弧度制:
1、角度制:将圆周等分成360等份,
每一等份对应的圆心角定义为1度。
1、周期:做匀速圆周运动的物体,运动(一周)所用的时间,用T表示,单位是秒(s)
2、转速:物体转动的(圈数)与所用(时间)之比,用n表示,单位为转每秒(r/s)或转每分(r/min) 。
3、频率:物体单位时间内完成的圆周运动的(次数)又称为频率,用f表示。当转速的单位取r/s时,转速的数值与频率(相同)。
四、 周期、转速、频率
转速
周期
频率
定义
符号
单位
物理意义
关系
物体在单位时间所转过的圈数
n
r/s或r/min
描述物体做圆周运动的快慢
物体运动一周所用的时间
物体在单位时间所转过的圈数
T
f
s
Hz或s-1
n = f =
T
1
匀速圆周运动是周期、频率、转速都不变的运动!
五、v、ω、T(f、n)的关系
线速度与角速度的关系?
设物体做半径为 r 的匀速圆周运动,在 Δt 内通过的弧长为 Δs ,半径转过的角度为 Δθ
由数学知识得 Δs = rΔθ
v = = = ωr
Δt
Δs
Δt
rΔ
θ
v = ωr
?s
Δ
θ
r
线速度、角速度与周期的关系?
设物体做半径为 r 的匀速圆周运动:
线速度与周期的关系:
角速度与周期的关系:
v = ωr
ω=
T
2π
= 2πf = 2πn
v =
T
2πr
= 2πrf = 2πrn
当 v 一定时,ω 与 r 成反比
当 ω 一定时,v 与 r 成正比
当 r 一定时,v 与 ω 成正比
关于v=ωr的讨论:
根据上面的公式,得出速度V与角速度ω成正比,你同意这种说法吗?请说出你的理由.
小结:
六、两个重要的结论
1.同一传动
皮带传动
齿轮传动
(相等时间里转过的弧长相等)
同一传动各轮边缘上线速度相同
?
?
?
2.同轴转动
(相等时间里转过的角度相等)
同轴转动各点的角速度相同
?
?
?
(多选)如图4所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三个轮的半径关系是rA=rC=2rB.若皮带不打滑,则A、B、C三轮边缘上a、b、c三点的
A.角速度之比为1∶2∶2
B.角速度之比为1∶1∶2
C.线速度大小之比为1∶2∶2
D.线速度大小之比为1∶1∶2
√
图4
√
常见的传动装置及其特点
?
同轴传动
皮带传动
齿轮传动
装置
A、B两点在同轴的一个圆盘上
两个轮子用皮带连接,A、B两点分别是两个轮子边缘上的点
两个齿轮啮合,A、B两点分别是两个齿轮边缘上的点
特点
角速度、周期相同
线速度大小相同
线速度大小相同
规律
线速度与半径成正比:
角速度与
半径成反比:
周期与
半径成正比:
角速度与
半径成反比:
周期与
半径成正比:
4.两物体做匀速圆周运动,运动半径之比为4︰3,角速度之比为3︰4,则这两物体的线速度之比为( )
A.16︰9 B.9︰16 C.1︰1 D.4︰3
√
如图所示,主动轮M通过皮带带动从动轮N做匀速转动,a是M轮上距轴O1的距离等于M轮半径一半的点,b、c分别是N轮和M轮轮缘上的点,已知在皮带不打滑的情况下,N轮的转速是M轮的3倍,则( )
A.a、b两点的角速度之比为3:1
B.a、b两点的线速度之比为1:2
C.b、c两点的周期之比为1:3
D.a、c两点的线速度之比为1:3
√
√
A、B两质点分别做匀速圆周运动,若它们在相等的时间内通过的弧长之比为1:2,而转过的圆心角之比为2:1,则它们的线速度之比________,角速度之比_________,它们做圆周运动的半径之比为_______,周期之比________,转速之比_________。
1:2
2:1
1:4
1:2
2:1
