小考复习教案 速算巧算
图片预览



文档简介
第三讲:速算、巧算和新定义运算
专题简析:
这一讲,我们主要讲解各种计算技巧和新定义运算,其中我们要讲到的计算技巧包括:观察法、灵活利用运算律、裂项法、公式法等方法。新定义运算我们将结合几个常见的新定义种类和大家探讨这类问题的解题思路。
观察法:需要我们在审题时注意观察算式的构成,灵活运用我们所学过的运算律来解题。
例题1:计算333387×79+790×66661
原式=333387.5×79+790×66661.25
=(33338.75+66661.25)×790
=100000×790
=79000000
练习1:1. 3.5×1+125%+1÷ 2. 975×0.25+9×76-9.75
例题2:计算:36×1.09+1.2×67.3
原式=1.2×30×1.09+1.2×67.3
=1.2×(32.7+67.3)
=1.2×100
=120
练习2::计算:
1. 45×2.08+1.5×37.6 2. 52×11.1+2.6×778
例题3:计算20112011×2012-20122012×2011
分析与解答:这道题如果直接计算,显得比较麻烦。根据题中的数的特点,如果把20112011变形为2011×10001,把20122012变形为2012×10001,那么计算起来就非常方便。
20112011×2012-20122012×2011
=2011×10001×2012-2012×10001×2011
=0
练习3:计算题:192192×368-368368×192
例题4:计算81.5×15.8+81.5×51.8+67.6×18.5
原式=81.5×(15.8+51.8)+67.6×18.5
=81.5×67.6+67.6×18.5
=(81.5+18.5)×67.6
=100×67.6
=6760
练习4:
53.5×35.3+53.5×43.2+78.5×46.5
运算律法:这一种方法我们在课本中已经反复练习,我们这里主要讲解如何灵活运用运算律。不但要会用,更加要会巧用。
例题1:计算:1234+2341+3412+4123
简析 注意到题中共有4个四位数,每个四位数中都包含有1、2、3、4这几个数字,而且它们都分别在千位、百位、十位、个位上出现了一次,根据位值计数的原则,可作如下解答:
原式=1×1111+2×1111+3×1111+4×1111
=(1+2+3+4)×1111
=10×1111
=11110
练习1
23456+34562+45623+56234+62345
例题2:计算:2×23.4+11.1×57.6+6.54×28
原式=2.8×23.4+2.8×65.4+11.1×8×7.2
=2.8×(23.4+65.4)+88.8× 7.2
=2.8×88.8+88.8×7.2
=88.8×(2.8+7.2)
=88.8×10
=888
练习2
99999×77778+33333×66666
77×13+255×999+510
例题3:计算
原式=
=
=1
练习3:
1.
例题4:有一串数1,4,9,16,25,36…….它们是按一定的规律排列的,那么其中第2000个数与2001个数相差多少?
20012-20002=2001×2000-20002+2001
=2000×(2001-2000)+2001
=2000+2001
=4001
练习4
计算:
1. 19912-19902 2. 99992+19999 3. 999×274+6274
例题5:计算:(9+7)÷(+)
原式=(+)÷(+)
=【65×(+)】÷【5×(+)】
=65÷5
=13
练习5
(+1+)÷(++)
(3+1)÷(1+)
例题6:计算:(1)×37 (2) 27×
(1) 原式=(1-)×37 (2) 原式=(26+1)×
=1×37-×37 =26×+
=37- =15+
=36 =15
练习6:
用简便方法计算下面各题:
1. ×8 2. ×126 3. 35×
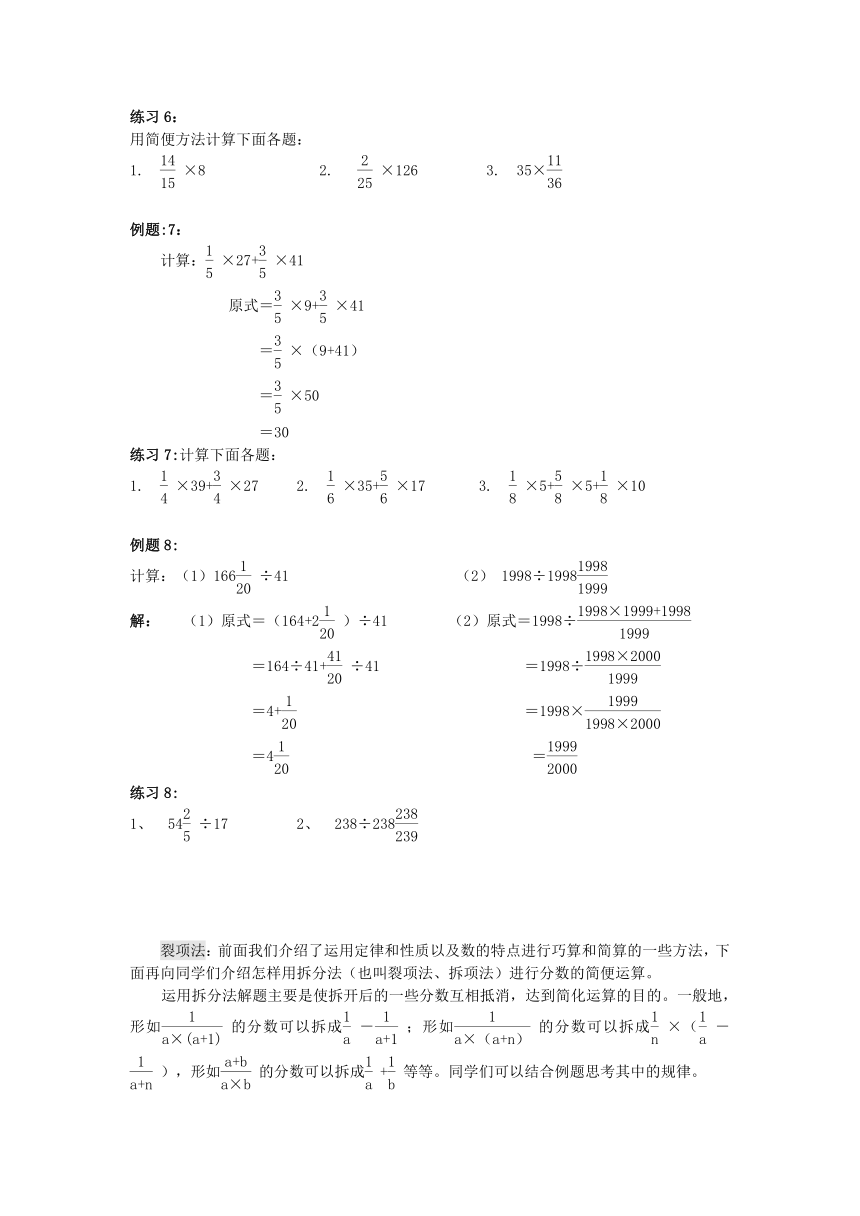
例题:7:
计算:×27+×41
原式=×9+×41
=×(9+41)
=×50
=30
练习7:计算下面各题:
1. ×39+×27 2. ×35+×17 3. ×5+×5+×10
例题8:
计算:(1)166÷41 (2) 1998÷1998
解: (1)原式=(164+2)÷41 (2)原式=1998÷
=164÷41+÷41 =1998÷
=4+ =1998×
=4 =
练习8:
1、 54÷17 2、 238÷238
裂项法:前面我们介绍了运用定律和性质以及数的特点进行巧算和简算的一些方法,下面再向同学们介绍怎样用拆分法(也叫裂项法、拆项法)进行分数的简便运算。
运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。一般地,形如的分数可以拆成-;形如的分数可以拆成×(-),形如的分数可以拆成+等等。同学们可以结合例题思考其中的规律。
例题1:
计算:+++…..+
原式=(1-)+(-)+(-)+…..+ (-)
=1-+-+-+…..+ -
=1-
=
练习1:
1. +++…..+
2. +++ +
例题2:
计算:+++…..+
原式=(+++…..+ )×
=【(-)+(-)+(-)…..+ (-)】×
=【-】×
=
练习2:
1. +++…..+
2. +++…..+
例题3:
计算:1-+-+-
原式=1-(+)+(+)-(+)+(+)-(+)
=1--++--++--
=1-
=
练习3:
计算下面各题:
1+-+- 2.1-+-+
例题4:计算:+++++
原式=(++++++)-
=1-
=
练习4
1. +++………+
例题5:计算:(1+++)×(+++)-(1++++)×(++)
设1+++=a ++=b
原式=a×(b+)-(a+)×b
=ab+a-ab-b
=(a-b)
=
练习5
(+++)×(+++)-(++++)×(++)
公式法:若干个数排成一列称为数列。数列中的每一个数称为一项。其中第一项称为首项,最后一项称为末项,数列中项的个数称为项数。从第二项开始,后项与其相邻的前项之差都相等的数列称为等差数列,后项与前项的差称为公差。
在这一章要用到两个非常重要的公式:“通项公式”和“项数公式”。
通项公式:
第n项=首项+(项数-1)×公差
项数公式:
项数=(末项-首项)÷公差+1
例1:有一个数列:4,10,16,22,…,52,这个数列共有多少项?
分析与解答:容易看出这是一个等差数列,公差为6,首项是4,末项是52,要求项数,可直接带入项数公式进行计算。
项数=(52-4)÷6+1=9,即这个数列共有9项。
练习1:等差数列中,首项=1,末项=39,公差=2,这个等差数列共有多少项?
例2:有一等差数列:3,7,11,15,……,这个等差数列的第100项是多少?
分析与解答:这个等差数列的首项是3,公差是4,项数是100。要求第100项,可根据“末项=首项+公差×(项数-1)”进行计算。
第100项=3+4×(100-1)=399
练习2:一等差数列,首项=3,公差=2,项数=10,它的末项是多少?
例3:有这样一个数列:1,2,3,4,…,99,100。请求出这个数列所有项的和。
分析与解答:如果我们把1,2,3,4,…,99,100与列100,99,…,3,2,1相加,则得到(1+100)+(2+99)+(3+98)+…+(99+2)+(100+1),其中每个小括号内的两个数的和都是101,一共有100个101相加,所得的和就是所求数列的和的2倍,再除以2,就是所求数列的和。
1+2+3+…+99+100=(1+100)×100÷2=5050
练习3:求100+99+98+…+61+60的值
题型补充:求1 ~ 99 这99个连续自然数的所有数字之和。
分析与解答:首先应该弄清楚这题是求99个连续自然数的数字之和,而不是求这99个数之和。为了能方便地解决问题,我们不妨把0算进来(它不影响我们计算数字之和)计算0~99这100个数的数字之和。这100个数头尾两配对后每两个数的数字之和都相等,是9+9=18,一共有100÷2=50对,所以,1~99这99个连续自然数的所有数字之和是18×50=900。
练习四
1.求1~199这199个连续自然数的所有数字之和。
新定义简析:
定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些特殊算式的一种运算。
解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、等,这是与四则运算中的“、、、·”不同的。
新定义的算式中有括号的,要先算括号里面的。但它在没有转化前,是不适合于各种运算定律的。
例题1:
假设a*b=(a+b)+(a-b),求13*5和13*(5*4)。
13*5=(13+5)+(13-5)=18+8=26
5*4=(5+4)+(5-4)=10
13*(5*4)=13*10=(13+10)+(13-10)=26
练习1
1..将新运算“*”定义为:a*b=(a+b)×(a-b).求27*9。
例题2:
设p、q是两个数,规定:p△q=4×q-(p+q)÷2。求3△(4△6).
3△(4△6).
=3△【4×6-(4+6)÷2】
=3△19
=4×19-(3+19)÷2
=76-11
=65
练习2:
设p、q是两个数,规定p△q=4×q-(p+q)÷2,求5△(6△4)。
例题3:
如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,4*2=4+44。那么7*4=?,210*2=?
7*4=7+77+777+7777=8638
210*2=210+210210=210420
练习3:
如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,…..那么,4*4=?,18*3=?
例题4:
规定②=1×2×3,③=2×3×4 ,④=3×4×5,⑤=4×5×6,……如果 EQ \F(1,⑥) - EQ \F(1,⑦) = EQ \F(1,⑦) ×A,那么A是几?
A =( EQ \F(1,⑥) - EQ \F(1,⑦) )÷ EQ \F(1,⑦)
=( EQ \F(1,⑥) - EQ \F(1,⑦) )×⑦
= EQ \F(⑦,⑥) -1
=-1
=
练习4
规定:②=1×2×3,③=2×3×4,④=3×4×5,⑤=4×5×6,……..如果 EQ \F(1,⑧) - EQ \F(1,⑨) = EQ \F(1,⑨) ×A,那么A=?。
专题简析:
这一讲,我们主要讲解各种计算技巧和新定义运算,其中我们要讲到的计算技巧包括:观察法、灵活利用运算律、裂项法、公式法等方法。新定义运算我们将结合几个常见的新定义种类和大家探讨这类问题的解题思路。
观察法:需要我们在审题时注意观察算式的构成,灵活运用我们所学过的运算律来解题。
例题1:计算333387×79+790×66661
原式=333387.5×79+790×66661.25
=(33338.75+66661.25)×790
=100000×790
=79000000
练习1:1. 3.5×1+125%+1÷ 2. 975×0.25+9×76-9.75
例题2:计算:36×1.09+1.2×67.3
原式=1.2×30×1.09+1.2×67.3
=1.2×(32.7+67.3)
=1.2×100
=120
练习2::计算:
1. 45×2.08+1.5×37.6 2. 52×11.1+2.6×778
例题3:计算20112011×2012-20122012×2011
分析与解答:这道题如果直接计算,显得比较麻烦。根据题中的数的特点,如果把20112011变形为2011×10001,把20122012变形为2012×10001,那么计算起来就非常方便。
20112011×2012-20122012×2011
=2011×10001×2012-2012×10001×2011
=0
练习3:计算题:192192×368-368368×192
例题4:计算81.5×15.8+81.5×51.8+67.6×18.5
原式=81.5×(15.8+51.8)+67.6×18.5
=81.5×67.6+67.6×18.5
=(81.5+18.5)×67.6
=100×67.6
=6760
练习4:
53.5×35.3+53.5×43.2+78.5×46.5
运算律法:这一种方法我们在课本中已经反复练习,我们这里主要讲解如何灵活运用运算律。不但要会用,更加要会巧用。
例题1:计算:1234+2341+3412+4123
简析 注意到题中共有4个四位数,每个四位数中都包含有1、2、3、4这几个数字,而且它们都分别在千位、百位、十位、个位上出现了一次,根据位值计数的原则,可作如下解答:
原式=1×1111+2×1111+3×1111+4×1111
=(1+2+3+4)×1111
=10×1111
=11110
练习1
23456+34562+45623+56234+62345
例题2:计算:2×23.4+11.1×57.6+6.54×28
原式=2.8×23.4+2.8×65.4+11.1×8×7.2
=2.8×(23.4+65.4)+88.8× 7.2
=2.8×88.8+88.8×7.2
=88.8×(2.8+7.2)
=88.8×10
=888
练习2
99999×77778+33333×66666
77×13+255×999+510
例题3:计算
原式=
=
=1
练习3:
1.
例题4:有一串数1,4,9,16,25,36…….它们是按一定的规律排列的,那么其中第2000个数与2001个数相差多少?
20012-20002=2001×2000-20002+2001
=2000×(2001-2000)+2001
=2000+2001
=4001
练习4
计算:
1. 19912-19902 2. 99992+19999 3. 999×274+6274
例题5:计算:(9+7)÷(+)
原式=(+)÷(+)
=【65×(+)】÷【5×(+)】
=65÷5
=13
练习5
(+1+)÷(++)
(3+1)÷(1+)
例题6:计算:(1)×37 (2) 27×
(1) 原式=(1-)×37 (2) 原式=(26+1)×
=1×37-×37 =26×+
=37- =15+
=36 =15
练习6:
用简便方法计算下面各题:
1. ×8 2. ×126 3. 35×
例题:7:
计算:×27+×41
原式=×9+×41
=×(9+41)
=×50
=30
练习7:计算下面各题:
1. ×39+×27 2. ×35+×17 3. ×5+×5+×10
例题8:
计算:(1)166÷41 (2) 1998÷1998
解: (1)原式=(164+2)÷41 (2)原式=1998÷
=164÷41+÷41 =1998÷
=4+ =1998×
=4 =
练习8:
1、 54÷17 2、 238÷238
裂项法:前面我们介绍了运用定律和性质以及数的特点进行巧算和简算的一些方法,下面再向同学们介绍怎样用拆分法(也叫裂项法、拆项法)进行分数的简便运算。
运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。一般地,形如的分数可以拆成-;形如的分数可以拆成×(-),形如的分数可以拆成+等等。同学们可以结合例题思考其中的规律。
例题1:
计算:+++…..+
原式=(1-)+(-)+(-)+…..+ (-)
=1-+-+-+…..+ -
=1-
=
练习1:
1. +++…..+
2. +++ +
例题2:
计算:+++…..+
原式=(+++…..+ )×
=【(-)+(-)+(-)…..+ (-)】×
=【-】×
=
练习2:
1. +++…..+
2. +++…..+
例题3:
计算:1-+-+-
原式=1-(+)+(+)-(+)+(+)-(+)
=1--++--++--
=1-
=
练习3:
计算下面各题:
1+-+- 2.1-+-+
例题4:计算:+++++
原式=(++++++)-
=1-
=
练习4
1. +++………+
例题5:计算:(1+++)×(+++)-(1++++)×(++)
设1+++=a ++=b
原式=a×(b+)-(a+)×b
=ab+a-ab-b
=(a-b)
=
练习5
(+++)×(+++)-(++++)×(++)
公式法:若干个数排成一列称为数列。数列中的每一个数称为一项。其中第一项称为首项,最后一项称为末项,数列中项的个数称为项数。从第二项开始,后项与其相邻的前项之差都相等的数列称为等差数列,后项与前项的差称为公差。
在这一章要用到两个非常重要的公式:“通项公式”和“项数公式”。
通项公式:
第n项=首项+(项数-1)×公差
项数公式:
项数=(末项-首项)÷公差+1
例1:有一个数列:4,10,16,22,…,52,这个数列共有多少项?
分析与解答:容易看出这是一个等差数列,公差为6,首项是4,末项是52,要求项数,可直接带入项数公式进行计算。
项数=(52-4)÷6+1=9,即这个数列共有9项。
练习1:等差数列中,首项=1,末项=39,公差=2,这个等差数列共有多少项?
例2:有一等差数列:3,7,11,15,……,这个等差数列的第100项是多少?
分析与解答:这个等差数列的首项是3,公差是4,项数是100。要求第100项,可根据“末项=首项+公差×(项数-1)”进行计算。
第100项=3+4×(100-1)=399
练习2:一等差数列,首项=3,公差=2,项数=10,它的末项是多少?
例3:有这样一个数列:1,2,3,4,…,99,100。请求出这个数列所有项的和。
分析与解答:如果我们把1,2,3,4,…,99,100与列100,99,…,3,2,1相加,则得到(1+100)+(2+99)+(3+98)+…+(99+2)+(100+1),其中每个小括号内的两个数的和都是101,一共有100个101相加,所得的和就是所求数列的和的2倍,再除以2,就是所求数列的和。
1+2+3+…+99+100=(1+100)×100÷2=5050
练习3:求100+99+98+…+61+60的值
题型补充:求1 ~ 99 这99个连续自然数的所有数字之和。
分析与解答:首先应该弄清楚这题是求99个连续自然数的数字之和,而不是求这99个数之和。为了能方便地解决问题,我们不妨把0算进来(它不影响我们计算数字之和)计算0~99这100个数的数字之和。这100个数头尾两配对后每两个数的数字之和都相等,是9+9=18,一共有100÷2=50对,所以,1~99这99个连续自然数的所有数字之和是18×50=900。
练习四
1.求1~199这199个连续自然数的所有数字之和。
新定义简析:
定义新运算是指运用某种特殊符号来表示特定的意义,从而解答某些特殊算式的一种运算。
解答定义新运算,关键是要正确地理解新定义的算式含义,然后严格按照新定义的计算程序,将数值代入,转化为常规的四则运算算式进行计算。
定义新运算是一种人为的、临时性的运算形式,它使用的是一些特殊的运算符号,如:*、等,这是与四则运算中的“、、、·”不同的。
新定义的算式中有括号的,要先算括号里面的。但它在没有转化前,是不适合于各种运算定律的。
例题1:
假设a*b=(a+b)+(a-b),求13*5和13*(5*4)。
13*5=(13+5)+(13-5)=18+8=26
5*4=(5+4)+(5-4)=10
13*(5*4)=13*10=(13+10)+(13-10)=26
练习1
1..将新运算“*”定义为:a*b=(a+b)×(a-b).求27*9。
例题2:
设p、q是两个数,规定:p△q=4×q-(p+q)÷2。求3△(4△6).
3△(4△6).
=3△【4×6-(4+6)÷2】
=3△19
=4×19-(3+19)÷2
=76-11
=65
练习2:
设p、q是两个数,规定p△q=4×q-(p+q)÷2,求5△(6△4)。
例题3:
如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,4*2=4+44。那么7*4=?,210*2=?
7*4=7+77+777+7777=8638
210*2=210+210210=210420
练习3:
如果1*5=1+11+111+1111+11111,2*4=2+22+222+2222,3*3=3+33+333,…..那么,4*4=?,18*3=?
例题4:
规定②=1×2×3,③=2×3×4 ,④=3×4×5,⑤=4×5×6,……如果 EQ \F(1,⑥) - EQ \F(1,⑦) = EQ \F(1,⑦) ×A,那么A是几?
A =( EQ \F(1,⑥) - EQ \F(1,⑦) )÷ EQ \F(1,⑦)
=( EQ \F(1,⑥) - EQ \F(1,⑦) )×⑦
= EQ \F(⑦,⑥) -1
=-1
=
练习4
规定:②=1×2×3,③=2×3×4,④=3×4×5,⑤=4×5×6,……..如果 EQ \F(1,⑧) - EQ \F(1,⑨) = EQ \F(1,⑨) ×A,那么A=?。
同课章节目录
