18.2.1 矩形 课件(28张)
图片预览





文档简介
(共28张PPT)
学会学习的人,是非常幸福的人!
——米南德
18.2.1
矩
形(1)
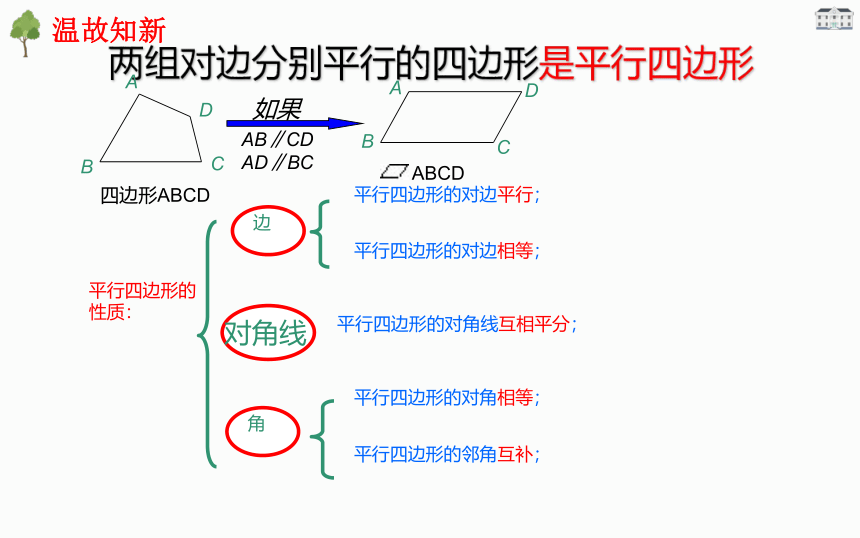
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
温故知新
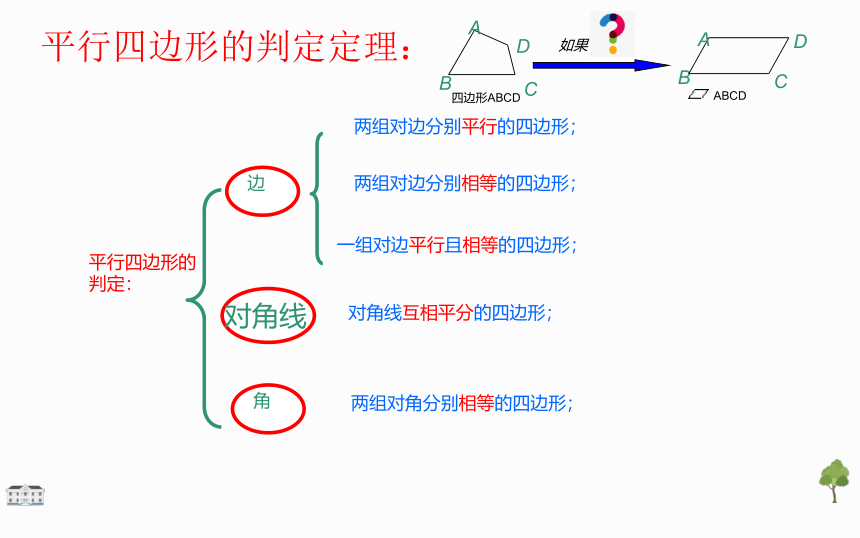
平行四边形的判定:
边
两组对边分别平行的四边形;
两组对边分别相等的四边形;
角
两组对角分别相等的四边形;
对角线
对角线互相平分的四边形;
一组对边平行且相等的四边形;
平行四边形的判定定理:
A
B
C
D
四边形ABCD
如果
B
D
ABCD
A
C
感受新知——矩形
感受新知——矩形
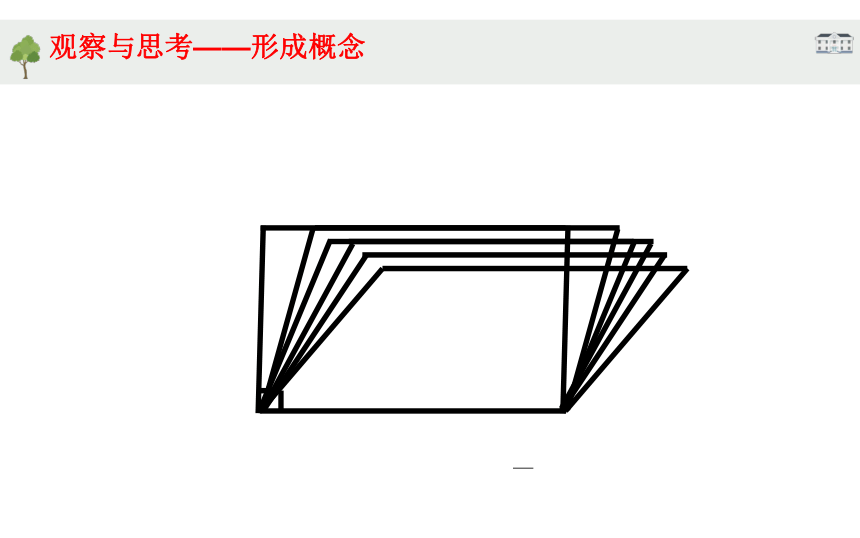
独木桥
当独木桥前后运动时,四边形ABCD是什么形状?
当独木桥最后停下时,四边形ABCD有什么特殊的变化?
当独木桥静止时,四边形ABCD是什么图形?
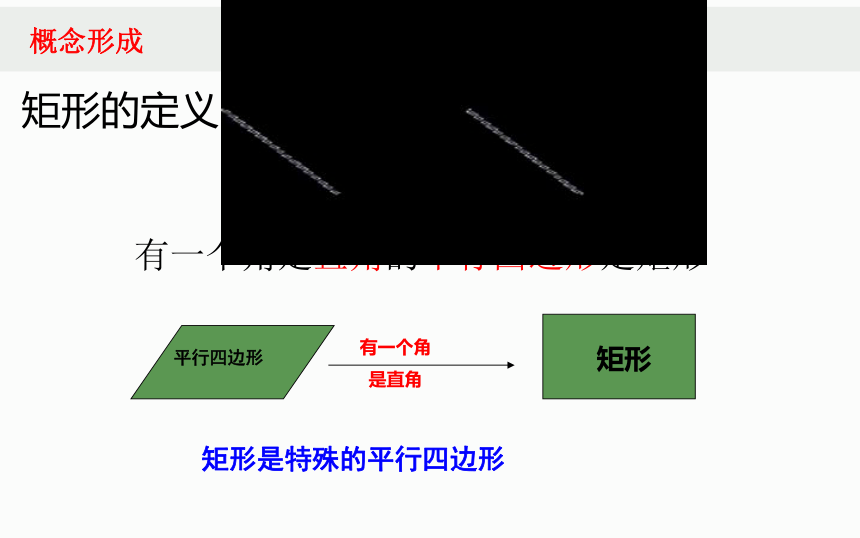
有一个角是直角
的平行四边形叫做矩
形.
小学中学习过的
长方形是矩形吗?正
方形是矩形吗?
A
B
C
D
观察与思考——形成概念
观察与思考——形成概念
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
概念形成
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:
探究新知
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
探究新知
A
B
C
D
O
合作互助——探究新知
你能证明它们吗?试着与身边的同学们一起来完成吧~~~~~~
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,
∠A=90°。
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:
∵四边形ABCD是矩形
∴
∠A=∠C
∠B
=
∠D
∠A
+∠B
=
180°
∴
∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
展示成果
已知:如图,四边形ABCD是矩形
求证:AC
=
BD
A
B
C
D
证明:∵四边形ABCD是矩形
∴∠ABC
=
∠DCB
=
90°
AB
=
DC
在△ABC与△DCB中
AB
=
DC
∠ABC
=
∠DCB
=
90°
BC
=
CB
∴△ABC≌△DCB
∴AC
=
BD
即矩形的对角线相等
求证:矩形的对角线相等
展示成果
A
B
C
D
O
角
对角线
矩形的四个角都是直角
矩形的对角线相等
矩形的特殊性质:
得到结论
矩形的
两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形
的两条对角线相等
边
对角线
角
符号语言
∵四边形ABCD是矩形
∴AD
=
BC
,CD
=
AB
∴AD
∥BC
,CD
∥AB
∴AC=
BD
∴AO=
CO
,OD
=
OB
矩形的性质
A
B
C
D
O
另外,矩形是轴对称图形吗?若是,有几条对称轴?是中心对称图形吗?若是,对称中心是什么?
矩形是轴对称图形,有四条对称抽。是中心对称图形,对称中心是对角线交点。
直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半.
例1
如图,矩形ABCD中,对角线AC、BD相交于点O,你知道OC与BD有什么关系吗?
由此,你能得到什么结论吗?
精讲实练
例2:
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
解:∵四边形ABCD是矩形
∴
OA=OB
∵∠AOB=60°
∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长
AC=BD=2OA=8(㎝)
D
C
B
A
O
AD=4cm
精讲实练
巩固新知
1、矩形具有而一般平行四边形不具有的性质是
(
)
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
2、已知:四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=_______
㎝
OB=_______
㎝
(2)若已知
∠DOC=120°,AC=8㎝,则AD=
_____cm
AB=
_____cm
5
10
4
巩固新知
O
D
C
B
A
攻关检测——第一关
矩形具有而平行四边形不具有的性质(
)
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等
D
攻关检测——第二关
下面性质中,矩形不一定具有的是(
)
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直
D
攻关检测——第三关
已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
(
)
A.50°
B.60°
C.70°
D.80°
D
攻关检测——第四关
如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
O
E
D
C
A
B
小结一下吧!
定义:
________的平行四边形叫做矩形;
特殊性质:
矩形的四个角_____________;
矩形的对角线_____________;
矩形有______条对称轴。
边
角
对角线
对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
这是矩形所特有的性质
类比更清楚!
小练习册
18.2.1矩形
第一课时
课后作业
辛苦大家了!
同学们再见!
学会学习的人,是非常幸福的人!
——米南德
18.2.1
矩
形(1)
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
温故知新
平行四边形的判定:
边
两组对边分别平行的四边形;
两组对边分别相等的四边形;
角
两组对角分别相等的四边形;
对角线
对角线互相平分的四边形;
一组对边平行且相等的四边形;
平行四边形的判定定理:
A
B
C
D
四边形ABCD
如果
B
D
ABCD
A
C
感受新知——矩形
感受新知——矩形
独木桥
当独木桥前后运动时,四边形ABCD是什么形状?
当独木桥最后停下时,四边形ABCD有什么特殊的变化?
当独木桥静止时,四边形ABCD是什么图形?
有一个角是直角
的平行四边形叫做矩
形.
小学中学习过的
长方形是矩形吗?正
方形是矩形吗?
A
B
C
D
观察与思考——形成概念
观察与思考——形成概念
有一个角是直角的平行四边形是矩形
矩形的定义:
平行四边形
矩形
有一个角
是直角
矩形是特殊的平行四边形
概念形成
具备平行四边形所有的性质
A
B
C
D
O
角
边
对角线
对边平行且相等
对角相等
对角线互相平分
矩形的一般性质:
探究新知
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想1:矩形的四个角都是直角.
猜想2:矩形的对角线相等.
探究新知
A
B
C
D
O
合作互助——探究新知
你能证明它们吗?试着与身边的同学们一起来完成吧~~~~~~
求证:矩形的四个角都是直角.
已知:如图,四边形ABCD是矩形,
∠A=90°。
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:
∵四边形ABCD是矩形
∴
∠A=∠C
∠B
=
∠D
∠A
+∠B
=
180°
∴
∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
展示成果
已知:如图,四边形ABCD是矩形
求证:AC
=
BD
A
B
C
D
证明:∵四边形ABCD是矩形
∴∠ABC
=
∠DCB
=
90°
AB
=
DC
在△ABC与△DCB中
AB
=
DC
∠ABC
=
∠DCB
=
90°
BC
=
CB
∴△ABC≌△DCB
∴AC
=
BD
即矩形的对角线相等
求证:矩形的对角线相等
展示成果
A
B
C
D
O
角
对角线
矩形的四个角都是直角
矩形的对角线相等
矩形的特殊性质:
得到结论
矩形的
两条对角线互相平分
矩形的两组对边分别平行
矩形的两组对边分别相等
矩形的四个角都是直角
矩形
的两条对角线相等
边
对角线
角
符号语言
∵四边形ABCD是矩形
∴AD
=
BC
,CD
=
AB
∴AD
∥BC
,CD
∥AB
∴AC=
BD
∴AO=
CO
,OD
=
OB
矩形的性质
A
B
C
D
O
另外,矩形是轴对称图形吗?若是,有几条对称轴?是中心对称图形吗?若是,对称中心是什么?
矩形是轴对称图形,有四条对称抽。是中心对称图形,对称中心是对角线交点。
直角三角形性质定理:
直角三角形斜边上的中线等于斜边的一半.
例1
如图,矩形ABCD中,对角线AC、BD相交于点O,你知道OC与BD有什么关系吗?
由此,你能得到什么结论吗?
精讲实练
例2:
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?
解:∵四边形ABCD是矩形
∴
OA=OB
∵∠AOB=60°
∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长
AC=BD=2OA=8(㎝)
D
C
B
A
O
AD=4cm
精讲实练
巩固新知
1、矩形具有而一般平行四边形不具有的性质是
(
)
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C
2、已知:四边形ABCD是矩形
(1)若已知AB=8㎝,AD=6㎝,
则AC=_______
㎝
OB=_______
㎝
(2)若已知
∠DOC=120°,AC=8㎝,则AD=
_____cm
AB=
_____cm
5
10
4
巩固新知
O
D
C
B
A
攻关检测——第一关
矩形具有而平行四边形不具有的性质(
)
(A)内角和是360度
(B)对角相等
(C)对边平行且相等
(D)对角线相等
D
攻关检测——第二关
下面性质中,矩形不一定具有的是(
)
(A)对角线相等
(B)四个角相等
(C)是轴对称图形
(D)对角线垂直
D
攻关检测——第三关
已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
(
)
A.50°
B.60°
C.70°
D.80°
D
攻关检测——第四关
如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
O
E
D
C
A
B
小结一下吧!
定义:
________的平行四边形叫做矩形;
特殊性质:
矩形的四个角_____________;
矩形的对角线_____________;
矩形有______条对称轴。
边
角
对角线
对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
这是矩形所特有的性质
类比更清楚!
小练习册
18.2.1矩形
第一课时
课后作业
辛苦大家了!
同学们再见!
