5.1.2垂线(1) 同步练习(含答案)
文档属性
| 名称 | 5.1.2垂线(1) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 07:40:40 | ||
图片预览




文档简介
11506200118745005.1.2垂线(1)同步练习
一、选择题
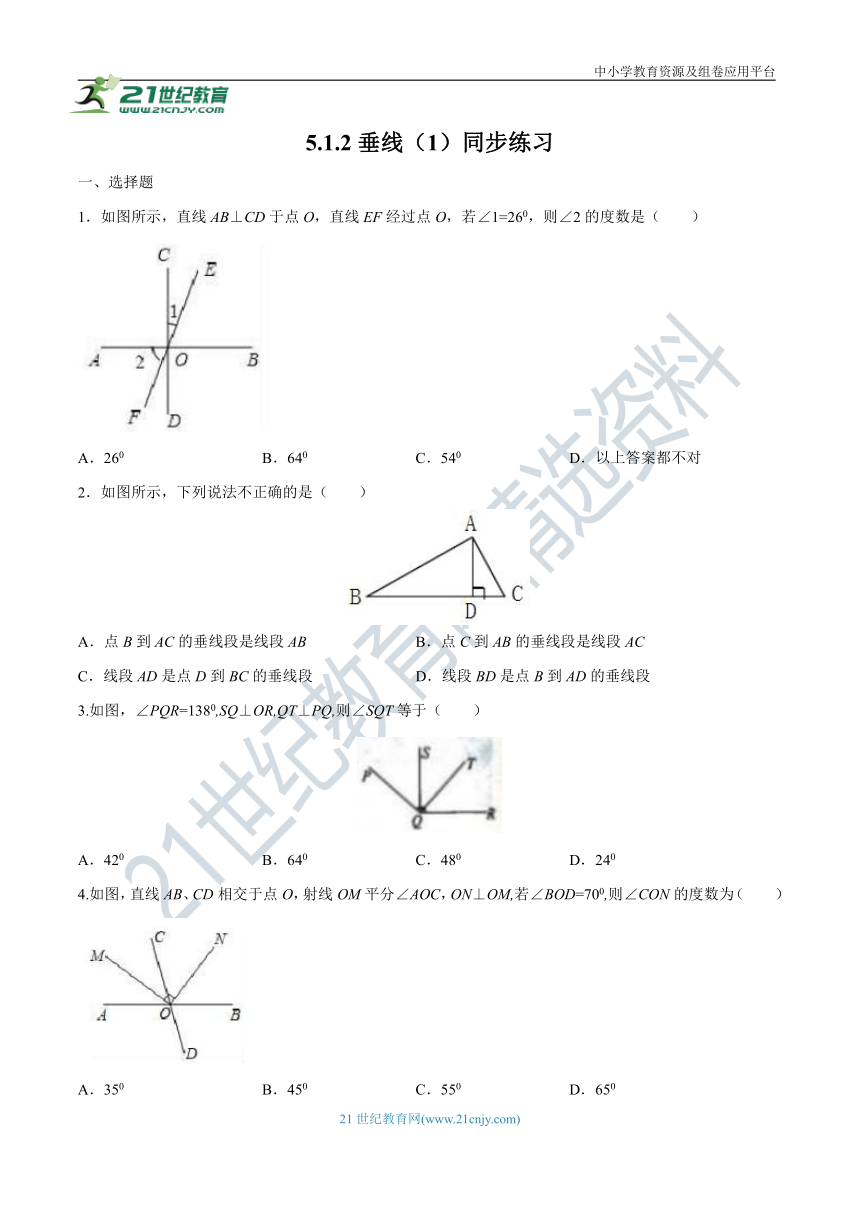
1.如图所示,直线AB⊥CD于点O,直线EF经过点O,若∠1=260,则∠2的度数是( )
A.260 B.640 C.540 D.以上答案都不对
2.如图所示,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段 D.线段BD是点B到AD的垂线段
3.如图,∠PQR=1380,SQ⊥OR,QT⊥PQ,则∠SQT等于( )
A.420 B.640 C.480 D.240
4.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠BOD=700,则∠CON的度数为( )
A.350 B.450 C.550 D.650
5.如图,直线l1与l2相交于点O,OM⊥l1,若∠α=440,则∠β等于( )
A.550 B.460 C.450 D.440
6.如图,直线AB与直线CD相交于点O,E是∠COB内一点,且OE⊥AB,∠AOC=350,则∠EOD的度数是( )
A.1550 B.1450 C.1350 D.1250
7.如图,∠AOB=1800,OD、OE分别是∠AOC和∠BOC的平分线,则与OD垂直的射线是( )
A.OA B.OC C.OE D.OB
8.如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=350,则∠DOF=()
A.650 B.450 C.350 D.550
9.如图,∠1=150,∠AOC=900,点B,O,D在同一直线上,则∠2的度数为( )
A.750 B.150 C.1050 D.1650
10.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30O时,∠BOD等于( )
A.600 B.1200 C.60O或900 D.600或1200
二填空题
11.如果CD⊥AB于D,自CD上任一点向AB作垂线,那么所画垂线均与CD重合,这是因为___________________________.
12.如图,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD=______.
13.如图,直线AB、CD、EF交于一点O,CO⊥EF且∠GOB=300,∠AOC=400,则∠COE=_____.
14.已知如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=720,则∠BOD=_____.
15.从钝角∠AOB的顶点O引射线OC⊥OA,若∠ACO:∠COB=3:1,则∠AOB=______。
16.如图,直线AB、CD相交于O,EO⊥AB,OB平分∠DOF,若∠EOC=1150,则∠BOF=____。∠COF=______.
17.如图是一把剪刀,若∠1与∠2互为余角,则∠1=______.
18.如图,OA⊥OB于O,直线CD经过点O,∠AOD=350,则∠BOC=_____
19.如图,直线AB与CD相交于点O,EO⊥AB于O,则∠1与∠2的关系是_________.
三、解答题
20.如图,已知直线AB,CD,EF相交于点O,AB⊥CD,∠DOE=1270,求∠AOF的大小。
21.如图,直线AB,CD相交于点O,OA平分∠EO C.
(1)若∠EOC=800,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数。
22.如图,已知直线AB、CD相交于点O,∠COE=900
(1)若∠AOC=360,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数。
23.在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=400时,求∠BOD的度数是多少?
24.如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC
(1)若∠BOC=500,试探究OE、OF的位置关系;
(2)若∠BOC=α(00
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
B
C
A
C
B
D
C
D
C
D
二、填空题
11.过一点,有且只有一条直线与已知直线垂直
12.600
13.200
14.360
15.1200
16.250,1300
17.450
18.1250
19.互余
三、解答题
20.解析:∵AB⊥CD,
∴∠DOB=900.
∵∠DOE=1270
∴∠BOE=∠DOE–∠DOB
=1270–900=370
∴∠AOF=∠BOE=370
21.解析:(1)∵∠EOC=800,OA平分∠EOC.
∴∠AOC=false∠EOC=400
∴∠BOD=∠AOC=400
(2)∵∠COD=1800,∠EOC=∠EOD,
∴∠EOC=∠EOD=900
∵OA平分∠EOC.
∴∠AOC=false∠EOC=450
∴∠BOD∠AOC=450
22.解析:(1)∵∠AOC+∠COE+∠BOE=1800,∠COE=900,∠AOC=360,
∴∠BOE=1800–(∠AOC+∠COE)=540
(2)∵∠BOD:∠BOC=1:5,
∴∠BOC=5∠BOD.
∵∠BOD+∠BOC=1800,
∴∠BOD+5∠BOD=1800
∴∠BOD=300,
∴∠COA=∠BOD=300.
∵∠AOE=∠COA+∠COE,∠COE=900,
∴∠AOE=1200
23.解析:当OC、OD在直线AB的同侧时,如图
∵OC⊥OD
∴∠COD=900,
∵∠AOC=400
∴∠BOD=1800–900–400=500.
当OC、OD在直线AB的异侧时,如图
∵OC⊥OD
∴∠COD=900,
∵∠AOC=400,
∴∠AOD=500
∴∠BOD=1800–500=1300
综上∠BOD的度数是500或1300
24.解析:(1)OE⊥OF
由邻补角定义,可得∠AOC=1800–∠BOC=1300
由OE平分∠AOC,OF平分∠BOC可得∠COF=false∠BOC=250,∠COE=false∠AOC=650
所以∠EOF=∠COF+∠COE=900.
(2) OE⊥OF仍成立。
∵∠AOC=1800–α,∠COF=falseα,
∴∠COE=false(1800–α)=900–falseα,
∴∠EOF=∠COF+∠COE=falseα+(900–falseα)=900
由此发现:无论∠BOF度数是多少,∠EOF总等于900。即邻补角的平分线互相垂直
一、选择题
1.如图所示,直线AB⊥CD于点O,直线EF经过点O,若∠1=260,则∠2的度数是( )
A.260 B.640 C.540 D.以上答案都不对
2.如图所示,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB B.点C到AB的垂线段是线段AC
C.线段AD是点D到BC的垂线段 D.线段BD是点B到AD的垂线段
3.如图,∠PQR=1380,SQ⊥OR,QT⊥PQ,则∠SQT等于( )
A.420 B.640 C.480 D.240
4.如图,直线AB、CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠BOD=700,则∠CON的度数为( )
A.350 B.450 C.550 D.650
5.如图,直线l1与l2相交于点O,OM⊥l1,若∠α=440,则∠β等于( )
A.550 B.460 C.450 D.440
6.如图,直线AB与直线CD相交于点O,E是∠COB内一点,且OE⊥AB,∠AOC=350,则∠EOD的度数是( )
A.1550 B.1450 C.1350 D.1250
7.如图,∠AOB=1800,OD、OE分别是∠AOC和∠BOC的平分线,则与OD垂直的射线是( )
A.OA B.OC C.OE D.OB
8.如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=350,则∠DOF=()
A.650 B.450 C.350 D.550
9.如图,∠1=150,∠AOC=900,点B,O,D在同一直线上,则∠2的度数为( )
A.750 B.150 C.1050 D.1650
10.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30O时,∠BOD等于( )
A.600 B.1200 C.60O或900 D.600或1200
二填空题
11.如果CD⊥AB于D,自CD上任一点向AB作垂线,那么所画垂线均与CD重合,这是因为___________________________.
12.如图,AO⊥BO,O为垂足,直线CD过点O,且∠BOD=2∠AOC,则∠BOD=______.
13.如图,直线AB、CD、EF交于一点O,CO⊥EF且∠GOB=300,∠AOC=400,则∠COE=_____.
14.已知如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=720,则∠BOD=_____.
15.从钝角∠AOB的顶点O引射线OC⊥OA,若∠ACO:∠COB=3:1,则∠AOB=______。
16.如图,直线AB、CD相交于O,EO⊥AB,OB平分∠DOF,若∠EOC=1150,则∠BOF=____。∠COF=______.
17.如图是一把剪刀,若∠1与∠2互为余角,则∠1=______.
18.如图,OA⊥OB于O,直线CD经过点O,∠AOD=350,则∠BOC=_____
19.如图,直线AB与CD相交于点O,EO⊥AB于O,则∠1与∠2的关系是_________.
三、解答题
20.如图,已知直线AB,CD,EF相交于点O,AB⊥CD,∠DOE=1270,求∠AOF的大小。
21.如图,直线AB,CD相交于点O,OA平分∠EO C.
(1)若∠EOC=800,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数。
22.如图,已知直线AB、CD相交于点O,∠COE=900
(1)若∠AOC=360,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数。
23.在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,当∠AOC=400时,求∠BOD的度数是多少?
24.如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC
(1)若∠BOC=500,试探究OE、OF的位置关系;
(2)若∠BOC=α(00
参考答案
一、选择题
1
2
3
4
5
6
7
8
9
10
B
C
A
C
B
D
C
D
C
D
二、填空题
11.过一点,有且只有一条直线与已知直线垂直
12.600
13.200
14.360
15.1200
16.250,1300
17.450
18.1250
19.互余
三、解答题
20.解析:∵AB⊥CD,
∴∠DOB=900.
∵∠DOE=1270
∴∠BOE=∠DOE–∠DOB
=1270–900=370
∴∠AOF=∠BOE=370
21.解析:(1)∵∠EOC=800,OA平分∠EOC.
∴∠AOC=false∠EOC=400
∴∠BOD=∠AOC=400
(2)∵∠COD=1800,∠EOC=∠EOD,
∴∠EOC=∠EOD=900
∵OA平分∠EOC.
∴∠AOC=false∠EOC=450
∴∠BOD∠AOC=450
22.解析:(1)∵∠AOC+∠COE+∠BOE=1800,∠COE=900,∠AOC=360,
∴∠BOE=1800–(∠AOC+∠COE)=540
(2)∵∠BOD:∠BOC=1:5,
∴∠BOC=5∠BOD.
∵∠BOD+∠BOC=1800,
∴∠BOD+5∠BOD=1800
∴∠BOD=300,
∴∠COA=∠BOD=300.
∵∠AOE=∠COA+∠COE,∠COE=900,
∴∠AOE=1200
23.解析:当OC、OD在直线AB的同侧时,如图
∵OC⊥OD
∴∠COD=900,
∵∠AOC=400
∴∠BOD=1800–900–400=500.
当OC、OD在直线AB的异侧时,如图
∵OC⊥OD
∴∠COD=900,
∵∠AOC=400,
∴∠AOD=500
∴∠BOD=1800–500=1300
综上∠BOD的度数是500或1300
24.解析:(1)OE⊥OF
由邻补角定义,可得∠AOC=1800–∠BOC=1300
由OE平分∠AOC,OF平分∠BOC可得∠COF=false∠BOC=250,∠COE=false∠AOC=650
所以∠EOF=∠COF+∠COE=900.
(2) OE⊥OF仍成立。
∵∠AOC=1800–α,∠COF=falseα,
∴∠COE=false(1800–α)=900–falseα,
∴∠EOF=∠COF+∠COE=falseα+(900–falseα)=900
由此发现:无论∠BOF度数是多少,∠EOF总等于900。即邻补角的平分线互相垂直
