2020-2021学年高二下学期数学人教A版选修2-2第三章3.2 复数的四则运算(加减乘除)课件(共22张PPT)
文档属性
| 名称 | 2020-2021学年高二下学期数学人教A版选修2-2第三章3.2 复数的四则运算(加减乘除)课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 22:04:16 | ||
图片预览








文档简介
(共22张PPT)
3.2
复数代数形式的四则运算
复习回顾
复数
z=a+bi
(a,b∈R)
(a,b)
一
一对应
点
复数
z=a+bi
(a,b∈R)
一
一对应
复数的几何意义
复数的模
复数
z=a+bi
(a,b∈R)的模是
一、复数的加减法
?
?
?
(a+c)
(b+d)
(a-c)
(b-d)
运算律:
交换律:
结合律:
例1
复数的加减法运算
(1)计算:(5-6i)+(-2-i)-(3+4i);
(2)设z1=x+2i,z2=3-yi(x,y∈R),
且z1+z2=5-6i,求z1-z2.
跟踪训练
复数的加减法运算
复数(1+2i)+(3-4i)-(-5-3i)对应的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
复数的加减法的几何意义
复数加法:
向量加法:
O
Z
?
二、复数的加减法的几何意义
复数减法:
向量减法:
O
Z
?
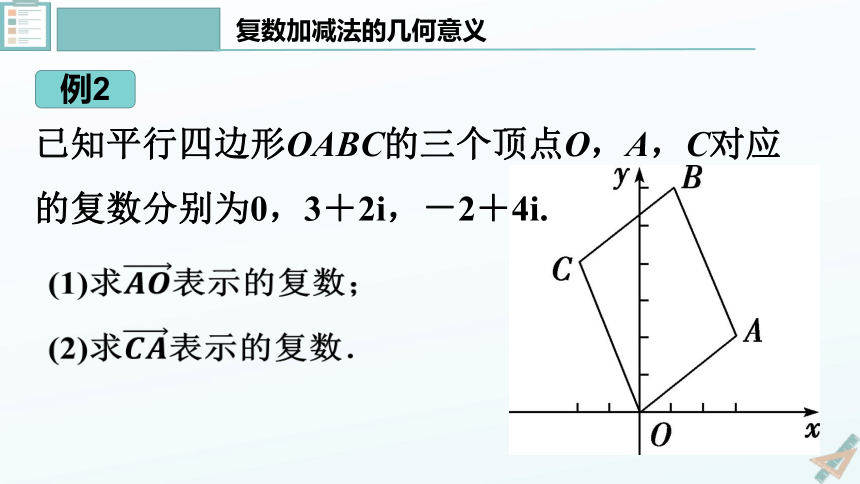
例2
复数加减法的几何意义
已知平行四边形OABC的三个顶点O,A,C对应的复数分别为0,3+2i,-2+4i.
?
?
跟踪训练
A
复数与复平面内的向量
三、复数代数形式的乘法
(1)复数的乘法法则
设z1=a+bi,z2=c+di(a,b,c,d∈R),
则z1·z2=(a+bi)(c+di)=__________________.
三、复数代数形式的乘法
三、复数代数形式的乘法
四、共轭复数
(1)如果两个复数满足实部_____,虚部___________时,称这两个复数互为共轭复数.z的共轭复数用
表示,
即z=a+bi(a,b∈R),则
=__________.
(2)复数与共轭复数的乘法性质
z=(a+bi)(a-bi)=
相等
互为相反数
a-bi
a2+b2
实数
例3
共轭复数
C
跟踪训练
共轭复数
五、复数代数形式的除法
设z1=a+bi,z2=c+di
(z2≠0)(a,b,c,d∈R),
例1
复数代数形式的乘除运算
跟踪训练
D
复数代数形式的乘除运算
跟踪训练
复数代数形式的乘除运算
六、i
的周期性
1
2
0
例2
i
的运算性质
请记住
跟踪训练
i
的运算性质
B
-i
3.2
复数代数形式的四则运算
复习回顾
复数
z=a+bi
(a,b∈R)
(a,b)
一
一对应
点
复数
z=a+bi
(a,b∈R)
一
一对应
复数的几何意义
复数的模
复数
z=a+bi
(a,b∈R)的模是
一、复数的加减法
?
?
?
(a+c)
(b+d)
(a-c)
(b-d)
运算律:
交换律:
结合律:
例1
复数的加减法运算
(1)计算:(5-6i)+(-2-i)-(3+4i);
(2)设z1=x+2i,z2=3-yi(x,y∈R),
且z1+z2=5-6i,求z1-z2.
跟踪训练
复数的加减法运算
复数(1+2i)+(3-4i)-(-5-3i)对应的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
A
复数的加减法的几何意义
复数加法:
向量加法:
O
Z
?
二、复数的加减法的几何意义
复数减法:
向量减法:
O
Z
?
例2
复数加减法的几何意义
已知平行四边形OABC的三个顶点O,A,C对应的复数分别为0,3+2i,-2+4i.
?
?
跟踪训练
A
复数与复平面内的向量
三、复数代数形式的乘法
(1)复数的乘法法则
设z1=a+bi,z2=c+di(a,b,c,d∈R),
则z1·z2=(a+bi)(c+di)=__________________.
三、复数代数形式的乘法
三、复数代数形式的乘法
四、共轭复数
(1)如果两个复数满足实部_____,虚部___________时,称这两个复数互为共轭复数.z的共轭复数用
表示,
即z=a+bi(a,b∈R),则
=__________.
(2)复数与共轭复数的乘法性质
z=(a+bi)(a-bi)=
相等
互为相反数
a-bi
a2+b2
实数
例3
共轭复数
C
跟踪训练
共轭复数
五、复数代数形式的除法
设z1=a+bi,z2=c+di
(z2≠0)(a,b,c,d∈R),
例1
复数代数形式的乘除运算
跟踪训练
D
复数代数形式的乘除运算
跟踪训练
复数代数形式的乘除运算
六、i
的周期性
1
2
0
例2
i
的运算性质
请记住
跟踪训练
i
的运算性质
B
-i
