2020-2021学年高二下学期数学人教A版选修2-3第一章1.2.2 组合与组合数课件(共22张PPT)
文档属性
| 名称 | 2020-2021学年高二下学期数学人教A版选修2-3第一章1.2.2 组合与组合数课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
1.2
排列与组合
1.2.2
组合与组合数
(1)从1,2,3三个数字中取出两个不同数字组成两位数,这样的两位数共有多少个?
(2)从1,2,3三个数字中取出两个不同数字组成集合,能构成多少个不同的集合?
思考1:它们的结果相同吗?
思考2:它们是排列问题吗?
思考3:它们有什么异同点?
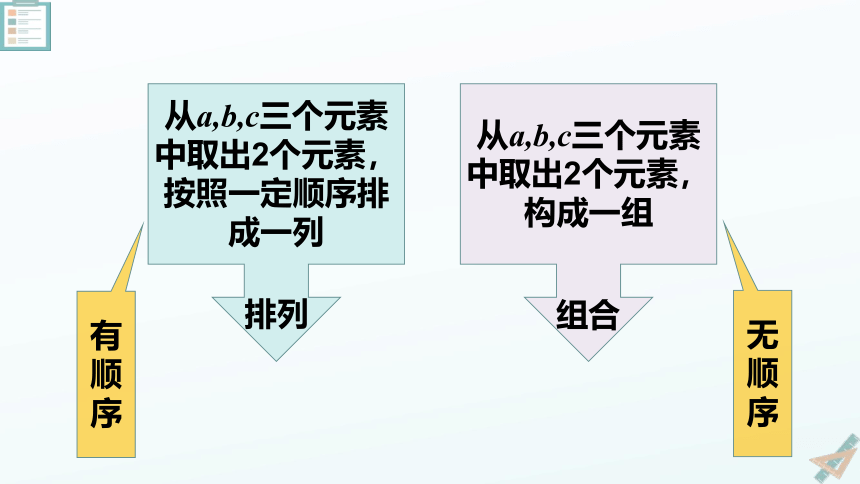
从a,b,c三个元素中取出2个元素,按照一定顺序排成一列
从a,b,c三个元素中取出2个元素,构成一组
排列
组合
有顺序
无顺序
1.组合的概念
组合:从n个不同的元素中取出m(m≤n)个元素,
合成一组
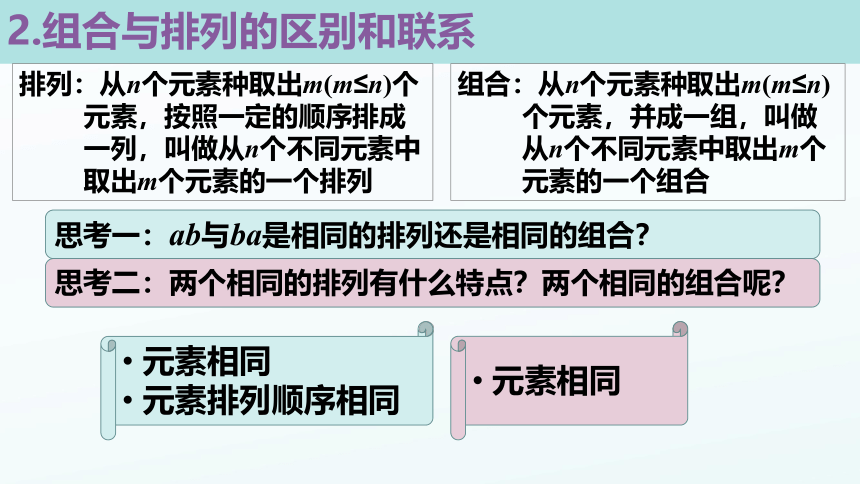
2.组合与排列的区别和联系
排列:从n个元素种取出m(m≤n)个
元素,按照一定的顺序排成
一列,叫做从n个不同元素中
取出m个元素的一个排列
组合:从n个元素种取出m(m≤n)
个元素,并成一组,叫做
从n个不同元素中取出m个
元素的一个组合
思考一:ab与ba是相同的排列还是相同的组合?
思考二:两个相同的排列有什么特点?两个相同的组合呢?
元素相同
元素排列顺序相同
元素相同
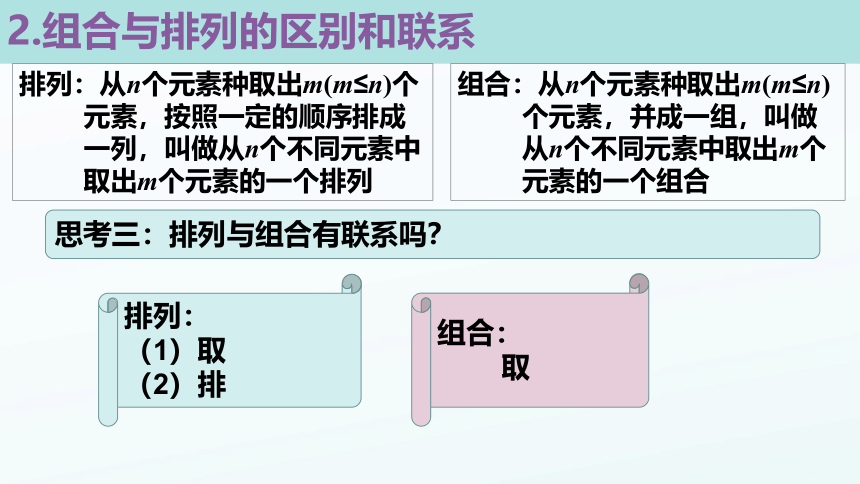
2.组合与排列的区别和联系
排列:从n个元素种取出m(m≤n)个
元素,按照一定的顺序排成
一列,叫做从n个不同元素中
取出m个元素的一个排列
组合:从n个元素种取出m(m≤n)
个元素,并成一组,叫做
从n个不同元素中取出m个
元素的一个组合
思考三:排列与组合有联系吗?
排列:
(1)取
(2)排
组合:
取
3.组合数
组合数:从n个不同的元素中取出m(m≤n)个元素的
所有不同组合的个数叫做从n个不同元素中取出
m个元素的组合数,用
表示.
4.组合数的性质
性质1:
性质2:
规定:
例1
组合概念的理解
判断下列问题是组合问题还是排列问题:
(1)把5本不同的书分给5个学生,每人一本;
(2)从7本不同的书中取出5本给某个同学;
(3)10个人互相写一封信,共写了几封信;
(4)10个人互相通一次电话,共通了几次电话.
判断下列问题是排列问题,还是组合问题.
(1)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个?
(2)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个?
(3)从a,b,c,d四名学生中选两名去完成同一份工作,有多少种不同的选法?
跟踪训练
组合概念的理解
例2
组合数公式、性质的应用
计算下列各式的值
跟踪训练
组合数公式、性质的应用
1.解方程:
跟踪训练
组合数公式、性质的应用
2.证明:
判断正误(正确的打“√”,错误的打“×”)
(1)从a1,a2,a3三个不同元素中任取两个元素组成一个组合,所有组合的个数为
.( )
(2)从1,3,5,7中任取两个数相乘可得
个积.( )
(3)
=5×4×3=60.
( )
(4)
=
=2
017.
( )
自我检测
1
若
=10,则n的值为( )
A.10
B.5
C.3
D.4
自我检测
2
B
从9名学生中选出3名参加“希望英语”口语比赛,不同选法有( )
A.504种
B.729种
C.84种
D.27种
自我检测
3
C
4
210
自我检测
5
18
有4名男医生、3名女医生,从中选出2名男医生、1名女医生组成1个医疗小组,则不同的选法共有________种.
例3
简单的组合问题
现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名去参加会议有多少种不同的选法?
(2)选出2名男教师或2名女教师参加会议,有多少种不同的选法?
(3)现要从中选出男、女教师各2名去参加会议,有多少种不同的选法?
变式
简单的组合问题
[变问法]本例其他条件不变,问题变为从中选2名教师参加会议,至少有1名男教师的选法是多少?最多有1名男教师的选法又是多少?
跟踪训练
简单的组合问题
1.在100件产品中,有98件合格品,2件次品,从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
跟踪训练
2.由13个人组成的课外活动小组,其中5个人只会跳舞,5个人只会唱歌,3个人既会唱歌也会跳舞,若从中选出4个会跳舞和4个会唱歌的人去演节目,共有多少种不同的选法?
简单的组合问题
1.2
排列与组合
1.2.2
组合与组合数
(1)从1,2,3三个数字中取出两个不同数字组成两位数,这样的两位数共有多少个?
(2)从1,2,3三个数字中取出两个不同数字组成集合,能构成多少个不同的集合?
思考1:它们的结果相同吗?
思考2:它们是排列问题吗?
思考3:它们有什么异同点?
从a,b,c三个元素中取出2个元素,按照一定顺序排成一列
从a,b,c三个元素中取出2个元素,构成一组
排列
组合
有顺序
无顺序
1.组合的概念
组合:从n个不同的元素中取出m(m≤n)个元素,
合成一组
2.组合与排列的区别和联系
排列:从n个元素种取出m(m≤n)个
元素,按照一定的顺序排成
一列,叫做从n个不同元素中
取出m个元素的一个排列
组合:从n个元素种取出m(m≤n)
个元素,并成一组,叫做
从n个不同元素中取出m个
元素的一个组合
思考一:ab与ba是相同的排列还是相同的组合?
思考二:两个相同的排列有什么特点?两个相同的组合呢?
元素相同
元素排列顺序相同
元素相同
2.组合与排列的区别和联系
排列:从n个元素种取出m(m≤n)个
元素,按照一定的顺序排成
一列,叫做从n个不同元素中
取出m个元素的一个排列
组合:从n个元素种取出m(m≤n)
个元素,并成一组,叫做
从n个不同元素中取出m个
元素的一个组合
思考三:排列与组合有联系吗?
排列:
(1)取
(2)排
组合:
取
3.组合数
组合数:从n个不同的元素中取出m(m≤n)个元素的
所有不同组合的个数叫做从n个不同元素中取出
m个元素的组合数,用
表示.
4.组合数的性质
性质1:
性质2:
规定:
例1
组合概念的理解
判断下列问题是组合问题还是排列问题:
(1)把5本不同的书分给5个学生,每人一本;
(2)从7本不同的书中取出5本给某个同学;
(3)10个人互相写一封信,共写了几封信;
(4)10个人互相通一次电话,共通了几次电话.
判断下列问题是排列问题,还是组合问题.
(1)从1,2,3,…,9九个数字中任取3个,组成一个三位数,这样的三位数共有多少个?
(2)从1,2,3,…,9九个数字中任取3个,然后把这三个数字相加得到一个和,这样的和共有多少个?
(3)从a,b,c,d四名学生中选两名去完成同一份工作,有多少种不同的选法?
跟踪训练
组合概念的理解
例2
组合数公式、性质的应用
计算下列各式的值
跟踪训练
组合数公式、性质的应用
1.解方程:
跟踪训练
组合数公式、性质的应用
2.证明:
判断正误(正确的打“√”,错误的打“×”)
(1)从a1,a2,a3三个不同元素中任取两个元素组成一个组合,所有组合的个数为
.( )
(2)从1,3,5,7中任取两个数相乘可得
个积.( )
(3)
=5×4×3=60.
( )
(4)
=
=2
017.
( )
自我检测
1
若
=10,则n的值为( )
A.10
B.5
C.3
D.4
自我检测
2
B
从9名学生中选出3名参加“希望英语”口语比赛,不同选法有( )
A.504种
B.729种
C.84种
D.27种
自我检测
3
C
4
210
自我检测
5
18
有4名男医生、3名女医生,从中选出2名男医生、1名女医生组成1个医疗小组,则不同的选法共有________种.
例3
简单的组合问题
现有10名教师,其中男教师6名,女教师4名.
(1)现要从中选2名去参加会议有多少种不同的选法?
(2)选出2名男教师或2名女教师参加会议,有多少种不同的选法?
(3)现要从中选出男、女教师各2名去参加会议,有多少种不同的选法?
变式
简单的组合问题
[变问法]本例其他条件不变,问题变为从中选2名教师参加会议,至少有1名男教师的选法是多少?最多有1名男教师的选法又是多少?
跟踪训练
简单的组合问题
1.在100件产品中,有98件合格品,2件次品,从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
跟踪训练
2.由13个人组成的课外活动小组,其中5个人只会跳舞,5个人只会唱歌,3个人既会唱歌也会跳舞,若从中选出4个会跳舞和4个会唱歌的人去演节目,共有多少种不同的选法?
简单的组合问题
