2020-2021学年八年级下册数学湘教新版第3章 图形与坐标单元测试题(Word版含答案)
文档属性
| 名称 | 2020-2021学年八年级下册数学湘教新版第3章 图形与坐标单元测试题(Word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 00:00:00 | ||
图片预览


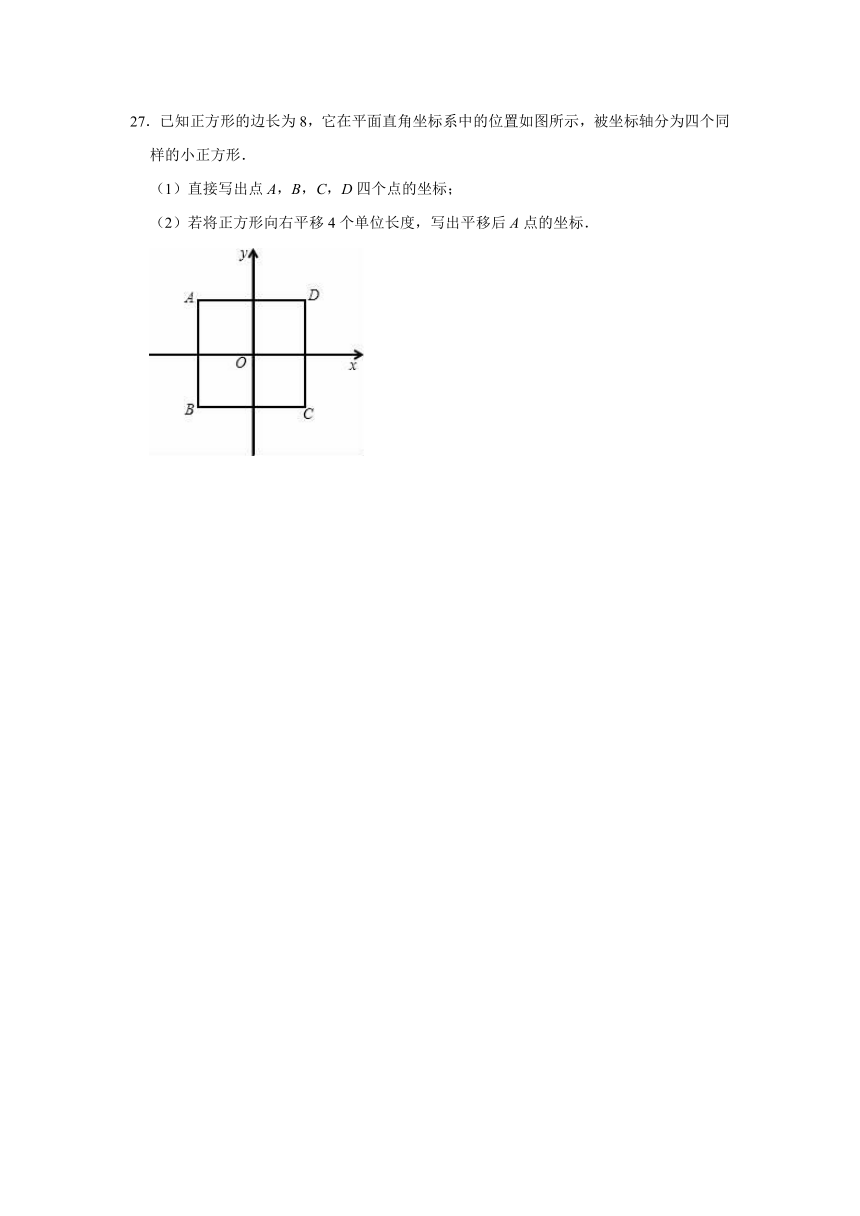
文档简介
2020-2021学年八年级下册数学湘教新版《第3章
图形与坐标》单元测试题
一.选择题
1.在平面直角坐标系中有M,N两点,若以N点为原点建立直角坐标系,则点M的坐标为(3,5),若以M点为原点建立直角坐标系,则点N的坐标是( )
A.(﹣3,5)
B.(3,﹣5)
C.(﹣3,﹣5)
D.(3,5)
2.点M(2,3),N(﹣2,4),则MN应为( )
A.17
B.1
C.
D.
3.已知点A(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,则a=( )
A.a=0
B.a=﹣9
C.a=﹣9或a=
D.a=
4.下列关于A,B两点的说法中,正确的个数是( )
①如果点A与点B关于y轴对称,则它们的纵坐标相同
②如果点A与点B的纵坐标相同,则它们关于y轴对称
③如果点A与点B的横坐标相同,则它们关于x轴对称
④如果点A与点B关于x轴对称,则它们的横坐标相同
A.1个
B.2个
C.3个
D.4个
5.如果把点A(﹣1,4)向右平移2个单位长度,再向上平移3个单位长度,则平移后的坐标是( )
A.(1,7)
B.(﹣1,7)
C.(1,﹣7)
D.(﹣1,﹣7)
6.如图,一个动点P在平面直角坐标系中按箭头所示方向做折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),…,按这样的运动规律,经过第2013次运动后,动点P的坐标是( )
A.(2012,1)
B.(2012,2)
C.(2013,1)
D.(2013,2)
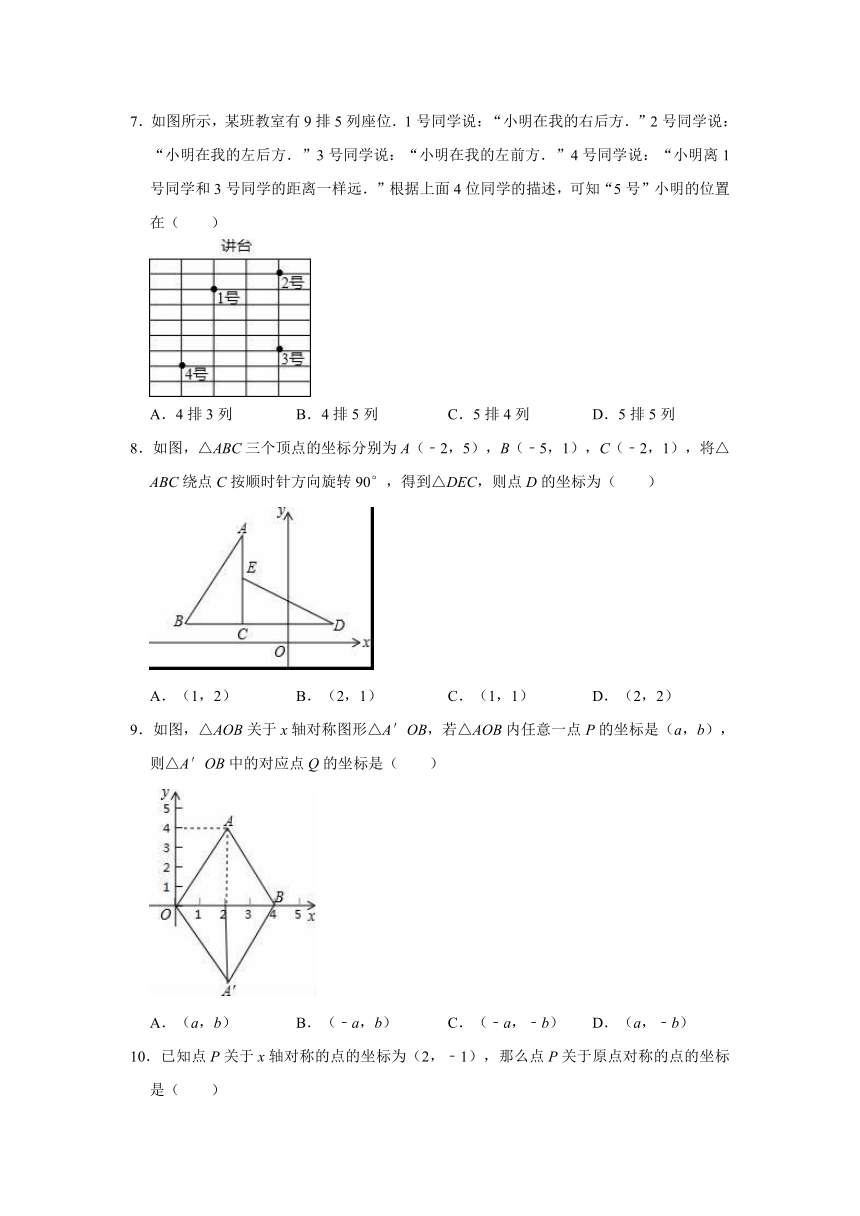
7.如图所示,某班教室有9排5列座位.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”根据上面4位同学的描述,可知“5号”小明的位置在( )
A.4排3列
B.4排5列
C.5排4列
D.5排5列
8.如图,△ABC三个顶点的坐标分别为A(﹣2,5),B(﹣5,1),C(﹣2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )
A.(1,2)
B.(2,1)
C.(1,1)
D.(2,2)
9.如图,△AOB关于x轴对称图形△A′OB,若△AOB内任意一点P的坐标是(a,b),则△A′OB中的对应点Q的坐标是( )
A.(a,b)
B.(﹣a,b)
C.(﹣a,﹣b)
D.(a,﹣b)
10.已知点P关于x轴对称的点的坐标为(2,﹣1),那么点P关于原点对称的点的坐标是( )
A.(1,﹣2)
B.(2,1)
C.(﹣2,﹣1)
D.(﹣2,1)
二.填空题
11.若点A(a,b)在第三象限,则点C(﹣a,b﹣5)在第
象限.
12.点P(1,2)关于点Q(﹣1,1)的对称点的坐标为
.
13.已知点P(﹣2,3)和点Q(2,﹣3),则P,Q两个点的位置关系是
.
14.已知点P(a,5)与Q(2,b)是关于x轴对称,则a=
,b=
.
15.在坐标平面内,已知点M(1,2)和点N(1,﹣4),那么线段MN的长为
个单位长度,MN中点的坐标为
.
16.两点(3,﹣4)、(5,a)间的距离是2,则a的值为
.
17.点M(﹣3,5)关于直线x=1对称的点M′的坐标为
.
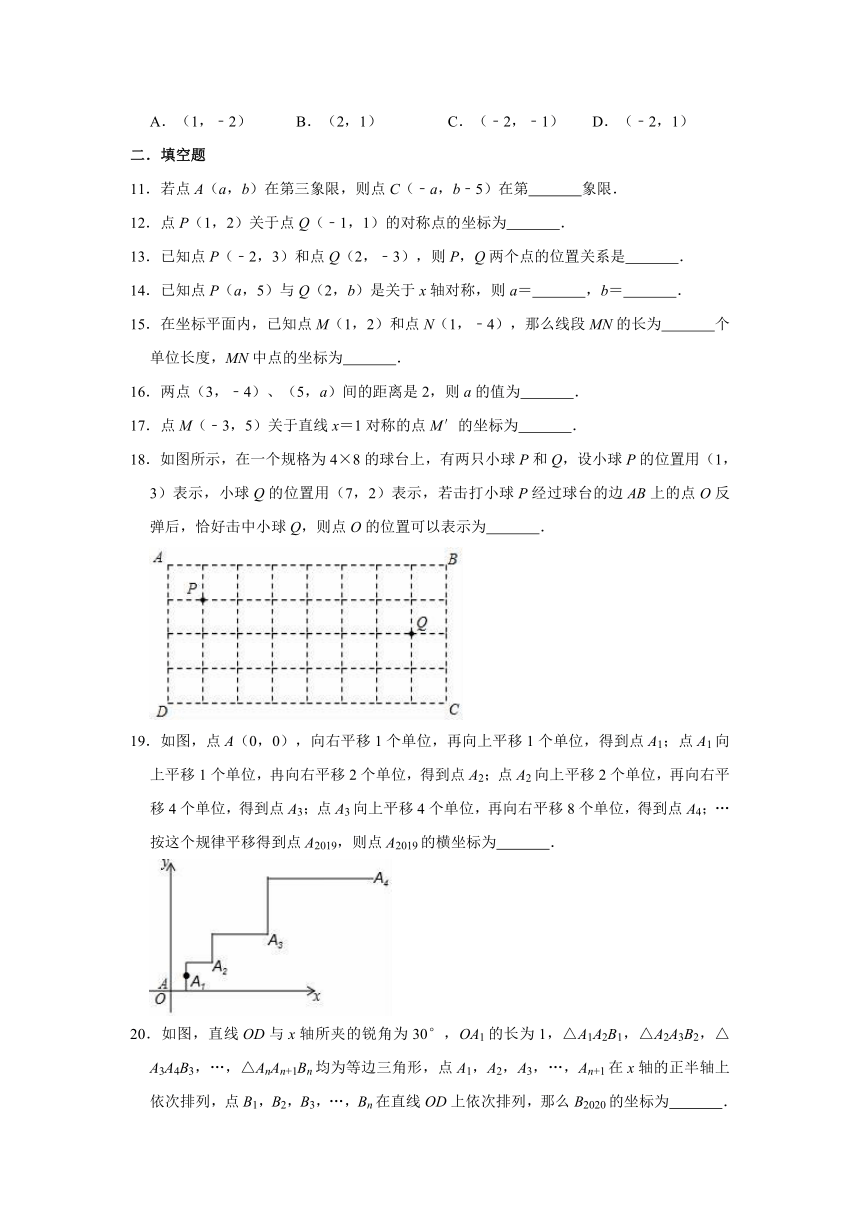
18.如图所示,在一个规格为4×8的球台上,有两只小球P和Q,设小球P的位置用(1,3)表示,小球Q的位置用(7,2)表示,若击打小球P经过球台的边AB上的点O反弹后,恰好击中小球Q,则点O的位置可以表示为
.
19.如图,点A(0,0),向右平移1个单位,再向上平移1个单位,得到点A1;点A1向上平移1个单位,冉向右平移2个单位,得到点A2;点A2向上平移2个单位,再向右平移4个单位,得到点A3;点A3向上平移4个单位,再向右平移8个单位,得到点A4;…按这个规律平移得到点A2019,则点A2019的横坐标为
.
20.如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1,△A2A3B2,△A3A4B3,…,△AnAn+1Bn均为等边三角形,点A1,A2,A3,…,An+1在x轴的正半轴上依次排列,点B1,B2,B3,…,Bn在直线OD上依次排列,那么B2020的坐标为
.
三.解答题
21.已知点P(m+3,2m﹣1),试分别根据下列条件求出点P的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到x轴的距离为2,且在第四象限.
22.小明和小东在沙滩上玩游戏,他们都从某一点出发,小明先是沿正东方向行走50米,然后沿正北方向走30米到达点A处;小东则是先沿正西方向行走20米,然后沿正南行走40米到达点B出,请问此时小明和小东相距大约多少米?
23.在平行四边形ABCD中,AB=3,BC=4,∠A=60°,建立适当的平面直角坐标系,把平行四边形ABCD的各个顶点的坐标写出来.(要求写出一组坐标即可)
24.已知点M(4p,4q+p)和点N(5﹣3q,2p﹣2)关于x轴对称,求P和Q的值,若M,N关于y轴对称呢?关于原点对称呢?
25.当m为何值时,点P(3m﹣1,m﹣2)到y轴的距离是到x轴距离的3倍?求出此时点P到原点的距离.
26.在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),求点B′的横坐标.
27.已知正方形的边长为8,它在平面直角坐标系中的位置如图所示,被坐标轴分为四个同样的小正方形.
(1)直接写出点A,B,C,D四个点的坐标;
(2)若将正方形向右平移4个单位长度,写出平移后A点的坐标.
参考答案与试题解析
一.选择题
1.解:以N点为原点建立直角坐标系,则点M的坐标为(3,5),
则以M点为原点建立直角坐标系(两直角坐标系x轴,y轴方向一致),N点的坐标是(﹣3,﹣5).
故选:C.
2.解:MN==.故选C.
3.解:∵点A(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,
∴5a﹣7=﹣(﹣6a﹣2),
解得a=﹣9.
故选:B.
4.解:正确的是:①如果点A与点B关于y轴对称,则它们的纵坐标相同;
④如果点A与点B关于x轴对称,则它们的横坐标相同;
故正确的有两个;
故选:B.
5.解:A(﹣1,4)向右平移2个单位长度得到:(﹣1+2,4),
即:(1,4),
再向上平移3个单位长度得到:(1,4+3),
即:(1,7),
故选:A.
6.解:∵第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),
第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),…,
∴按这样的运动规律,第几次横坐标即为几,纵坐标为:1,0,2,0,1,0,2,0…4个一循环,
∵=503…1,
∴经过第2013次运动后,动点P的坐标是:(2013,1).
故选:C.
7.解:根据1号同学,2号同学,3号同学的说法,可知小明在第4列,再根据4号同学说:“小明离1号同学和3号同学的距离一样远”可得小明在第5排第4列.
故选:C.
8.解:∵A(﹣2,5),B(﹣5,1),C(﹣2,1),
∴AC=4,AC∥y轴,
∵△ABC绕点C按顺时针方向旋转90°,得到△DEC,
∴∠DCE=∠ACB=90°,CD=AC=4,
∴B,C,D三点在一条直线上,
∴D(2,1),
故选:B.
9.解:∵△AOB与△A'OB关于x轴对称,
∴点P(a,b)关于x轴的对称点为(a,﹣b),
∴点P的对应点Q的坐标是(a,﹣b).
故选:D.
10.解:根据轴对称的性质,得P点的坐标是(2,1).
再根据中心对称的性质,得点P关于原点对称的点的坐标是(﹣2,﹣1).
故选:C.
二.填空题
11.解:∵点A(a,b)在第三象限,
∴a<0,b<0,
∴﹣a>0,b﹣5<0,
∴点C(﹣a,b﹣5)在第四象限.
故答案为:四.
12.解:设点P(1,2)关于点Q(﹣1,1)的对称点的坐标为(a,b),
则=﹣1,=1,
解得:a=﹣3,b=0,
∴点P(1,2)关于点Q(﹣1,1)的对称点的坐标为(﹣3,0),
故答案为:(﹣3,0).
13.解:∵P,Q两个点的横纵坐标都互为相反数,∴P,Q两个点关于原点对称,
故答案为关于原点对称.
14.解:∵点P(a,5)与Q(2,b)是关于x轴对称,
∴a=2,b=﹣5,
故答案为:2,﹣5.
15.解:∵点M(1,2)和点N(1,﹣4)横坐标相等,
∴MN∥y轴,MN=2﹣(﹣4)=6,
MN中点的坐标为(1,),即(1,﹣1).
故答案填:6、(1,﹣1).
16.解:根据题意得=2,
解得a=﹣4.
故答案为﹣4.
17.解:∵点M(﹣3,5)与点N关于直线x=1对称,
而1×2﹣(﹣3)=5,
∴点M(﹣3,5)关于直线x=1对称的点N的坐标是(5,5),
故答案为(5,5).
18.解:如图所示,
O点的坐标为(3,4),
故答案为(3,4).
19.解:点A1的横坐标为1=21﹣1,点A2的横坐为标3=22﹣1,点A3:的横坐标为7=23﹣1,点A4的横坐标为15=24﹣1,
按这个规律平移得到点An为2n﹣1,
∴点A2018的横坐标为22019﹣1,
故答案为:22019﹣1.
20.解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠B1OA2=30°,
∴∠B1OA2=∠A1B1O=30°,
∴OA2=2OA1=2,
同理可得,OAn=2n﹣1,
∵∠BnOAn+1=30°,∠BnAnAn+1=60°,
∴∠BnOAn+1=∠OBnAn=30°,
∴BnAn=OAn=2n﹣1,
即△AnBnAn+1的边长为2n﹣1,
则可求得其高为×2n﹣1=×2n﹣2,
∴点Bn的横坐标为×2n﹣1+2n﹣1=×2n﹣1=3×2n﹣2,
∴点Bn的坐标为(3×2n﹣2,×2n﹣2),
∴点B2020的坐标为(3×22018,×22018).
故答案为(3×22018,×22018).
三.解答题
21.解:(1)∵点P(m+3,2m﹣1)在y轴上,
∴m+3=0,
解得m=﹣3,
所以,2m﹣1=﹣2﹣1=﹣7,
所以,点P的坐标为(0,﹣7);
(2)∵点P的纵坐标比横坐标大3,
∴(2m﹣1)﹣(m+3)=3,
解得m=7,
∴7+3=7+3=10,2m﹣1=14﹣1=13,
所以,点P的坐标为(10,13);
(3)∵点P到x轴的距离为2,
∴|2m﹣1|=2,
解得m=或m=,
当m=时,m+3=,2m﹣1=3﹣1=2,
此时,点P(,2)(不合题意,舍去),
当m=时,m+3=,2m﹣1=﹣1﹣1=﹣2,
此时,点P(,﹣2),
∵点P在第四象限,
∴点P的坐标为(,﹣2).
22.解:选择出发点O为原点,西东方向为横轴,南北方向为纵轴建立坐标系.
如图中每个单位长度表示10米,此时A点的坐标为(5,3),B点坐标为(﹣2,﹣4).
过点A作y轴平行线,过点B作x轴平行线,则两平行线交于点C.
在Rt△ABC中,AB=≈9.898.
9.898×10=98.98(米).
答:时小明和小东相距大约98.98米.
23.解:如图所示:以A点为原点,
∵在平行四边形ABCD中,AB=3,BC=4,∠A=60°,
∴AD=BC=4,CD=AB=3,
C点纵坐标为:4×sin60°=2,
∴A点坐标为:(0,0),B点坐标为:(3,0),C点坐标为:(5,2),
D点坐标为:(2,2).
24.解:若关于x轴对称,则得到方程组,解得;
若关于y轴对称,则得到方程组,解得;
若关于原点对称,则得到方程组,解得.
25.解:根据题意得到|3m﹣1|=3|m﹣2|,两边平方,解得m=
因而P的坐标是(,﹣),则OP=.
26.解:如图所示,
由等边三角形,得
B点的横坐标为3,
BC==3,
即B点的坐标为(3,3).
由等边三角形OAB关于x轴对称的图形是等边三角形OA′B′,得
B′点的坐标为(3,﹣3).
27.解:(1)因为正方形ABCD的各顶点A,B,C,D到两坐标轴的距离都相等,且A,B,C,D分别在第二、第三、第四、第一象限,正方形的边长为8,所以A,B,C,D的坐标分别是A(﹣4,4),B(﹣4,﹣4),C(4,﹣4),D(4,4).
(2)平移的规律是:纵坐标不变,横坐标加4,所以平移后A点的坐标是(0,4).
图形与坐标》单元测试题
一.选择题
1.在平面直角坐标系中有M,N两点,若以N点为原点建立直角坐标系,则点M的坐标为(3,5),若以M点为原点建立直角坐标系,则点N的坐标是( )
A.(﹣3,5)
B.(3,﹣5)
C.(﹣3,﹣5)
D.(3,5)
2.点M(2,3),N(﹣2,4),则MN应为( )
A.17
B.1
C.
D.
3.已知点A(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,则a=( )
A.a=0
B.a=﹣9
C.a=﹣9或a=
D.a=
4.下列关于A,B两点的说法中,正确的个数是( )
①如果点A与点B关于y轴对称,则它们的纵坐标相同
②如果点A与点B的纵坐标相同,则它们关于y轴对称
③如果点A与点B的横坐标相同,则它们关于x轴对称
④如果点A与点B关于x轴对称,则它们的横坐标相同
A.1个
B.2个
C.3个
D.4个
5.如果把点A(﹣1,4)向右平移2个单位长度,再向上平移3个单位长度,则平移后的坐标是( )
A.(1,7)
B.(﹣1,7)
C.(1,﹣7)
D.(﹣1,﹣7)
6.如图,一个动点P在平面直角坐标系中按箭头所示方向做折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),…,按这样的运动规律,经过第2013次运动后,动点P的坐标是( )
A.(2012,1)
B.(2012,2)
C.(2013,1)
D.(2013,2)
7.如图所示,某班教室有9排5列座位.1号同学说:“小明在我的右后方.”2号同学说:“小明在我的左后方.”3号同学说:“小明在我的左前方.”4号同学说:“小明离1号同学和3号同学的距离一样远.”根据上面4位同学的描述,可知“5号”小明的位置在( )
A.4排3列
B.4排5列
C.5排4列
D.5排5列
8.如图,△ABC三个顶点的坐标分别为A(﹣2,5),B(﹣5,1),C(﹣2,1),将△ABC绕点C按顺时针方向旋转90°,得到△DEC,则点D的坐标为( )
A.(1,2)
B.(2,1)
C.(1,1)
D.(2,2)
9.如图,△AOB关于x轴对称图形△A′OB,若△AOB内任意一点P的坐标是(a,b),则△A′OB中的对应点Q的坐标是( )
A.(a,b)
B.(﹣a,b)
C.(﹣a,﹣b)
D.(a,﹣b)
10.已知点P关于x轴对称的点的坐标为(2,﹣1),那么点P关于原点对称的点的坐标是( )
A.(1,﹣2)
B.(2,1)
C.(﹣2,﹣1)
D.(﹣2,1)
二.填空题
11.若点A(a,b)在第三象限,则点C(﹣a,b﹣5)在第
象限.
12.点P(1,2)关于点Q(﹣1,1)的对称点的坐标为
.
13.已知点P(﹣2,3)和点Q(2,﹣3),则P,Q两个点的位置关系是
.
14.已知点P(a,5)与Q(2,b)是关于x轴对称,则a=
,b=
.
15.在坐标平面内,已知点M(1,2)和点N(1,﹣4),那么线段MN的长为
个单位长度,MN中点的坐标为
.
16.两点(3,﹣4)、(5,a)间的距离是2,则a的值为
.
17.点M(﹣3,5)关于直线x=1对称的点M′的坐标为
.
18.如图所示,在一个规格为4×8的球台上,有两只小球P和Q,设小球P的位置用(1,3)表示,小球Q的位置用(7,2)表示,若击打小球P经过球台的边AB上的点O反弹后,恰好击中小球Q,则点O的位置可以表示为
.
19.如图,点A(0,0),向右平移1个单位,再向上平移1个单位,得到点A1;点A1向上平移1个单位,冉向右平移2个单位,得到点A2;点A2向上平移2个单位,再向右平移4个单位,得到点A3;点A3向上平移4个单位,再向右平移8个单位,得到点A4;…按这个规律平移得到点A2019,则点A2019的横坐标为
.
20.如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1,△A2A3B2,△A3A4B3,…,△AnAn+1Bn均为等边三角形,点A1,A2,A3,…,An+1在x轴的正半轴上依次排列,点B1,B2,B3,…,Bn在直线OD上依次排列,那么B2020的坐标为
.
三.解答题
21.已知点P(m+3,2m﹣1),试分别根据下列条件求出点P的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P到x轴的距离为2,且在第四象限.
22.小明和小东在沙滩上玩游戏,他们都从某一点出发,小明先是沿正东方向行走50米,然后沿正北方向走30米到达点A处;小东则是先沿正西方向行走20米,然后沿正南行走40米到达点B出,请问此时小明和小东相距大约多少米?
23.在平行四边形ABCD中,AB=3,BC=4,∠A=60°,建立适当的平面直角坐标系,把平行四边形ABCD的各个顶点的坐标写出来.(要求写出一组坐标即可)
24.已知点M(4p,4q+p)和点N(5﹣3q,2p﹣2)关于x轴对称,求P和Q的值,若M,N关于y轴对称呢?关于原点对称呢?
25.当m为何值时,点P(3m﹣1,m﹣2)到y轴的距离是到x轴距离的3倍?求出此时点P到原点的距离.
26.在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),求点B′的横坐标.
27.已知正方形的边长为8,它在平面直角坐标系中的位置如图所示,被坐标轴分为四个同样的小正方形.
(1)直接写出点A,B,C,D四个点的坐标;
(2)若将正方形向右平移4个单位长度,写出平移后A点的坐标.
参考答案与试题解析
一.选择题
1.解:以N点为原点建立直角坐标系,则点M的坐标为(3,5),
则以M点为原点建立直角坐标系(两直角坐标系x轴,y轴方向一致),N点的坐标是(﹣3,﹣5).
故选:C.
2.解:MN==.故选C.
3.解:∵点A(5a﹣7,﹣6a﹣2)在第二、四象限的角平分线上,
∴5a﹣7=﹣(﹣6a﹣2),
解得a=﹣9.
故选:B.
4.解:正确的是:①如果点A与点B关于y轴对称,则它们的纵坐标相同;
④如果点A与点B关于x轴对称,则它们的横坐标相同;
故正确的有两个;
故选:B.
5.解:A(﹣1,4)向右平移2个单位长度得到:(﹣1+2,4),
即:(1,4),
再向上平移3个单位长度得到:(1,4+3),
即:(1,7),
故选:A.
6.解:∵第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),
第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),…,
∴按这样的运动规律,第几次横坐标即为几,纵坐标为:1,0,2,0,1,0,2,0…4个一循环,
∵=503…1,
∴经过第2013次运动后,动点P的坐标是:(2013,1).
故选:C.
7.解:根据1号同学,2号同学,3号同学的说法,可知小明在第4列,再根据4号同学说:“小明离1号同学和3号同学的距离一样远”可得小明在第5排第4列.
故选:C.
8.解:∵A(﹣2,5),B(﹣5,1),C(﹣2,1),
∴AC=4,AC∥y轴,
∵△ABC绕点C按顺时针方向旋转90°,得到△DEC,
∴∠DCE=∠ACB=90°,CD=AC=4,
∴B,C,D三点在一条直线上,
∴D(2,1),
故选:B.
9.解:∵△AOB与△A'OB关于x轴对称,
∴点P(a,b)关于x轴的对称点为(a,﹣b),
∴点P的对应点Q的坐标是(a,﹣b).
故选:D.
10.解:根据轴对称的性质,得P点的坐标是(2,1).
再根据中心对称的性质,得点P关于原点对称的点的坐标是(﹣2,﹣1).
故选:C.
二.填空题
11.解:∵点A(a,b)在第三象限,
∴a<0,b<0,
∴﹣a>0,b﹣5<0,
∴点C(﹣a,b﹣5)在第四象限.
故答案为:四.
12.解:设点P(1,2)关于点Q(﹣1,1)的对称点的坐标为(a,b),
则=﹣1,=1,
解得:a=﹣3,b=0,
∴点P(1,2)关于点Q(﹣1,1)的对称点的坐标为(﹣3,0),
故答案为:(﹣3,0).
13.解:∵P,Q两个点的横纵坐标都互为相反数,∴P,Q两个点关于原点对称,
故答案为关于原点对称.
14.解:∵点P(a,5)与Q(2,b)是关于x轴对称,
∴a=2,b=﹣5,
故答案为:2,﹣5.
15.解:∵点M(1,2)和点N(1,﹣4)横坐标相等,
∴MN∥y轴,MN=2﹣(﹣4)=6,
MN中点的坐标为(1,),即(1,﹣1).
故答案填:6、(1,﹣1).
16.解:根据题意得=2,
解得a=﹣4.
故答案为﹣4.
17.解:∵点M(﹣3,5)与点N关于直线x=1对称,
而1×2﹣(﹣3)=5,
∴点M(﹣3,5)关于直线x=1对称的点N的坐标是(5,5),
故答案为(5,5).
18.解:如图所示,
O点的坐标为(3,4),
故答案为(3,4).
19.解:点A1的横坐标为1=21﹣1,点A2的横坐为标3=22﹣1,点A3:的横坐标为7=23﹣1,点A4的横坐标为15=24﹣1,
按这个规律平移得到点An为2n﹣1,
∴点A2018的横坐标为22019﹣1,
故答案为:22019﹣1.
20.解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠B1OA2=30°,
∴∠B1OA2=∠A1B1O=30°,
∴OA2=2OA1=2,
同理可得,OAn=2n﹣1,
∵∠BnOAn+1=30°,∠BnAnAn+1=60°,
∴∠BnOAn+1=∠OBnAn=30°,
∴BnAn=OAn=2n﹣1,
即△AnBnAn+1的边长为2n﹣1,
则可求得其高为×2n﹣1=×2n﹣2,
∴点Bn的横坐标为×2n﹣1+2n﹣1=×2n﹣1=3×2n﹣2,
∴点Bn的坐标为(3×2n﹣2,×2n﹣2),
∴点B2020的坐标为(3×22018,×22018).
故答案为(3×22018,×22018).
三.解答题
21.解:(1)∵点P(m+3,2m﹣1)在y轴上,
∴m+3=0,
解得m=﹣3,
所以,2m﹣1=﹣2﹣1=﹣7,
所以,点P的坐标为(0,﹣7);
(2)∵点P的纵坐标比横坐标大3,
∴(2m﹣1)﹣(m+3)=3,
解得m=7,
∴7+3=7+3=10,2m﹣1=14﹣1=13,
所以,点P的坐标为(10,13);
(3)∵点P到x轴的距离为2,
∴|2m﹣1|=2,
解得m=或m=,
当m=时,m+3=,2m﹣1=3﹣1=2,
此时,点P(,2)(不合题意,舍去),
当m=时,m+3=,2m﹣1=﹣1﹣1=﹣2,
此时,点P(,﹣2),
∵点P在第四象限,
∴点P的坐标为(,﹣2).
22.解:选择出发点O为原点,西东方向为横轴,南北方向为纵轴建立坐标系.
如图中每个单位长度表示10米,此时A点的坐标为(5,3),B点坐标为(﹣2,﹣4).
过点A作y轴平行线,过点B作x轴平行线,则两平行线交于点C.
在Rt△ABC中,AB=≈9.898.
9.898×10=98.98(米).
答:时小明和小东相距大约98.98米.
23.解:如图所示:以A点为原点,
∵在平行四边形ABCD中,AB=3,BC=4,∠A=60°,
∴AD=BC=4,CD=AB=3,
C点纵坐标为:4×sin60°=2,
∴A点坐标为:(0,0),B点坐标为:(3,0),C点坐标为:(5,2),
D点坐标为:(2,2).
24.解:若关于x轴对称,则得到方程组,解得;
若关于y轴对称,则得到方程组,解得;
若关于原点对称,则得到方程组,解得.
25.解:根据题意得到|3m﹣1|=3|m﹣2|,两边平方,解得m=
因而P的坐标是(,﹣),则OP=.
26.解:如图所示,
由等边三角形,得
B点的横坐标为3,
BC==3,
即B点的坐标为(3,3).
由等边三角形OAB关于x轴对称的图形是等边三角形OA′B′,得
B′点的坐标为(3,﹣3).
27.解:(1)因为正方形ABCD的各顶点A,B,C,D到两坐标轴的距离都相等,且A,B,C,D分别在第二、第三、第四、第一象限,正方形的边长为8,所以A,B,C,D的坐标分别是A(﹣4,4),B(﹣4,﹣4),C(4,﹣4),D(4,4).
(2)平移的规律是:纵坐标不变,横坐标加4,所以平移后A点的坐标是(0,4).
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
