三年级下册数学教案-7.4 周长与面积 沪教版
文档属性
| 名称 | 三年级下册数学教案-7.4 周长与面积 沪教版 |  | |
| 格式 | doc | ||
| 文件大小 | 301.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 07:21:17 | ||
图片预览

文档简介
周长与面积
【教学内容】沪教版三年级数学第二学期第五单元:周长与面积
【教学目标】
在动手操作与合作交流的过程中,探索根据长方形(正方形)周长求其的面积,以及根据长方形的面积求其周长的基本策略。
经历从生活情境中提炼数学信息的过程,并运用长方形(正方形)周长和面积的关系,分析、解决实际问题。
3、通过对长方形(正方形)面积与周长的相关问题的讨论、探究,经历运用操作帮助思考的学习过程,体验自主解决数学问题的快乐与自信。
【教学重点】根据长方形、正方形的周长(面积),求出其面积(周长)。
【教学难点】根据长方形(面积),分析其周长的多种可能。
【教具准备】28厘米长的扭扭棒、学习单、媒体。
【教学过程】
一、创设情境,导入新课
活动一:这里有两张破损的长方形纸片,如果要知道它们原来的周长和面积,我们该怎么办呢?
学生预测反馈:测量它们的长和宽。
师:请你量一量,把数据记录下来,并计算一下。(板贴:周长、面积)
投影仪展示计算过程。
1、师:他算出的周长是12厘米,面积是9平方厘米。你们同意吗?
在测量的时候你发现了什么?
学生预设:我发现了这个长方形长和宽相等,是一个正方形。(板贴:正方形)
师:所以我们可以用什么方法来求出正方形的周长和面积?
学生预设:正方形周长=4х边长;正方形面积=边长х边长。(板贴)
2、师:长方形的周长是16厘米,面积12平方厘米。你们同意吗?怎么计算长方形周长和面积?
学生预测回答:长方形周长=2х(长+宽);正方形面积=长х宽。(板贴)
【通过活动,学生能进一步感受求长方形(正方形)的面积和周长的必要条件是长和宽(边长)。回顾复习长方形、正方形的周长和面积的计算方法。】
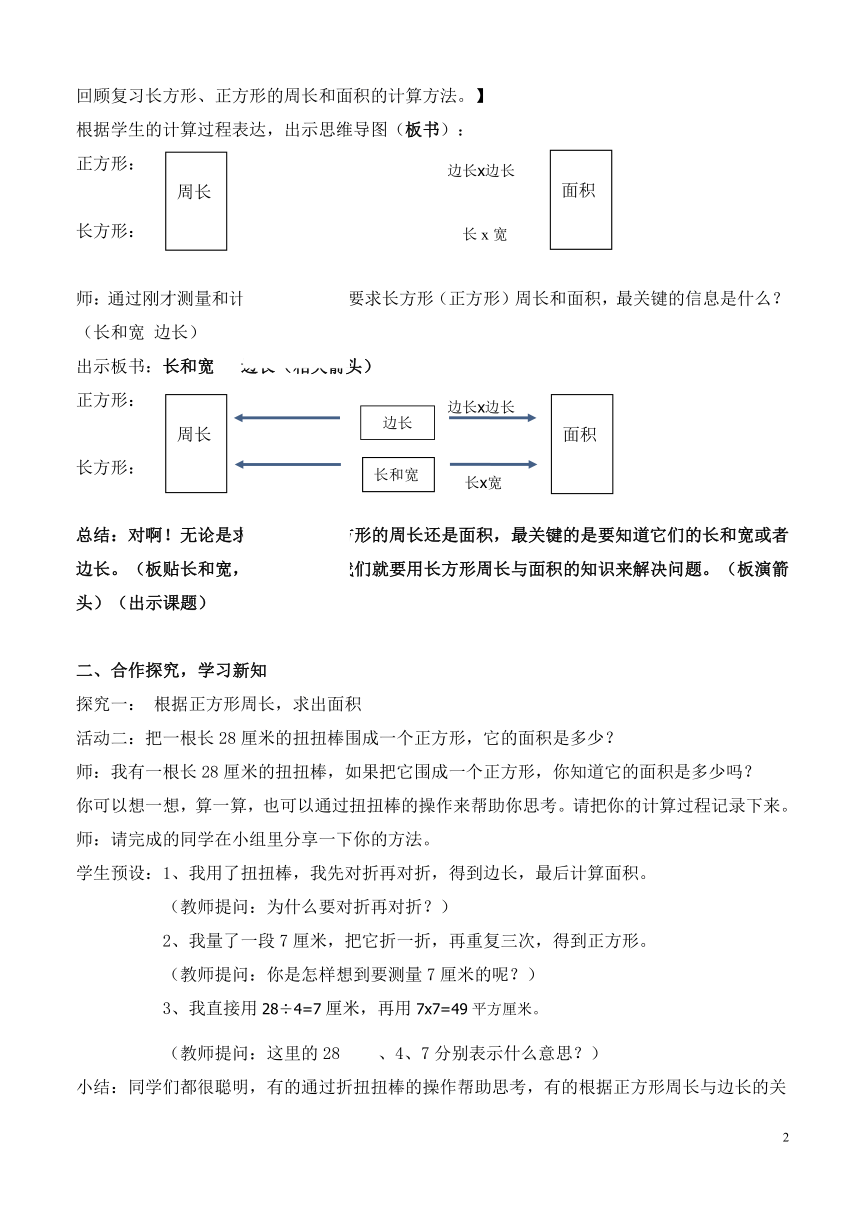
根据学生的计算过程表达,出示思维导图(板书):
正方形:
长方形:
师:通过刚才测量和计算,你们认为要求长方形(正方形)周长和面积,最关键的信息是什么?(长和宽 边长)
出示板书:长和宽 边长(相关箭头)
正方形:
长方形:
总结:对啊!无论是求长方形和正方形的周长还是面积,最关键的是要知道它们的长和宽或者边长。(板贴长和宽,边长)今天我们就要用长方形周长与面积的知识来解决问题。(板演箭头)(出示课题)
二、合作探究,学习新知
探究一: 根据正方形周长,求出面积
活动二:把一根长28厘米的扭扭棒围成一个正方形,它的面积是多少?
师:我有一根长28厘米的扭扭棒,如果把它围成一个正方形,你知道它的面积是多少吗?
你可以想一想,算一算,也可以通过扭扭棒的操作来帮助你思考。请把你的计算过程记录下来。
师:请完成的同学在小组里分享一下你的方法。
学生预设:1、我用了扭扭棒,我先对折再对折,得到边长,最后计算面积。
(教师提问:为什么要对折再对折?)
2、我量了一段7厘米,把它折一折,再重复三次,得到正方形。
(教师提问:你是怎样想到要测量7厘米的呢?)
3、我直接用28÷4=7厘米,再用7х7=49平方厘米。
(教师提问:这里的28 、4、7分别表示什么意思?)
小结:同学们都很聪明,有的通过折扭扭棒的操作帮助思考,有的根据正方形周长与边长的关系直接计算都解决了这个问题。
师:但是不管通过什么方法,我们都要先求什么?(边长)怎么求?(板贴周长除以4)
总结:通过同学们独立探究、合作讨论,我们在根据边长求正方形面积的基础上,自己发现通过正方形的周长求它出面积的方法(板演:箭头),真了不起!
【以操作为辅助,学生能在教学活动中经历根据正方形周长求面积的整个过程,提高自己比较概括,分析提炼的能力,并初步掌握正方形周长和面积的转换方法。】
正方形:
探究二:根据长方形周长,求面积
活动三:用一根长28cm的扭扭棒,围成一个宽为3cm长方形,它的面积是多少?
师:现在如果要把这根扭扭棒围一个长方形,它的面积又是多少呢?请你解决今天的第二个问题。
学生预设:28-3=25 25х3=75; 28-3х2=22 22х3=66;
(28-3х2)÷2=11 11х3=33; 28÷2-3=11 11х3=33;
师:1、你能读懂吗?小组里交流一下吧。
2、这些算式你是直接计算的还是用了扭扭棒?你是怎么用扭扭棒的?介绍一下你的方法。
学生预设:把扭扭棒对折,先量宽,剩下的就是长。
师预设:那对折求的是什么?(长与宽的和)你们同意他的折法吗?
师:这位同学准确地得到了长方形的长,但有个小小的缺陷,它围不成一个长方形,那怎么办?
学生预设:1、剪下来再围。2、对折后,一边从头量3cm,一边从中间量3cm,再折一折。
小结:那在已知长方形周长要求面积的问题中,什么是关键?(长和宽)你是怎么求的?(周长÷2-长(宽)或(周长-2х宽)÷2)板贴:周长÷2-长(宽),板演:箭头
长方形:
总结:刚才我们借助了扭扭棒解决了已知长方形周长求面积的问题。接下来有个更难的问题等着我们挑战,你们有没有信心?
探究三:根据长方形面积,求周长
活动四:在16平方厘米的玻璃周围绑一圈胶带,需要准备多长的胶带?(接缝处不算)
师:小丁丁真是一个助人为乐的好孩子,在下面这个情景中,我们可以找到哪些数学信息?已知什么?求什么?请你们小组讨论一下,如何解决这个问题。
【学生经历问题解决的过程,在这基础上初步体会长方形与正方形周长和面积的关系。通过交流讨论,在实际情境中,提高分析、概括和解决问题的能力。】
学生预设:这是已知面积,求周长的问题。我们觉得要找长和宽相乘是16。宽是1cm,长就是16cm;宽是2cm,长就是8sm;宽是4cm,长就是4cm,就是正方形。
师预设:其实就是设定它的长,然后用面积除以长得到了宽。(板书:周长÷长(宽))
(4x4的情况)这是一个什么图形?面积是哪些数据时,可能产生正方形?(平方数)
教师小结:当面积是一个表内平方数的时候,我们可以想到两个相同的因数,就是这个正方形的边长,最后求得它的周长。(板书:(边长)х(边长))
正方形:
长方形:
总结:通过思考和交流,我们发现了在已知长方形或正方形的面积的情况下,也可以求出它的周长。
三、总结交流,提升自我
通过今天的数学活动,你有什么感受?
(预设:求长方形的面积和周长,长和宽是关键条件,求正方形的面积和周长,边长是关键条件;在遇到比较难得问题是,可以通过操作帮助我们思考)
板书设计 周长与面积
正方形:
长方形:
1
【教学内容】沪教版三年级数学第二学期第五单元:周长与面积
【教学目标】
在动手操作与合作交流的过程中,探索根据长方形(正方形)周长求其的面积,以及根据长方形的面积求其周长的基本策略。
经历从生活情境中提炼数学信息的过程,并运用长方形(正方形)周长和面积的关系,分析、解决实际问题。
3、通过对长方形(正方形)面积与周长的相关问题的讨论、探究,经历运用操作帮助思考的学习过程,体验自主解决数学问题的快乐与自信。
【教学重点】根据长方形、正方形的周长(面积),求出其面积(周长)。
【教学难点】根据长方形(面积),分析其周长的多种可能。
【教具准备】28厘米长的扭扭棒、学习单、媒体。
【教学过程】
一、创设情境,导入新课
活动一:这里有两张破损的长方形纸片,如果要知道它们原来的周长和面积,我们该怎么办呢?
学生预测反馈:测量它们的长和宽。
师:请你量一量,把数据记录下来,并计算一下。(板贴:周长、面积)
投影仪展示计算过程。
1、师:他算出的周长是12厘米,面积是9平方厘米。你们同意吗?
在测量的时候你发现了什么?
学生预设:我发现了这个长方形长和宽相等,是一个正方形。(板贴:正方形)
师:所以我们可以用什么方法来求出正方形的周长和面积?
学生预设:正方形周长=4х边长;正方形面积=边长х边长。(板贴)
2、师:长方形的周长是16厘米,面积12平方厘米。你们同意吗?怎么计算长方形周长和面积?
学生预测回答:长方形周长=2х(长+宽);正方形面积=长х宽。(板贴)
【通过活动,学生能进一步感受求长方形(正方形)的面积和周长的必要条件是长和宽(边长)。回顾复习长方形、正方形的周长和面积的计算方法。】
根据学生的计算过程表达,出示思维导图(板书):
正方形:
长方形:
师:通过刚才测量和计算,你们认为要求长方形(正方形)周长和面积,最关键的信息是什么?(长和宽 边长)
出示板书:长和宽 边长(相关箭头)
正方形:
长方形:
总结:对啊!无论是求长方形和正方形的周长还是面积,最关键的是要知道它们的长和宽或者边长。(板贴长和宽,边长)今天我们就要用长方形周长与面积的知识来解决问题。(板演箭头)(出示课题)
二、合作探究,学习新知
探究一: 根据正方形周长,求出面积
活动二:把一根长28厘米的扭扭棒围成一个正方形,它的面积是多少?
师:我有一根长28厘米的扭扭棒,如果把它围成一个正方形,你知道它的面积是多少吗?
你可以想一想,算一算,也可以通过扭扭棒的操作来帮助你思考。请把你的计算过程记录下来。
师:请完成的同学在小组里分享一下你的方法。
学生预设:1、我用了扭扭棒,我先对折再对折,得到边长,最后计算面积。
(教师提问:为什么要对折再对折?)
2、我量了一段7厘米,把它折一折,再重复三次,得到正方形。
(教师提问:你是怎样想到要测量7厘米的呢?)
3、我直接用28÷4=7厘米,再用7х7=49平方厘米。
(教师提问:这里的28 、4、7分别表示什么意思?)
小结:同学们都很聪明,有的通过折扭扭棒的操作帮助思考,有的根据正方形周长与边长的关系直接计算都解决了这个问题。
师:但是不管通过什么方法,我们都要先求什么?(边长)怎么求?(板贴周长除以4)
总结:通过同学们独立探究、合作讨论,我们在根据边长求正方形面积的基础上,自己发现通过正方形的周长求它出面积的方法(板演:箭头),真了不起!
【以操作为辅助,学生能在教学活动中经历根据正方形周长求面积的整个过程,提高自己比较概括,分析提炼的能力,并初步掌握正方形周长和面积的转换方法。】
正方形:
探究二:根据长方形周长,求面积
活动三:用一根长28cm的扭扭棒,围成一个宽为3cm长方形,它的面积是多少?
师:现在如果要把这根扭扭棒围一个长方形,它的面积又是多少呢?请你解决今天的第二个问题。
学生预设:28-3=25 25х3=75; 28-3х2=22 22х3=66;
(28-3х2)÷2=11 11х3=33; 28÷2-3=11 11х3=33;
师:1、你能读懂吗?小组里交流一下吧。
2、这些算式你是直接计算的还是用了扭扭棒?你是怎么用扭扭棒的?介绍一下你的方法。
学生预设:把扭扭棒对折,先量宽,剩下的就是长。
师预设:那对折求的是什么?(长与宽的和)你们同意他的折法吗?
师:这位同学准确地得到了长方形的长,但有个小小的缺陷,它围不成一个长方形,那怎么办?
学生预设:1、剪下来再围。2、对折后,一边从头量3cm,一边从中间量3cm,再折一折。
小结:那在已知长方形周长要求面积的问题中,什么是关键?(长和宽)你是怎么求的?(周长÷2-长(宽)或(周长-2х宽)÷2)板贴:周长÷2-长(宽),板演:箭头
长方形:
总结:刚才我们借助了扭扭棒解决了已知长方形周长求面积的问题。接下来有个更难的问题等着我们挑战,你们有没有信心?
探究三:根据长方形面积,求周长
活动四:在16平方厘米的玻璃周围绑一圈胶带,需要准备多长的胶带?(接缝处不算)
师:小丁丁真是一个助人为乐的好孩子,在下面这个情景中,我们可以找到哪些数学信息?已知什么?求什么?请你们小组讨论一下,如何解决这个问题。
【学生经历问题解决的过程,在这基础上初步体会长方形与正方形周长和面积的关系。通过交流讨论,在实际情境中,提高分析、概括和解决问题的能力。】
学生预设:这是已知面积,求周长的问题。我们觉得要找长和宽相乘是16。宽是1cm,长就是16cm;宽是2cm,长就是8sm;宽是4cm,长就是4cm,就是正方形。
师预设:其实就是设定它的长,然后用面积除以长得到了宽。(板书:周长÷长(宽))
(4x4的情况)这是一个什么图形?面积是哪些数据时,可能产生正方形?(平方数)
教师小结:当面积是一个表内平方数的时候,我们可以想到两个相同的因数,就是这个正方形的边长,最后求得它的周长。(板书:(边长)х(边长))
正方形:
长方形:
总结:通过思考和交流,我们发现了在已知长方形或正方形的面积的情况下,也可以求出它的周长。
三、总结交流,提升自我
通过今天的数学活动,你有什么感受?
(预设:求长方形的面积和周长,长和宽是关键条件,求正方形的面积和周长,边长是关键条件;在遇到比较难得问题是,可以通过操作帮助我们思考)
板书设计 周长与面积
正方形:
长方形:
1
