2020-2021学年苏科版八年级数学下册第四周周末强化提优试卷(10.3-10.4)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册第四周周末强化提优试卷(10.3-10.4)(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 967.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-25 00:00:00 | ||
图片预览

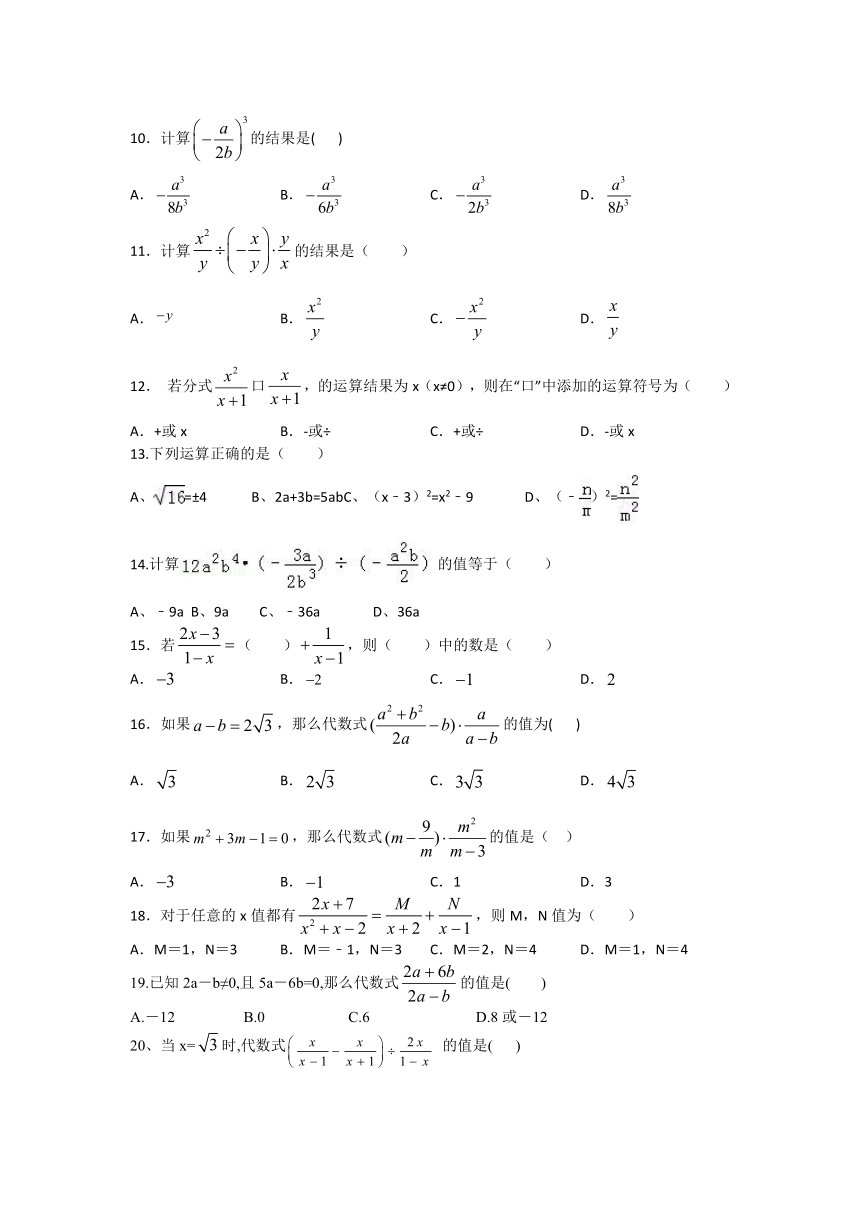
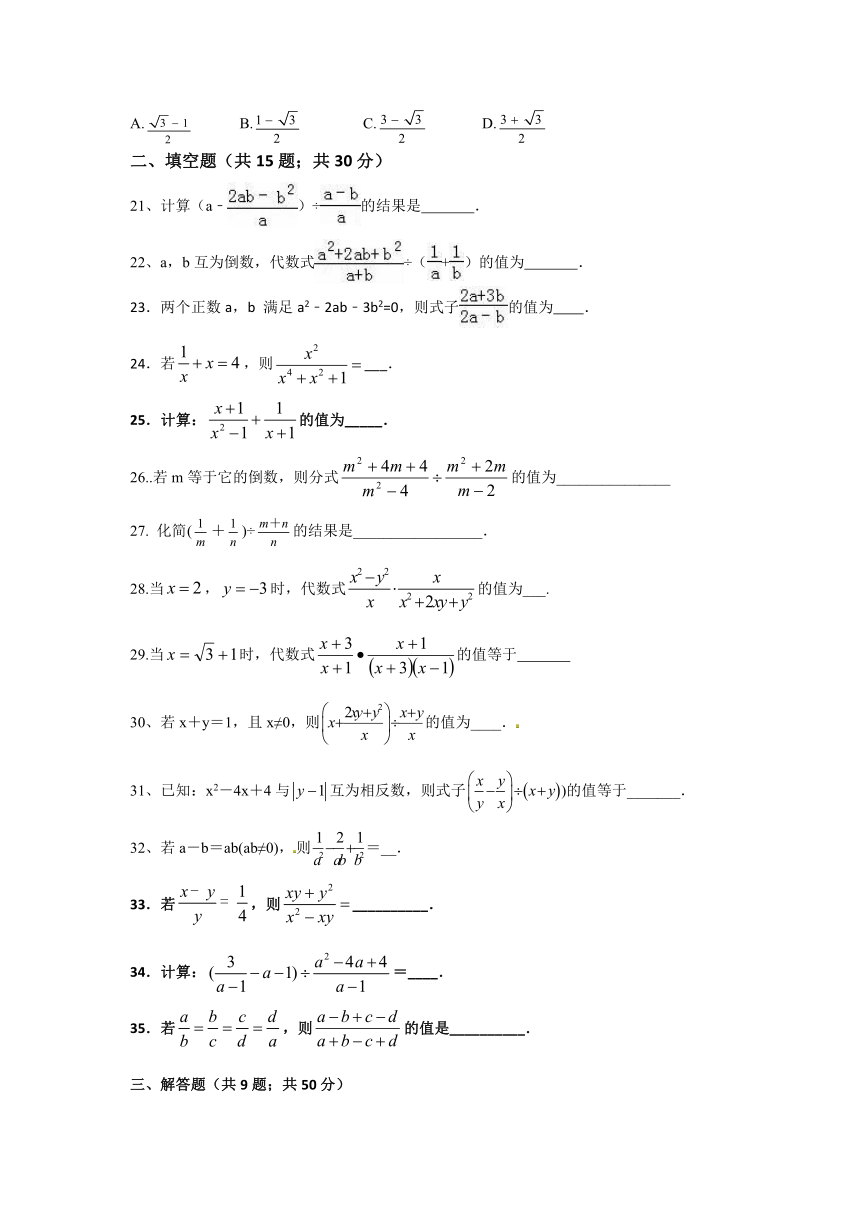


文档简介
苏科版八年级数学下册第四周周末强化提优试卷(10.3-10.4)
(时间:90分钟 满分:120分)
选择题(共20题;共40分)
1.若分式的值为0,则b的值为( )
A.1 B.-1 C.±1 D.2
2.完分式运算后,老师出了一道题“化简+”,小明的做法是:原式=-==;小亮的做法是:原式=(x+3)(x-2)+(2-x)=x2+x-6+2-x=x2-4;小芳的做法是:原式=-=-==1,其中正确的是( )
A.小明 B.小亮 C.小芳 D.没有正确的
3. 已知,则的值为( C )
A. B. C. D. 2
4.若方程,则A、B的值分别为( )
A. B. C. D.
5.已知,则的值为( B )
A. B. C. 2 D.
6.设,若n的值为整数,则x可以取的值的个数是( )
A. 5 B. 4 C. 3 D. 2
7.已知x2﹣3x﹣4=0,则代数式的值是( )
A.3 B.2 C. D.
8.若把分式中的x和y都扩大到原来的10倍,则分式的值( )
A.扩大到原来的10倍 B.不变C.缩小到原来的 D.缩小到原来的
9.,,都有意义,下列等式①;②;③;④中一定不成立的是( )
A.②④ B.①④ C.①②③④ D.②
10.计算的结果是( )
A. B. C. D.
11.计算的结果是( )
A. B. C. D.
12. 若分式口,的运算结果为x(x≠0),则在“口”中添加的运算符号为( )
A.+或x B.-或÷ C.+或÷ D.-或x
13.下列运算正确的是( )
A、=±4 B、2a+3b=5abC、(x﹣3)2=x2﹣9 D、(﹣)2=
14.计算的值等于( )
A、﹣9a B、9a C、﹣36a D、36a
15.若( ),则( )中的数是( )
A. B. C. D.
16.如果,那么代数式的值为( )
A. B. C. D.
17.如果,那么代数式的值是( )
A. B. C.1 D.3
18.对于任意的x值都有,则M,N值为( )
A.M=1,N=3 B.M=﹣1,N=3 C.M=2,N=4 D.M=1,N=4
19.已知2a-b≠0,且5a-6b=0,那么代数式的值是( )
A.-12 B.0 C.6 D.8或-12
20、当x=时,代数式 的值是( )
A. B. C. D.
填空题(共15题;共30分)
21、计算(a﹣)÷的结果是 .
22、a,b互为倒数,代数式÷(+)的值为 .
23.两个正数a,b 满足a2﹣2ab﹣3b2=0,则式子的值为 .
24.若,则___.
25.计算:的值为_____.
26..若m等于它的倒数,则分式的值为_______________
化简(+)÷的结果是_________________.
28.当,时,代数式的值为___.
29.当时,代数式的值等于
若x+y=1,且x≠0,则的值为____.
已知:x2-4x+4与互为相反数,则式子)的值等于_______.
若a-b=ab(ab≠0),则=__.
33.若,则__________.
34.计算:=____.
35.若,则的值是__________.
解答题(共9题;共50分)
36计算:.
37.计算:.
38.先化简,再求值:(),其中a=2.
先化简,再求值:,在1,2,3三个数中选一个恰当的数,代入求值.
已知,试求的值.
探索:
(1)如果=3+,则m= ;
(2)如果=5+,则m= ;
总结:如果=a+(其中a、b、c为常数),则m= ;
应用:利用上述结论解决:若代数式的值为整数,求满足条件的整数x的值.
已知a,b,c均为非零实数,且满足==,求:的值.
43.观察下列各组式子:
①;②;③
(1)请根据上面的规律写出第 个式子;
(2)请写出第个式子,并证明你发现的规律.
44.不等于0的三个数、、满足,求证:、、中至少有两个互为相反数.
教师样卷
选择题(共20题;共40分)
1.若分式的值为0,则b的值为( A )
A.1 B.-1 C.±1 D.2
2.完分式运算后,老师出了一道题“化简+”,小明的做法是:原式=-==;小亮的做法是:原式=(x+3)(x-2)+(2-x)=x2+x-6+2-x=x2-4;小芳的做法是:原式=-=-==1,其中正确的是( C )
A.小明 B.小亮 C.小芳 D.没有正确的
3. 已知,则的值为( C )
A. B. C. D. 2
4.若方程,则A、B的值分别为( C )
A. B. C. D.
5.已知,则的值为( B )
A. B. C. 2 D.
6.设,若n的值为整数,则x可以取的值的个数是( B )
A. 5 B. 4 C. 3 D. 2
7.已知x2﹣3x﹣4=0,则代数式的值是( D )
A.3 B.2 C. D.
8.若把分式中的x和y都扩大到原来的10倍,则分式的值( C )
A.扩大到原来的10倍 B.不变C.缩小到原来的 D.缩小到原来的
9.,,都有意义,下列等式①;②;③;④中一定不成立的是( D )
A.②④ B.①④ C.①②③④ D.②
解:∵ ,,都有意义,∴ ,,,①,仅需,即时成立;②,不成立;
③,(右侧分子分母同时除以2),因此成立;④,即,当时成立;故仅有②一定不成立,故选D
10.计算的结果是( A )
A. B. C. D.
解: .故选:A.
11.计算的结果是( A )
A. B. C. D.
解:原式= 故选:A.
12. 若分式口,的运算结果为x(x≠0),则在“口”中添加的运算符号为( C )
A.+或x B.-或÷ C.+或÷ D.-或x
【详解】
综上,在“口”中添加的运算符号为或故选:C.
13.下列运算正确的是( B )
A、=±4 B、2a+3b=5abC、(x﹣3)2=x2﹣9 D、(﹣)2=
14.计算的值等于( D )
A、﹣9a B、9a C、﹣36a D、36a
15.若( ),则( )中的数是( B )
A. B. C. D.
【详解】
故选:B.
16.如果,那么代数式的值为( A )
A. B. C. D.
详解:原式,∵,∴原式.
故选A.
17.如果,那么代数式的值是( C )
A. B. C.1 D.3
解:原式====,
∵,∴,则原式=1,故选C.
18.对于任意的x值都有,则M,N值为( B )
A.M=1,N=3 B.M=﹣1,N=3 C.M=2,N=4 D.M=1,N=4
解:==
∴=∴,解得:,故选:B.
19.已知2a-b≠0,且5a-6b=0,那么代数式的值是( C )
A.-12 B.0 C.6 D.8或-12
20、当x=时,代数式 的值是( B )
A. B. C. D.
二. 填空题(共15题;共30分)
21、计算(a﹣)÷的结果是 a-b .
22、a,b互为倒数,代数式÷(+)的值为 1 .
23.两个正数a,b 满足a2﹣2ab﹣3b2=0,则式子的值为 .
【解答】解:∵a2﹣2ab﹣3b2=0,∴(a﹣3b)(a+b)=0,∵两个正数a,b,∴a﹣3b=0,
∴a=3b,∴==.故答案为:.
24.若,则___.
解:平方后得:,所以.
故答案为:.
25.计算:的值为_____.
【答案】 解:==
==故答案为:.
26..若m等于它的倒数,则分式的值为_______________
【答案】±1
化简(+)÷的结果是_________________.
【答案】
28.当,时,代数式的值为___.
【答案】-5
29.当时,代数式的值等于
【答案】
若x+y=1,且x≠0,则的值为____.
【答案】1
已知:x2-4x+4与互为相反数,则式子)的值等于_______.
【答案】
若a-b=ab(ab≠0),则=__.
【答案】1
33.若,则__________.
【答案】 解:∵∴∴∴∴原式.故答案是:
34.计算:=____.
【答案】.【详解】原式= =
=.故答案为:.
35.若,则的值是__________.
【答案】0或-2 【详解】设,则,,,.故,.若,则;
若,则.
解答题(共9题;共50分)
36计算:.
解:原式.?
37.计算:.
解:原式,,.??
38.先化简,再求值:(),其中a=2.
【答案】,4
【详解】()
,当a=2时,原式.
39.先化简,再求值:,在1,2,3三个数中选一个恰当的数,代入求值.
【答案】,.
【详解】原式
根据分式有意义的条件得,且则将代入得,原式.
已知,试求的值.
解:
探索:
(1)如果=3+,则m= 1 ;
(2)如果=5+,则m= ﹣13 ;
总结:如果=a+(其中a、b、c为常数),则m b﹣ac ;
应用:利用上述结论解决:若代数式的值为整数,求满足条件的整数x的值.
解:探索:(1)已知等式整理得: =,即3x+4=3x+3+m,
解得:m=1;故答案为:1;﹣13
(2)已知等式整理得: =,即5x﹣3=5x+10+m,
解得:m=﹣13;总结:m=b﹣ac; 故答案为:m=b﹣ac;
应用: ==4+,∵x为整数且为整数,∴x﹣1=±1,
∴x=2或0.
42.已知a,b,c均为非零实数,且满足==,求:的值.
解:∵==,∴=1,
∴===1,∴a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
即a+b=2c,a+c=2b,b+c=2a,∴==8.
43.观察下列各组式子:
①;②;③
(1)请根据上面的规律写出第 个式子;
(2)请写出第个式子,并证明你发现的规律.
【答案】(1);(2),证明
【详解】(1)(2)
证明:等式左边,
∵等式右边为,与等式左边计算出的结果相等,
∴成立.
44.不等于0的三个数、、满足,求证:、、中至少有两个互为相反数.
【详解】①若,则∴.∴.∴.∴.∴或.
②若,则、互为相反数综上所述、、中必有两个互为相反数.
(时间:90分钟 满分:120分)
选择题(共20题;共40分)
1.若分式的值为0,则b的值为( )
A.1 B.-1 C.±1 D.2
2.完分式运算后,老师出了一道题“化简+”,小明的做法是:原式=-==;小亮的做法是:原式=(x+3)(x-2)+(2-x)=x2+x-6+2-x=x2-4;小芳的做法是:原式=-=-==1,其中正确的是( )
A.小明 B.小亮 C.小芳 D.没有正确的
3. 已知,则的值为( C )
A. B. C. D. 2
4.若方程,则A、B的值分别为( )
A. B. C. D.
5.已知,则的值为( B )
A. B. C. 2 D.
6.设,若n的值为整数,则x可以取的值的个数是( )
A. 5 B. 4 C. 3 D. 2
7.已知x2﹣3x﹣4=0,则代数式的值是( )
A.3 B.2 C. D.
8.若把分式中的x和y都扩大到原来的10倍,则分式的值( )
A.扩大到原来的10倍 B.不变C.缩小到原来的 D.缩小到原来的
9.,,都有意义,下列等式①;②;③;④中一定不成立的是( )
A.②④ B.①④ C.①②③④ D.②
10.计算的结果是( )
A. B. C. D.
11.计算的结果是( )
A. B. C. D.
12. 若分式口,的运算结果为x(x≠0),则在“口”中添加的运算符号为( )
A.+或x B.-或÷ C.+或÷ D.-或x
13.下列运算正确的是( )
A、=±4 B、2a+3b=5abC、(x﹣3)2=x2﹣9 D、(﹣)2=
14.计算的值等于( )
A、﹣9a B、9a C、﹣36a D、36a
15.若( ),则( )中的数是( )
A. B. C. D.
16.如果,那么代数式的值为( )
A. B. C. D.
17.如果,那么代数式的值是( )
A. B. C.1 D.3
18.对于任意的x值都有,则M,N值为( )
A.M=1,N=3 B.M=﹣1,N=3 C.M=2,N=4 D.M=1,N=4
19.已知2a-b≠0,且5a-6b=0,那么代数式的值是( )
A.-12 B.0 C.6 D.8或-12
20、当x=时,代数式 的值是( )
A. B. C. D.
填空题(共15题;共30分)
21、计算(a﹣)÷的结果是 .
22、a,b互为倒数,代数式÷(+)的值为 .
23.两个正数a,b 满足a2﹣2ab﹣3b2=0,则式子的值为 .
24.若,则___.
25.计算:的值为_____.
26..若m等于它的倒数,则分式的值为_______________
化简(+)÷的结果是_________________.
28.当,时,代数式的值为___.
29.当时,代数式的值等于
若x+y=1,且x≠0,则的值为____.
已知:x2-4x+4与互为相反数,则式子)的值等于_______.
若a-b=ab(ab≠0),则=__.
33.若,则__________.
34.计算:=____.
35.若,则的值是__________.
解答题(共9题;共50分)
36计算:.
37.计算:.
38.先化简,再求值:(),其中a=2.
先化简,再求值:,在1,2,3三个数中选一个恰当的数,代入求值.
已知,试求的值.
探索:
(1)如果=3+,则m= ;
(2)如果=5+,则m= ;
总结:如果=a+(其中a、b、c为常数),则m= ;
应用:利用上述结论解决:若代数式的值为整数,求满足条件的整数x的值.
已知a,b,c均为非零实数,且满足==,求:的值.
43.观察下列各组式子:
①;②;③
(1)请根据上面的规律写出第 个式子;
(2)请写出第个式子,并证明你发现的规律.
44.不等于0的三个数、、满足,求证:、、中至少有两个互为相反数.
教师样卷
选择题(共20题;共40分)
1.若分式的值为0,则b的值为( A )
A.1 B.-1 C.±1 D.2
2.完分式运算后,老师出了一道题“化简+”,小明的做法是:原式=-==;小亮的做法是:原式=(x+3)(x-2)+(2-x)=x2+x-6+2-x=x2-4;小芳的做法是:原式=-=-==1,其中正确的是( C )
A.小明 B.小亮 C.小芳 D.没有正确的
3. 已知,则的值为( C )
A. B. C. D. 2
4.若方程,则A、B的值分别为( C )
A. B. C. D.
5.已知,则的值为( B )
A. B. C. 2 D.
6.设,若n的值为整数,则x可以取的值的个数是( B )
A. 5 B. 4 C. 3 D. 2
7.已知x2﹣3x﹣4=0,则代数式的值是( D )
A.3 B.2 C. D.
8.若把分式中的x和y都扩大到原来的10倍,则分式的值( C )
A.扩大到原来的10倍 B.不变C.缩小到原来的 D.缩小到原来的
9.,,都有意义,下列等式①;②;③;④中一定不成立的是( D )
A.②④ B.①④ C.①②③④ D.②
解:∵ ,,都有意义,∴ ,,,①,仅需,即时成立;②,不成立;
③,(右侧分子分母同时除以2),因此成立;④,即,当时成立;故仅有②一定不成立,故选D
10.计算的结果是( A )
A. B. C. D.
解: .故选:A.
11.计算的结果是( A )
A. B. C. D.
解:原式= 故选:A.
12. 若分式口,的运算结果为x(x≠0),则在“口”中添加的运算符号为( C )
A.+或x B.-或÷ C.+或÷ D.-或x
【详解】
综上,在“口”中添加的运算符号为或故选:C.
13.下列运算正确的是( B )
A、=±4 B、2a+3b=5abC、(x﹣3)2=x2﹣9 D、(﹣)2=
14.计算的值等于( D )
A、﹣9a B、9a C、﹣36a D、36a
15.若( ),则( )中的数是( B )
A. B. C. D.
【详解】
故选:B.
16.如果,那么代数式的值为( A )
A. B. C. D.
详解:原式,∵,∴原式.
故选A.
17.如果,那么代数式的值是( C )
A. B. C.1 D.3
解:原式====,
∵,∴,则原式=1,故选C.
18.对于任意的x值都有,则M,N值为( B )
A.M=1,N=3 B.M=﹣1,N=3 C.M=2,N=4 D.M=1,N=4
解:==
∴=∴,解得:,故选:B.
19.已知2a-b≠0,且5a-6b=0,那么代数式的值是( C )
A.-12 B.0 C.6 D.8或-12
20、当x=时,代数式 的值是( B )
A. B. C. D.
二. 填空题(共15题;共30分)
21、计算(a﹣)÷的结果是 a-b .
22、a,b互为倒数,代数式÷(+)的值为 1 .
23.两个正数a,b 满足a2﹣2ab﹣3b2=0,则式子的值为 .
【解答】解:∵a2﹣2ab﹣3b2=0,∴(a﹣3b)(a+b)=0,∵两个正数a,b,∴a﹣3b=0,
∴a=3b,∴==.故答案为:.
24.若,则___.
解:平方后得:,所以.
故答案为:.
25.计算:的值为_____.
【答案】 解:==
==故答案为:.
26..若m等于它的倒数,则分式的值为_______________
【答案】±1
化简(+)÷的结果是_________________.
【答案】
28.当,时,代数式的值为___.
【答案】-5
29.当时,代数式的值等于
【答案】
若x+y=1,且x≠0,则的值为____.
【答案】1
已知:x2-4x+4与互为相反数,则式子)的值等于_______.
【答案】
若a-b=ab(ab≠0),则=__.
【答案】1
33.若,则__________.
【答案】 解:∵∴∴∴∴原式.故答案是:
34.计算:=____.
【答案】.【详解】原式= =
=.故答案为:.
35.若,则的值是__________.
【答案】0或-2 【详解】设,则,,,.故,.若,则;
若,则.
解答题(共9题;共50分)
36计算:.
解:原式.?
37.计算:.
解:原式,,.??
38.先化简,再求值:(),其中a=2.
【答案】,4
【详解】()
,当a=2时,原式.
39.先化简,再求值:,在1,2,3三个数中选一个恰当的数,代入求值.
【答案】,.
【详解】原式
根据分式有意义的条件得,且则将代入得,原式.
已知,试求的值.
解:
探索:
(1)如果=3+,则m= 1 ;
(2)如果=5+,则m= ﹣13 ;
总结:如果=a+(其中a、b、c为常数),则m b﹣ac ;
应用:利用上述结论解决:若代数式的值为整数,求满足条件的整数x的值.
解:探索:(1)已知等式整理得: =,即3x+4=3x+3+m,
解得:m=1;故答案为:1;﹣13
(2)已知等式整理得: =,即5x﹣3=5x+10+m,
解得:m=﹣13;总结:m=b﹣ac; 故答案为:m=b﹣ac;
应用: ==4+,∵x为整数且为整数,∴x﹣1=±1,
∴x=2或0.
42.已知a,b,c均为非零实数,且满足==,求:的值.
解:∵==,∴=1,
∴===1,∴a+b﹣c=c,a﹣b+c=b,﹣a+b+c=a,
即a+b=2c,a+c=2b,b+c=2a,∴==8.
43.观察下列各组式子:
①;②;③
(1)请根据上面的规律写出第 个式子;
(2)请写出第个式子,并证明你发现的规律.
【答案】(1);(2),证明
【详解】(1)(2)
证明:等式左边,
∵等式右边为,与等式左边计算出的结果相等,
∴成立.
44.不等于0的三个数、、满足,求证:、、中至少有两个互为相反数.
【详解】①若,则∴.∴.∴.∴.∴或.
②若,则、互为相反数综上所述、、中必有两个互为相反数.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
