2020-2021学年九年级数学北师大版下册:3.3 垂径定理 同步练习题(word版,含答案)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版下册:3.3 垂径定理 同步练习题(word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 171.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 09:28:32 | ||
图片预览



文档简介
2020-2021学年北师大版九年级数学下册第三章
3.3
垂径定理
同步练习题
A组(基础题)
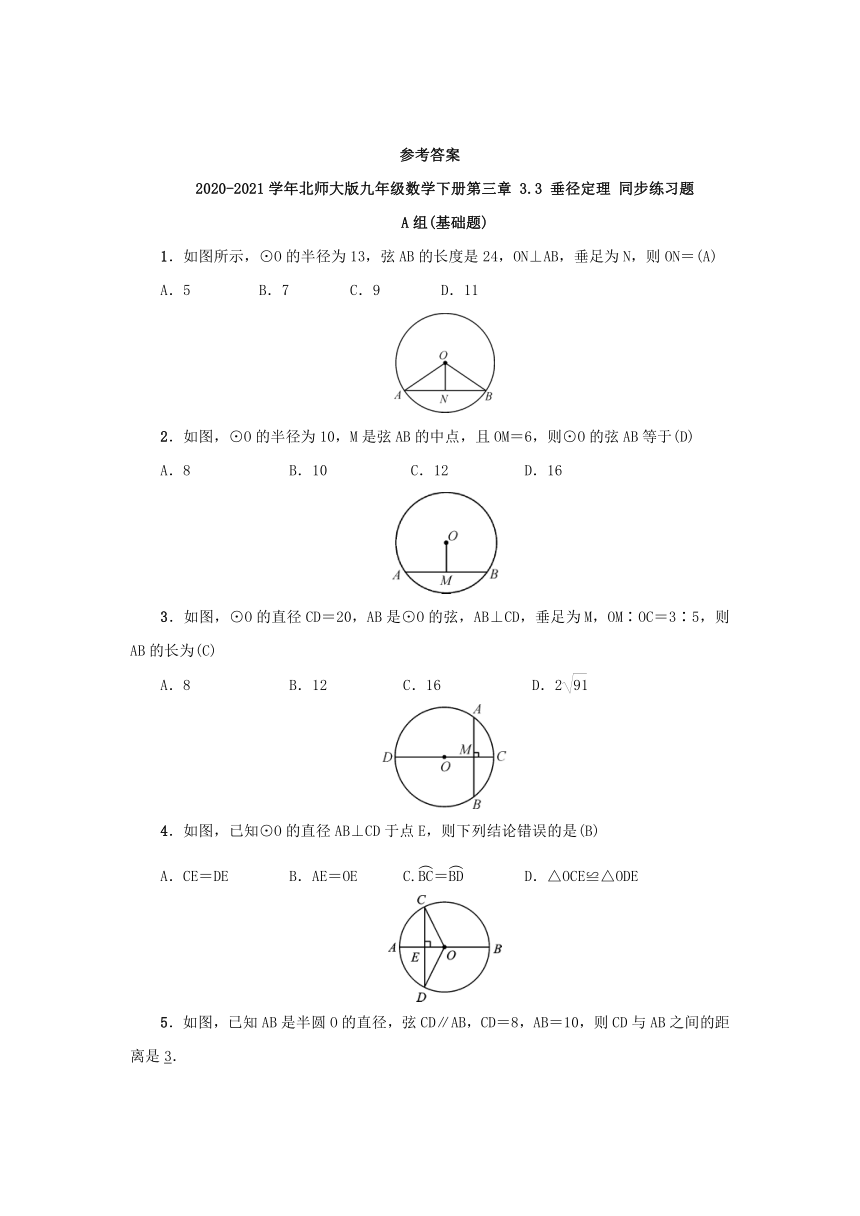
1.如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=(
)
A.5
B.7
C.9
D.11
2.如图,⊙O的半径为10,M是弦AB的中点,且OM=6,则⊙O的弦AB等于(
)
A.8
B.10
C.12
D.16
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为(
)
A.8
B.12
C.16
D.2
4.如图,已知⊙O的直径AB⊥CD于点E,则下列结论错误的是(
)
A.CE=DE
B.AE=OE
C.=
D.△OCE≌△ODE
5.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是______.
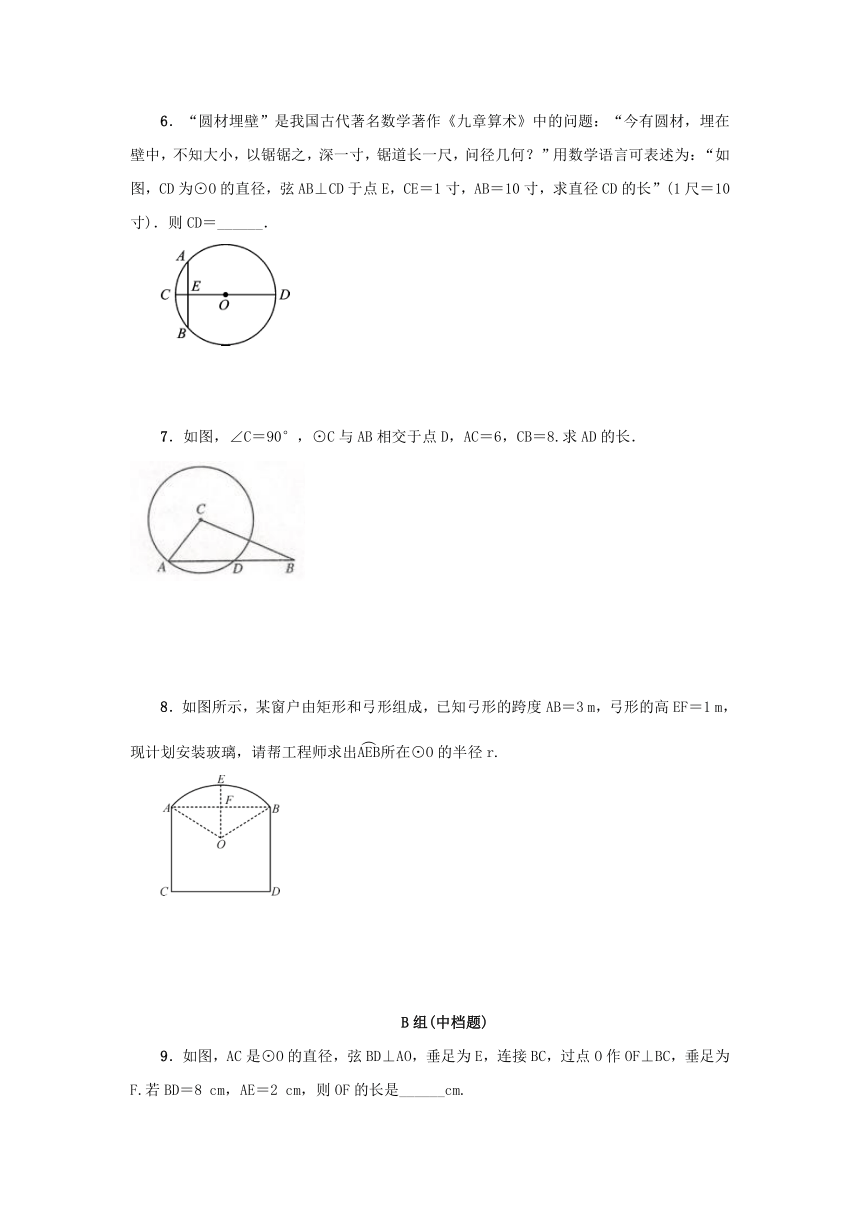
6.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,求直径CD的长”(1尺=10寸).则CD=______.
7.如图,∠C=90°,⊙C与AB相交于点D,AC=6,CB=8.求AD的长.
8.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3
m,弓形的高EF=1
m,现计划安装玻璃,请帮工程师求出所在⊙O的半径r.
B组(中档题)
9.如图,AC是⊙O的直径,弦BD⊥AO,垂足为E,连接BC,过点O作OF⊥BC,垂足为F.若BD=8
cm,AE=2
cm,则OF的长是______cm.
10.已知⊙O的半径为10
cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16
cm,CD=12
cm,则弦AB和CD之间的距离是______cm.
11.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.
12.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
13.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,问此货船能顺利通过拱桥吗?
C组(综合题)
14.如图,在Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于点D,E,F,G.
(1)求证:CD=EF;
(2)若⊙O的半径为4,AE=2,求AB的长.
参考答案
2020-2021学年北师大版九年级数学下册第三章
3.3
垂径定理
同步练习题
A组(基础题)
1.如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=(A)
A.5
B.7
C.9
D.11
2.如图,⊙O的半径为10,M是弦AB的中点,且OM=6,则⊙O的弦AB等于(D)
A.8
B.10
C.12
D.16
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为(C)
A.8
B.12
C.16
D.2
4.如图,已知⊙O的直径AB⊥CD于点E,则下列结论错误的是(B)
A.CE=DE
B.AE=OE
C.=
D.△OCE≌△ODE
5.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是3.
6.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,求直径CD的长”(1尺=10寸).则CD=26寸.
7.如图,∠C=90°,⊙C与AB相交于点D,AC=6,CB=8.求AD的长.
解:作CE⊥AD于点E,
∵∠C=90°,AC=6,CB=8,
∴AB==10.
∵CE·AB=AC·BC,
∴CE==.
在Rt△ACE中,AE===.
∵CE⊥AD,∴AE=DE.
∴AD=2AE=.
8.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3
m,弓形的高EF=1
m,现计划安装玻璃,请帮工程师求出所在⊙O的半径r.
解:∵弓形的跨度AB=3
m,EF为弓形的高,
∴OE⊥AB.
∴AF=AB=
m.
∵所在⊙O的半径为r,弓形的高EF=1
m,
∴AO=r,OF=r-1.
在Rt△AOF中,AO2=AF2+OF2,
即r2=()2+(r-1)2.解得r=.
答:所在⊙O的半径r为
m.
B组(中档题)
9.如图,AC是⊙O的直径,弦BD⊥AO,垂足为E,连接BC,过点O作OF⊥BC,垂足为F.若BD=8
cm,AE=2
cm,则OF的长是cm.
10.已知⊙O的半径为10
cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16
cm,CD=12
cm,则弦AB和CD之间的距离是2或14cm.
11.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.
12.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
解:(1)证明:过点O作OE⊥AB,垂足为E,
则AE=BE,CE=DE,
∴AE-CE=BE-DE,
即AC=BD.
(2)由(1)可知,OE⊥AB,OE⊥CD,
连接OC,OA.
∵OE=6,
∴CE===2,
AE===8.
∴AC=AE-CE=8-2.
13.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,问此货船能顺利通过拱桥吗?
解:(1)连接OB.
∵OC⊥AB,
∴D为AB的中点.
∵AB=7.2
m,
∴BD=AB=3.6
m.
设OB=OC=r,则OD=(r-2.4)m.
在Rt△BOD中,根据勾股定理,得
r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥的半径为3.9
m.
(2)令船舱顶部所在直线分别与圆弧交于点M,N(N在M的右边),连接ON,连接MN,交CO于点E.
∵CD=2.4
m,船舱顶部为长方形并高出水面2
m,∴CE=2.4-2=0.4(m).
∴OE=r-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96(m2),
∴EN=
m,
MN=2EN=2×≈3.44(m)>3
m.
∴此货船能顺利通过这座拱桥.
C组(综合题)
14.如图,在Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于点D,E,F,G.
(1)求证:CD=EF;
(2)若⊙O的半径为4,AE=2,求AB的长.
解:(1)证明:作OM⊥AB于点M,ON⊥AC于点N,OH⊥CG于点H,连接OE,OD,
∵点O为△ABC的角平分线交点,
∴OM=ON.
∵OE=OD=OC,
∴Rt△OME≌Rt△OND(HL).
∴ME=ND.
∵EF=2ME,CD=2ND,
∴CD=EF.
(2)∵点O为△ABC的角平分线交点,
∴OM=ON=OH.
∵∠ACB=90°,
∴四边形ONCH是正方形.
∴CN=CH=CD=CG=EF.
∵OC=4,
∴CH=OC=4.
∴EF=CD=CG=8.
易证得AM=AN=6,BM=BH,
∴AC=10.
设BM=BH=x,则BC=x+4,AB=x+6,
∵∠ACB=90°,
∴AB2=AC2+BC2,即(6+x)2=102+(4+x)2,
解得x=20.
∴AB=26.
3.3
垂径定理
同步练习题
A组(基础题)
1.如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=(
)
A.5
B.7
C.9
D.11
2.如图,⊙O的半径为10,M是弦AB的中点,且OM=6,则⊙O的弦AB等于(
)
A.8
B.10
C.12
D.16
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为(
)
A.8
B.12
C.16
D.2
4.如图,已知⊙O的直径AB⊥CD于点E,则下列结论错误的是(
)
A.CE=DE
B.AE=OE
C.=
D.△OCE≌△ODE
5.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是______.
6.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,求直径CD的长”(1尺=10寸).则CD=______.
7.如图,∠C=90°,⊙C与AB相交于点D,AC=6,CB=8.求AD的长.
8.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3
m,弓形的高EF=1
m,现计划安装玻璃,请帮工程师求出所在⊙O的半径r.
B组(中档题)
9.如图,AC是⊙O的直径,弦BD⊥AO,垂足为E,连接BC,过点O作OF⊥BC,垂足为F.若BD=8
cm,AE=2
cm,则OF的长是______cm.
10.已知⊙O的半径为10
cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16
cm,CD=12
cm,则弦AB和CD之间的距离是______cm.
11.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.
12.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
13.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,问此货船能顺利通过拱桥吗?
C组(综合题)
14.如图,在Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于点D,E,F,G.
(1)求证:CD=EF;
(2)若⊙O的半径为4,AE=2,求AB的长.
参考答案
2020-2021学年北师大版九年级数学下册第三章
3.3
垂径定理
同步练习题
A组(基础题)
1.如图所示,⊙O的半径为13,弦AB的长度是24,ON⊥AB,垂足为N,则ON=(A)
A.5
B.7
C.9
D.11
2.如图,⊙O的半径为10,M是弦AB的中点,且OM=6,则⊙O的弦AB等于(D)
A.8
B.10
C.12
D.16
3.如图,⊙O的直径CD=20,AB是⊙O的弦,AB⊥CD,垂足为M,OM∶OC=3∶5,则AB的长为(C)
A.8
B.12
C.16
D.2
4.如图,已知⊙O的直径AB⊥CD于点E,则下列结论错误的是(B)
A.CE=DE
B.AE=OE
C.=
D.△OCE≌△ODE
5.如图,已知AB是半圆O的直径,弦CD∥AB,CD=8,AB=10,则CD与AB之间的距离是3.
6.“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于点E,CE=1寸,AB=10寸,求直径CD的长”(1尺=10寸).则CD=26寸.
7.如图,∠C=90°,⊙C与AB相交于点D,AC=6,CB=8.求AD的长.
解:作CE⊥AD于点E,
∵∠C=90°,AC=6,CB=8,
∴AB==10.
∵CE·AB=AC·BC,
∴CE==.
在Rt△ACE中,AE===.
∵CE⊥AD,∴AE=DE.
∴AD=2AE=.
8.如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3
m,弓形的高EF=1
m,现计划安装玻璃,请帮工程师求出所在⊙O的半径r.
解:∵弓形的跨度AB=3
m,EF为弓形的高,
∴OE⊥AB.
∴AF=AB=
m.
∵所在⊙O的半径为r,弓形的高EF=1
m,
∴AO=r,OF=r-1.
在Rt△AOF中,AO2=AF2+OF2,
即r2=()2+(r-1)2.解得r=.
答:所在⊙O的半径r为
m.
B组(中档题)
9.如图,AC是⊙O的直径,弦BD⊥AO,垂足为E,连接BC,过点O作OF⊥BC,垂足为F.若BD=8
cm,AE=2
cm,则OF的长是cm.
10.已知⊙O的半径为10
cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16
cm,CD=12
cm,则弦AB和CD之间的距离是2或14cm.
11.如图,在⊙O中,弦AB=1,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为.
12.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
解:(1)证明:过点O作OE⊥AB,垂足为E,
则AE=BE,CE=DE,
∴AE-CE=BE-DE,
即AC=BD.
(2)由(1)可知,OE⊥AB,OE⊥CD,
连接OC,OA.
∵OE=6,
∴CE===2,
AE===8.
∴AC=AE-CE=8-2.
13.如图,某地有一座圆弧形拱桥,桥下水面宽度AB为7.2
m,拱高CD为2.4
m.
(1)求拱桥的半径;
(2)现有一艘宽3
m,船舱顶部为长方形并高出水面2
m的货船要经过这里,问此货船能顺利通过拱桥吗?
解:(1)连接OB.
∵OC⊥AB,
∴D为AB的中点.
∵AB=7.2
m,
∴BD=AB=3.6
m.
设OB=OC=r,则OD=(r-2.4)m.
在Rt△BOD中,根据勾股定理,得
r2=(r-2.4)2+3.62,解得r=3.9.
∴拱桥的半径为3.9
m.
(2)令船舱顶部所在直线分别与圆弧交于点M,N(N在M的右边),连接ON,连接MN,交CO于点E.
∵CD=2.4
m,船舱顶部为长方形并高出水面2
m,∴CE=2.4-2=0.4(m).
∴OE=r-CE=3.9-0.4=3.5(m).
在Rt△OEN中,EN2=ON2-OE2=3.92-3.52=2.96(m2),
∴EN=
m,
MN=2EN=2×≈3.44(m)>3
m.
∴此货船能顺利通过这座拱桥.
C组(综合题)
14.如图,在Rt△ABC中,∠ACB=90°,O为△ABC角平分线的交点,以OC为半径的⊙O交△ABC于点D,E,F,G.
(1)求证:CD=EF;
(2)若⊙O的半径为4,AE=2,求AB的长.
解:(1)证明:作OM⊥AB于点M,ON⊥AC于点N,OH⊥CG于点H,连接OE,OD,
∵点O为△ABC的角平分线交点,
∴OM=ON.
∵OE=OD=OC,
∴Rt△OME≌Rt△OND(HL).
∴ME=ND.
∵EF=2ME,CD=2ND,
∴CD=EF.
(2)∵点O为△ABC的角平分线交点,
∴OM=ON=OH.
∵∠ACB=90°,
∴四边形ONCH是正方形.
∴CN=CH=CD=CG=EF.
∵OC=4,
∴CH=OC=4.
∴EF=CD=CG=8.
易证得AM=AN=6,BM=BH,
∴AC=10.
设BM=BH=x,则BC=x+4,AB=x+6,
∵∠ACB=90°,
∴AB2=AC2+BC2,即(6+x)2=102+(4+x)2,
解得x=20.
∴AB=26.
