六年级数学下册课件-2.9整理与练习苏教版21页
文档属性
| 名称 | 六年级数学下册课件-2.9整理与练习苏教版21页 |  | |
| 格式 | zip | ||
| 文件大小 | 924.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 07:47:30 | ||
图片预览




文档简介
(共21张PPT)
圆柱、圆锥的整理和复习
点
线
面
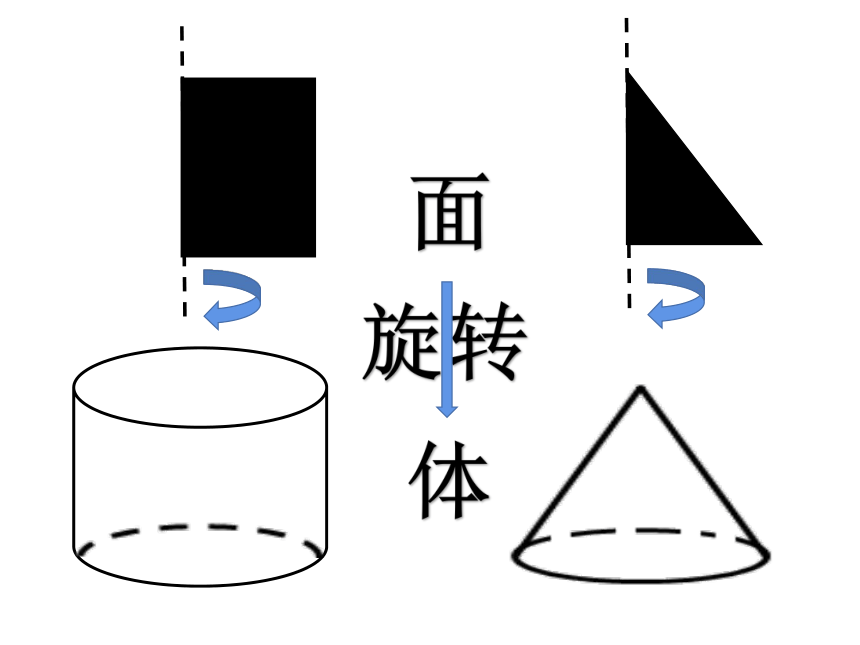
旋转
面
体
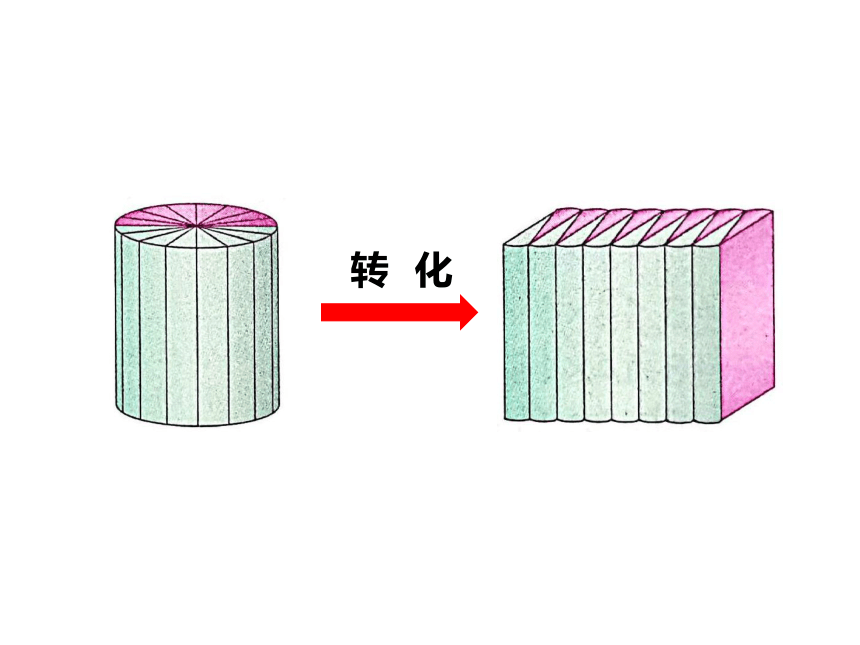
转
化
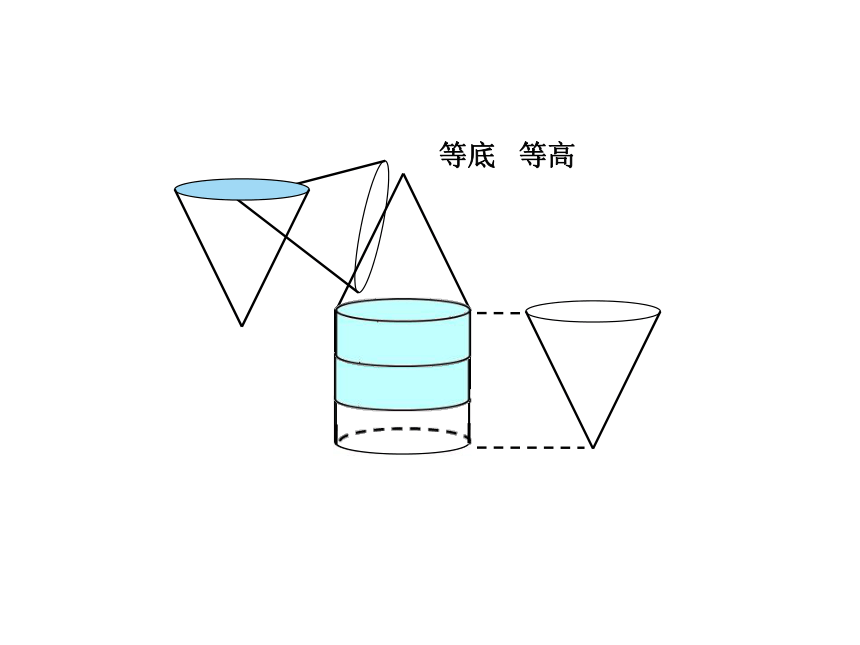
等底
等高
某种椰浆罐的形状为圆柱体。
1、把这个椰浆罐放在桌面上,占多大的面积?
2、给这个椰浆罐的侧面贴上商标纸,商标纸的面积是多少?
3、做这样一个椰浆罐需要多少铁皮?
4、这个椰浆罐最多能装多少毫升椰浆?
底面积
侧面积
表面积
容
积
题组一:只列式不计算
某种椰浆罐的形状为圆柱体,底面直径是7cm,高是11cm。(罐边厚度忽略不计)
1、把这个椰浆罐放在桌面上,占多大的面积?
2、给这个椰浆罐的侧面贴上商标纸,商标纸的面积是多少?
3、做这样一个椰浆罐需要多少铁皮?
4、这个椰浆罐最多能装多少毫升椰浆?
(7÷2)?×3.14
7×3.14×11
(7÷2)?×3.14×2+7×3.14×11
(7÷2)?×3.14×11
温馨提示:
生活问题
数学问题
转化
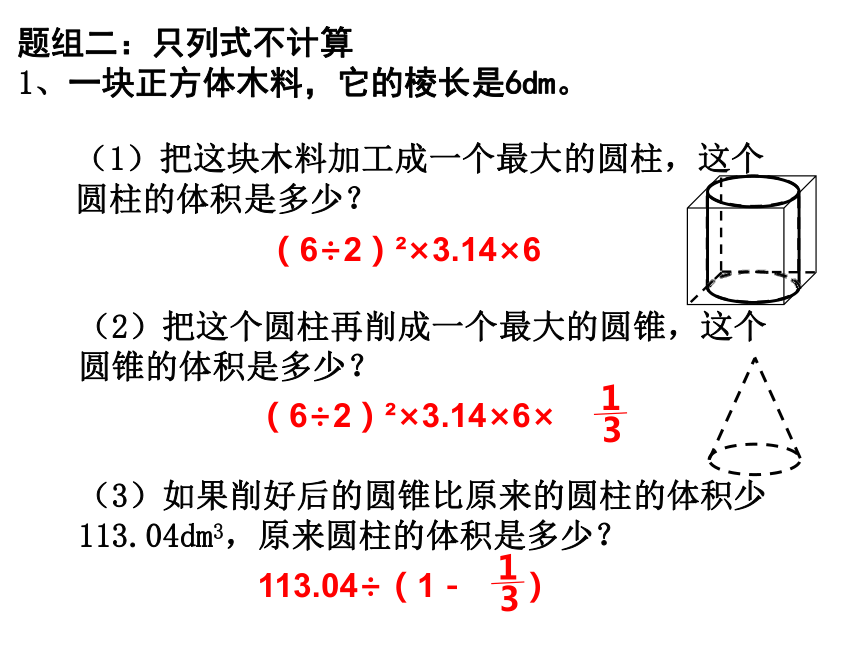
题组二:只列式不计算
1、一块正方体木料,它的棱长是6dm。
(2)把这个圆柱再削成一个最大的圆锥,这个圆锥的体积是多少?
(3)如果削好后的圆锥比原来的圆柱的体积少113.04dm3,原来圆柱的体积是多少?
(1)把这块木料加工成一个最大的圆柱,这个圆柱的体积是多少?
(6÷2)?×3.14×6
(6÷2)?×3.14×6×
1
3
113.04÷(1-
)
1
3
题组二:只列式不计算
2、
(2)一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26
cm2,圆柱的底面积是多少?
(1)一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
?
等底等高的情况下:
?
4dm
V柱
=
3V锥
若等高
?
?
?
已知:等底
已知:体积相等
4dm
若等底
?
?
已知:等高
已知:体积相等
V柱
=
V锥
V锥=V柱
?
?
3h柱
=
h锥
(1)
(2)
题组二:只列式不计算
2、
(2)一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26
cm2,圆柱的底面积是多少?
(1)一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
?
等底等高的情况下:
?
4×3
28.26÷3
当圆柱和圆锥的底面积和体积分别相等时,圆锥的
高是圆柱的3倍。
当圆柱和圆锥的体积和高分别相等时,圆柱的
底面积是圆锥的
。
1
3
题组三:
1、一个长5dm,宽3dm,高4dm的长方体水缸。水缸装满水,投入一个半径为1dm、高3dm的圆锥体铁块,缸里的水溢出多少升?
2、一瓶内直径是6cm的水瓶。水的高度是12cm,把瓶盖拧紧后倒置放平,无水部分高度10cm
。这个瓶子的容积是多少?
题组三:
1、一个长5dm,宽3dm,高4dm的长方体水缸。水缸装满水,投入一个半径为1dm、高3dm的圆锥体铁块,缸里的水溢出多少升?
5dm
3dm
4dm
5dm
3dm
4dm
溢出的水的体积
1?×3.14×3×
1
3
题组三:
2、一瓶内直径是6cm的水瓶。水的高度是12cm,把瓶盖拧紧后倒置放平,无水部分高度10cm
。这个瓶子的容积是多少?
10cm
6cm
12cm
(6÷2)?×3.14×12+(6÷2)?×3.14×10
或(6÷2)?×3.14×(12+10)
题组三:
10cm
6cm
12cm
6cm
12cm
10cm
变形前
变形后
转化
等积变形
生活问题
数学问题
计算问题
3.14×32×2+3.14×32×8
=3.14×18+3.14×72
=3.14×90
=282.6
若第一二步的计算不在口算范围,可以计算结果用带π的代数式表示,这样π还是能够放到最后才计算,减少计算量。
计算小技巧:
方法1:背诵3.14×1=
3.14×2=
······
3.14×9=
方法2:计算时圆周率∏放到最后才进行计算。
如:
方法3:若步数比较多,可适当分步解答。
温馨提示:
运用技巧
计算简便
这
节
课
你
有
什
么
收
获?
作业
完成书本第38页第1、2、3、5题
圆柱、圆锥的整理和复习
点
线
面
旋转
面
体
转
化
等底
等高
某种椰浆罐的形状为圆柱体。
1、把这个椰浆罐放在桌面上,占多大的面积?
2、给这个椰浆罐的侧面贴上商标纸,商标纸的面积是多少?
3、做这样一个椰浆罐需要多少铁皮?
4、这个椰浆罐最多能装多少毫升椰浆?
底面积
侧面积
表面积
容
积
题组一:只列式不计算
某种椰浆罐的形状为圆柱体,底面直径是7cm,高是11cm。(罐边厚度忽略不计)
1、把这个椰浆罐放在桌面上,占多大的面积?
2、给这个椰浆罐的侧面贴上商标纸,商标纸的面积是多少?
3、做这样一个椰浆罐需要多少铁皮?
4、这个椰浆罐最多能装多少毫升椰浆?
(7÷2)?×3.14
7×3.14×11
(7÷2)?×3.14×2+7×3.14×11
(7÷2)?×3.14×11
温馨提示:
生活问题
数学问题
转化
题组二:只列式不计算
1、一块正方体木料,它的棱长是6dm。
(2)把这个圆柱再削成一个最大的圆锥,这个圆锥的体积是多少?
(3)如果削好后的圆锥比原来的圆柱的体积少113.04dm3,原来圆柱的体积是多少?
(1)把这块木料加工成一个最大的圆柱,这个圆柱的体积是多少?
(6÷2)?×3.14×6
(6÷2)?×3.14×6×
1
3
113.04÷(1-
)
1
3
题组二:只列式不计算
2、
(2)一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26
cm2,圆柱的底面积是多少?
(1)一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
?
等底等高的情况下:
?
4dm
V柱
=
3V锥
若等高
?
?
?
已知:等底
已知:体积相等
4dm
若等底
?
?
已知:等高
已知:体积相等
V柱
=
V锥
V锥=V柱
?
?
3h柱
=
h锥
(1)
(2)
题组二:只列式不计算
2、
(2)一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26
cm2,圆柱的底面积是多少?
(1)一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
?
等底等高的情况下:
?
4×3
28.26÷3
当圆柱和圆锥的底面积和体积分别相等时,圆锥的
高是圆柱的3倍。
当圆柱和圆锥的体积和高分别相等时,圆柱的
底面积是圆锥的
。
1
3
题组三:
1、一个长5dm,宽3dm,高4dm的长方体水缸。水缸装满水,投入一个半径为1dm、高3dm的圆锥体铁块,缸里的水溢出多少升?
2、一瓶内直径是6cm的水瓶。水的高度是12cm,把瓶盖拧紧后倒置放平,无水部分高度10cm
。这个瓶子的容积是多少?
题组三:
1、一个长5dm,宽3dm,高4dm的长方体水缸。水缸装满水,投入一个半径为1dm、高3dm的圆锥体铁块,缸里的水溢出多少升?
5dm
3dm
4dm
5dm
3dm
4dm
溢出的水的体积
1?×3.14×3×
1
3
题组三:
2、一瓶内直径是6cm的水瓶。水的高度是12cm,把瓶盖拧紧后倒置放平,无水部分高度10cm
。这个瓶子的容积是多少?
10cm
6cm
12cm
(6÷2)?×3.14×12+(6÷2)?×3.14×10
或(6÷2)?×3.14×(12+10)
题组三:
10cm
6cm
12cm
6cm
12cm
10cm
变形前
变形后
转化
等积变形
生活问题
数学问题
计算问题
3.14×32×2+3.14×32×8
=3.14×18+3.14×72
=3.14×90
=282.6
若第一二步的计算不在口算范围,可以计算结果用带π的代数式表示,这样π还是能够放到最后才计算,减少计算量。
计算小技巧:
方法1:背诵3.14×1=
3.14×2=
······
3.14×9=
方法2:计算时圆周率∏放到最后才进行计算。
如:
方法3:若步数比较多,可适当分步解答。
温馨提示:
运用技巧
计算简便
这
节
课
你
有
什
么
收
获?
作业
完成书本第38页第1、2、3、5题
