2020-2021学年高中数学人教A版必修2单元测试卷 第一章 空间几何体 B卷 Word版含解析
文档属性
| 名称 | 2020-2021学年高中数学人教A版必修2单元测试卷 第一章 空间几何体 B卷 Word版含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 453.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览



文档简介
2020-2021学年高一数学人教A版必修2单元测试卷
第一章 空间几何体 B卷
1.一个球内有一内接长方体,其长、宽、高分别为,则球的直径为( )
A. B. C. D.
2.下列几何体中轴截面是圆面的是( )
A.圆柱??????? B.圆锥????? ??C.球????????? D.圆台
3.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所形成的几何体包括(?? )
A.一个圆台、两个圆锥????????????????? B.两个圆台、一个圆柱
C.两个圆台、一个圆锥????????????????? D.一个圆柱、两个圆锥
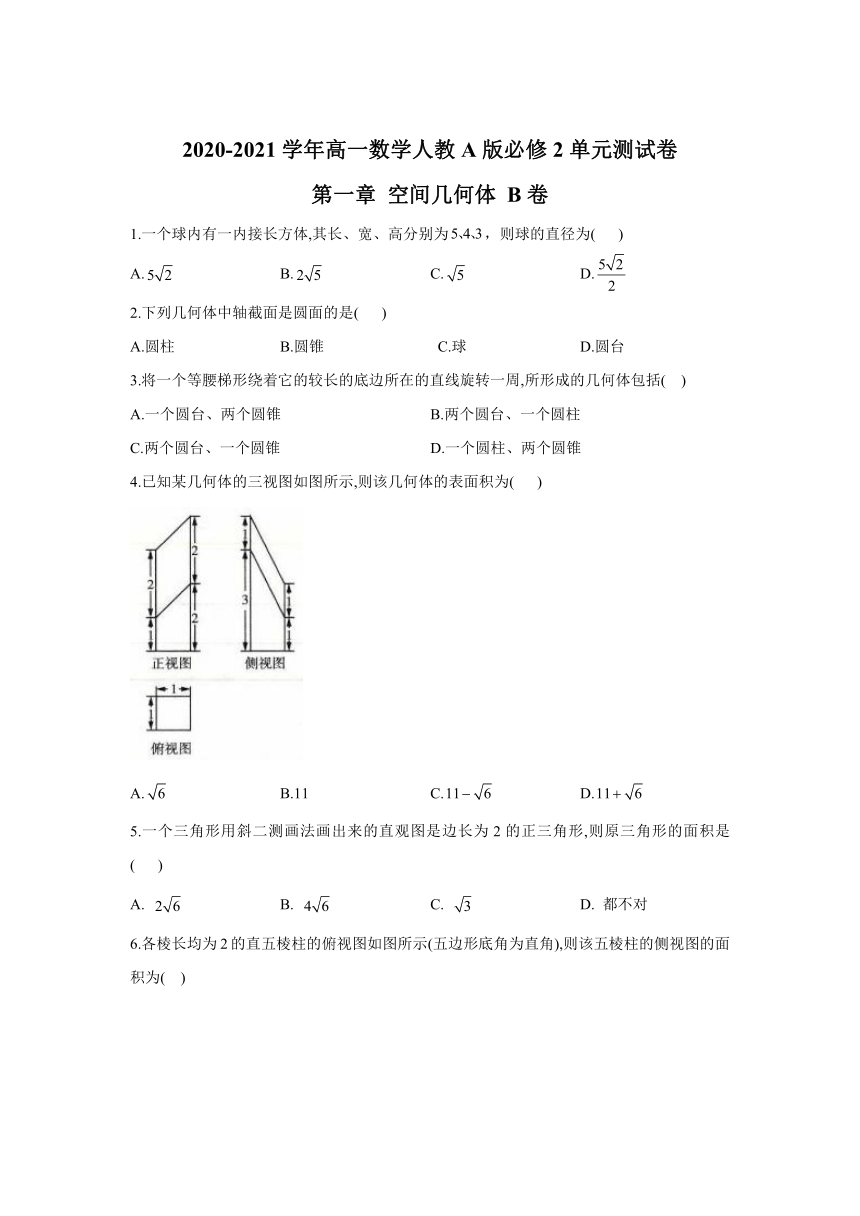
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )
A. B.11 C. D.
5.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是( )
A. B. C. D. 都不对
6.各棱长均为2的直五棱柱的俯视图如图所示(五边形底角为直角),则该五棱柱的侧视图的面积为( )
A.8 B. C. D.
7.在三棱柱中,平面是边长为2的正三角形,异面直线与所成的角为90°,则三棱柱,的体积为( )
A. B. C. D.
8.已知圆锥顶点为,底面的中心为,过直线的平面截该圆锥所得的截面是
面积为的正三角形,则该圆锥的体积为( )
A. B. C. D.
9.已知三棱锥中,,,,,,则三棱锥的体积是( )
A.4 B.6 C. D.
10.已知一个正方形的直观图是一个平行四边形,其中一条边的长为4,则正方形的面积是(?? )
A.16?????????B.64?????????C.16或64?????D.都不对
11.已知三棱锥的棱两两垂直,且长度都为,以顶点为球心,以2为半径作一个球,则球面与三棱锥的表面相交所得到的四段弧长之和等于_____.
12.某简单组合体的三视图如图所示,其中正视图与侧视图相同(尺寸如图,单位: ),则该组合体的体积是__________ (结果保留).
13.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________.
14.一个圆柱和一个圆锥的轴截面分别是边长为的正方形和边长为的正三角形,则它们的表面积之比为__________.
15.某几何体的三视图如图所示:
1.求该几何体的表面积;
2.求该几何体的体积.
答案以及解析
1.答案:A
解析:因为一个球内有一内接长方体,所以该球的直径为内接长方体的对角线,
因为内接长方体的长、宽。高分别为,所以长方体的对角线长为,所以该球的直径为.综上所述,答案选择:A
2.答案:C
解析:圆柱、圆锥、圆台的轴截面都不是圆,分别是矩形,等腰三角形和等腰梯形.
3.答案:D
解析:如图所示:
4.答案:D
解析:由三视图还原该几何体的直观图如图所示,其中四边形为平行四边形,连接,易知,所以,所以该几何体的表面积为.
5.答案:A
解析:∵三角形在其直观图中对应一个边长为2正三角形,
∴直观图的面积是
由斜二测画法中直观图和原图的面积的关系,
∴原三角形的面积为,
6.答案:B
解析:由俯视图可知侧视图是宽为,高为2的矩形,所以侧视图面积为,选B.
7.答案:C
解析:如图,连接,交于点O,则O是和的中点,取的中点D,连接,则,因为,所以.设三棱柱的高为h,则,,,因为,所以,所以三棱柱的体积,故选C.
8.答案:B
解析:∵过直线的平面截该圆锥所得的截面是面积为的正三角形,设正三角形边长为a,则,解得,所以圆锥的高为3,底面圆的直径为,所以该圆锥的体积为.
9.答案:C
解析:由,,,得.由,,,得,则,得,又,所以平面.所以三棱锥的体积为.
10.答案:C
解析:在直观图中,若长为4的边与轴平行,则正方形的边长为4,此时面积为16,若长为4的边与轴平行,则正方形的边长为8,此时面积为64.
11.答案:
解析:如图所示,为等腰直角三角形,且.以顶点为球心,以2为半径作一个球与的分别交于,得,,所以,∴,同理.是以顶点为圆心,以2为半径的圆周长的,所以,球面与三棱锥的表面相交所得到的四段弧长之和等于.
故答案为:.
12.答案:
解析:
由题知该组合体的底部为正四棱柱,上部为圆锥,其中四棱柱的底面边长为,高为,圆锥的底面圆半径为1,高为1,故该组合体的体积为.
13.答案:
解析:由三棱锥的正视图知,三棱锥的高为1,底面边长为,2,2,则底面等腰三角形的顶角为120°,所以三棱锥的体积为.
14.答案:2:1
解析:由题意,得圆柱的表面积
圆锥的表面积
所以面积比圆柱面积比圆锥面积为2:1
15.答案:1.由三视图知,此几何体由上下两部分组成,其中上边是一个半径为1的半球,下边是一个棱长为2的正方体。
2.
第一章 空间几何体 B卷
1.一个球内有一内接长方体,其长、宽、高分别为,则球的直径为( )
A. B. C. D.
2.下列几何体中轴截面是圆面的是( )
A.圆柱??????? B.圆锥????? ??C.球????????? D.圆台
3.将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所形成的几何体包括(?? )
A.一个圆台、两个圆锥????????????????? B.两个圆台、一个圆柱
C.两个圆台、一个圆锥????????????????? D.一个圆柱、两个圆锥
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )
A. B.11 C. D.
5.一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是( )
A. B. C. D. 都不对
6.各棱长均为2的直五棱柱的俯视图如图所示(五边形底角为直角),则该五棱柱的侧视图的面积为( )
A.8 B. C. D.
7.在三棱柱中,平面是边长为2的正三角形,异面直线与所成的角为90°,则三棱柱,的体积为( )
A. B. C. D.
8.已知圆锥顶点为,底面的中心为,过直线的平面截该圆锥所得的截面是
面积为的正三角形,则该圆锥的体积为( )
A. B. C. D.
9.已知三棱锥中,,,,,,则三棱锥的体积是( )
A.4 B.6 C. D.
10.已知一个正方形的直观图是一个平行四边形,其中一条边的长为4,则正方形的面积是(?? )
A.16?????????B.64?????????C.16或64?????D.都不对
11.已知三棱锥的棱两两垂直,且长度都为,以顶点为球心,以2为半径作一个球,则球面与三棱锥的表面相交所得到的四段弧长之和等于_____.
12.某简单组合体的三视图如图所示,其中正视图与侧视图相同(尺寸如图,单位: ),则该组合体的体积是__________ (结果保留).
13.已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是__________.
14.一个圆柱和一个圆锥的轴截面分别是边长为的正方形和边长为的正三角形,则它们的表面积之比为__________.
15.某几何体的三视图如图所示:
1.求该几何体的表面积;
2.求该几何体的体积.
答案以及解析
1.答案:A
解析:因为一个球内有一内接长方体,所以该球的直径为内接长方体的对角线,
因为内接长方体的长、宽。高分别为,所以长方体的对角线长为,所以该球的直径为.综上所述,答案选择:A
2.答案:C
解析:圆柱、圆锥、圆台的轴截面都不是圆,分别是矩形,等腰三角形和等腰梯形.
3.答案:D
解析:如图所示:
4.答案:D
解析:由三视图还原该几何体的直观图如图所示,其中四边形为平行四边形,连接,易知,所以,所以该几何体的表面积为.
5.答案:A
解析:∵三角形在其直观图中对应一个边长为2正三角形,
∴直观图的面积是
由斜二测画法中直观图和原图的面积的关系,
∴原三角形的面积为,
6.答案:B
解析:由俯视图可知侧视图是宽为,高为2的矩形,所以侧视图面积为,选B.
7.答案:C
解析:如图,连接,交于点O,则O是和的中点,取的中点D,连接,则,因为,所以.设三棱柱的高为h,则,,,因为,所以,所以三棱柱的体积,故选C.
8.答案:B
解析:∵过直线的平面截该圆锥所得的截面是面积为的正三角形,设正三角形边长为a,则,解得,所以圆锥的高为3,底面圆的直径为,所以该圆锥的体积为.
9.答案:C
解析:由,,,得.由,,,得,则,得,又,所以平面.所以三棱锥的体积为.
10.答案:C
解析:在直观图中,若长为4的边与轴平行,则正方形的边长为4,此时面积为16,若长为4的边与轴平行,则正方形的边长为8,此时面积为64.
11.答案:
解析:如图所示,为等腰直角三角形,且.以顶点为球心,以2为半径作一个球与的分别交于,得,,所以,∴,同理.是以顶点为圆心,以2为半径的圆周长的,所以,球面与三棱锥的表面相交所得到的四段弧长之和等于.
故答案为:.
12.答案:
解析:
由题知该组合体的底部为正四棱柱,上部为圆锥,其中四棱柱的底面边长为,高为,圆锥的底面圆半径为1,高为1,故该组合体的体积为.
13.答案:
解析:由三棱锥的正视图知,三棱锥的高为1,底面边长为,2,2,则底面等腰三角形的顶角为120°,所以三棱锥的体积为.
14.答案:2:1
解析:由题意,得圆柱的表面积
圆锥的表面积
所以面积比圆柱面积比圆锥面积为2:1
15.答案:1.由三视图知,此几何体由上下两部分组成,其中上边是一个半径为1的半球,下边是一个棱长为2的正方体。
2.
