2020-2021学年高中数学人教B版必修2单元测试卷 第一章立体几何初步 B卷 Word版含解析
文档属性
| 名称 | 2020-2021学年高中数学人教B版必修2单元测试卷 第一章立体几何初步 B卷 Word版含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 21:48:35 | ||
图片预览



文档简介
2020-2021学年高一数学人教B版必修2单元测试卷
第一章 立体几何初步 B卷
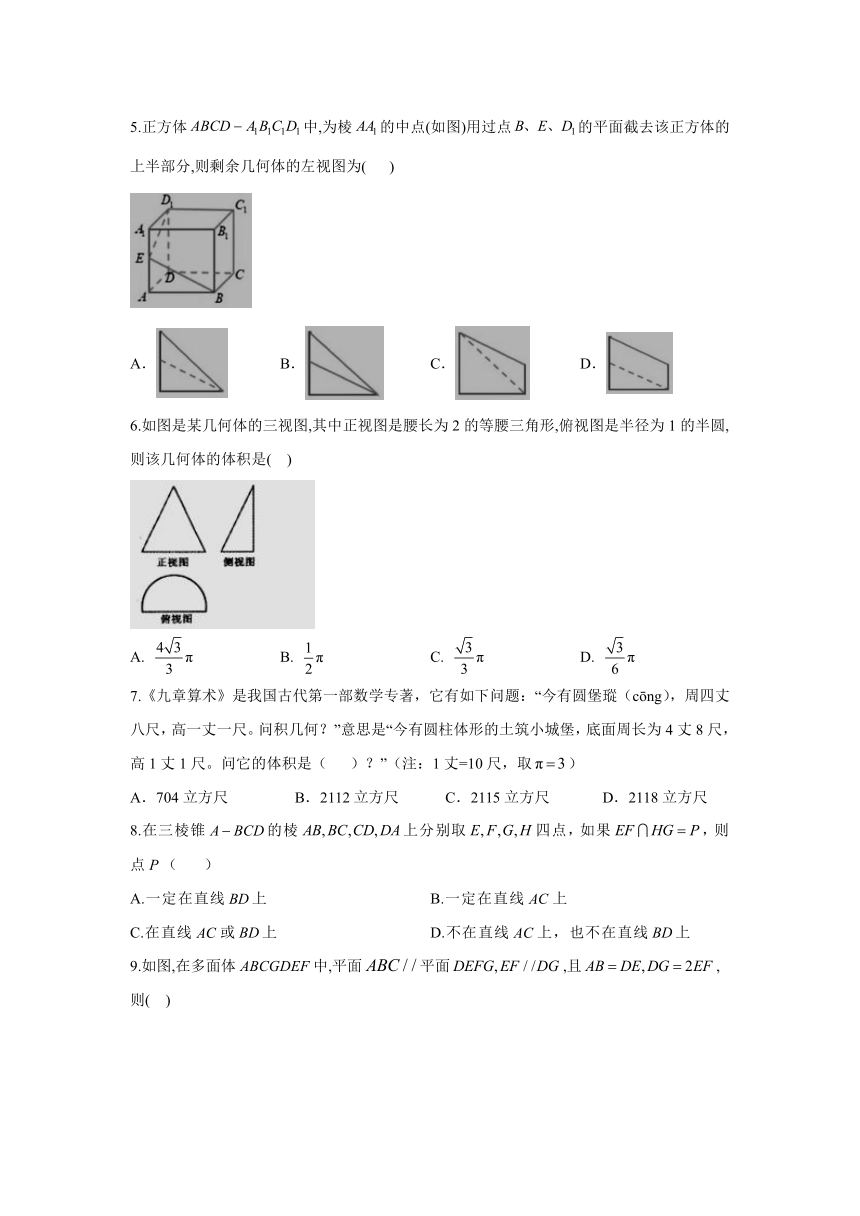
1.关于如图所示几何体的正确说法为(???)
①这是一个六面体
②这是一个四棱台
③这是一个四棱柱
④此几何体可由三棱柱截去一个三棱柱得到
⑤此几何体可由四棱柱截去一个三棱柱得到
A.①②③?????B.①③④?????C.①②④⑤?????D.①③④⑤
2.下列几何体中是棱柱的有( )
A.1个 B.2个 C.3个 D.4个
3.半径为的半圆卷成底面积最大的圆锥,所得圆锥的高为( )
A. B. C. D.
4.如图,矩形是水平放置的一个平面图形的直观图,其中,,则原图形是( )
A.正方形 B.矩形 C.菱形 D.一般的平行四边形
5.正方体中,为棱的中点(如图)用过点的平面截去该正方体的上半部分,则剩余几何体的左视图为( )
A. B. C. D.
6.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是(?? )
A. B. C. D.
7.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡瑽(cōng),周四丈八尺,高一丈一尺。问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺。问它的体积是( )?”(注:1丈=10尺,取)
A.704立方尺 B.2112立方尺 C.2115立方尺 D.2118立方尺
8.在三棱锥的棱上分别取四点,如果,则点( )
A.一定在直线上 B.一定在直线上
C.在直线或上 D.不在直线上,也不在直线上
9.如图,在多面体中,平面平面,且,则(? ?)
A. 平面
B. 平面
C.
D.平面平面
10.已知是不重合的平面,是不重合的直线,则的一个充分条件是( )
A. B.
C. D.
11.已知圆锥的母线长为,侧面积为,则此圆锥的体积为
__________ .
12.在长方体中,,若在长方体中挖去一个体积最大的圆柱,则此圆柱与原长方体的体积比为___________.
13.已知是空间中的三条相互不重合的直线,给出下列说法:
①若,则;②若a与b相交,b与c相交,则a与c相交;
③若平面a,平面β,则一定是异面直线;④若与c成等角,则.
其中正确的说法是________(填序号).
14.如图,四边形是边长为1的正方形,平面,平面,且
,G为线段上的动点,则下列结论 中正确的是 .
①;
②该几何体外接球的表面积为;
③若G为的中点,则平面
④的最小值为3.
15.如图,两两垂直,,为的中点,点在线段上,.
(1)求的长;
(2)若点在线段上,设,当时,求实数的值.
答案以及解析
1.答案:D
解析:
①正确.因为有六个面,属于六面体的范围.
②错误.因为侧棱的延长线不能交于一点,所以不正确.
③正确.如果把几何体放倒就会发现是一个四棱柱.
④⑤都正确.如图所示.
2.答案:C
解析:
观察图形得:“有两个面互相平行,其余各面都是四边形,”的几何体有:
①③⑤,只有它们是棱柱,
故答案为:①③⑤。
3.答案:B
解析:半径为的半圆弧长为,所以卷成的圆锥的底面圆的周长为,圆锥的底面半径为,所以圆锥的高为.故选B.
4.答案:C
解析:根据题意,直观图的两组对边分别平行且.
还原为平面图形是邻边不垂直,且,如图所示,
,
四边形是菱形.
故选:C.
5.答案:D
解析:由题意可知:过点的平面截去该正方体的上半部分,如图直观图,则几何体的左视图为,故选D.
6.答案:D
解析:由三视图,
可知给定的几何体是一个圆锥的一半,故所求的体积为.
7.答案:B
解析:设圆柱形城堡的底面半径为尺,高为尺,则尺,∴,
∴城堡的体积立方尺。
故选:B.
8.答案:B
解析:如图所示,∵ 平面ABC,平面ACD,,∴平面ABC,平面ACD.又∵平面平面,,故选B.
9.答案:A
解析:取的中点.连接,如图所示.
则由已知条件易证四边形是平行四边形,
∴.
∵平面平面,
平面平面,
平面平面,
∴,
∴.
又,
∴,
∴四边形是平行四边形,即.
又平面,
∴平面.
故选A.
10.答案:C
解析:对于答案A:,得出m与α是相交的或是垂直的,故A错;
答案B:,得出m与α是相交的、平行的都可以,故B错;
答案C:,得出,再得出,故C正确;
答案D:,得出m与α是相交的或是垂直的,故D错
故选C
11.答案:
解析:设圆锥的底面半径为,则,解得,
∴圆锥的,
∴圆锥的体积
故答案为.
12.答案:
解析:分别以三种面上最大圆为圆柱的底面的圆柱体积为,所以最大体积为,所以此圆柱与原长方体的体积比为.
13.答案:①
解析:由公理4知①正确;当a与b相交,b与c相交时,a与c可能相交、平行,也可能异面,故②不正确;当平面α,平面β时,a与b可能平行、相交或异面,故③不正确;当a,b与c成等角时,a与b可能相交、平行,也可能异面,故④不正确.
14.答案:①②③
解析: 如图所示,
几何体 可补形为正方体,以D为坐标原点,
所在直线分别为x轴、y 轴、z轴建立空间直角坐标系
①由 正方体的性质易得
②该几 何体的外接球与正方体的外接球相同,外接球半径为故外接球表面积为.
③,则设平面的法向量为,由得令,,则当 G为的中点时,则,所以这,可得平面(也可 由平面平行来证明线面平行).
④设,则,故当,的最小值为.
15.答案:(1)以为坐标原点,分别以的方向为轴,轴,轴的正方向建立空间直角坐标系,(图略)则
由为的中点,得,
,即的长为.
(2)设,且点在线段上,
,
.
第一章 立体几何初步 B卷
1.关于如图所示几何体的正确说法为(???)
①这是一个六面体
②这是一个四棱台
③这是一个四棱柱
④此几何体可由三棱柱截去一个三棱柱得到
⑤此几何体可由四棱柱截去一个三棱柱得到
A.①②③?????B.①③④?????C.①②④⑤?????D.①③④⑤
2.下列几何体中是棱柱的有( )
A.1个 B.2个 C.3个 D.4个
3.半径为的半圆卷成底面积最大的圆锥,所得圆锥的高为( )
A. B. C. D.
4.如图,矩形是水平放置的一个平面图形的直观图,其中,,则原图形是( )
A.正方形 B.矩形 C.菱形 D.一般的平行四边形
5.正方体中,为棱的中点(如图)用过点的平面截去该正方体的上半部分,则剩余几何体的左视图为( )
A. B. C. D.
6.如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是(?? )
A. B. C. D.
7.《九章算术》是我国古代第一部数学专著,它有如下问题:“今有圆堡瑽(cōng),周四丈八尺,高一丈一尺。问积几何?”意思是“今有圆柱体形的土筑小城堡,底面周长为4丈8尺,高1丈1尺。问它的体积是( )?”(注:1丈=10尺,取)
A.704立方尺 B.2112立方尺 C.2115立方尺 D.2118立方尺
8.在三棱锥的棱上分别取四点,如果,则点( )
A.一定在直线上 B.一定在直线上
C.在直线或上 D.不在直线上,也不在直线上
9.如图,在多面体中,平面平面,且,则(? ?)
A. 平面
B. 平面
C.
D.平面平面
10.已知是不重合的平面,是不重合的直线,则的一个充分条件是( )
A. B.
C. D.
11.已知圆锥的母线长为,侧面积为,则此圆锥的体积为
__________ .
12.在长方体中,,若在长方体中挖去一个体积最大的圆柱,则此圆柱与原长方体的体积比为___________.
13.已知是空间中的三条相互不重合的直线,给出下列说法:
①若,则;②若a与b相交,b与c相交,则a与c相交;
③若平面a,平面β,则一定是异面直线;④若与c成等角,则.
其中正确的说法是________(填序号).
14.如图,四边形是边长为1的正方形,平面,平面,且
,G为线段上的动点,则下列结论 中正确的是 .
①;
②该几何体外接球的表面积为;
③若G为的中点,则平面
④的最小值为3.
15.如图,两两垂直,,为的中点,点在线段上,.
(1)求的长;
(2)若点在线段上,设,当时,求实数的值.
答案以及解析
1.答案:D
解析:
①正确.因为有六个面,属于六面体的范围.
②错误.因为侧棱的延长线不能交于一点,所以不正确.
③正确.如果把几何体放倒就会发现是一个四棱柱.
④⑤都正确.如图所示.
2.答案:C
解析:
观察图形得:“有两个面互相平行,其余各面都是四边形,”的几何体有:
①③⑤,只有它们是棱柱,
故答案为:①③⑤。
3.答案:B
解析:半径为的半圆弧长为,所以卷成的圆锥的底面圆的周长为,圆锥的底面半径为,所以圆锥的高为.故选B.
4.答案:C
解析:根据题意,直观图的两组对边分别平行且.
还原为平面图形是邻边不垂直,且,如图所示,
,
四边形是菱形.
故选:C.
5.答案:D
解析:由题意可知:过点的平面截去该正方体的上半部分,如图直观图,则几何体的左视图为,故选D.
6.答案:D
解析:由三视图,
可知给定的几何体是一个圆锥的一半,故所求的体积为.
7.答案:B
解析:设圆柱形城堡的底面半径为尺,高为尺,则尺,∴,
∴城堡的体积立方尺。
故选:B.
8.答案:B
解析:如图所示,∵ 平面ABC,平面ACD,,∴平面ABC,平面ACD.又∵平面平面,,故选B.
9.答案:A
解析:取的中点.连接,如图所示.
则由已知条件易证四边形是平行四边形,
∴.
∵平面平面,
平面平面,
平面平面,
∴,
∴.
又,
∴,
∴四边形是平行四边形,即.
又平面,
∴平面.
故选A.
10.答案:C
解析:对于答案A:,得出m与α是相交的或是垂直的,故A错;
答案B:,得出m与α是相交的、平行的都可以,故B错;
答案C:,得出,再得出,故C正确;
答案D:,得出m与α是相交的或是垂直的,故D错
故选C
11.答案:
解析:设圆锥的底面半径为,则,解得,
∴圆锥的,
∴圆锥的体积
故答案为.
12.答案:
解析:分别以三种面上最大圆为圆柱的底面的圆柱体积为,所以最大体积为,所以此圆柱与原长方体的体积比为.
13.答案:①
解析:由公理4知①正确;当a与b相交,b与c相交时,a与c可能相交、平行,也可能异面,故②不正确;当平面α,平面β时,a与b可能平行、相交或异面,故③不正确;当a,b与c成等角时,a与b可能相交、平行,也可能异面,故④不正确.
14.答案:①②③
解析: 如图所示,
几何体 可补形为正方体,以D为坐标原点,
所在直线分别为x轴、y 轴、z轴建立空间直角坐标系
①由 正方体的性质易得
②该几 何体的外接球与正方体的外接球相同,外接球半径为故外接球表面积为.
③,则设平面的法向量为,由得令,,则当 G为的中点时,则,所以这,可得平面(也可 由平面平行来证明线面平行).
④设,则,故当,的最小值为.
15.答案:(1)以为坐标原点,分别以的方向为轴,轴,轴的正方向建立空间直角坐标系,(图略)则
由为的中点,得,
,即的长为.
(2)设,且点在线段上,
,
.
