第三章 圆练习题(Word版 含答案)
文档属性
| 名称 | 第三章 圆练习题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 356.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 13:46:09 | ||
图片预览



文档简介
1165860012611100第三章 圆 练习题
专题一 与圆周角有关的计算
A组(基础题)
1.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )
A.54° B.64° C.27° D.37°
2.如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为( )
A.45° B.60° C.75° D.90°
3.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD.若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.5 D.5
4.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD相交于点E.若E是BD的中点,则AC的长是( )
A. B.3 C.3 D.4
5.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB=______.
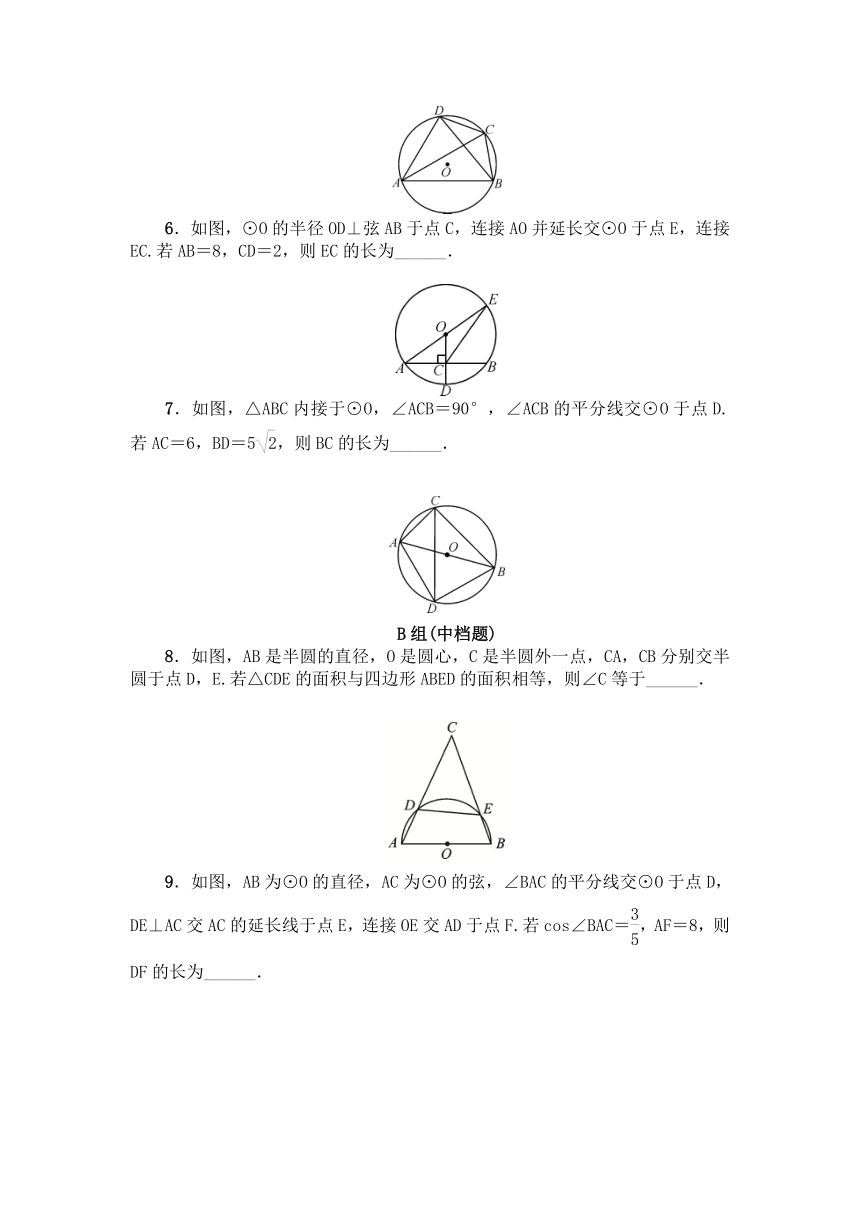
6.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为______.
7.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的平分线交⊙O于点D.若AC=6,BD=5,则BC的长为______.
B组(中档题)
8.如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA,CB分别交半圆于点D,E.若△CDE的面积与四边形ABED的面积相等,则∠C等于______.
9.如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC交AC的延长线于点E,连接OE交AD于点F.若cos∠BAC=,AF=8,则DF的长为______.
C组(综合题)
10.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB=______.
专题二 与圆有关阴影部分面积的计算
A组(基础题)
1.如图,在?ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是( )
A.π B.2π C.3π D.6π
2.如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4π-8 B.2π C.4π D.8π-8
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
A.π B.2π C.3π D.4π
4.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3π C.2π D.2π
5.如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是______.
B组(中档题)
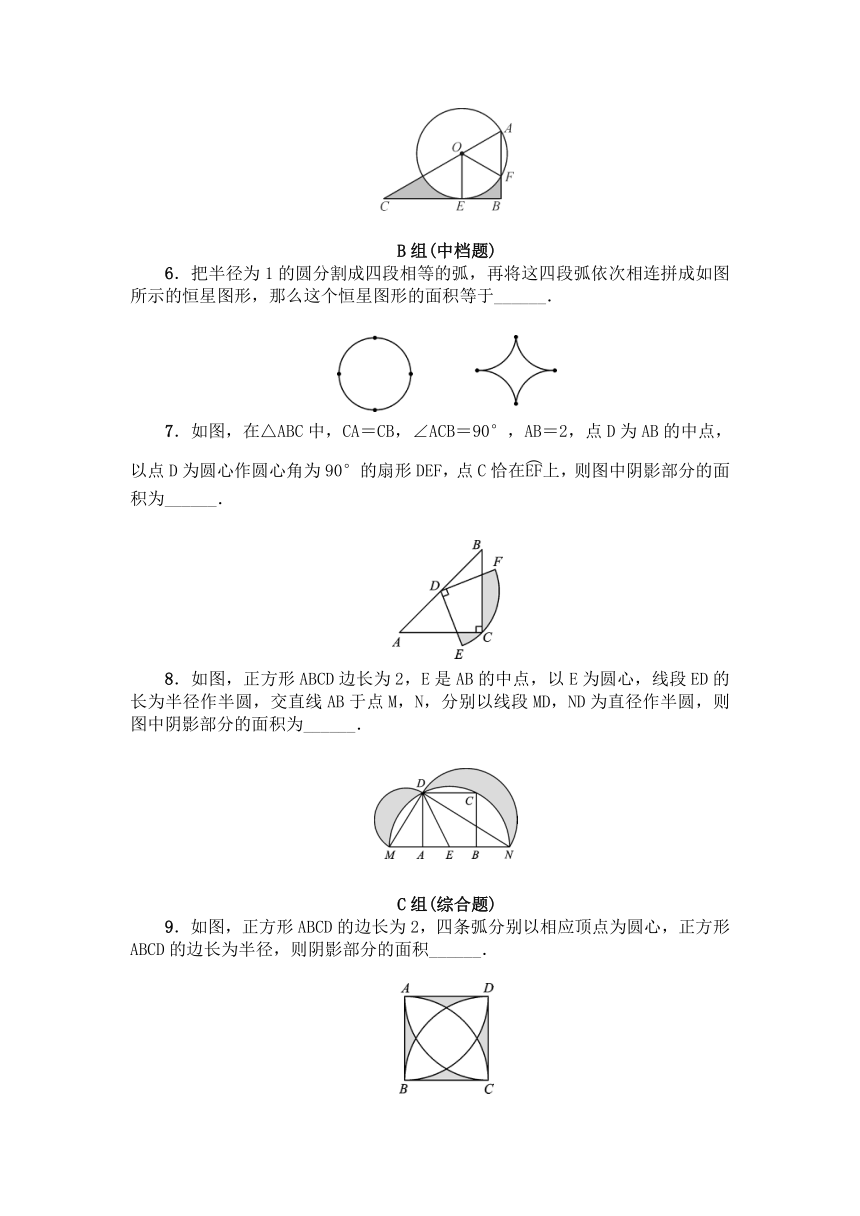
6.把半径为1的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图所示的恒星图形,那么这个恒星图形的面积等于______.
7.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为______.
8.如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N,分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为______.
C组(综合题)
9.如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径,则阴影部分的面积______.
专题三 圆与相似
1.如图,在四边形ABCD中,AB∥DC,∠B=∠D.过点C作CH⊥AB交DA的延长线于点E,设垂足为H.以CE为直径作⊙O分别交AD,BC于点F,G,连接CF,若CF=CH.
(1)求证:四边形ABCD为菱形;
(2)若tanB=,OH=9,求AE的长.
2.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连接CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
4.如图,已知在Rt△ABC中,∠ACB=90°,AC=4,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A,P是上的一个动点.
(1)求半径OB的长;
(2)如果点P是的中点,连接PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP,CA交于点D,求线段DP的长.
5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=,求DG的长.
参考答案
2020-2021学年北师大版九年级数学下册第三章 圆 章末专题复习练习题
专题一 与圆周角有关的计算
A组(基础题)
1.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=(C)
A.54° B.64° C.27° D.37°
2.(2020·绍兴)如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为(D)
A.45° B.60° C.75° D.90°
3.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD.若∠AOB与∠COD互补,弦CD=6,则弦AB的长为(B)
A.6 B.8 C.5 D.5
4.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD相交于点E.若E是BD的中点,则AC的长是(D)
A. B.3 C.3 D.4
5.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB=70°.
6.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为2.
7.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的平分线交⊙O于点D.若AC=6,BD=5,则BC的长为8.
B组(中档题)
8.如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA,CB分别交半圆于点D,E.若△CDE的面积与四边形ABED的面积相等,则∠C等于45°.
9.如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC交AC的延长线于点E,连接OE交AD于点F.若cos∠BAC=,AF=8,则DF的长为5.
C组(综合题)
10.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB=.
专题二 与圆有关阴影部分面积的计算
A组(基础题)
1.如图,在?ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是(C)
A.π B.2π C.3π D.6π
2.如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为(A)
A.4π-8 B.2π C.4π D.8π-8
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是(B)
A.π B.2π C.3π D.4π
4.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为(A)
A.6π B.3π C.2π D.2π
5.如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是-π.
B组(中档题)
6.把半径为1的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图所示的恒星图形,那么这个恒星图形的面积等于4-π.
7.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为-.
8.如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N,分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为2.
C组(综合题)
9.如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径,则阴影部分的面积16-4-π.
专题三 圆与相似
1.如图,在四边形ABCD中,AB∥DC,∠B=∠D.过点C作CH⊥AB交DA的延长线于点E,设垂足为H.以CE为直径作⊙O分别交AD,BC于点F,G,连接CF,若CF=CH.
(1)求证:四边形ABCD为菱形;
(2)若tanB=,OH=9,求AE的长.
解:(1)证明:∵AB∥CD,
∴∠D+∠DAB=180°.
∵∠B=∠D,
∴∠B+∠DAB=180°.
∴AD∥BC.
∴四边形ABCD是平行四边形.
∵CE是⊙O的直径,CH⊥AB,
∴∠CFD=90°=∠CHB.
∵CF=CH,∴△CFD≌△CHB(AAS).
∴CD=CB.∴四边形ABCD是菱形.
(2)由(1)可知,BC∥AD,CF⊥AD,
∴BC⊥CF.∴∠B=∠BAE.
∵BH=DF,AB=AD,∴AF=AH.
∵tan∠B==tan∠BAE,
∴设AH=4a,则HE=3a,AE=5a,AF=4a,EF=9a.
∵∠E=∠E,∠AHE=∠EFC=90°,
∴△EAH∽△ECF.
∴=.
∴=.
∴CE=15a.
∵OH=9,∴15a=2(3a+9).
∴a=2.
∴AE=5a=10.
2.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连接CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
解:(1)证明:连接OB,则OP=OB,
∴∠OBP=∠OPB=∠CPA.
∵AB=AC,
∴∠ACB=∠ABC.
∵OA⊥l,∴∠OAC=90°.
∴∠ACB+∠CPA=90°.
∴∠ABP+∠OBP=90°,
即∠ABO=90°.
∴OB⊥AB.
又∵OB是⊙O的半径,
∴AB是⊙O的切线.
(2)由(1)知,∠ABO=90°,
∵OA=5,OB=3,
∴由勾股定理,得AB=4.
过点O作OD⊥PB于点D,则PD=DB,
∵∠OPD=∠CPA,∠ODP=∠CAP=90°,
∴△ODP∽△CAP.
∴=.
又∵AC=AB=4,AP=OA-OP=2,
∴PC==2.
∴PD==.
∴BP=2PD=.
3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD,∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.
∴OD⊥CD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD.∴=.
∵=,BC=6,∴CD=4.
∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.
解得BE=.
4.如图,已知在Rt△ABC中,∠ACB=90°,AC=4,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A,P是上的一个动点.
(1)求半径OB的长;
(2)如果点P是的中点,连接PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP,CA交于点D,求线段DP的长.
解:(1)∵Rt△ABC中,∠ACB=90°,AC=4,BC=16,
∴AB==12.
过点O作OH⊥AB于点H,
则BH=AB=6.
∵∠BHO=∠ACB=90°,∠B=∠B,
∴△BHO∽△BCA.∴=.
∴=.∴OB=9.
(2)如图1,连接OP交AB于点H,过点P作PE⊥BC于点E,
∵点P是的中点,
∴OP⊥AB,AH=BH=AB=6.
在Rt△BHO中,OH==3.
在△POE和△BOH中,
∴△POE≌△BOH(AAS).
∴PE=HB=6,OE=OH=3.
∴CE=BC-OB+OE=10.
∴tan∠PCB==.
(3)如图2,过点A作AE⊥BD于点E,连接CP,
∵BA平分∠PBC,AC⊥BC,
∴AE=AC=4.
∵∠AED=∠ACB=90°,∠D=∠D,
∴△ADE∽△BDC.∴=.
设DE=x,∴=.∴CD=2.
在Rt△ACB和Rt△AEB中,
∴Rt△ACB≌Rt△AEB(HL).
∴BE=BC=16.
∵CD2+BC2=BD2,
∴(2)2+162=(16+x)2,解得x=.
∴BD=16+=.
∴过点O作OF⊥PB交PB于点F,
则△OBF∽△DBC,∴=.
∴=.∴BF=7.∴PB=2BF=14.
∴PD=BD-BP=.
5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=,求DG的长.
解:(1)证明:连接OD,
∵AD为∠BAC的角平分线,∴∠BAD=∠CAD.
∵OA=OD,
∴∠ODA=∠OAD.
∴∠ODA=∠CAD.
∴OD∥AC.
∵∠C=90°,∴∠ODC=90°.
∴OD⊥BC.
∵OD是⊙O的半径,∴BC是⊙O的切线.
(2)连接DF,由(1)知BC为⊙O的切线,
∴∠FDC=∠DAF.∴∠CDA=∠CFD.
∵∠BAD=∠DAF.∴△ABD∽△ADF.
∴=,即AD2=AB·AF=xy,
∴AD=.
(3)连接EF,在Rt△BOD中,sinB==,
设圆的半径为r,可得=,
解得r=5.∴AE=10,AB=18.
∵AE是直径,∴∠AFE=∠C=90°.
∴EF∥BC,∴∠AEF=∠B.
∴sin∠AEF==.
∴AF=AE·sin∠AEF=10×=.
∵AF∥OD,
∴===,即DG=AD.
由(2)知AD===,
则DG=×=.
专题一 与圆周角有关的计算
A组(基础题)
1.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=( )
A.54° B.64° C.27° D.37°
2.如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为( )
A.45° B.60° C.75° D.90°
3.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD.若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.5 D.5
4.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD相交于点E.若E是BD的中点,则AC的长是( )
A. B.3 C.3 D.4
5.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB=______.
6.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为______.
7.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的平分线交⊙O于点D.若AC=6,BD=5,则BC的长为______.
B组(中档题)
8.如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA,CB分别交半圆于点D,E.若△CDE的面积与四边形ABED的面积相等,则∠C等于______.
9.如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC交AC的延长线于点E,连接OE交AD于点F.若cos∠BAC=,AF=8,则DF的长为______.
C组(综合题)
10.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB=______.
专题二 与圆有关阴影部分面积的计算
A组(基础题)
1.如图,在?ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是( )
A.π B.2π C.3π D.6π
2.如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为( )
A.4π-8 B.2π C.4π D.8π-8
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是( )
A.π B.2π C.3π D.4π
4.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π B.3π C.2π D.2π
5.如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是______.
B组(中档题)
6.把半径为1的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图所示的恒星图形,那么这个恒星图形的面积等于______.
7.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为______.
8.如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N,分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为______.
C组(综合题)
9.如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径,则阴影部分的面积______.
专题三 圆与相似
1.如图,在四边形ABCD中,AB∥DC,∠B=∠D.过点C作CH⊥AB交DA的延长线于点E,设垂足为H.以CE为直径作⊙O分别交AD,BC于点F,G,连接CF,若CF=CH.
(1)求证:四边形ABCD为菱形;
(2)若tanB=,OH=9,求AE的长.
2.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连接CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
4.如图,已知在Rt△ABC中,∠ACB=90°,AC=4,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A,P是上的一个动点.
(1)求半径OB的长;
(2)如果点P是的中点,连接PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP,CA交于点D,求线段DP的长.
5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=,求DG的长.
参考答案
2020-2021学年北师大版九年级数学下册第三章 圆 章末专题复习练习题
专题一 与圆周角有关的计算
A组(基础题)
1.如图,AB是⊙O的直径,点C,D是圆上两点,且∠AOC=126°,则∠CDB=(C)
A.54° B.64° C.27° D.37°
2.(2020·绍兴)如图,点A,B,C,D,E均在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD的度数为(D)
A.45° B.60° C.75° D.90°
3.如图,已知⊙O的半径为5,弦AB,CD所对的圆心角分别是∠AOB,∠COD.若∠AOB与∠COD互补,弦CD=6,则弦AB的长为(B)
A.6 B.8 C.5 D.5
4.如图,在半径为3的⊙O中,AB是直径,AC是弦,D是的中点,AC与BD相交于点E.若E是BD的中点,则AC的长是(D)
A. B.3 C.3 D.4
5.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB=70°.
6.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC.若AB=8,CD=2,则EC的长为2.
7.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的平分线交⊙O于点D.若AC=6,BD=5,则BC的长为8.
B组(中档题)
8.如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA,CB分别交半圆于点D,E.若△CDE的面积与四边形ABED的面积相等,则∠C等于45°.
9.如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC交AC的延长线于点E,连接OE交AD于点F.若cos∠BAC=,AF=8,则DF的长为5.
C组(综合题)
10.如图,△ABC内接于⊙O,AH⊥BC于点H.若AC=24,AH=18,⊙O的半径OC=13,则AB=.
专题二 与圆有关阴影部分面积的计算
A组(基础题)
1.如图,在?ABCD中,∠B=60°,⊙C的半径为3,则图中阴影部分的面积是(C)
A.π B.2π C.3π D.6π
2.如图,△ABC内接于⊙O,若∠A=45°,⊙O的半径r=4,则阴影部分的面积为(A)
A.4π-8 B.2π C.4π D.8π-8
3.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,连接OC,DB.如果OC∥DB,OC=2,那么图中阴影部分的面积是(B)
A.π B.2π C.3π D.4π
4.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为(A)
A.6π B.3π C.2π D.2π
5.如图,在Rt△ABC中,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE,OF,则图中阴影部分的面积是-π.
B组(中档题)
6.把半径为1的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图所示的恒星图形,那么这个恒星图形的面积等于4-π.
7.如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在上,则图中阴影部分的面积为-.
8.如图,正方形ABCD边长为2,E是AB的中点,以E为圆心,线段ED的长为半径作半圆,交直线AB于点M,N,分别以线段MD,ND为直径作半圆,则图中阴影部分的面积为2.
C组(综合题)
9.如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径,则阴影部分的面积16-4-π.
专题三 圆与相似
1.如图,在四边形ABCD中,AB∥DC,∠B=∠D.过点C作CH⊥AB交DA的延长线于点E,设垂足为H.以CE为直径作⊙O分别交AD,BC于点F,G,连接CF,若CF=CH.
(1)求证:四边形ABCD为菱形;
(2)若tanB=,OH=9,求AE的长.
解:(1)证明:∵AB∥CD,
∴∠D+∠DAB=180°.
∵∠B=∠D,
∴∠B+∠DAB=180°.
∴AD∥BC.
∴四边形ABCD是平行四边形.
∵CE是⊙O的直径,CH⊥AB,
∴∠CFD=90°=∠CHB.
∵CF=CH,∴△CFD≌△CHB(AAS).
∴CD=CB.∴四边形ABCD是菱形.
(2)由(1)可知,BC∥AD,CF⊥AD,
∴BC⊥CF.∴∠B=∠BAE.
∵BH=DF,AB=AD,∴AF=AH.
∵tan∠B==tan∠BAE,
∴设AH=4a,则HE=3a,AE=5a,AF=4a,EF=9a.
∵∠E=∠E,∠AHE=∠EFC=90°,
∴△EAH∽△ECF.
∴=.
∴=.
∴CE=15a.
∵OH=9,∴15a=2(3a+9).
∴a=2.
∴AE=5a=10.
2.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=5.C是直线l上一点,连接CP并延长交⊙O于另一点B,且AB=AC.
(1)求证:AB是⊙O的切线;
(2)若⊙O的半径为3,求线段BP的长.
解:(1)证明:连接OB,则OP=OB,
∴∠OBP=∠OPB=∠CPA.
∵AB=AC,
∴∠ACB=∠ABC.
∵OA⊥l,∴∠OAC=90°.
∴∠ACB+∠CPA=90°.
∴∠ABP+∠OBP=90°,
即∠ABO=90°.
∴OB⊥AB.
又∵OB是⊙O的半径,
∴AB是⊙O的切线.
(2)由(1)知,∠ABO=90°,
∵OA=5,OB=3,
∴由勾股定理,得AB=4.
过点O作OD⊥PB于点D,则PD=DB,
∵∠OPD=∠CPA,∠ODP=∠CAP=90°,
∴△ODP∽△CAP.
∴=.
又∵AC=AB=4,AP=OA-OP=2,
∴PC==2.
∴PD==.
∴BP=2PD=.
3.如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6,=,求BE的长.
解:(1)证明:连接OD,∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∴∠ADO+∠CDA=90°,即∠CDO=90°.
∴OD⊥CD.
又∵OD是⊙O的半径,∴CD是⊙O的切线.
(2)∵∠C=∠C,∠CDA=∠CBD,
∴△CDA∽△CBD.∴=.
∵=,BC=6,∴CD=4.
∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC.
∴BE2+BC2=EC2,即BE2+62=(4+BE)2.
解得BE=.
4.如图,已知在Rt△ABC中,∠ACB=90°,AC=4,BC=16.点O在边BC上,以O为圆心,OB为半径的弧经过点A,P是上的一个动点.
(1)求半径OB的长;
(2)如果点P是的中点,连接PC,求∠PCB的正切值;
(3)如果BA平分∠PBC,延长BP,CA交于点D,求线段DP的长.
解:(1)∵Rt△ABC中,∠ACB=90°,AC=4,BC=16,
∴AB==12.
过点O作OH⊥AB于点H,
则BH=AB=6.
∵∠BHO=∠ACB=90°,∠B=∠B,
∴△BHO∽△BCA.∴=.
∴=.∴OB=9.
(2)如图1,连接OP交AB于点H,过点P作PE⊥BC于点E,
∵点P是的中点,
∴OP⊥AB,AH=BH=AB=6.
在Rt△BHO中,OH==3.
在△POE和△BOH中,
∴△POE≌△BOH(AAS).
∴PE=HB=6,OE=OH=3.
∴CE=BC-OB+OE=10.
∴tan∠PCB==.
(3)如图2,过点A作AE⊥BD于点E,连接CP,
∵BA平分∠PBC,AC⊥BC,
∴AE=AC=4.
∵∠AED=∠ACB=90°,∠D=∠D,
∴△ADE∽△BDC.∴=.
设DE=x,∴=.∴CD=2.
在Rt△ACB和Rt△AEB中,
∴Rt△ACB≌Rt△AEB(HL).
∴BE=BC=16.
∵CD2+BC2=BD2,
∴(2)2+162=(16+x)2,解得x=.
∴BD=16+=.
∴过点O作OF⊥PB交PB于点F,
则△OBF∽△DBC,∴=.
∴=.∴BF=7.∴PB=2BF=14.
∴PD=BD-BP=.
5.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=,求DG的长.
解:(1)证明:连接OD,
∵AD为∠BAC的角平分线,∴∠BAD=∠CAD.
∵OA=OD,
∴∠ODA=∠OAD.
∴∠ODA=∠CAD.
∴OD∥AC.
∵∠C=90°,∴∠ODC=90°.
∴OD⊥BC.
∵OD是⊙O的半径,∴BC是⊙O的切线.
(2)连接DF,由(1)知BC为⊙O的切线,
∴∠FDC=∠DAF.∴∠CDA=∠CFD.
∵∠BAD=∠DAF.∴△ABD∽△ADF.
∴=,即AD2=AB·AF=xy,
∴AD=.
(3)连接EF,在Rt△BOD中,sinB==,
设圆的半径为r,可得=,
解得r=5.∴AE=10,AB=18.
∵AE是直径,∴∠AFE=∠C=90°.
∴EF∥BC,∴∠AEF=∠B.
∴sin∠AEF==.
∴AF=AE·sin∠AEF=10×=.
∵AF∥OD,
∴===,即DG=AD.
由(2)知AD===,
则DG=×=.
