24、2与圆有关的位置关系复习
文档属性
| 名称 | 24、2与圆有关的位置关系复习 |

|
|
| 格式 | zip | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-04 00:00:00 | ||
图片预览


文档简介
24、2与圆有关的位置关系复习
教学目标
1、掌握点与圆的位置关系、直线与圆的位置关系以及圆与圆的位置关系的相关内容
2、要求学生学会用动态的观点理解和解决与圆有关的位置关系的问题。
教学重难点
圆中的位置关系及应用
教学过程
一、知识点回顾:
1.点与圆的位置关系
A点在圆 OA r B点在圆 OB r
C点在圆 OC r
确定圆的条件
不在同一直线上的三个点确定一个圆.
三角形的外接圆
(1)定义:经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆.
三角形的外心:外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心,这个三角形叫做这个圆的内接三角形.
注意:①要弄清“接”是指三角形各顶点在圆上,“外”是指三角形外,“内”是指圆内.
②三角形的外接圆和圆的内接三角形是针对上述同一个图形,从不同角度的两种说法.
(2)三角形外心的性质:
①三角形的外心是外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等.
②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是惟一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.
例题:1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有( )
A.1 B.2 C.3 D.4
2.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙O的位置关系是( )
A.点D在⊙A外 B.点D在⊙A上 C.点D在⊙A内 D.无法确定
( http: / / )
(第2题图) (第3题图)
3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,则弦AD长为( )
A. B. C. D.3
练习:
1.经过一点P可以作_______个圆;经过两点P、Q可以作________个圆,圆心在_________上;经过不在同一直线上的三个点可以作________个圆,圆心是________ 的交点.
2.在平面内,⊙O的半径为5cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .
3.直角三角形的外心是______ 的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.
4、△ABC中,点O是它的外心,BC=24㎝,点O到BC的距离是5㎝,则△ABC外接圆的半径________.
2. 直线与圆的位置关系(设⊙O半径为,圆心到直线距离为)
①与⊙O相交 r ②与⊙O相切 r ③与⊙O相离 r
切线
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)切线的性质:圆的切线垂直于过切点的半径.
(3)切线长:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
(4)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
三角形的内切圆与三角形的内心
①与三角形各边都相切的圆叫做三角形的内切圆.三角形内切圆的圆心叫做三角形的内心.这个三角形叫做圆的外切三角形.
②三角形的内心就是三角形三条内角平分线的交点,三角形的内心到三边的距离相等.
例题:
1.Rt△ABC中,∠C=90°,∠AC=3cm,BC=4cm,给出下列三个结论:
①以点C为圆心2.3 cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交.上述结论中正确的个数是( )
A.0个 B.l个 C.2个 D.3个
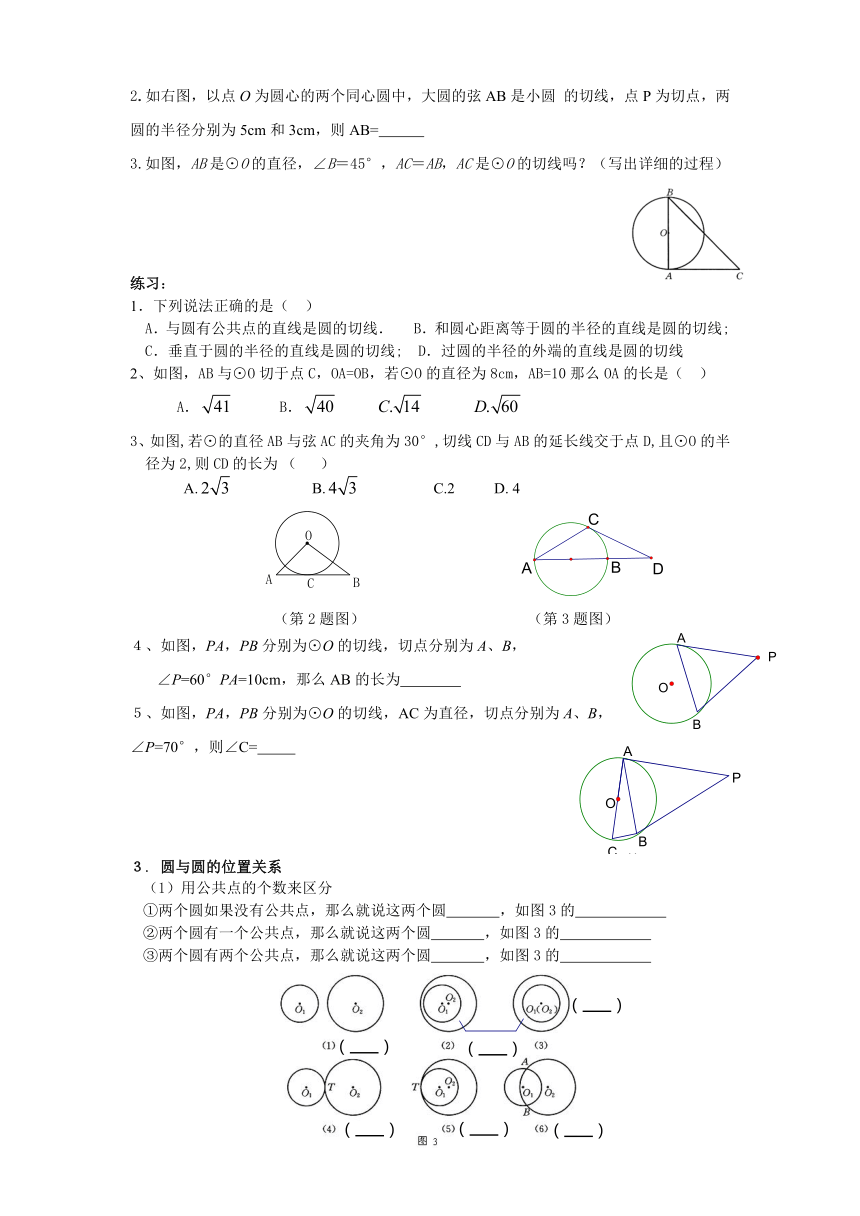
2.如右图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆 的切线,点P为切点,两圆的半径分别为5cm和3cm,则AB=
3.如图,AB是⊙O的直径,∠B=45°,AC=AB,AC是⊙O的切线吗?(写出详细的过程)
练习:
1.下列说法正确的是( )
A.与圆有公共点的直线是圆的切线. B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线; D.过圆的半径的外端的直线是圆的切线
2、如图,AB与⊙O切于点C,OA=OB,若⊙O的直径为8cm,AB=10那么OA的长是( )
A. B.
3、如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 ( )
A. B. C.2 D. 4
(第2题图) (第3题图)
4、如图,PA,PB分别为⊙O的切线,切点分别为A、B,
∠P=60°PA=10cm,那么AB的长为
5、如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C=
3. 圆与圆的位置关系
(1)用公共点的个数来区分
①两个圆如果没有公共点,那么就说这两个圆 ,如图3的
②两个圆有一个公共点,那么就说这两个圆 ,如图3的
③两个圆有两个公共点,那么就说这两个圆 ,如图3的
(2)用数量关系来区别:设两圆的半径分别为、,圆心距为:
两圆的位置关系 数量关系
外 离
外 切
相 交
内 切
内 含
例题:
1、 如图所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
2、已知⊙O1的半径为6厘米,⊙O2的半径为8厘米,圆心距为 d,
则:R+r= , R-r= ;
(1)当d=14厘米时,因为d R+r,则⊙O1和⊙O2位置关系是:
(2)当d=2厘米时, 因为d R-r,则⊙O1和⊙O2位置关系是:
(3)当d=15厘米时,因为 ,则⊙O1和⊙O2位置关系是:
(4)当d=7厘米时, 因为 ,则⊙O1和⊙O2位置关系是:
(5)当d=1厘米时, 因为 ,则⊙O1和⊙O2位置关系是:
3.如图,直线AB、CD相交于点O,∠AOC=300,半径为
1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果
⊙P以1cm/秒的速度沿由A向B的方向移动,那么当
⊙P的运动时间t(秒)满足条件 时,
⊙P与直线CD相交.
如图,在△ABC中,∠C = 90°,BC =3,AC =4,求它的内切圆半径是。
练习:
1.已知两圆的半径分别为5cm和7cm,圆心距为8cm,那么这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2 、已知 ⊙ A 与⊙ B 相切,两圆的圆心距为 8㎝, ⊙ A 的半径为 3㎝,则 ⊙ B 的半径( )
A 、5㎝ B、 11 ㎝ C、3㎝ D、5㎝或 11 ㎝
3 、如图所示,两个等圆 ⊙ O 和 ⊙ O 1 相切,过 O 作 ⊙ O 1 的两条切线 OA 、 OB,A 、B为切点,则∠ AOB= __________
4、仔细观察如图所示的卡通脸谱,图中没有出现的两圆的位置关系是______.
5、如图,圆与圆之间不同的位置关系有( )
A.2种 B.3种 C.4种 D.5种
6、如图,已知线段AB=8cm,⊙P与⊙Q的半径均为1cm.点P、Q分别从A、B出发,在线段AB上按箭头所示方向运动.当P、Q两点未相遇前,在下列选项中,⊙P与⊙Q不可能出现的位置关系是( )
A.外离 B.外切 C.相交 D.内含
第3题图 第 4 题图
二、基础达标练习:
选择题:
1、已知⊙O的半径为6,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
A.在圆上 B.在圆外 C.在圆内 D.不确定
2、圆最长弦为12,如果直线与圆相交,且直线与圆心的距离为,那么( )
A. B. C. D.
3、已知圆⊙O1和⊙O2的半径的6cm和8cm,当O1O2=12cm时, ⊙O1和⊙O2的位置关系为( )
A.外切 B.相交 C. 内切 D.内含
4、两圆半径和为24cm,半径之比为1:2,圆心距为8cm,则两圆的位置关系为( )
A.外离 B.相交 C. 内切 D.外切
5.两个同心圆的半径分别为1cm和2cm,大圆的弦AB与小圆相切,那么AB=( )
A. B.2 C.3 D.4
6.已知两圆的半径分别为3 cm和4 cm,圆心距为1cm,那么两圆的位置关系是( )
A.相离 B.相交 C.内切 D.外切
7.两圆既不相交又不相切,半径分别为3和5,则两圆的圆心距d的取值范围是( )
A.d>8 B.0<d≤2
C.2<d<8 D.0≤d<2或d>8
填空题:
8.在△ABC中,∠C=90°,AC=3cm,BC=4cm,CM是中线,以C为圆心,以3cm长为半径画圆,则对A、B、C、M四点,在圆外的有______,在圆上的有________,在圆内的有________.
9.△ABC中,∠C=90°,AC=3,CB=4,若以C为圆心,以r为半径作圆,那么:
⑴ 当直线AB与⊙C相离时,r的取值范围是____;
⑵ 当直线AB与⊙C相切时,r的取值范围是____;
⑶ 当直线AB与⊙C相交时,r的取值范围是____.
10.已知半径为3 cm,4cm的两圆外切,那么半径为6 cm且与这两圆都外切的圆共有___个.
11.已知⊙O1和⊙O2相外切,且圆心距为10cm,若⊙O1的半径为3cm,则⊙O2的半径为___cm.
12.已知两圆的圆心距是5,两圆的半径是方程的两实根,则两圆的位置关系是 。
解答题:
13、是⊙O的直径,切⊙O于,交⊙O于,连.若,求的度数.
14.如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,求AB的长.
15.如图,PA切⊙O于A,PB切⊙O于B, ∠APB=90°,OP=4,求⊙O的半径.
16. 已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
17、如图,是⊙O的直径,是弦,,延长到点,使得.
(1)求证:是⊙O的切线;
(2)若,求的长.
( http: / / www. )
18、已知图中各圆两两相切,⊙O的半径为2R,⊙O1、⊙O2的半径为R,求⊙O3的半径.
第5题图
P
第6题图
Q
A
B
A
B
C
P
O
教学目标
1、掌握点与圆的位置关系、直线与圆的位置关系以及圆与圆的位置关系的相关内容
2、要求学生学会用动态的观点理解和解决与圆有关的位置关系的问题。
教学重难点
圆中的位置关系及应用
教学过程
一、知识点回顾:
1.点与圆的位置关系
A点在圆 OA r B点在圆 OB r
C点在圆 OC r
确定圆的条件
不在同一直线上的三个点确定一个圆.
三角形的外接圆
(1)定义:经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆.
三角形的外心:外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心,这个三角形叫做这个圆的内接三角形.
注意:①要弄清“接”是指三角形各顶点在圆上,“外”是指三角形外,“内”是指圆内.
②三角形的外接圆和圆的内接三角形是针对上述同一个图形,从不同角度的两种说法.
(2)三角形外心的性质:
①三角形的外心是外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等.
②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是惟一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.
例题:1.下列说法:①三点确定一个圆;②三角形有且只有一个外接圆;③圆有且只有一个内接三角形;④三角形的外心是各边垂直平分线的交点;⑤三角形的外心到三角形三边的距离相等;⑥等腰三角形的外心一定在这个三角形内,其中正确的个数有( )
A.1 B.2 C.3 D.4
2.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙O的位置关系是( )
A.点D在⊙A外 B.点D在⊙A上 C.点D在⊙A内 D.无法确定
( http: / / )
(第2题图) (第3题图)
3.如图,△ABC内接于⊙O,AB是直径,BC=4,AC=3,CD平分∠ACB,则弦AD长为( )
A. B. C. D.3
练习:
1.经过一点P可以作_______个圆;经过两点P、Q可以作________个圆,圆心在_________上;经过不在同一直线上的三个点可以作________个圆,圆心是________ 的交点.
2.在平面内,⊙O的半径为5cm,点P到圆心O的距离为3cm,则点P与⊙O的位置关系是 .
3.直角三角形的外心是______ 的中点,锐角三角形外心在三角形______,钝角三角形外心在三角形_________.
4、△ABC中,点O是它的外心,BC=24㎝,点O到BC的距离是5㎝,则△ABC外接圆的半径________.
2. 直线与圆的位置关系(设⊙O半径为,圆心到直线距离为)
①与⊙O相交 r ②与⊙O相切 r ③与⊙O相离 r
切线
(1)切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
(2)切线的性质:圆的切线垂直于过切点的半径.
(3)切线长:圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
(4)切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
三角形的内切圆与三角形的内心
①与三角形各边都相切的圆叫做三角形的内切圆.三角形内切圆的圆心叫做三角形的内心.这个三角形叫做圆的外切三角形.
②三角形的内心就是三角形三条内角平分线的交点,三角形的内心到三边的距离相等.
例题:
1.Rt△ABC中,∠C=90°,∠AC=3cm,BC=4cm,给出下列三个结论:
①以点C为圆心2.3 cm长为半径的圆与AB相离;②以点C为圆心,2.4cm长为半径的圆与AB相切;③以点C为圆心,2.5cm长为半径的圆与AB相交.上述结论中正确的个数是( )
A.0个 B.l个 C.2个 D.3个
2.如右图,以点O为圆心的两个同心圆中,大圆的弦AB是小圆 的切线,点P为切点,两圆的半径分别为5cm和3cm,则AB=
3.如图,AB是⊙O的直径,∠B=45°,AC=AB,AC是⊙O的切线吗?(写出详细的过程)
练习:
1.下列说法正确的是( )
A.与圆有公共点的直线是圆的切线. B.和圆心距离等于圆的半径的直线是圆的切线;
C.垂直于圆的半径的直线是圆的切线; D.过圆的半径的外端的直线是圆的切线
2、如图,AB与⊙O切于点C,OA=OB,若⊙O的直径为8cm,AB=10那么OA的长是( )
A. B.
3、如图,若⊙的直径AB与弦AC的夹角为30°,切线CD与AB的延长线交于点D,且⊙O的半径为2,则CD的长为 ( )
A. B. C.2 D. 4
(第2题图) (第3题图)
4、如图,PA,PB分别为⊙O的切线,切点分别为A、B,
∠P=60°PA=10cm,那么AB的长为
5、如图,PA,PB分别为⊙O的切线,AC为直径,切点分别为A、B,∠P=70°,则∠C=
3. 圆与圆的位置关系
(1)用公共点的个数来区分
①两个圆如果没有公共点,那么就说这两个圆 ,如图3的
②两个圆有一个公共点,那么就说这两个圆 ,如图3的
③两个圆有两个公共点,那么就说这两个圆 ,如图3的
(2)用数量关系来区别:设两圆的半径分别为、,圆心距为:
两圆的位置关系 数量关系
外 离
外 切
相 交
内 切
内 含
例题:
1、 如图所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
2、已知⊙O1的半径为6厘米,⊙O2的半径为8厘米,圆心距为 d,
则:R+r= , R-r= ;
(1)当d=14厘米时,因为d R+r,则⊙O1和⊙O2位置关系是:
(2)当d=2厘米时, 因为d R-r,则⊙O1和⊙O2位置关系是:
(3)当d=15厘米时,因为 ,则⊙O1和⊙O2位置关系是:
(4)当d=7厘米时, 因为 ,则⊙O1和⊙O2位置关系是:
(5)当d=1厘米时, 因为 ,则⊙O1和⊙O2位置关系是:
3.如图,直线AB、CD相交于点O,∠AOC=300,半径为
1cm的⊙P的圆心在射线OA上,开始时,PO=6cm.如果
⊙P以1cm/秒的速度沿由A向B的方向移动,那么当
⊙P的运动时间t(秒)满足条件 时,
⊙P与直线CD相交.
如图,在△ABC中,∠C = 90°,BC =3,AC =4,求它的内切圆半径是。
练习:
1.已知两圆的半径分别为5cm和7cm,圆心距为8cm,那么这两个圆的位置关系是( )
A.内切 B.相交 C.外切 D.外离
2 、已知 ⊙ A 与⊙ B 相切,两圆的圆心距为 8㎝, ⊙ A 的半径为 3㎝,则 ⊙ B 的半径( )
A 、5㎝ B、 11 ㎝ C、3㎝ D、5㎝或 11 ㎝
3 、如图所示,两个等圆 ⊙ O 和 ⊙ O 1 相切,过 O 作 ⊙ O 1 的两条切线 OA 、 OB,A 、B为切点,则∠ AOB= __________
4、仔细观察如图所示的卡通脸谱,图中没有出现的两圆的位置关系是______.
5、如图,圆与圆之间不同的位置关系有( )
A.2种 B.3种 C.4种 D.5种
6、如图,已知线段AB=8cm,⊙P与⊙Q的半径均为1cm.点P、Q分别从A、B出发,在线段AB上按箭头所示方向运动.当P、Q两点未相遇前,在下列选项中,⊙P与⊙Q不可能出现的位置关系是( )
A.外离 B.外切 C.相交 D.内含
第3题图 第 4 题图
二、基础达标练习:
选择题:
1、已知⊙O的半径为6,A为线段PO的中点,当OP=10时,点A与⊙O的位置关系为( )
A.在圆上 B.在圆外 C.在圆内 D.不确定
2、圆最长弦为12,如果直线与圆相交,且直线与圆心的距离为,那么( )
A. B. C. D.
3、已知圆⊙O1和⊙O2的半径的6cm和8cm,当O1O2=12cm时, ⊙O1和⊙O2的位置关系为( )
A.外切 B.相交 C. 内切 D.内含
4、两圆半径和为24cm,半径之比为1:2,圆心距为8cm,则两圆的位置关系为( )
A.外离 B.相交 C. 内切 D.外切
5.两个同心圆的半径分别为1cm和2cm,大圆的弦AB与小圆相切,那么AB=( )
A. B.2 C.3 D.4
6.已知两圆的半径分别为3 cm和4 cm,圆心距为1cm,那么两圆的位置关系是( )
A.相离 B.相交 C.内切 D.外切
7.两圆既不相交又不相切,半径分别为3和5,则两圆的圆心距d的取值范围是( )
A.d>8 B.0<d≤2
C.2<d<8 D.0≤d<2或d>8
填空题:
8.在△ABC中,∠C=90°,AC=3cm,BC=4cm,CM是中线,以C为圆心,以3cm长为半径画圆,则对A、B、C、M四点,在圆外的有______,在圆上的有________,在圆内的有________.
9.△ABC中,∠C=90°,AC=3,CB=4,若以C为圆心,以r为半径作圆,那么:
⑴ 当直线AB与⊙C相离时,r的取值范围是____;
⑵ 当直线AB与⊙C相切时,r的取值范围是____;
⑶ 当直线AB与⊙C相交时,r的取值范围是____.
10.已知半径为3 cm,4cm的两圆外切,那么半径为6 cm且与这两圆都外切的圆共有___个.
11.已知⊙O1和⊙O2相外切,且圆心距为10cm,若⊙O1的半径为3cm,则⊙O2的半径为___cm.
12.已知两圆的圆心距是5,两圆的半径是方程的两实根,则两圆的位置关系是 。
解答题:
13、是⊙O的直径,切⊙O于,交⊙O于,连.若,求的度数.
14.如图,已知两同心圆,大圆的弦AB切小圆于M,若环形的面积为9π,求AB的长.
15.如图,PA切⊙O于A,PB切⊙O于B, ∠APB=90°,OP=4,求⊙O的半径.
16. 已知:如图,AB是⊙O的直径,BC是和⊙O相切于点B的切线,⊙O的弦AD平行于OC.求证:DC是⊙O的切线.
17、如图,是⊙O的直径,是弦,,延长到点,使得.
(1)求证:是⊙O的切线;
(2)若,求的长.
( http: / / www. )
18、已知图中各圆两两相切,⊙O的半径为2R,⊙O1、⊙O2的半径为R,求⊙O3的半径.
第5题图
P
第6题图
Q
A
B
A
B
C
P
O
同课章节目录
