24、1圆的概念和性质复习
文档属性
| 名称 | 24、1圆的概念和性质复习 | 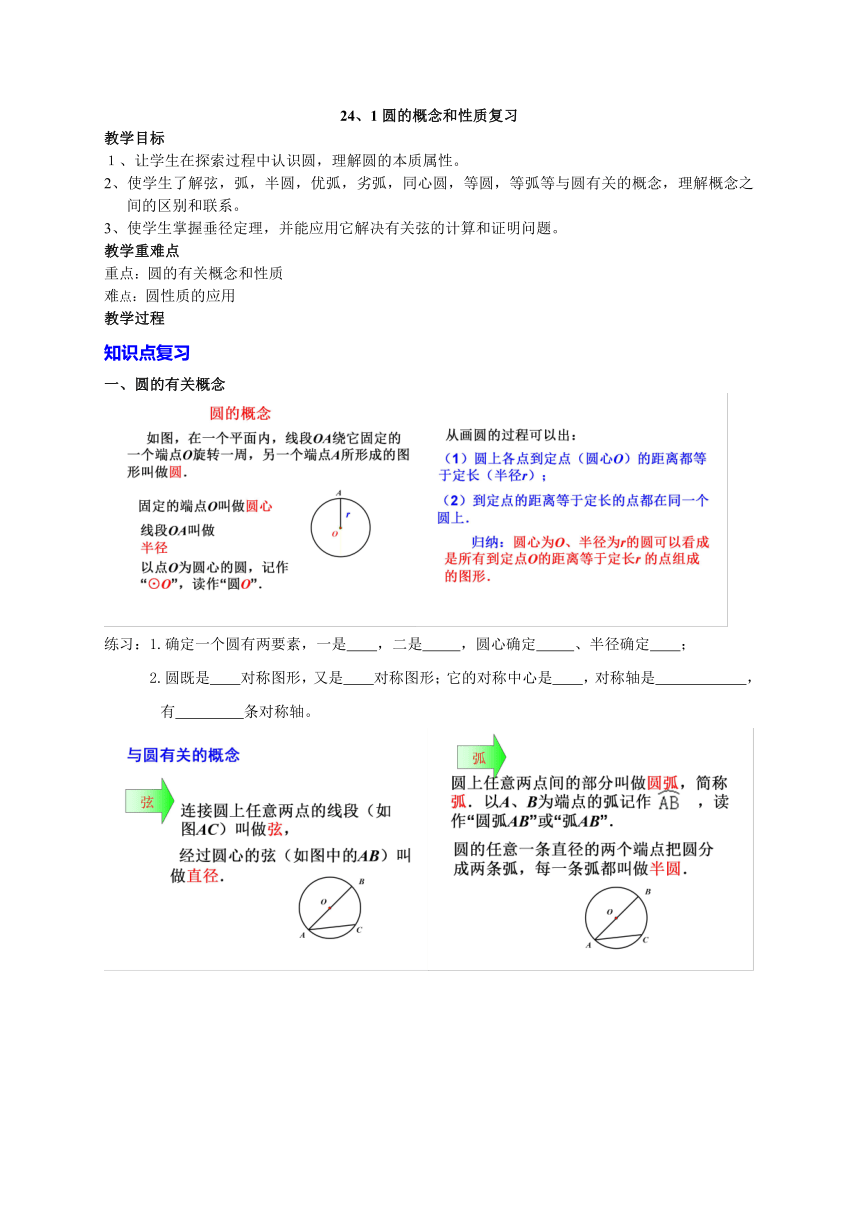 | |
| 格式 | zip | ||
| 文件大小 | 254.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-04 15:29:26 | ||
图片预览


文档简介
24、1圆的概念和性质复习
教学目标
1、让学生在探索过程中认识圆,理解圆的本质属性。
2、使学生了解弦,弧,半圆,优弧,劣弧,同心圆,等圆,等弧等与圆有关的概念,理解概念之间的区别和联系。
3、使学生掌握垂径定理,并能应用它解决有关弦的计算和证明问题。
教学重难点
重点:圆的有关概念和性质
难点:圆性质的应用
教学过程
知识点复习
一、圆的有关概念
练习:1.确定一个圆有两要素,一是 ,二是 ,圆心确定 、半径确定 ;
2.圆既是 对称图形,又是 对称图形;它的对称中心是 ,对称轴是 ,
有 条对称轴。
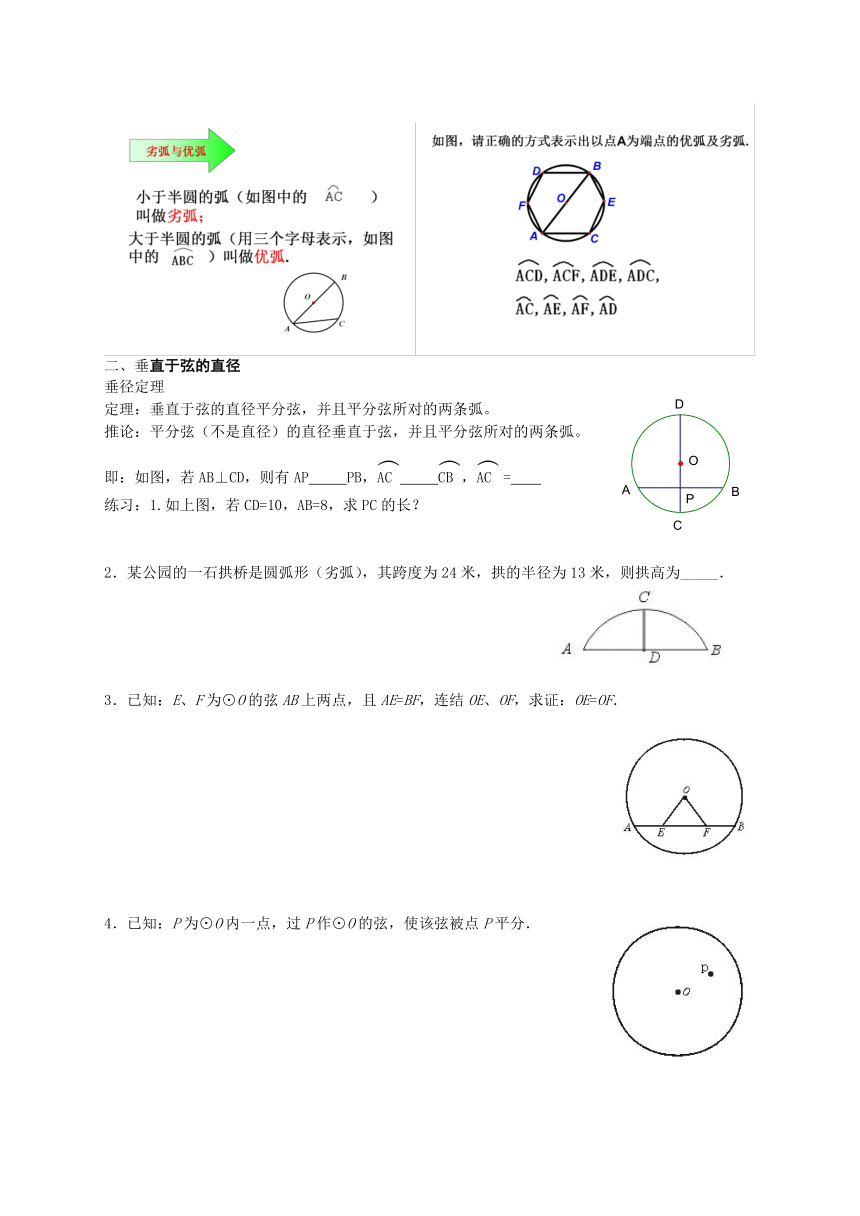
二、垂直于弦的直径
垂径定理
定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
即:如图,若AB⊥CD,则有AP PB, , =
练习:1.如上图,若CD=10,AB=8,求PC的长?
2.某公园的一石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为_____.
3.已知:E、F为⊙O的弦AB上两点,且AE=BF,连结OE、OF,求证:OE=OF.
4.已知:P为⊙O内一点,过P作⊙O的弦,使该弦被点P平分.
三、弧、弦、圆心角
1、顶点在圆心的角叫做圆心角.
2、在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一对量相等,那么它们所对应的其余各对量都相等.
3.在同圆或等圆中,证明线段相等往往可以转化为证明角或弧相等,证明角相等往往可以转化为证明弧或弦相等.
练习:
1:如图,AB、CD是⊙O的两条弦
① 若AB=CD, 则有 = , =
② 若AB=CD, 则有 = , =
③ 若∠AOB=∠COD, 则有 = , =
2、如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且OD //AC.求证:
3.如图,∠AOB=90°,C、D是AB三等分点,AB分别交OC、OD于点E、F,
求证:AE=BF=CD.
4.如图,⊙O的直径AB为10cm,弦AC为6cm,,∠ACB的平分线交⊙O于D,求BC、AD、BD的长。
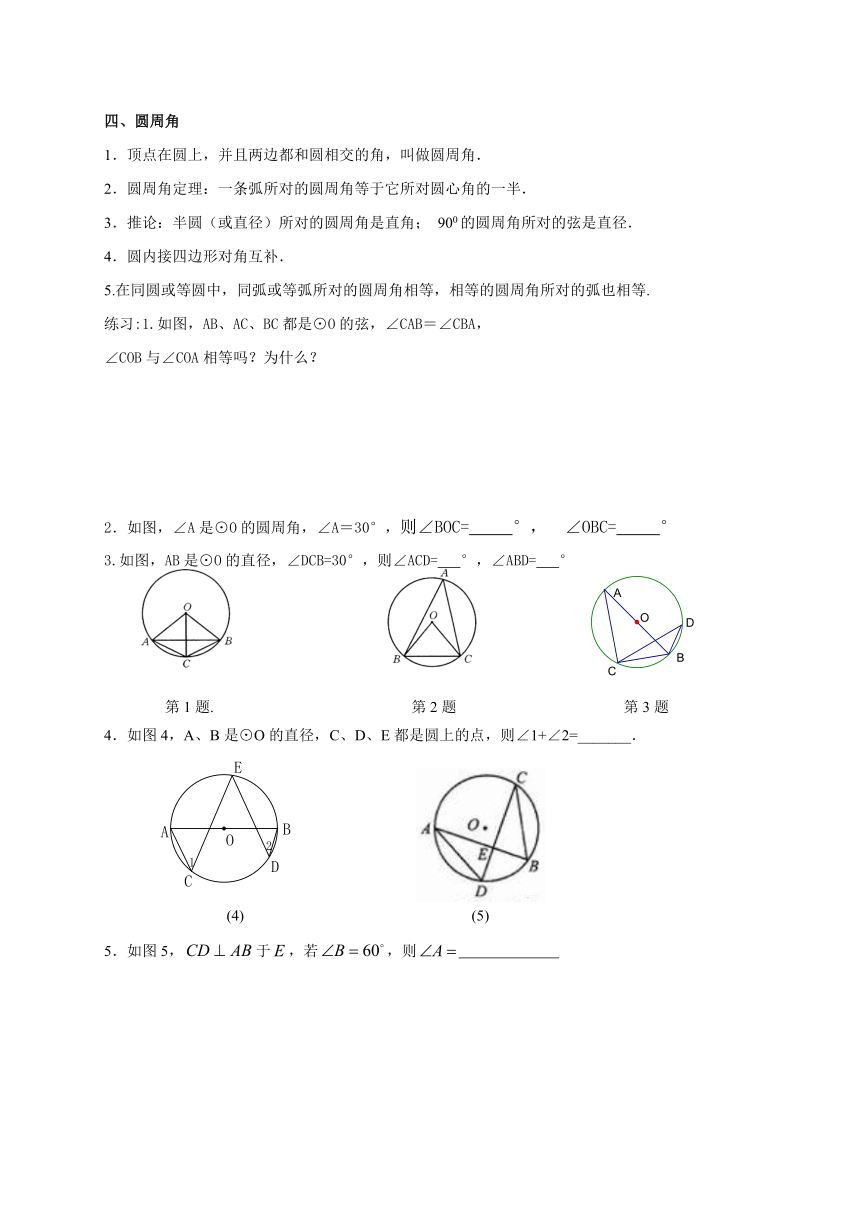
四、圆周角
1.顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
3.推论:半圆(或直径)所对的圆周角是直角; 900的圆周角所对的弦是直径.
4.圆内接四边形对角互补.
5.在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
练习:1.如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,
∠COB与∠COA相等吗?为什么?
2.如图,∠A是⊙O的圆周角,∠A=30°,则∠BOC= °, ∠OBC= °
3.如图,AB是⊙O的直径,∠DCB=30°,则∠ACD= °,∠ABD= °
第1题. 第2题 第3题
4.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.
(4) (5)
5.如图5,于,若,则
典型例题:
1.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).
A.140° B.110° C.120° D.130°
2.如图2, AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.130°
(1) (2)
3.下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④⑤
4.如图3,AB是⊙O的弦,OC是⊙O的半径,OC⊥AB于点D,AB=16cm,OD=6cm,那么⊙O的半径是__________cm.
5.如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交于D.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
课后练习:
1.如图,是⊙O的直径,,则的度数是( )
A. B. C. D.
2.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
3.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
4.如图,是⊙O的直径,为弦,于,则下列结论中不成立的是( )
A. B. C. D.
5.如图,为⊙O的直径,点在⊙O上,,则 .
6.已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=450。给出以下五个结论:①∠EBC=22.50,;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC。其中正确结论的序号是 .
7.如图,已知⊙O半径为5,弦长为8,点为弦上一动点,连结,则线段的最小长度是 .
8.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AD=6,则BC= 。
9.如图,已知AB是⊙O的弦,P是AB上一点,若AB=10,PB=4,OP=5,求⊙O的半径的长。
10.已知:如图等边内接于⊙O,点是劣弧上的一点(端点除外),延长至,使,连结.
(1)若过圆心,如图①,请你判断是什么三角形?并说明理由.
(2)若不过圆心,如图②,又是什么三角形?为什么?
O
D
B
A
C
C
B
A
O
A
O
E
C
B
A
D
O
B
O
B
P
A
A
O
C
D
P
B
图①
A
D
P
B
图②
教学目标
1、让学生在探索过程中认识圆,理解圆的本质属性。
2、使学生了解弦,弧,半圆,优弧,劣弧,同心圆,等圆,等弧等与圆有关的概念,理解概念之间的区别和联系。
3、使学生掌握垂径定理,并能应用它解决有关弦的计算和证明问题。
教学重难点
重点:圆的有关概念和性质
难点:圆性质的应用
教学过程
知识点复习
一、圆的有关概念
练习:1.确定一个圆有两要素,一是 ,二是 ,圆心确定 、半径确定 ;
2.圆既是 对称图形,又是 对称图形;它的对称中心是 ,对称轴是 ,
有 条对称轴。
二、垂直于弦的直径
垂径定理
定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
即:如图,若AB⊥CD,则有AP PB, , =
练习:1.如上图,若CD=10,AB=8,求PC的长?
2.某公园的一石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为_____.
3.已知:E、F为⊙O的弦AB上两点,且AE=BF,连结OE、OF,求证:OE=OF.
4.已知:P为⊙O内一点,过P作⊙O的弦,使该弦被点P平分.
三、弧、弦、圆心角
1、顶点在圆心的角叫做圆心角.
2、在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一对量相等,那么它们所对应的其余各对量都相等.
3.在同圆或等圆中,证明线段相等往往可以转化为证明角或弧相等,证明角相等往往可以转化为证明弧或弦相等.
练习:
1:如图,AB、CD是⊙O的两条弦
① 若AB=CD, 则有 = , =
② 若AB=CD, 则有 = , =
③ 若∠AOB=∠COD, 则有 = , =
2、如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且OD //AC.求证:
3.如图,∠AOB=90°,C、D是AB三等分点,AB分别交OC、OD于点E、F,
求证:AE=BF=CD.
4.如图,⊙O的直径AB为10cm,弦AC为6cm,,∠ACB的平分线交⊙O于D,求BC、AD、BD的长。
四、圆周角
1.顶点在圆上,并且两边都和圆相交的角,叫做圆周角.
2.圆周角定理:一条弧所对的圆周角等于它所对圆心角的一半.
3.推论:半圆(或直径)所对的圆周角是直角; 900的圆周角所对的弦是直径.
4.圆内接四边形对角互补.
5.在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
练习:1.如图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,
∠COB与∠COA相等吗?为什么?
2.如图,∠A是⊙O的圆周角,∠A=30°,则∠BOC= °, ∠OBC= °
3.如图,AB是⊙O的直径,∠DCB=30°,则∠ACD= °,∠ABD= °
第1题. 第2题 第3题
4.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.
(4) (5)
5.如图5,于,若,则
典型例题:
1.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).
A.140° B.110° C.120° D.130°
2.如图2, AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.130°
(1) (2)
3.下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④⑤
4.如图3,AB是⊙O的弦,OC是⊙O的半径,OC⊥AB于点D,AB=16cm,OD=6cm,那么⊙O的半径是__________cm.
5.如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交于D.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
课后练习:
1.如图,是⊙O的直径,,则的度数是( )
A. B. C. D.
2.已知:如图,四边形ABCD是⊙O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是( )
A.45° B.60° C.75° D.90°
3.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( )
A.第①块 B.第②块 C.第③块 D.第④块
4.如图,是⊙O的直径,为弦,于,则下列结论中不成立的是( )
A. B. C. D.
5.如图,为⊙O的直径,点在⊙O上,,则 .
6.已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=450。给出以下五个结论:①∠EBC=22.50,;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC。其中正确结论的序号是 .
7.如图,已知⊙O半径为5,弦长为8,点为弦上一动点,连结,则线段的最小长度是 .
8.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AD=6,则BC= 。
9.如图,已知AB是⊙O的弦,P是AB上一点,若AB=10,PB=4,OP=5,求⊙O的半径的长。
10.已知:如图等边内接于⊙O,点是劣弧上的一点(端点除外),延长至,使,连结.
(1)若过圆心,如图①,请你判断是什么三角形?并说明理由.
(2)若不过圆心,如图②,又是什么三角形?为什么?
O
D
B
A
C
C
B
A
O
A
O
E
C
B
A
D
O
B
O
B
P
A
A
O
C
D
P
B
图①
A
D
P
B
图②
同课章节目录
