2020-2021学年七年级下册数学湘教新版《第4章 相交线与平行线》单元测试卷(word有答案)
文档属性
| 名称 | 2020-2021学年七年级下册数学湘教新版《第4章 相交线与平行线》单元测试卷(word有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 237.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 17:00:02 | ||
图片预览



文档简介
2020-2021学年七年级下册数学湘教新版《第4章
相交线与平行线》单元测试卷
一.选择题
1.任意画三条直线,交点的个数是( )
A.1
B.1或3
C.0或1或2或3
D.不能确定
2.如图所示,直线l1与l2,l3相交,构成的八个角中,已知∠1=∠8,则与∠8互补的角有( )
A.1个
B.2个
C.3个
D.4个
3.下列说法中正确的是( )
A.在同一平面内,两条不平行的线段必相交
B.在同一平面内,不相交的两条线段是平行线
C.两条射线或线段平行是指它们所在的直线平行
D.一条直线有可能同时与两条相交直线平行
4.如图所示,按各组角的位置判断错误的是( )
A.∠2和∠A是同旁内角
B.∠1和∠4是内错角
C.∠2和∠B是同旁内角
D.∠3和∠B是同位角
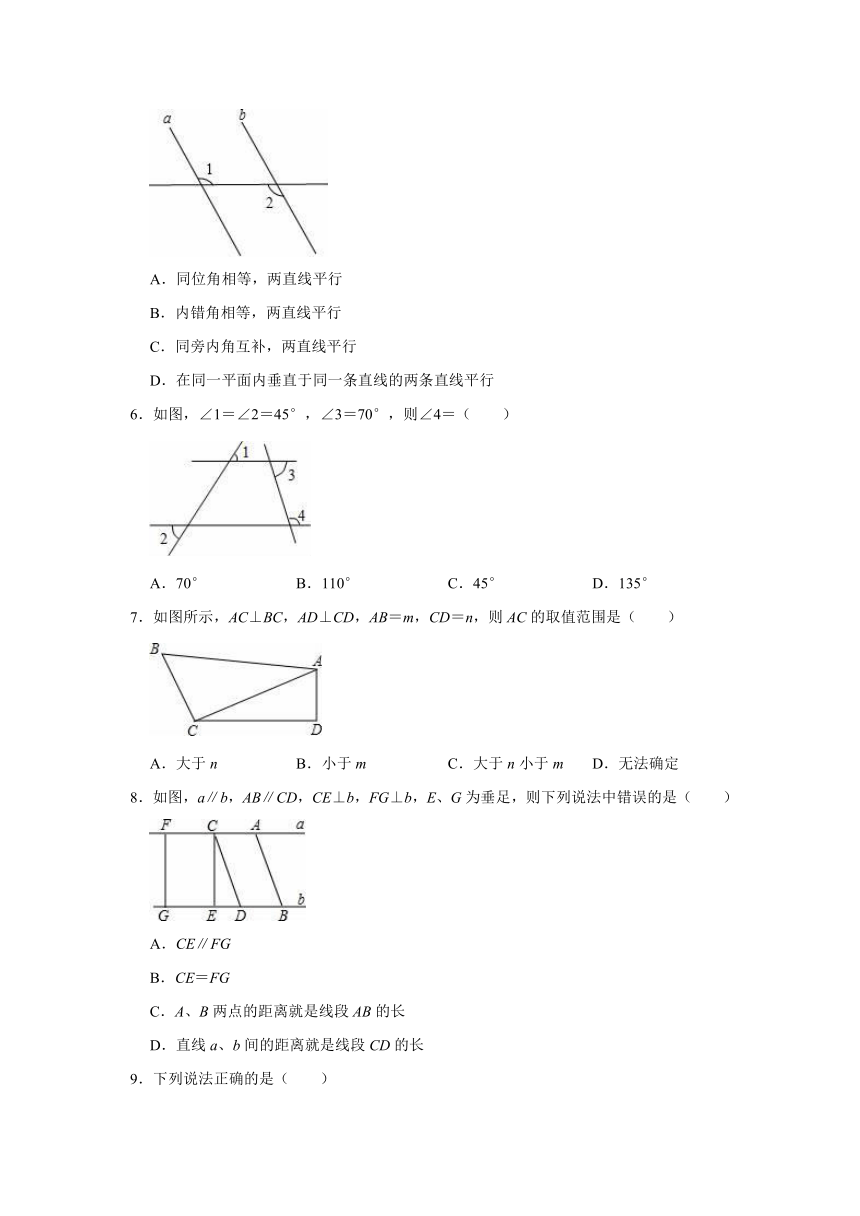
5.如图,由∠1=∠2,得出结论a∥b,其根据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.在同一平面内垂直于同一条直线的两条直线平行
6.如图,∠1=∠2=45°,∠3=70°,则∠4=( )
A.70°
B.110°
C.45°
D.135°
7.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n
B.小于m
C.大于n小于m
D.无法确定
8.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E、G为垂足,则下列说法中错误的是( )
A.CE∥FG
B.CE=FG
C.A、B两点的距离就是线段AB的长
D.直线a、b间的距离就是线段CD的长
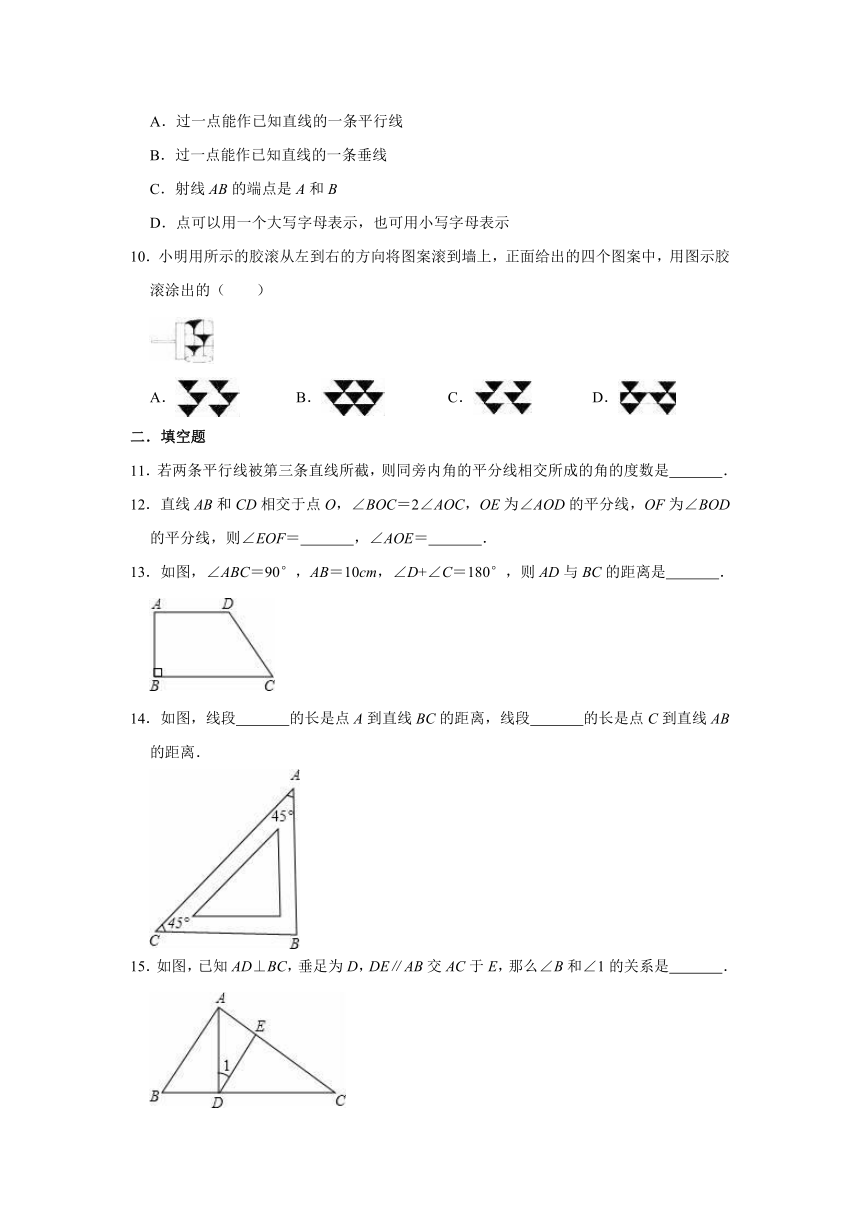
9.下列说法正确的是( )
A.过一点能作已知直线的一条平行线
B.过一点能作已知直线的一条垂线
C.射线AB的端点是A和B
D.点可以用一个大写字母表示,也可用小写字母表示
10.小明用所示的胶滚从左到右的方向将图案滚到墙上,正面给出的四个图案中,用图示胶滚涂出的( )
A.
B.
C.
D.
二.填空题
11.若两条平行线被第三条直线所截,则同旁内角的平分线相交所成的角的度数是
.
12.直线AB和CD相交于点O,∠BOC=2∠AOC,OE为∠AOD的平分线,OF为∠BOD的平分线,则∠EOF=
,∠AOE=
.
13.如图,∠ABC=90°,AB=10cm,∠D+∠C=180°,则AD与BC的距离是
.
14.如图,线段
的长是点A到直线BC的距离,线段
的长是点C到直线AB的距离.
15.如图,已知AD⊥BC,垂足为D,DE∥AB交AC于E,那么∠B和∠1的关系是
.
16.如图,将方格中的图案作下列变换,请画出相应的图案:沿y轴正向平移4个单位,并写出平移后圆心的坐标
.
17.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必
.
18.如图所示,△ABC是△DEF经过平移得到的,若AD=4cm,则BE=
cm,CF=
cm;若点M为AB的中点,点N为DE的中点,则MN=
cm;若∠B=73°,则∠E=
.
19.如图,∠1=56°,∠2=124°,∠3=85°,则∠4=
.
20.在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也
.
三.解答题
21.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
22.平面上有7条不同的直线,如果其中任何三条直线都不共点.
(1)请画出满足上述条件的一个图形,并数出图形中各直线之间的交点个数;
(2)请再画出各直线之间的交点个数不同的图形(至少两个);
(3)你能否画出各直线之间的交点个数为n的图形,其中n分别为6,21,15?
(4)请尽可能多地画出各直线之间的交点个数不同的图形,从中你能发现什么规律?
23.如图,将三角形ABC向左平移2个单位长度,再向上平移3个单位长度.
(1)画出平移后的三角形A′B′C′;
(2)写出A′,B′,C′的坐标.
24.如图,AD平分∠EAC,AD∥BC,∠C=70°,求∠EAD,∠B的度数.
25.如图,已知OC⊥OB,OA⊥OD,∠1=56°,求∠2.
26.如图,直线AC∥MN∥OB.直线MN上一点P到直线AC、AO、OB的距离相等,即PE=PF=PH.直线AC与MN的距离和直线OB与MN的距离相等吗?请说明理由.
27.已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?
参考答案与试题解析
一.选择题
1.解:任意画三条直线,相交的情况有四种可能:
1、三直线平行,没有交点;
2、三条直线相交于同一点,一个交点;
3、两直线平行被第三直线所截,得到两个交点;
4、两直线相交得到一个交点,又被第三直线所截,共三个交点.
故选:C.
2.解:观察图形知:与∠8互补的角有∠5和∠7,
与∠1互补的角有∠2和∠4,
∵∠1=∠8,
∴与∠8互补的角有4个,
故选:D.
3.解:A、错误,因为线段有端点,所以在同一平面内,两条不平行的线段不一定相交;
B、错误,因为线段有端点,所以不相交的两条线段无法去定其位置关系;
C、正确;
D、错误,与平行于同一条直线的两条直线互相平行的定理相矛盾.
故选:C.
4.解:A、在截线的同侧,并且在被截线之间的两个角是同旁内角,∠2和∠A符合同旁内角的定义,正确;
B、在截线的两侧,并且在被截线之间的两个角是内错角,∠1和∠4符合内错角的定义,正确;
C、在截线的同侧,并且在被截线的之间的两个角是同旁内角,∠2和∠B不符合同旁内角的定义,错误;
D、在截线的同侧,并且在被截线的同一方的两个角是同位角,∠3和∠B符合同位角的定义,正确.
故选:C.
5.解:∵∠1和∠2是内错角,∴由∠1=∠2,得出结论a∥b,其根据是内错角相等,两直线平行.
故选:B.
6.解:∵∠1与∠5是对顶角,
∴∠1=∠2=∠5=45°,
∴a∥b,
∴∠3+∠4=180°,
∵∠3=70°,
∴∠4=110°.
故选:B.
7.解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
8.解:A、∵CE⊥b,FG⊥b,∴FG∥EC,故此选项正确,不符合题意;
B、∵a∥b,FG∥EC,∴四边形FGEC是平行四边形,∴FG=EC,故此选项正确,不符合题意;
C、A、B两点的距离就是线段AB的长,此选项正确,不符合题意;
D、直线a、b间的距离就是线段CE的长,故此选项错误,符合题意.
故选:D.
9.解:A、过已知直线外一点能作已知直线的一条平行线,故本选项错误;
B、过一点能作已知直线的一条垂线,正确;
C、射线AB的端点是A,故本选项错误;
D、点可以用一个大写字母表示,不可用小写字母表示,故本选项错误.
故选:B.
10.解:对题意的分析可知,胶滚上第一行中间为小黑三角形,胶滚从左到右的方向将图案涂到墙上,故第一行应该中间为小黑三角形,所以只有C满足条件.
故选:C.
二.填空题
11.解:如图所示,
∵AB∥CD,
∴∠BGH+∠DHG=180°.
又∵MG、MH分别平分∠BGH和∠DHG,
∴∠1=∠BGH,∠2=∠DHG,
∴∠1+∠2=90°.
∴∠GMH=90°,
故答案为:90°.
12.解:如图,∵∠BOC=2∠AOC,
而∠BOC+∠AOC=180°,
∴2∠AOC+∠AOC=180°,
∴∠AOC=60°,
∴∠BOC=120°,∠BOD=60°,
∴∠AOD=∠BOC=120°,
∵OE为∠AOD的平分线,OF为∠BOD的平分线,
∴∠AOE=∠DOF=∠AOD=60°,∠DOF=∠BOD=30°,
∴∠EOF=∠EOD+∠DOF=90°.
故答案为90°,60°.
13.解:∵∠D+∠C=180°,
∴AD∥BC,
∵∠ABC=90°,
∴∠BAD=90°,
∵AB=10cm,
∴AD与BC的距离是:10cm.
故答案为:10cm.
14.解:点A到直线BC的垂线段是AB,所以线段AB的长是点A到直线BC的距离;
点C到直线AB的垂线段是CB,所以线段CB的长是点C到直线AB的距离.
故填AB,CB.
15.解:∵DE∥AB,
∴∠1=∠BAD,
∵AD⊥BC,
∴∠BAD+∠B=90°,
∴∠1+∠B=90°,
即∠B和∠1的关系是互余,
故答案为:互余.
16.解:所作图形如下所示:
平移前圆心的坐标为(2,﹣1),
沿y轴正向平移4个单位后圆心坐标变为(2,3).
故答案为(2,3).
17.解:如图,a∥b,c与a相交,则c与b必相交,即在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必相交.
18.解:由△ABC是△DEF经过平移得到的,AD=4cm,
则根据平移的性质得:BE=4cm;CF=4cm;
若M为AB的中点,N为DE的中点,则MN=4cm;
若∠B=73°,则∠E=73°.
故答案为:4;4;4;73°.
19.解:∵∠1=∠5=56°,∠2=124°,
∴∠5+∠2=180°,
∴a∥b,
∴∠3+∠4=180°,
∵∠3=85°,
∴∠4=95°.
故答案为:95°
20.解:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也平行.
故填平行.
三.解答题
21.解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
22.解:(1)如图1所示;交点共有6个,
(2)如图2,3.
(3)当n=6时,必须有6条直线平行,都与一条直线相交.如图4,
当n=21时,必须使7条直线中的每2条直线都相交(即无任何两条直线平行)如图5,
当n=15时,如图6,
(4)当我们给出较多答案时,从较多的图形中,可以总结出以下规律:
①当7条直线都相互平行时,交点个数是0,这时交点最少,
②当7条直线每两条均相交时,交点个数为21,这是交点最多.
23.解:(1)△A′B′C′如图所示;
(2)A′(0,4),B′(﹣3,1),C′(0,2).
24.解:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C,
∵AD平分∠EAC,
∴∠EAD=∠DAC,
∵∠C=70°,
∴∠EAD=∠DAC=∠B=∠C=70°.
25.解:∵OA⊥OD,∠1=56°,
∴∠BOD=90°﹣∠1=34°,
∵OC⊥OB,
∴∠2=90°﹣∠BOD=56°.
26.解:相等,
理由是:∵PE、PH的长分别是直线AC与直线MN的距离和直线OB和直线MN间的距离,
又∵PE=PF=PH,
∴直线AC与MN的距离和直线OB与MN的距离相等.
27.解:∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠DCB=180°,
∵AE平分∠BAD,CF平分∠DCB,
∴∠DCF=∠BCF,∠DAE=∠BAE,
∴∠BAE+∠DCF=∠BAD+∠BCD=(∠BAD+∠DCB)=90°.
又∵∠BFC+∠DCF=∠BFC+∠BCF=90°,
∴∠BAE=∠BFC,
∴AE∥CF.
相交线与平行线》单元测试卷
一.选择题
1.任意画三条直线,交点的个数是( )
A.1
B.1或3
C.0或1或2或3
D.不能确定
2.如图所示,直线l1与l2,l3相交,构成的八个角中,已知∠1=∠8,则与∠8互补的角有( )
A.1个
B.2个
C.3个
D.4个
3.下列说法中正确的是( )
A.在同一平面内,两条不平行的线段必相交
B.在同一平面内,不相交的两条线段是平行线
C.两条射线或线段平行是指它们所在的直线平行
D.一条直线有可能同时与两条相交直线平行
4.如图所示,按各组角的位置判断错误的是( )
A.∠2和∠A是同旁内角
B.∠1和∠4是内错角
C.∠2和∠B是同旁内角
D.∠3和∠B是同位角
5.如图,由∠1=∠2,得出结论a∥b,其根据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.在同一平面内垂直于同一条直线的两条直线平行
6.如图,∠1=∠2=45°,∠3=70°,则∠4=( )
A.70°
B.110°
C.45°
D.135°
7.如图所示,AC⊥BC,AD⊥CD,AB=m,CD=n,则AC的取值范围是( )
A.大于n
B.小于m
C.大于n小于m
D.无法确定
8.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,E、G为垂足,则下列说法中错误的是( )
A.CE∥FG
B.CE=FG
C.A、B两点的距离就是线段AB的长
D.直线a、b间的距离就是线段CD的长
9.下列说法正确的是( )
A.过一点能作已知直线的一条平行线
B.过一点能作已知直线的一条垂线
C.射线AB的端点是A和B
D.点可以用一个大写字母表示,也可用小写字母表示
10.小明用所示的胶滚从左到右的方向将图案滚到墙上,正面给出的四个图案中,用图示胶滚涂出的( )
A.
B.
C.
D.
二.填空题
11.若两条平行线被第三条直线所截,则同旁内角的平分线相交所成的角的度数是
.
12.直线AB和CD相交于点O,∠BOC=2∠AOC,OE为∠AOD的平分线,OF为∠BOD的平分线,则∠EOF=
,∠AOE=
.
13.如图,∠ABC=90°,AB=10cm,∠D+∠C=180°,则AD与BC的距离是
.
14.如图,线段
的长是点A到直线BC的距离,线段
的长是点C到直线AB的距离.
15.如图,已知AD⊥BC,垂足为D,DE∥AB交AC于E,那么∠B和∠1的关系是
.
16.如图,将方格中的图案作下列变换,请画出相应的图案:沿y轴正向平移4个单位,并写出平移后圆心的坐标
.
17.在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必
.
18.如图所示,△ABC是△DEF经过平移得到的,若AD=4cm,则BE=
cm,CF=
cm;若点M为AB的中点,点N为DE的中点,则MN=
cm;若∠B=73°,则∠E=
.
19.如图,∠1=56°,∠2=124°,∠3=85°,则∠4=
.
20.在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也
.
三.解答题
21.平面上有9条直线,任意两条都不平行,欲使它们出现29个交点,能否做到,如果能,怎么安排才能做到?如果不能,请说明理由.
22.平面上有7条不同的直线,如果其中任何三条直线都不共点.
(1)请画出满足上述条件的一个图形,并数出图形中各直线之间的交点个数;
(2)请再画出各直线之间的交点个数不同的图形(至少两个);
(3)你能否画出各直线之间的交点个数为n的图形,其中n分别为6,21,15?
(4)请尽可能多地画出各直线之间的交点个数不同的图形,从中你能发现什么规律?
23.如图,将三角形ABC向左平移2个单位长度,再向上平移3个单位长度.
(1)画出平移后的三角形A′B′C′;
(2)写出A′,B′,C′的坐标.
24.如图,AD平分∠EAC,AD∥BC,∠C=70°,求∠EAD,∠B的度数.
25.如图,已知OC⊥OB,OA⊥OD,∠1=56°,求∠2.
26.如图,直线AC∥MN∥OB.直线MN上一点P到直线AC、AO、OB的距离相等,即PE=PF=PH.直线AC与MN的距离和直线OB与MN的距离相等吗?请说明理由.
27.已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?
参考答案与试题解析
一.选择题
1.解:任意画三条直线,相交的情况有四种可能:
1、三直线平行,没有交点;
2、三条直线相交于同一点,一个交点;
3、两直线平行被第三直线所截,得到两个交点;
4、两直线相交得到一个交点,又被第三直线所截,共三个交点.
故选:C.
2.解:观察图形知:与∠8互补的角有∠5和∠7,
与∠1互补的角有∠2和∠4,
∵∠1=∠8,
∴与∠8互补的角有4个,
故选:D.
3.解:A、错误,因为线段有端点,所以在同一平面内,两条不平行的线段不一定相交;
B、错误,因为线段有端点,所以不相交的两条线段无法去定其位置关系;
C、正确;
D、错误,与平行于同一条直线的两条直线互相平行的定理相矛盾.
故选:C.
4.解:A、在截线的同侧,并且在被截线之间的两个角是同旁内角,∠2和∠A符合同旁内角的定义,正确;
B、在截线的两侧,并且在被截线之间的两个角是内错角,∠1和∠4符合内错角的定义,正确;
C、在截线的同侧,并且在被截线的之间的两个角是同旁内角,∠2和∠B不符合同旁内角的定义,错误;
D、在截线的同侧,并且在被截线的同一方的两个角是同位角,∠3和∠B符合同位角的定义,正确.
故选:C.
5.解:∵∠1和∠2是内错角,∴由∠1=∠2,得出结论a∥b,其根据是内错角相等,两直线平行.
故选:B.
6.解:∵∠1与∠5是对顶角,
∴∠1=∠2=∠5=45°,
∴a∥b,
∴∠3+∠4=180°,
∵∠3=70°,
∴∠4=110°.
故选:B.
7.解:∵AC⊥BC,
∴AC<AB,
∵AD⊥CD,
∴AC>CD,
∴CD<AC<AB,
∵AB=m,CD=n,
∴AC的取值范围是:大于n小于m.
故选:C.
8.解:A、∵CE⊥b,FG⊥b,∴FG∥EC,故此选项正确,不符合题意;
B、∵a∥b,FG∥EC,∴四边形FGEC是平行四边形,∴FG=EC,故此选项正确,不符合题意;
C、A、B两点的距离就是线段AB的长,此选项正确,不符合题意;
D、直线a、b间的距离就是线段CE的长,故此选项错误,符合题意.
故选:D.
9.解:A、过已知直线外一点能作已知直线的一条平行线,故本选项错误;
B、过一点能作已知直线的一条垂线,正确;
C、射线AB的端点是A,故本选项错误;
D、点可以用一个大写字母表示,不可用小写字母表示,故本选项错误.
故选:B.
10.解:对题意的分析可知,胶滚上第一行中间为小黑三角形,胶滚从左到右的方向将图案涂到墙上,故第一行应该中间为小黑三角形,所以只有C满足条件.
故选:C.
二.填空题
11.解:如图所示,
∵AB∥CD,
∴∠BGH+∠DHG=180°.
又∵MG、MH分别平分∠BGH和∠DHG,
∴∠1=∠BGH,∠2=∠DHG,
∴∠1+∠2=90°.
∴∠GMH=90°,
故答案为:90°.
12.解:如图,∵∠BOC=2∠AOC,
而∠BOC+∠AOC=180°,
∴2∠AOC+∠AOC=180°,
∴∠AOC=60°,
∴∠BOC=120°,∠BOD=60°,
∴∠AOD=∠BOC=120°,
∵OE为∠AOD的平分线,OF为∠BOD的平分线,
∴∠AOE=∠DOF=∠AOD=60°,∠DOF=∠BOD=30°,
∴∠EOF=∠EOD+∠DOF=90°.
故答案为90°,60°.
13.解:∵∠D+∠C=180°,
∴AD∥BC,
∵∠ABC=90°,
∴∠BAD=90°,
∵AB=10cm,
∴AD与BC的距离是:10cm.
故答案为:10cm.
14.解:点A到直线BC的垂线段是AB,所以线段AB的长是点A到直线BC的距离;
点C到直线AB的垂线段是CB,所以线段CB的长是点C到直线AB的距离.
故填AB,CB.
15.解:∵DE∥AB,
∴∠1=∠BAD,
∵AD⊥BC,
∴∠BAD+∠B=90°,
∴∠1+∠B=90°,
即∠B和∠1的关系是互余,
故答案为:互余.
16.解:所作图形如下所示:
平移前圆心的坐标为(2,﹣1),
沿y轴正向平移4个单位后圆心坐标变为(2,3).
故答案为(2,3).
17.解:如图,a∥b,c与a相交,则c与b必相交,即在同一平面内,一条直线和两条平行线中的一条直线相交,那么这条直线与平行线中的另一条直线必相交.
18.解:由△ABC是△DEF经过平移得到的,AD=4cm,
则根据平移的性质得:BE=4cm;CF=4cm;
若M为AB的中点,N为DE的中点,则MN=4cm;
若∠B=73°,则∠E=73°.
故答案为:4;4;4;73°.
19.解:∵∠1=∠5=56°,∠2=124°,
∴∠5+∠2=180°,
∴a∥b,
∴∠3+∠4=180°,
∵∠3=85°,
∴∠4=95°.
故答案为:95°
20.解:在同一平面内,如果两条直线都和第三条直线平行,那么这两条直线也平行.
故填平行.
三.解答题
21.解:能.理由如下:
9条直线,任意两条都不平行,最多交点的个数是==36,
∵36>29,
∴能出现29个交点,
安排如下:先使4条直线相交于一点P,另外5条直线两两相交最多可得=10个交点,
与前四条直线相交最多可得5×4=20个交点,
让其中两个点重合为点O,所以交点减少1个,
交点个数一共有10+20﹣1=29个.
故能做到.
22.解:(1)如图1所示;交点共有6个,
(2)如图2,3.
(3)当n=6时,必须有6条直线平行,都与一条直线相交.如图4,
当n=21时,必须使7条直线中的每2条直线都相交(即无任何两条直线平行)如图5,
当n=15时,如图6,
(4)当我们给出较多答案时,从较多的图形中,可以总结出以下规律:
①当7条直线都相互平行时,交点个数是0,这时交点最少,
②当7条直线每两条均相交时,交点个数为21,这是交点最多.
23.解:(1)△A′B′C′如图所示;
(2)A′(0,4),B′(﹣3,1),C′(0,2).
24.解:∵AD∥BC,
∴∠EAD=∠B,∠DAC=∠C,
∵AD平分∠EAC,
∴∠EAD=∠DAC,
∵∠C=70°,
∴∠EAD=∠DAC=∠B=∠C=70°.
25.解:∵OA⊥OD,∠1=56°,
∴∠BOD=90°﹣∠1=34°,
∵OC⊥OB,
∴∠2=90°﹣∠BOD=56°.
26.解:相等,
理由是:∵PE、PH的长分别是直线AC与直线MN的距离和直线OB和直线MN间的距离,
又∵PE=PF=PH,
∴直线AC与MN的距离和直线OB与MN的距离相等.
27.解:∵四边形ABCD中,∠B=∠D=90°,
∴∠BAD+∠DCB=180°,
∵AE平分∠BAD,CF平分∠DCB,
∴∠DCF=∠BCF,∠DAE=∠BAE,
∴∠BAE+∠DCF=∠BAD+∠BCD=(∠BAD+∠DCB)=90°.
又∵∠BFC+∠DCF=∠BFC+∠BCF=90°,
∴∠BAE=∠BFC,
∴AE∥CF.
