反比例函数经典题

(共25张PPT)
反比例函数经典题
九年级数学
一. 教学内容：反比例函数
教学目标：
1. 理解反比例函数、图象及其主要性质，能根据所给信息确定反比例函数表达式，画出反比例函数的图象，并利用它们解决简单的实际问题。
2. 初步了解数学在实际生活中的应用，增强应用意识，体会数学的重要性。
二. 重点、难点：
重点：1..能根据所给信息确定反比例函数表达式，画出反比例函数的图象，并利用它们解决简单的实际问题。
2、反比例函数的图像特点及性质的探究
3、通过观察图像，归纳总结反比例函数图像
难点：1、理解反比例函数的概念
2、画反比例函数的图像，并从图像中获取信息
3、从反比例函数的图像中归纳总结反比例函数的主要性质
4.反比例函数的应用。
三、知识要点
1、经历抽象反比例函数概念的过程，并能类推归纳出反比例函数的表达式
2、一般地，如果两个变量x，y之间的关系可以表示成y=（k为常数，k不等于0）的形式，那么称y是x的反比例函数.从y=中可知，x作为分母，所以不能为零
3、画反比例函数图像时要注意以下几点
a 列表时自变量的取值应取绝对值相等而符号相反的一对数值，这样既可以简化计算，又便于标点
b 列表、描点时，要尽量多取一些数值，多描一些点，这样方便连线
c 在连线时要用“光滑的曲线”，不能用折线
4、反比例函数的性质
反比例函数
k的取值范围
图象
性质 ①的取值范围是，的取值范围是②函数图象的两个分支分别在第一、三象限，在每一个象限内随的增大而减小 ①的取值范围是，的取值范围是②函数图象的两个分支分别在第二、四象限，在每一个象限内随的增大而增大
注意：1）反比例函数是轴对称图形和中心对称图形；
2）双曲线的两个分支都与轴、轴无限接近，但永远不能与坐标轴相交；3）在利用图象性质比较函数值的大小时，前提应是“在同一象限”内。
5、反比例函数系数的几何意义
如图，过双曲线上任意一点P作 轴， 轴的垂线PM，PN，所得矩形的面积为
∵ ∴ ∴ ，
即过双曲线上任一点作 轴， 轴的垂线，所得矩形的面积为
注意：①若已知矩形的面积为 ，应根据双曲线的位置确定k值的符号。
②在一个反比例函数图象上任取两点P，Q，分别过P，Q作x轴、y轴的平行线，与坐标轴围成的矩形面积为S1，S2，则有S1＝S2。
四、典例解析
考点一、反比例函数的定义
例1、用电器的输出功率P与通过的电流I，用电器的电阻R之间的关系是，下面说法正确的是（ ）
A. P为定值，I与R成反比例
B. P为定值，I^与R成反比例
C. P为定值，I与R成正比例
D. P为定值，与R成正比例
本题的答案是：B
例2、 为何值时， 是反比例函数？
解：
常见的错误：
1）不会把反比例函数的一般形式 写成 形式 ；
2）忽略了 这个条件。
考点二：反比例函数的图象
例3、若 三点都在函数 的图象上，则 的大小关系是（ ）
A. B. C. D.
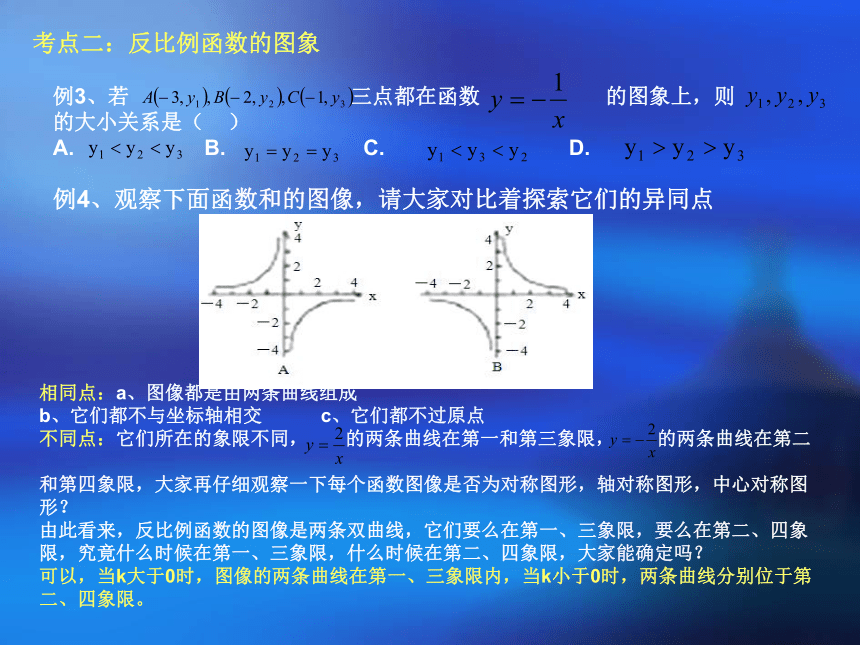
例4、观察下面函数和的图像，请大家对比着探索它们的异同点
相同点：a、图像都是由两条曲线组成
b、它们都不与坐标轴相交 c、它们都不过原点
不同点：它们所在的象限不同， 的两条曲线在第一和第三象限， 的两条曲线在第二
和第四象限，大家再仔细观察一下每个函数图像是否为对称图形，轴对称图形，中心对称图形？
由此看来，反比例函数的图像是两条双曲线，它们要么在第一、三象限，要么在第二、四象限，究竟什么时候在第一、三象限，什么时候在第二、四象限，大家能确定吗？
可以，当k大于0时，图像的两条曲线在第一、三象限内，当k小于0时，两条曲线分别位于第二、四象限。
例5、已知反比例函数 ，分别根据以下条件求出 的取值范围。
（1）函数图象位于第一、三象限内；
（2）在每一个象限内， 随 的增大而增大。
例6、如图，反比例函数图像上任取两点P、Q，过点P分别作x轴，y轴的平行线与坐标轴围成的矩形面积为 ，过点Q分别作x轴，y轴的平行线，与坐标轴围成的矩形面积为 。
（1） 与 有什么关系？为什么？
（2）将反比例函数的图像绕原点旋转180度后，能与原来的图像重合吗？
5、解：（1）∵双曲线在第一、三象限内，∴
（2）∵在每一个象限内 随 的增大而增大 ∴
6、解：（1）①P、Q两点在同一条曲线上：
设P（ ），过P点分别作x轴、y轴的平行线，与两坐标轴围成的矩形面积为 ，则
因为（ ）在反比例函数 的图像上，所以
即 所以
同理可知 所以 =
②P、Q分别在不同的曲线上：
解法同1
同理可知 = 因此只要是在同一个反比例函数
图像上任取两点P、Q，不管P、Q是在同一条曲线上，
还是在不同的曲线上，过P、Q分别作x轴，y轴的平行线与坐标轴围成的矩形面积、都有=
（2）若将反比例函数的图像绕原点旋转180度后，能与原来的图像重合. 因为反比例函数既是轴对称图形又是中心对称图形。
例7、小明将一篇24000字的社会调查报告录入电脑，打印成文.
（1）如果小明以每分钟120字的速度录入，他需要多长时间才能完成录入任务？
（2）录入文字的速度v（字/min）与完成录入的时间t（min）有怎样的函数关系．
（3）小明希望能在3h内完成录入任务，那么他每分钟至少应录入多少个字？
例9、反比例函数的图象上有一点P（m，n）其坐标是关于t的一元二次方程 的两根，且P到原点的距离为 ，求该反比例函数的解析式.
7、分析：题中的等量关系为：总字数=录入文字的速度×录入时间
解：（1）24000÷120=200（分钟） 所以他需要用200分钟才能完成录入工作。
（2）函数关系式是： （3）3h=180min
由于录入的字要为整数，所以他每分钟至少要录入134个字。
9、分析：要求反比例函数的解析式，就是要求出k，为此我们需要列出一个关于k的方程.
解：∵ m，n是关于t的方程 的两根 ∴ m+n=3，mn=k，
又 PO= ∴
∴
∴ 9－2k=13.
∴ k=－2 当 k=－2时，△=9+8＞0，
∴ k=－2符合条件， ∴反比例函数的解析式为：
考点六：反比例函数与一次函数的应用
例10、如图，一次函数的图象与反比例函数的图象相交于A、B两点。
（1）根据图象，写出B点的坐标；（2）求出两函数的解析式；
（3）根据图象回答：当为何值时，一次函数的函数值大于反比例函数的值。
考点六：反比例函数与一次函数的应用
例10、如图，一次函数的图象与反比例函数的图象相交于A、B两点。
（1）根据图象，写出B点的坐标；（2）求出两函数的解析式；
（3）根据图象回答：当为何值时，一次函数的函数值大于反比例函数的值。
解：（1）由图象可得B（4，3）
（2）把反比例函数上的点代入函数的关系式 得
∴反比例函数的关系式为
由图可知一次函数与坐标轴的交点为（0，1）和（－2，0）
把这两点代入一次函数关系式+b得：
解得： ∴一次函数的关系式为：
（3）由图象可知，当 时，一次函数的函数值大于反比例函数的函数值
例11、如图，平行于直线 的直线 不经过第四象限，且与函数 的图象交于点A，过点A作AB⊥ 轴于点B，AC⊥ 轴于点C，四边形ABOC的周长是8，求直线 的解析式。
例11、如图，平行于直线 的直线 不经过第四象限，且与函数 的图象交于点A，过点A作AB⊥ 轴于点B，AC⊥ 轴于点C，四边形ABOC的周长是8，求直线 的解析式。
解：∵点A在函数 的图象上，
∴设A点的横坐标为 ，由点A的纵坐标为 ，即A点的坐标为
∵AB⊥ 轴于点B，AC⊥ 轴于点C，∠BOC=90°
∴四边形ABOC是矩形，∵四边形ABOC的周长是8，
∴ 即
解得
当
∴A点坐标为（1，3）或（3，1）（由题意可知 ）∴A点坐标为（1，3）
设直线 的解析式为 把A点代入 得
3=1+b b=2 ∴直线的解析式为
一、选择题
1. 下列不是反比例函数图象的特点的是 （ ）
A. 图象是由两部分构成
B. 图象与坐标轴无交点
C. 图象要么总向右上方，要么总向右下方
D. 图象与坐标轴相交而成的一对对顶角内
2. 若点（3，6）在反比例函数 （k≠0）的图象上，那么下列各点在此图象上的是（ ）
A. （ ，6） B. （2，9） C. （2， ） D. （3， ）
*3. 当 时，下列图象中表示函数 的图象的是 （ ）
4. 如果x与y满足 ，则y是x的 （ ）
A. 正比例函数 B. 反比例函数 C. 一次函数 D. 二次函数
5. 已知反比例函数的图象过（2，－2）和（－1，n），则n等于 （ ）
A. 3 B. 4 C. 6 D. 12
6. 已知某县的粮食产量为a（a为常数）吨，设该县平均每人粮食产量为y吨，人口数为x，则y与x之间的函数关系的图象可能是下图中的 （ ）
7. 若ab＜0，则函数 与 在同一坐标系内的图象大致可能是下图中的（ ）
8、下列函数中， 是 反比例函数的是（ ）
A. B. C. D.
9、函数y1=kx和 的图象如图所示，自变量x的取值范围相同的是（ ）
10、函数 与 在同一平面直角坐标系中的图像可能是（ ）。
11、反比例函数 （k≠0）的图象的两个分支分别位于（ ）象限。
A. 一、二 B. 一、三 C. 二、四 D. 一、四　
12、当三角形的面积一定时，三角形的底和底边上的高成（ ）关系。
A. 正比例函数 B. 反比例函数 C. 一次函数 D. 二次函数
13、函数 与 的图象可能是（ ）
14、如图，是三个反比例函数 在x轴上的图像，由此观察得到k1、k2、k3的大小关系为（ ）
A. k1>k2>k3 B. k1>k3>k2 C. k2>k3>k1 D. k3>k2>k1
15、已知双曲线 上有一点P（m，n），且m、n是关于t的一元二次方程t2－3t+k=0的两根，P点到原点的距离为 ，则双曲线的表达式为（ ）
A. B. C. D.
16、如图，正比例函数y=x与反比例函数 的图象相交于A、C两点，AB⊥x轴于B，CD⊥x轴于D，则四边形ABCD的面积为（ ）
A. 1 B. C. 2 D.
17、如图，已知点A是一次函数y=x的图象与反比例函数 的图象在第一象限内的交点，点B在x轴的负半轴上，且OA=OB，那么△AOB的面积为
A. 2 B. C. D.
二、填空题
1. 反比例函数 （k≠0）的图象是__________，当k＞0时，图象的两个分支分别在第__________、__________象限内，在每一个象限内，y随x的增大而__________；当k＜0时，图象的两个分支分别在第__________、__________象限内，在每一个象限内，y随x的增大而__________；
*2. 已知函数 ，当x＜0时，y_______0，此时，其图象的相应部分在第_______象限；
*3. 当 时，双曲线y= 过点（ ，2 ）；
4. 已知 （k≠0）的图象的一部分如图，则 ；
5. 如图，若反比例函数 的图象过点A，则该函数的解析式为__________；
*6. 若A（x1，y1），B（x2，y2），C（x3，y3）都是反比例函数 的图象上的点，且x1＜0＜x2＜x3，则y1，y2，y3由小到大的顺序是 ；
*7、已知y与（2x+1）成反比例且当x=0时，y=2，那么当x=－1时，y=________。
8、如果反比例函数 的图象经过点（3，1），那么k=_______。
9、函数 与y=－2x的图象的交点坐标是____________。
10、已知一次函数y=ax+b图象在一、二、三象限，则反比例函数y= 的函数值随x的增大而__________。
11、已知 ，那么y与x成_________比例，k=________，其图象在第_______象限。
*12、反比例函数 ，当x＞0时，y随x的增大而增大，则m的值是 。
三、解答题
1. 已知反比例函数 ，分别根据下列条件求k的取值范围，并画出草图.
（1）函数图象位于第一、三象限.（2）函数图象的一个分支向右上方延伸.
2. 已知y与x的部分取值满足下表：
x －6 －5 －4 －3 －2 －1 2 3 4 5 6 ……
y 1 1.2 1.5 2 3 6 －3 －2 －1.5 －1.2 －1 ……
（1）试猜想y与x的函数关系可能是你们学过的哪类函数，并写出这个函数的解析式.（不要求写x的取值范围） （2）简要叙述该函数的性质.
3、直线 过x轴上的点A（ ，0），且与双曲线 相交于B、C两点，已知B点坐标为（ ，4），求直线和双曲线的解析式。
4、已知一次函数 与反比例函数 的图象的一个交点为P（a，b），且P到原点的距离是10，求a、b的值及反比例函数的解析式。
5、已知函数 是一次函数，它的图象与反比例函数 的图象交于一点，交点的横坐标是 ，求反比例函数的解析式。
6、已知反比例函数 的图象经过点A（4， ），若一次函数y=x+1的图象沿x轴平移后经过该反比例函数图象上的点B（2，m），求平移后的一次函数图象与x轴的交点坐标？