2020—2021学年人教版数学八年级下册 第十八章 平行四边形 习题练习(word版含答案)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册 第十八章 平行四边形 习题练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 79.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 20:35:47 | ||
图片预览



文档简介
人教版数学八年级下册
第十八章
平行四边形
习题练习(附答案)
一、选择题
1.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.
150°B.
130°
C.
120°D.
100°
2.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE
B.BE⊥DC
C.
∠ADB=90°
D.CE⊥DE
3.菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A.
2
B.
C.
6
D.
8
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )
A.AB=BE
B.AC=2AB
C.AB=2OE
D.AC=2OE
5.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.
①,②B.
①,④
C.
③,④D.
②,③
6.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A.
1
B.
C.
2-
D.
2-2
7.在如图的方格纸中有一个菱形ABCD(A,B,C,D四点均为格点),若方格纸中每个最小正方形的边长为1,则该菱形的面积为( )
A.
8
B.
10
C.
12
D.
14
8.在平行四边形ABCD中,∠A∶∠B∶∠C=2∶3∶2,则∠D等于( )
A.
36°
B.
108°
C.
72°
D.
60°
9.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A.BD=AE
B.CB=BF
C.BE⊥CF
D.BA平分∠CBF
10.给定平面上不在同一直线上的三点,以这三点为顶点的平行四边形有( )
A.
4个B.
3个
C.
2个D.
1个
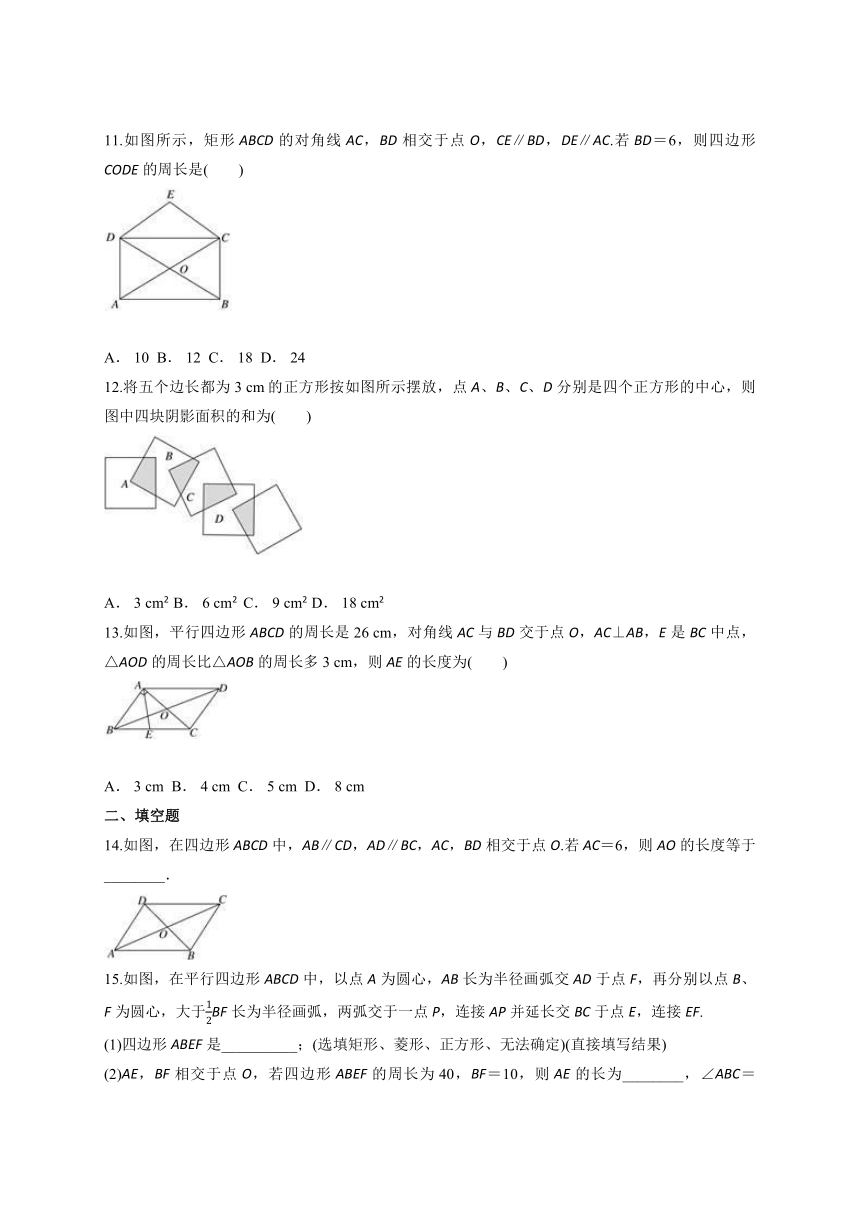
11.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.
10
B.
12
C.
18
D.
24
12.将五个边长都为3
cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
A.
3
cm2
B.
6
cm2
C.
9
cm2
D.
18
cm2
13.如图,平行四边形ABCD的周长是26
cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3
cm,则AE的长度为( )
A.
3
cm
B.
4
cm
C.
5
cm
D.
8
cm
二、填空题
14.如图,在四边形ABCD中,AB∥CD,AD∥BC,AC,BD相交于点O.若AC=6,则AO的长度等于________.
15.如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是__________;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=____________°.(直接填写结果)
16.如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC上,且∠EOF=90°,则S四边形OEBF∶S正方形ABCD=__________.
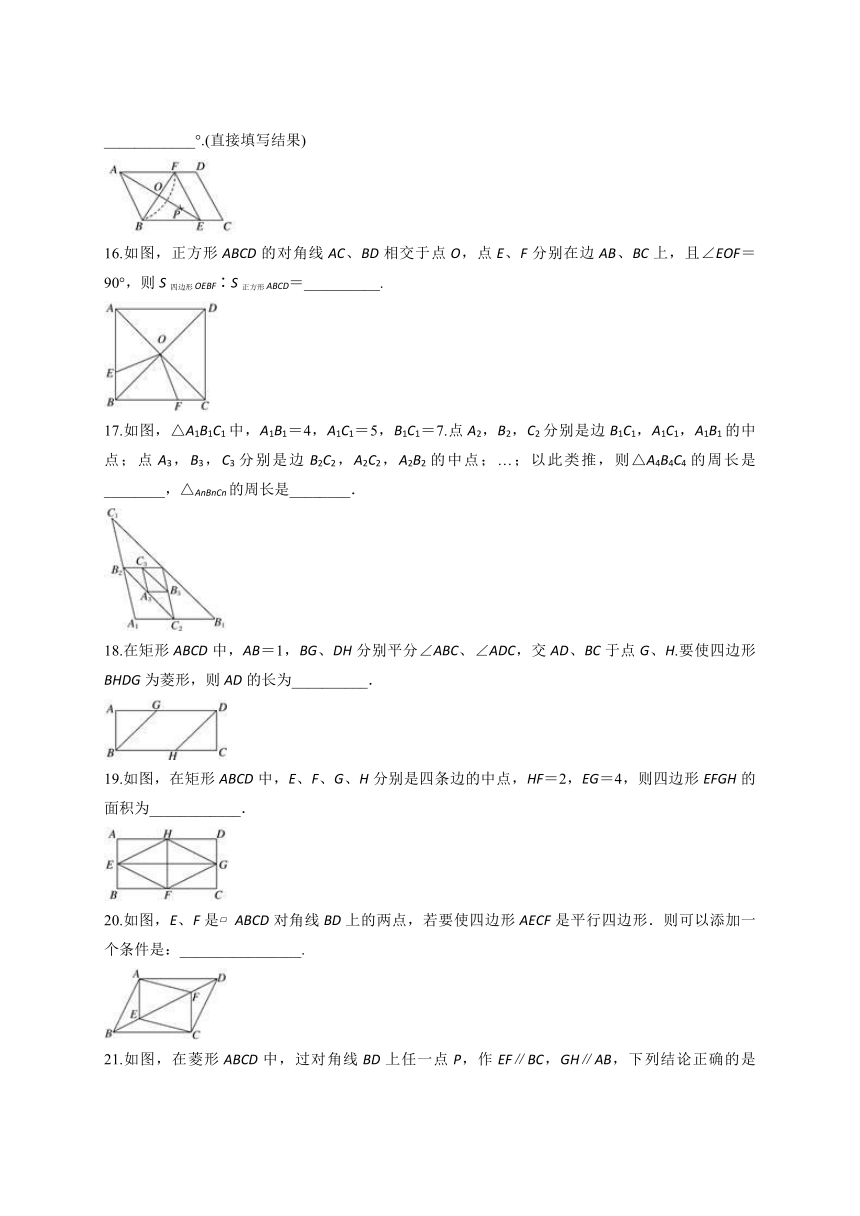
17.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则△A4B4C4的周长是________,△AnBnCn的周长是________.
18.在矩形ABCD中,AB=1,BG、DH分别平分∠ABC、∠ADC,交AD、BC于点G、H.要使四边形BHDG为菱形,则AD的长为__________.
19.如图,在矩形ABCD中,E、F、G、H分别是四条边的中点,HF=2,EG=4,则四边形EFGH的面积为____________.
20.如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:________________.
21.如图,在菱形ABCD中,过对角线BD上任一点P,作EF∥BC,GH∥AB,下列结论正确的是________________.(填序号)
①图中共有3个菱形;
②△BEP≌△BGP;
③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
三、解答题
22.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
23.如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
24.如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
答案解析
1.【答案】C
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∵∠BED=150°,
∴∠ABE=∠AEB=30°,
∴∠A=180°-∠ABE-∠AEB=120°.
故选C.
2.【答案】B
【解析】∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵AD=DE,
∴DE∥BC,且DE=BC,
∴四边形BCED为平行四边形,
A.∵AB=BE,DE=AD,∴BD⊥AE,∴?DBCE为矩形,故本选项错误;
B.∵对角线互相垂直的平行四边形为菱形,不一定为矩形,故本选项正确;
C.∵∠ADB=90°,∴∠EDB=90°,∴?DBCE为矩形,故本选项错误;
D.∵CE⊥DE,∴∠CED=90°,∴?DBCE为矩形,故本选项错误.
故选B.
3.【答案】A
【解析】∵E,F分别是AD,CD边上的中点,EF=,
∴AC=2EF=2,
又∵BD=2,
∴菱形ABCD的面积S=×AC×BD=×2×2=2,
故选A.
4.【答案】C
【解析】∵点E为BC的中点,
∴CE=BE=BC,
∵AB=BC,
∴AB=2BE,故选项A错误;
∵在菱形ABCD中,对角线AC,BD相交于点O,
∴AO=CO=AC,
∴OE是△ABC的中位线,
∴OE=AB,故选项C正确;
∵AC≠AB≠BC,
∴AC≠2AB≠2OE,故选项B,D错误,
故选C.
5.【答案】D
【解析】∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
6.【答案】C
【解析】∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=,由折叠易得△ABB′为等腰直角三角形,
∴S△ABB′=BA·AB′=2,S△ABE=1,
∴CB′=2BE-BC=2-2,
∵AB∥CD,
∴∠FCB′=∠B=45°,
又由折叠的性质知,∠B′=∠B=45°,
∴CF=FB′=2-.
故选C.
7.【答案】C
【解析】读图可得,菱形的两对角线长分别为6、4,则该菱形的面积为6×4×=12.故选C.
8.【答案】B
【解析】在?ABCD中,∠A∶∠B∶∠C∶∠D=2∶3∶2∶3,
设每份比为x,则得到2x+3x+2x+3x=360°,
解得x=36°
则∠D=108°.
故选B.
9.【答案】A
【解析】根据题意可得出:四边形CBFE是平行四边形,
A.当BD=AE时,无法得出平行四边形CBFE是菱形,故选项A错误,符合题意;
B.当CB=BF时,平行四边形CBFE是菱形,故选项B正确,不合题意;
C.当BE⊥CF时,平行四边形CBFE是菱形,故选项C正确,不合题意;
D.当BA平分∠CBF时,平行四边形CBFE是菱形,故选项D正确,不合题意;
故选A.
10.【答案】B
【解析】如图所示:
以点A,B,C为顶点能做三个平行四边形:?ABCD,?ABFC,?AEBC.
故选B.
11.【答案】B
【解析】∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=AC,OD=BD,AC=BD=6,
∴OC=OD=3,
∴四边形CODE是菱形,
∴DE=OC=OD=CE=3,
∴四边形CODE的周长=4×3=12.
12.【答案】C
【解析】如图AB、AF.
∵∠EAG=∠BAF=90°,
∴∠BAE=∠FAG,
在△ABE和△AFG中,
∴△ABE≌△AFG,
∴S△ABE=S△AFG,
∴S四边形AEBG=S△ABF=S正方形,
∴S阴=4×S正方形=9,
故选C.
13.【答案】B
【解析】∵?ABCD的周长为26
cm,
∴AB+AD=13
cm,OB=OD,
∵△AOD的周长比△AOB的周长多3
cm,
∴(OA+OD+AD)-(OA+OB+AB)=AD-AB=3
cm,
∴AB=5
cm,AD=8
cm.
∴BC=AD=8
cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4
cm;
故选B.
14.【答案】3
【解析】∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AO=CO=AC,
∵AC=6,
∴AO=3.
15.【答案】(1)菱形 (2)10 120
【解析】(1)在△AEB和△AEF中,
∴△AEB≌△AEF,
∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形
∵AB=AF,
∴四边形ABEF是菱形.
故答案为菱形.
(2)∵四边形ABEF是菱形,
∴AE⊥BF,BO=OF=5,∠ABO=∠EBO,
∵AB=10,
∴AB=2BO,∵∠AOB=90°
∴∠BAO=30°,∠ABO=60°,
∴AO=BO=5,∠ABC=2∠ABO=120°.
故答案为10,120.
16.【答案】
【解析】∵四边形ABCD是正方形,
∴OA=OB,∠EAO=∠FBO=45°,
又∵∠AOE+∠EOB=90°,∠BOF+∠EOB=90°,
∴∠AOE=∠BOF,
在△AOE与△BOF中,
∴△AEO≌△BFO,
∴AE=BF,
∴BE=CF,
∴S四边形OEBF=S△AOB,
∴S四边形OEBF∶S正方形ABCD=,
17.【答案】2
【解析】∵△A1B1C1中,A1B1=4,A1C1=5,B1C1=7,
∴△A1B1C1的周长是16,
∵A2,B2,C2分别是边B1C1,A1C1,A1B1的中点,
∴B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的,
…,
以此类推,则△A4B4C4的周长是×16=2;
∴△AnBnCn的周长是.
18.【答案】1+
【解析】∵在矩形ABCD中,BG平分∠ABC,
∴∠A=90°,∠ABG=45°,
∴∠AGB=∠ABG=45°,
∴AB=AG.
又∵AB=1,
∴BG=.
又∵四边形BHDG为菱形,
∴BG=GD=.
∴AD=AG+GD=1+.
19.【答案】4
【解析】∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,
∵E、F、G、H分别是四条边的中点,
∴AE=DG=BE=CG,AH=DH=BF=CF,
∴△AEH≌△DGH≌△BEF≌△CGF(SAS),
∴EH=EF=FG=GH,
∴四边形EFGH是菱形,
∵HF=2,EG=4,
∴四边形EFGH的面积为HF·EG=×2×4=4.
20.【答案】BE=DF(答案不唯一)
【解析】可添加条件:BE=DF.
证明:∵?ABCD,
∴AB=CD,∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF,
∴AE=CF,
同理可证:△ADF≌△CBE,
∴AF=CE,
∴四边形AECF是平行四边形.
故答案为BE=DF.
21.【答案】①②④
【解析】∵图中有三个菱形,如菱形ABCD、菱形HPFD、菱形BEPG,∴①正确;
∵四边形ABCD是菱形,
∴AB∥DC,AD∥BC,∠ABD=∠CBD,
∵EF∥BC,GH∥AB,
∴四边形BEPG是平行四边形,
∴PE=BG,PG=BE,
在△BEP和△PGB中,
∴△BEP≌△PGB(SSS),
∴②正确;
∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;
∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EF∥BC,GH∥AB,
∴AD∥EF∥BC,AB∥GH∥CD,
∴四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,
∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=CG,
∵四边形ABCD是菱形,
∴∠EBP=∠GBP,∵PE∥BG,
∴∠EPB=∠GBP,∴∠EBP=∠EPB,
∴BE=PE,∴AH=PE=BG=BE=CF=PG,
同理AE=HP=DF=PF=CG,
∴四边形AEPH的周长=四边形GPFC的周长,∴④正确;
22.【答案】(1)证明 ∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
∴Rt△ADF≌Rt△ABE(HL)
∴BE=DF,
∵BC=DC,
∴CE=CF;
(2)解 四边形AEMF是菱形,理由:
∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,
在△COE和△COF中,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴平行四边形AEMF是菱形.
【解析】(1)求简单的线段相等,可证线段所在的三角形全等,即证△ABE≌△ADF;
(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相平分,再根据一组邻边相等的平行四边形是菱形,即可判定四边形AEMF是菱形.
23.【答案】证明 ∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),
∴AE=CF.
【解析】根据平行四边形的性质得出AB=CD,AB∥CD,根据平行线的性质得出∠ABE=∠CDF,求出∠AEB=∠CFD=90°,根据AAS推出△ABE≌△CDF,得出对应边相等即可.
24.【答案】证明 (1)由平行四边形ABCD,得AD∥BC,AD=BC,∠ADF=∠CBE,
∵AM=CN,
∴AD-AM=BC-CN,
即DM=BN,
又∵DF=BE,
∴△DMF≌△BNE,
∴∠DFM=∠BEN;
(2)由△DMF≌△BNE,得NE=MF,
∵∠DFM=∠BEN,∴∠FEN=∠MFE,
∴MF∥NE,
∴四边形NEMF是平行四边形.
【解析】(1)由平行四边形的性质得到得AD∥BC,AD=BC,∠ADF=∠CBE,然后根据AM=CN得到DM=BN,从而证得△DMF≌△BNE,理由全等三角形对应角相等证得结论;
(2)利用一组对边平行且相等的四边形为平行四边形进行判定即可.
第十八章
平行四边形
习题练习(附答案)
一、选择题
1.如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小为( )
A.
150°B.
130°
C.
120°D.
100°
2.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE
B.BE⊥DC
C.
∠ADB=90°
D.CE⊥DE
3.菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为( )
A.
2
B.
C.
6
D.
8
4.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC的中点,则下列等式中一定成立的是( )
A.AB=BE
B.AC=2AB
C.AB=2OE
D.AC=2OE
5.小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )
A.
①,②B.
①,④
C.
③,④D.
②,③
6.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为( )
A.
1
B.
C.
2-
D.
2-2
7.在如图的方格纸中有一个菱形ABCD(A,B,C,D四点均为格点),若方格纸中每个最小正方形的边长为1,则该菱形的面积为( )
A.
8
B.
10
C.
12
D.
14
8.在平行四边形ABCD中,∠A∶∠B∶∠C=2∶3∶2,则∠D等于( )
A.
36°
B.
108°
C.
72°
D.
60°
9.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A.BD=AE
B.CB=BF
C.BE⊥CF
D.BA平分∠CBF
10.给定平面上不在同一直线上的三点,以这三点为顶点的平行四边形有( )
A.
4个B.
3个
C.
2个D.
1个
11.如图所示,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.
10
B.
12
C.
18
D.
24
12.将五个边长都为3
cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
A.
3
cm2
B.
6
cm2
C.
9
cm2
D.
18
cm2
13.如图,平行四边形ABCD的周长是26
cm,对角线AC与BD交于点O,AC⊥AB,E是BC中点,△AOD的周长比△AOB的周长多3
cm,则AE的长度为( )
A.
3
cm
B.
4
cm
C.
5
cm
D.
8
cm
二、填空题
14.如图,在四边形ABCD中,AB∥CD,AD∥BC,AC,BD相交于点O.若AC=6,则AO的长度等于________.
15.如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于BF长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
(1)四边形ABEF是__________;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=____________°.(直接填写结果)
16.如图,正方形ABCD的对角线AC、BD相交于点O,点E、F分别在边AB、BC上,且∠EOF=90°,则S四边形OEBF∶S正方形ABCD=__________.
17.如图,△A1B1C1中,A1B1=4,A1C1=5,B1C1=7.点A2,B2,C2分别是边B1C1,A1C1,A1B1的中点;点A3,B3,C3分别是边B2C2,A2C2,A2B2的中点;…;以此类推,则△A4B4C4的周长是________,△AnBnCn的周长是________.
18.在矩形ABCD中,AB=1,BG、DH分别平分∠ABC、∠ADC,交AD、BC于点G、H.要使四边形BHDG为菱形,则AD的长为__________.
19.如图,在矩形ABCD中,E、F、G、H分别是四条边的中点,HF=2,EG=4,则四边形EFGH的面积为____________.
20.如图,E、F是?ABCD对角线BD上的两点,若要使四边形AECF是平行四边形.则可以添加一个条件是:________________.
21.如图,在菱形ABCD中,过对角线BD上任一点P,作EF∥BC,GH∥AB,下列结论正确的是________________.(填序号)
①图中共有3个菱形;
②△BEP≌△BGP;
③四边形AEPH的面积等于△ABD的面积的一半;
④四边形AEPH的周长等于四边形GPFC的周长.
三、解答题
22.如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:CE=CF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
23.如图,BD是?ABCD的对角线,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:AE=CF.
24.如图,已知平行四边形ABCD,点M,N分别在边AD和边BC上,点E,F在线段BD上,且AM=CN,DF=BE.求证:
(1)∠DFM=∠BEN;
(2)四边形MENF是平行四边形.
答案解析
1.【答案】C
【解析】∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∵∠BED=150°,
∴∠ABE=∠AEB=30°,
∴∠A=180°-∠ABE-∠AEB=120°.
故选C.
2.【答案】B
【解析】∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC,
又∵AD=DE,
∴DE∥BC,且DE=BC,
∴四边形BCED为平行四边形,
A.∵AB=BE,DE=AD,∴BD⊥AE,∴?DBCE为矩形,故本选项错误;
B.∵对角线互相垂直的平行四边形为菱形,不一定为矩形,故本选项正确;
C.∵∠ADB=90°,∴∠EDB=90°,∴?DBCE为矩形,故本选项错误;
D.∵CE⊥DE,∴∠CED=90°,∴?DBCE为矩形,故本选项错误.
故选B.
3.【答案】A
【解析】∵E,F分别是AD,CD边上的中点,EF=,
∴AC=2EF=2,
又∵BD=2,
∴菱形ABCD的面积S=×AC×BD=×2×2=2,
故选A.
4.【答案】C
【解析】∵点E为BC的中点,
∴CE=BE=BC,
∵AB=BC,
∴AB=2BE,故选项A错误;
∵在菱形ABCD中,对角线AC,BD相交于点O,
∴AO=CO=AC,
∴OE是△ABC的中位线,
∴OE=AB,故选项C正确;
∵AC≠AB≠BC,
∴AC≠2AB≠2OE,故选项B,D错误,
故选C.
5.【答案】D
【解析】∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选D.
6.【答案】C
【解析】∵在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,
∴AE=,由折叠易得△ABB′为等腰直角三角形,
∴S△ABB′=BA·AB′=2,S△ABE=1,
∴CB′=2BE-BC=2-2,
∵AB∥CD,
∴∠FCB′=∠B=45°,
又由折叠的性质知,∠B′=∠B=45°,
∴CF=FB′=2-.
故选C.
7.【答案】C
【解析】读图可得,菱形的两对角线长分别为6、4,则该菱形的面积为6×4×=12.故选C.
8.【答案】B
【解析】在?ABCD中,∠A∶∠B∶∠C∶∠D=2∶3∶2∶3,
设每份比为x,则得到2x+3x+2x+3x=360°,
解得x=36°
则∠D=108°.
故选B.
9.【答案】A
【解析】根据题意可得出:四边形CBFE是平行四边形,
A.当BD=AE时,无法得出平行四边形CBFE是菱形,故选项A错误,符合题意;
B.当CB=BF时,平行四边形CBFE是菱形,故选项B正确,不合题意;
C.当BE⊥CF时,平行四边形CBFE是菱形,故选项C正确,不合题意;
D.当BA平分∠CBF时,平行四边形CBFE是菱形,故选项D正确,不合题意;
故选A.
10.【答案】B
【解析】如图所示:
以点A,B,C为顶点能做三个平行四边形:?ABCD,?ABFC,?AEBC.
故选B.
11.【答案】B
【解析】∵CE∥BD,DE∥AC,
∴四边形CODE是平行四边形,
∵四边形ABCD是矩形,
∴OC=AC,OD=BD,AC=BD=6,
∴OC=OD=3,
∴四边形CODE是菱形,
∴DE=OC=OD=CE=3,
∴四边形CODE的周长=4×3=12.
12.【答案】C
【解析】如图AB、AF.
∵∠EAG=∠BAF=90°,
∴∠BAE=∠FAG,
在△ABE和△AFG中,
∴△ABE≌△AFG,
∴S△ABE=S△AFG,
∴S四边形AEBG=S△ABF=S正方形,
∴S阴=4×S正方形=9,
故选C.
13.【答案】B
【解析】∵?ABCD的周长为26
cm,
∴AB+AD=13
cm,OB=OD,
∵△AOD的周长比△AOB的周长多3
cm,
∴(OA+OD+AD)-(OA+OB+AB)=AD-AB=3
cm,
∴AB=5
cm,AD=8
cm.
∴BC=AD=8
cm.
∵AC⊥AB,E是BC中点,
∴AE=BC=4
cm;
故选B.
14.【答案】3
【解析】∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∴AO=CO=AC,
∵AC=6,
∴AO=3.
15.【答案】(1)菱形 (2)10 120
【解析】(1)在△AEB和△AEF中,
∴△AEB≌△AEF,
∴∠EAB=∠EAF,
∵AD∥BC,
∴∠EAF=∠AEB=∠EAB,
∴BE=AB=AF.
∵AF∥BE,
∴四边形ABEF是平行四边形
∵AB=AF,
∴四边形ABEF是菱形.
故答案为菱形.
(2)∵四边形ABEF是菱形,
∴AE⊥BF,BO=OF=5,∠ABO=∠EBO,
∵AB=10,
∴AB=2BO,∵∠AOB=90°
∴∠BAO=30°,∠ABO=60°,
∴AO=BO=5,∠ABC=2∠ABO=120°.
故答案为10,120.
16.【答案】
【解析】∵四边形ABCD是正方形,
∴OA=OB,∠EAO=∠FBO=45°,
又∵∠AOE+∠EOB=90°,∠BOF+∠EOB=90°,
∴∠AOE=∠BOF,
在△AOE与△BOF中,
∴△AEO≌△BFO,
∴AE=BF,
∴BE=CF,
∴S四边形OEBF=S△AOB,
∴S四边形OEBF∶S正方形ABCD=,
17.【答案】2
【解析】∵△A1B1C1中,A1B1=4,A1C1=5,B1C1=7,
∴△A1B1C1的周长是16,
∵A2,B2,C2分别是边B1C1,A1C1,A1B1的中点,
∴B2C2,A2C2,A2B2分别等于A1B1、B1C1、C1A1的,
…,
以此类推,则△A4B4C4的周长是×16=2;
∴△AnBnCn的周长是.
18.【答案】1+
【解析】∵在矩形ABCD中,BG平分∠ABC,
∴∠A=90°,∠ABG=45°,
∴∠AGB=∠ABG=45°,
∴AB=AG.
又∵AB=1,
∴BG=.
又∵四边形BHDG为菱形,
∴BG=GD=.
∴AD=AG+GD=1+.
19.【答案】4
【解析】∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠B=∠C=∠D=90°,
∵E、F、G、H分别是四条边的中点,
∴AE=DG=BE=CG,AH=DH=BF=CF,
∴△AEH≌△DGH≌△BEF≌△CGF(SAS),
∴EH=EF=FG=GH,
∴四边形EFGH是菱形,
∵HF=2,EG=4,
∴四边形EFGH的面积为HF·EG=×2×4=4.
20.【答案】BE=DF(答案不唯一)
【解析】可添加条件:BE=DF.
证明:∵?ABCD,
∴AB=CD,∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF,
∴AE=CF,
同理可证:△ADF≌△CBE,
∴AF=CE,
∴四边形AECF是平行四边形.
故答案为BE=DF.
21.【答案】①②④
【解析】∵图中有三个菱形,如菱形ABCD、菱形HPFD、菱形BEPG,∴①正确;
∵四边形ABCD是菱形,
∴AB∥DC,AD∥BC,∠ABD=∠CBD,
∵EF∥BC,GH∥AB,
∴四边形BEPG是平行四边形,
∴PE=BG,PG=BE,
在△BEP和△PGB中,
∴△BEP≌△PGB(SSS),
∴②正确;
∵只有当H为AD中点,E为AB中点时,四边形AEPH的面积等于△ABD的面积的一半,∴③错误;
∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∵EF∥BC,GH∥AB,
∴AD∥EF∥BC,AB∥GH∥CD,
∴四边形AEPH、四边形HPFD、四边形BEPG、四边形PFCG是平行四边形,
∴AH=BG=PE,AE=HP=DF,BE=PG=CF,DH=PF=CG,
∵四边形ABCD是菱形,
∴∠EBP=∠GBP,∵PE∥BG,
∴∠EPB=∠GBP,∴∠EBP=∠EPB,
∴BE=PE,∴AH=PE=BG=BE=CF=PG,
同理AE=HP=DF=PF=CG,
∴四边形AEPH的周长=四边形GPFC的周长,∴④正确;
22.【答案】(1)证明 ∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
在Rt△ABE和Rt△ADF中,
∴Rt△ADF≌Rt△ABE(HL)
∴BE=DF,
∵BC=DC,
∴CE=CF;
(2)解 四边形AEMF是菱形,理由:
∵四边形ABCD是正方形,
∴∠BCA=∠DCA=45°,
在△COE和△COF中,
∴△COE≌△COF(SAS),
∴OE=OF,又OM=OA,
∴四边形AEMF是平行四边形,
∵AE=AF,
∴平行四边形AEMF是菱形.
【解析】(1)求简单的线段相等,可证线段所在的三角形全等,即证△ABE≌△ADF;
(2)由于四边形ABCD是正方形,易得∠ECO=∠FCO=45°,BC=CD;联立(1)的结论,可证得EC=CF,根据等腰三角形三线合一的性质可证得OC(即AM)垂直平分EF;已知OA=OM,则EF、AM互相平分,再根据一组邻边相等的平行四边形是菱形,即可判定四边形AEMF是菱形.
23.【答案】证明 ∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
∴△ABE≌△CDF(AAS),
∴AE=CF.
【解析】根据平行四边形的性质得出AB=CD,AB∥CD,根据平行线的性质得出∠ABE=∠CDF,求出∠AEB=∠CFD=90°,根据AAS推出△ABE≌△CDF,得出对应边相等即可.
24.【答案】证明 (1)由平行四边形ABCD,得AD∥BC,AD=BC,∠ADF=∠CBE,
∵AM=CN,
∴AD-AM=BC-CN,
即DM=BN,
又∵DF=BE,
∴△DMF≌△BNE,
∴∠DFM=∠BEN;
(2)由△DMF≌△BNE,得NE=MF,
∵∠DFM=∠BEN,∴∠FEN=∠MFE,
∴MF∥NE,
∴四边形NEMF是平行四边形.
【解析】(1)由平行四边形的性质得到得AD∥BC,AD=BC,∠ADF=∠CBE,然后根据AM=CN得到DM=BN,从而证得△DMF≌△BNE,理由全等三角形对应角相等证得结论;
(2)利用一组对边平行且相等的四边形为平行四边形进行判定即可.
