沪教版(上海)数学八年级第二学期20.4 一次函数的应用(面积问题) 课件(17张PPT)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期20.4 一次函数的应用(面积问题) 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览

文档简介
(共17张PPT)
一次函数的应用
(面积问题)
一 知识点回顾
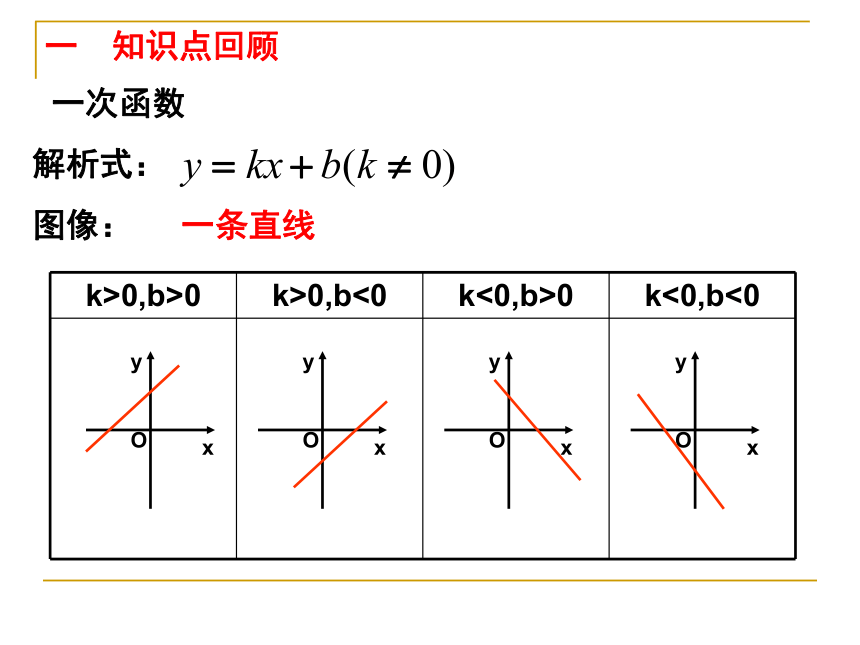
一次函数
解析式:
图像:
一条直线
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
O
x
y
O
x
y
O
x
y
O
x
y
一 知识点回顾
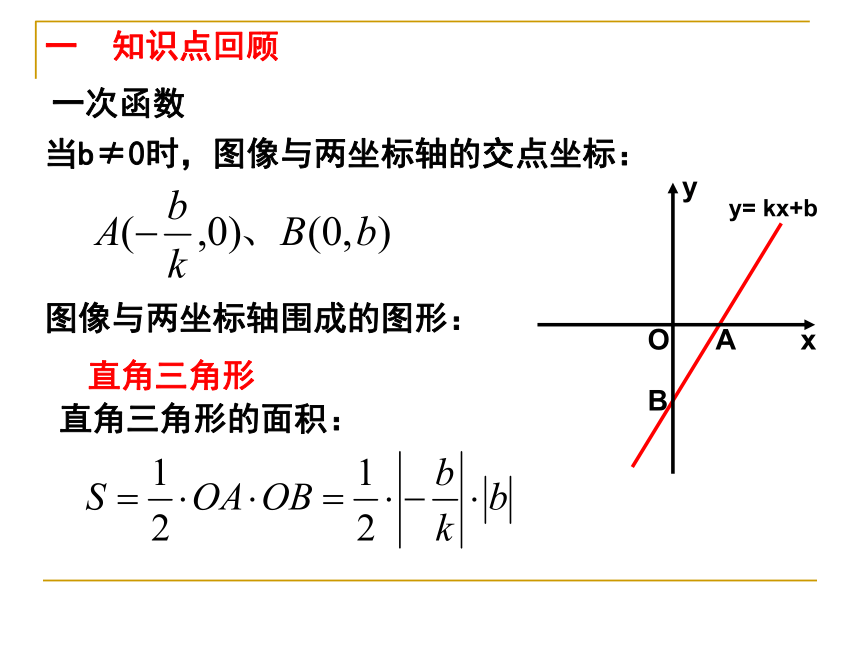
一次函数
当b≠0时,图像与两坐标轴的交点坐标:
图像与两坐标轴围成的图形:
直角三角形
直角三角形的面积:
A
B
O
y=
kx+b
x
y
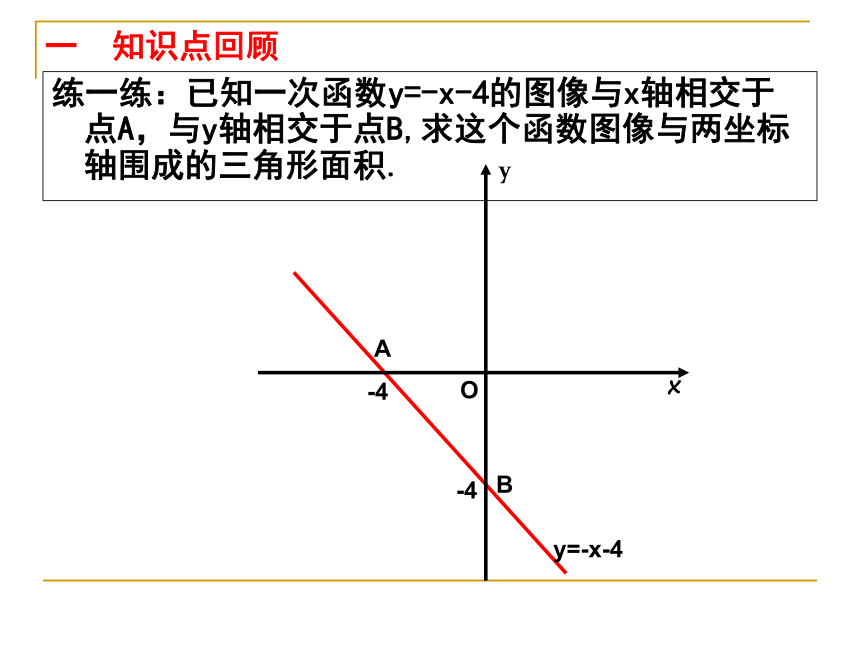
练一练:已知一次函数y=-x-4的图像与x轴相交于点A,与y轴相交于点B,求这个函数图像与两坐标轴围成的三角形面积.
A
B
y=-x-4
-4
-4
x
y
O
一 知识点回顾
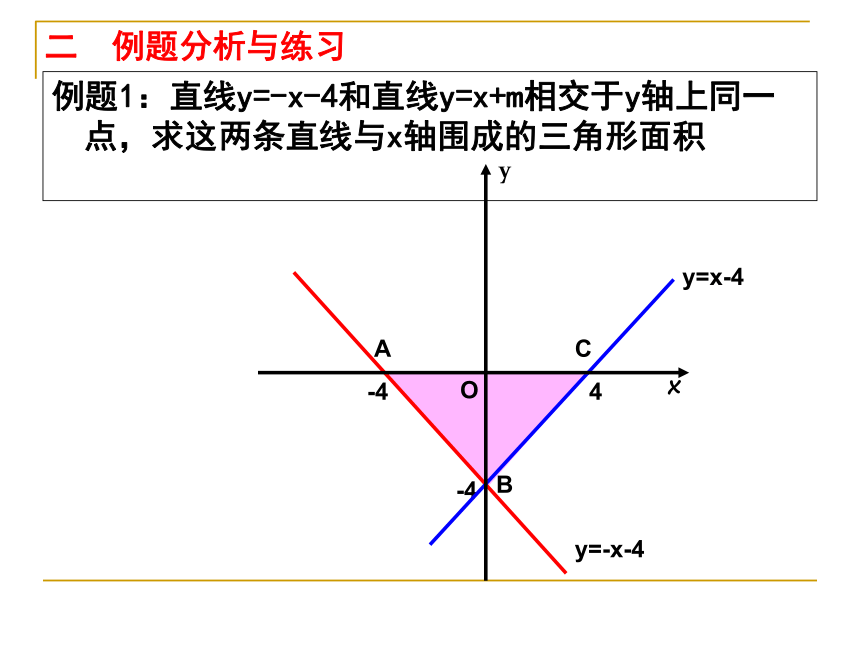
例题1:直线y=-x-4和直线y=x+m相交于y轴上同一点,求这两条直线与x轴围成的三角形面积
二 例题分析与练习
A
B
-4
-4
y=x-4
4
C
x
y
O
y=-x-4
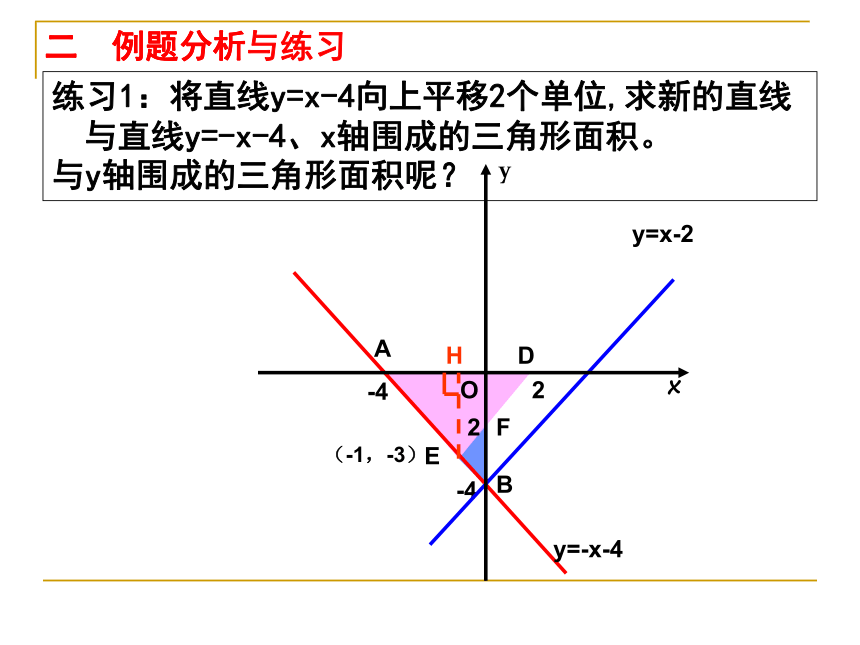
练习1:将直线y=x-4向上平移2个单位,求新的直线与直线y=-x-4、x轴围成的三角形面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
与y轴围成的三角形面积呢?
2
H
二 例题分析与练习
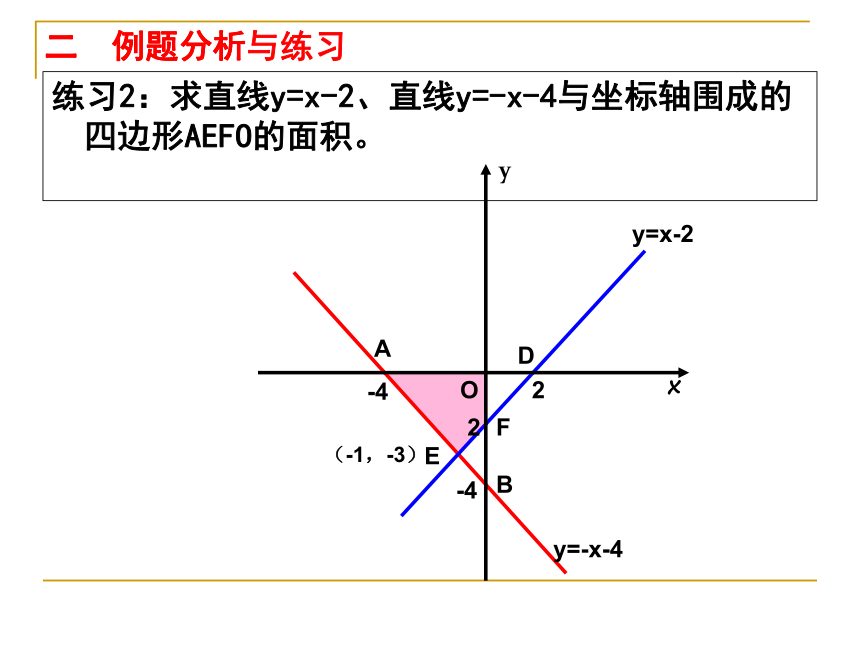
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
例题2:已知一次函数y=kx-4的图像与两坐标轴围成的三角形面积等于8,求一次函数的解析式
二 例题分析
A
B
-4
x
y
O
二 例题分析与练习
练习3:已知直线y=-x+b与坐标轴围成的三角形面积等于8,求该直线的表达式
二 例题分析与练习
A
B
x
y
O
练习4:直线y=-x-4与x轴相交于点A,直线y=kx+b与x轴相交于点D,两条直线相交于点E(-1,-3),△ADE的面积为9,求直线y=kx+b的表达式
二 例题分析
A
B
y=-x-4
-4
-4
E
D
D’
x
y
O
(-1,-3)
H
例题3:已知:一次函数y=-x-4与x轴相交于点A,P是y=-x-4图像上一点,且△AOP的面积等于6,求P点的坐标
P
三
拓展提高
P’
x
y
O
A
-4
H
拓展:直线y=-x-4、直线y=x-2分别与x轴相交于A、B两点,两条直线相交于点C,在直线AC上能否找到点P,使得S△BPC=12,若能,请求出点P的坐标,若不能请说明理由。
P
A
B
C
P’
x
y
O
-4
(-1,-3)
2
四、小结
今天你学会了什么?
请畅所欲言。。。
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
一次函数的应用
(面积问题)
一 知识点回顾
一次函数
解析式:
图像:
一条直线
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
O
x
y
O
x
y
O
x
y
O
x
y
一 知识点回顾
一次函数
当b≠0时,图像与两坐标轴的交点坐标:
图像与两坐标轴围成的图形:
直角三角形
直角三角形的面积:
A
B
O
y=
kx+b
x
y
练一练:已知一次函数y=-x-4的图像与x轴相交于点A,与y轴相交于点B,求这个函数图像与两坐标轴围成的三角形面积.
A
B
y=-x-4
-4
-4
x
y
O
一 知识点回顾
例题1:直线y=-x-4和直线y=x+m相交于y轴上同一点,求这两条直线与x轴围成的三角形面积
二 例题分析与练习
A
B
-4
-4
y=x-4
4
C
x
y
O
y=-x-4
练习1:将直线y=x-4向上平移2个单位,求新的直线与直线y=-x-4、x轴围成的三角形面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
与y轴围成的三角形面积呢?
2
H
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
例题2:已知一次函数y=kx-4的图像与两坐标轴围成的三角形面积等于8,求一次函数的解析式
二 例题分析
A
B
-4
x
y
O
二 例题分析与练习
练习3:已知直线y=-x+b与坐标轴围成的三角形面积等于8,求该直线的表达式
二 例题分析与练习
A
B
x
y
O
练习4:直线y=-x-4与x轴相交于点A,直线y=kx+b与x轴相交于点D,两条直线相交于点E(-1,-3),△ADE的面积为9,求直线y=kx+b的表达式
二 例题分析
A
B
y=-x-4
-4
-4
E
D
D’
x
y
O
(-1,-3)
H
例题3:已知:一次函数y=-x-4与x轴相交于点A,P是y=-x-4图像上一点,且△AOP的面积等于6,求P点的坐标
P
三
拓展提高
P’
x
y
O
A
-4
H
拓展:直线y=-x-4、直线y=x-2分别与x轴相交于A、B两点,两条直线相交于点C,在直线AC上能否找到点P,使得S△BPC=12,若能,请求出点P的坐标,若不能请说明理由。
P
A
B
C
P’
x
y
O
-4
(-1,-3)
2
四、小结
今天你学会了什么?
请畅所欲言。。。
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
练习2:求直线y=x-2、直线y=-x-4与坐标轴围成的四边形AEFO的面积。
二 例题分析
A
B
y=-x-4
-4
-4
y=x-2
D
E
F
x
y
O
(-1,-3)
2
2
二 例题分析与练习
