人教版七年级下册数学第五章相交线与平行线综合复习课件(33张)
文档属性
| 名称 | 人教版七年级下册数学第五章相交线与平行线综合复习课件(33张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览





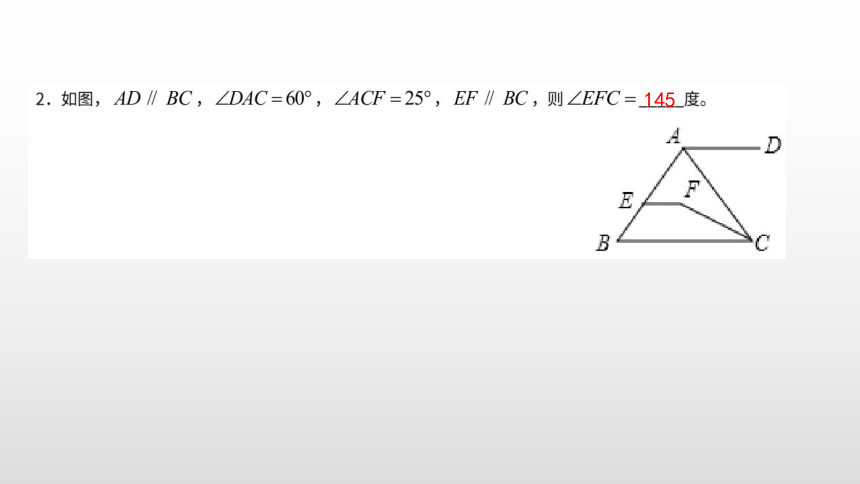
文档简介
(共33张PPT)
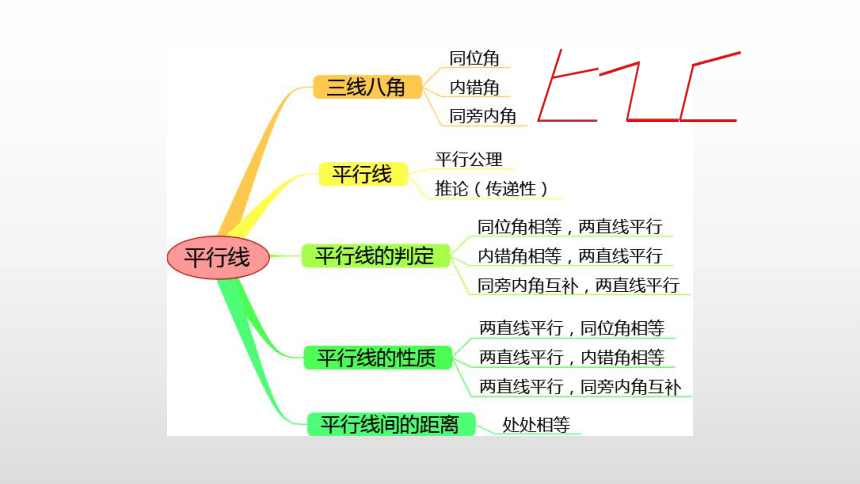
相交线与平行线综合复习
B
A
C
在同一平面内,垂直于同一
条直线的两条直线互相平行。
平行线具有传递性
C
D
B
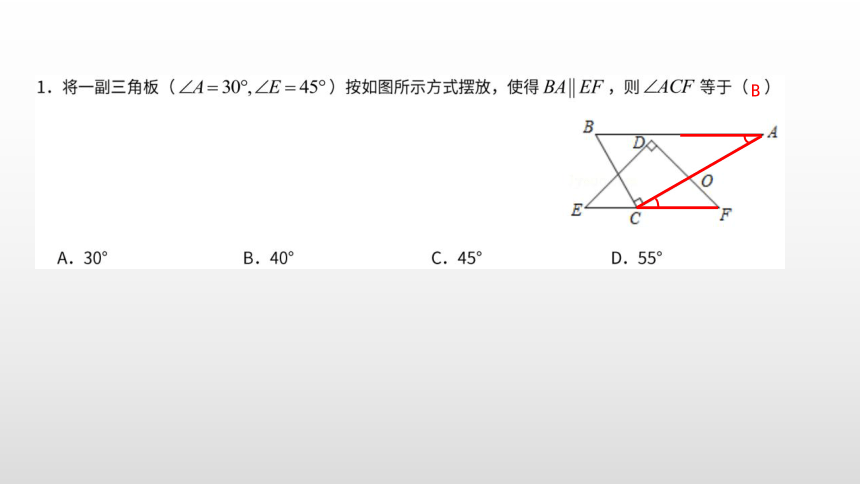
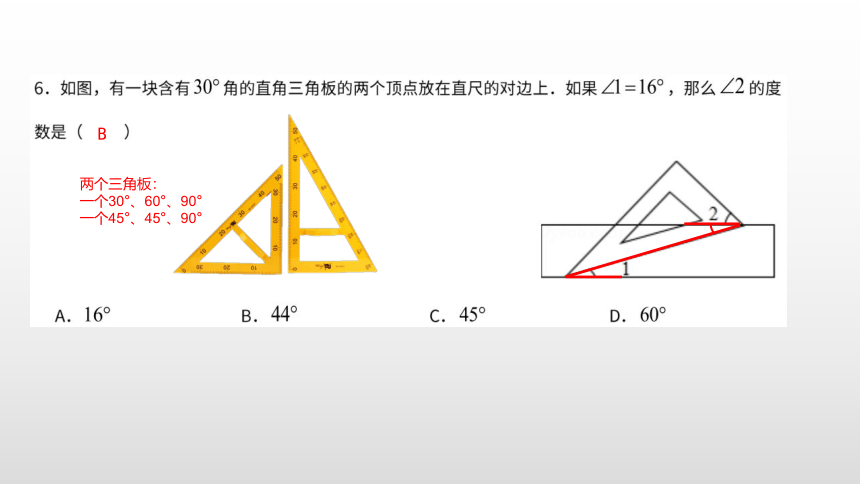
两个三角板:
一个30°、60°、90°
一个45°、45°、90°
C
90
C
145
解:
∵AD∥BC(已知)
∴∠EAD=∠AEB(两直线平行,内错角相等),
∠B+∠BAD=180°(两直线平行,同旁内角互补)
∵∠C=∠EAD(已知)
∴∠C=∠AEB(等量代换)
∴AE∥CD(同位角相等,两直线平行)
∴∠AEF=∠EFC=50°(两直线平行,内错角相等)
∴∠AEB+∠FEC=180°-∠AEF=130°(平角的定义)
∴∠BAD=∠EAD+∠BAE
=∠AEB+∠FEC
=130°(等量代换)
∴∠B=180°-∠BAD=50°(等式的性质)
证明:
∵∠1+∠2=180°(已知)
∠1+∠DFE=180°(邻补角互补)
∴∠2=∠
∠DFE(等量代换)
∴AB∥EF(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
∵∠3=∠B(已知)
∴∠B=∠ADE(等量代换)
∴DE∥BC(同位角相等,两直线平行)
证明:
∵AB∥CD(已知)
∴∠4=∠BAE(两直线平行,同位角相等)
∵∠3=∠4(已知)
∴∠3=∠BAE(等量代换)
∵∠1=∠2(已知)
∴∠CAE+∠1=∠CAE+∠2(等式的性质)
即∠BAE=∠DAC
∴∠3=∠DAC(等量代换)
∴AD∥BE(内错角相等,两直线平行)
证明:
∵∠A=∠1(已知)
∴AC
∥DG(内错角相等,两直线平行)
∴∠C
=∠G(两直线平行,内错角相等)
∵∠C=∠F(已知)
∴∠F
=∠G(等量代换)
∴CG
∥FE(内错角相等,两直线平行)
∴∠CBD
=∠FEH(两直线平行,同位角相等)
∵BM平分∠CBD,EN平分∠FEH(已知)
∴∠2=∠CBD,∠3=
∠FEH
(角平分线的性质)
∴∠2=∠3(等式的性质)
12
A
136°
解:∵AD∥BC(已知)
∴∠A+∠B=180°,
∴∠B=180°-∠A=65°
∠C=180°-∠D=70°
∴∠C+∠D=180°(两直线平行,同旁内角互补)
解:(1)∵CB∥OA,∠B=108°
∴∠AOB=180°-∠B=72°,
∵OE平分∠BOF,∠FOC=∠AOC,
∴∠EOF=∠BOF,∠FOC=
∠AOF,
∴∠EOC=∠EOF+
∠FOC
=∠BOF+∠AOF
=
=36°
解:(2)不变,这个比值是理由如下:
∵CB∥OA
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠AOC=∠AOF,
∴∠OCB:∠OFB=∠AOC:∠AOF=
解:(3)存在,理由如下:
设∠AOC=x,
∵CB∥OA
∴∠OEB=∠AOE=36°+
x,
∠OCB=∠AOC=
x,
∠ACB=180°-∠A=72°
∴∠OCA=∠ACB-∠OCB=72°-
x,
∵∠OEB=∠OCA
∴72°-
x=
36°+
x
,
解得x
=18°,
∴∠OCA=72°-
x=54°
解:(1)证明:
AB∥CD
∠BEF=∠CFE
平分
∠NFE=
∠BEF,∠MEF=
∠CFE
∠NFE=∠MEF
EM∥FN
解:(2)
AB∥CD
∠BEF+∠DFE=180°
平分
∠GFE=
∠DFE,∠GEF=
∠CFE
∠GFE+∠GEF=90°
∠EGF=180°-
(∠GFE+∠GEF)=90°
Q
方法②:
过点G作GQ∥AB,则AB∥GQ∥CD
方法①
R
T
(3)∠G=2∠H。证明如下:
过点G,H作GR∥AB,TH∥AB,则AB∥GR∥TH
∥CD
∵GR∥AB∥CD
∴∠BEG=∠EGR,∠DFG=∠FGR,
∵EH,FH分别平分∠BEG和∠DFG,
∴∠EGF=∠BEG+∠DFG
∴∠BEH=∠BEG,∠DFH=
∠DFG,
∵HT∥AB∥CD
∴∠BEH=∠EHT,∠DFH=∠FHT,
∴∠EHF=
∠BEH
+
∠FHT,
∴∠EHF=
∠BEH
+
∠FHT
=
∠BEG+
∠DFG
=
∠EGF
,
即∠G=2∠H.
同理可得:∠G
=
2∠H
=
4∠I.
解:(1)证明:
过点E作EF∥AB,则AB∥EF∥CD,
H
证明:延长FG2交AB于点H
方法①
∵FH平分角EFD
∴∠EFH=∠DFH
∵AB∥CD
∴∠DFH=∠AHF
∴∠EFH=∠AHF
∴∠EG2H=180°-∠1-∠AHF
=180°-∠2-∠EFH
=∠FG1E
∴∠FG1E+∠EG2G1=∠EG2H+
∠EG2G1=180°
方法②
证明:过点G1作G1P∥AB,过点G2作G2Q∥AB
由(1)的结论可知:
∠FG1E=∠3+∠1+∠4
∠FG2E=∠1+∠3
∴∠FG1E+∠EG2G1
=
∠3+∠1+∠4+
∠1+∠3
=
2∠3+(∠1+∠2+∠4)
=∠EFD+∠FEB
=180°
P
Q
3
4
相交线与平行线综合复习
B
A
C
在同一平面内,垂直于同一
条直线的两条直线互相平行。
平行线具有传递性
C
D
B
两个三角板:
一个30°、60°、90°
一个45°、45°、90°
C
90
C
145
解:
∵AD∥BC(已知)
∴∠EAD=∠AEB(两直线平行,内错角相等),
∠B+∠BAD=180°(两直线平行,同旁内角互补)
∵∠C=∠EAD(已知)
∴∠C=∠AEB(等量代换)
∴AE∥CD(同位角相等,两直线平行)
∴∠AEF=∠EFC=50°(两直线平行,内错角相等)
∴∠AEB+∠FEC=180°-∠AEF=130°(平角的定义)
∴∠BAD=∠EAD+∠BAE
=∠AEB+∠FEC
=130°(等量代换)
∴∠B=180°-∠BAD=50°(等式的性质)
证明:
∵∠1+∠2=180°(已知)
∠1+∠DFE=180°(邻补角互补)
∴∠2=∠
∠DFE(等量代换)
∴AB∥EF(内错角相等,两直线平行)
∴∠3=∠ADE(两直线平行,内错角相等)
∵∠3=∠B(已知)
∴∠B=∠ADE(等量代换)
∴DE∥BC(同位角相等,两直线平行)
证明:
∵AB∥CD(已知)
∴∠4=∠BAE(两直线平行,同位角相等)
∵∠3=∠4(已知)
∴∠3=∠BAE(等量代换)
∵∠1=∠2(已知)
∴∠CAE+∠1=∠CAE+∠2(等式的性质)
即∠BAE=∠DAC
∴∠3=∠DAC(等量代换)
∴AD∥BE(内错角相等,两直线平行)
证明:
∵∠A=∠1(已知)
∴AC
∥DG(内错角相等,两直线平行)
∴∠C
=∠G(两直线平行,内错角相等)
∵∠C=∠F(已知)
∴∠F
=∠G(等量代换)
∴CG
∥FE(内错角相等,两直线平行)
∴∠CBD
=∠FEH(两直线平行,同位角相等)
∵BM平分∠CBD,EN平分∠FEH(已知)
∴∠2=∠CBD,∠3=
∠FEH
(角平分线的性质)
∴∠2=∠3(等式的性质)
12
A
136°
解:∵AD∥BC(已知)
∴∠A+∠B=180°,
∴∠B=180°-∠A=65°
∠C=180°-∠D=70°
∴∠C+∠D=180°(两直线平行,同旁内角互补)
解:(1)∵CB∥OA,∠B=108°
∴∠AOB=180°-∠B=72°,
∵OE平分∠BOF,∠FOC=∠AOC,
∴∠EOF=∠BOF,∠FOC=
∠AOF,
∴∠EOC=∠EOF+
∠FOC
=∠BOF+∠AOF
=
=36°
解:(2)不变,这个比值是理由如下:
∵CB∥OA
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠AOC=∠AOF,
∴∠OCB:∠OFB=∠AOC:∠AOF=
解:(3)存在,理由如下:
设∠AOC=x,
∵CB∥OA
∴∠OEB=∠AOE=36°+
x,
∠OCB=∠AOC=
x,
∠ACB=180°-∠A=72°
∴∠OCA=∠ACB-∠OCB=72°-
x,
∵∠OEB=∠OCA
∴72°-
x=
36°+
x
,
解得x
=18°,
∴∠OCA=72°-
x=54°
解:(1)证明:
AB∥CD
∠BEF=∠CFE
平分
∠NFE=
∠BEF,∠MEF=
∠CFE
∠NFE=∠MEF
EM∥FN
解:(2)
AB∥CD
∠BEF+∠DFE=180°
平分
∠GFE=
∠DFE,∠GEF=
∠CFE
∠GFE+∠GEF=90°
∠EGF=180°-
(∠GFE+∠GEF)=90°
Q
方法②:
过点G作GQ∥AB,则AB∥GQ∥CD
方法①
R
T
(3)∠G=2∠H。证明如下:
过点G,H作GR∥AB,TH∥AB,则AB∥GR∥TH
∥CD
∵GR∥AB∥CD
∴∠BEG=∠EGR,∠DFG=∠FGR,
∵EH,FH分别平分∠BEG和∠DFG,
∴∠EGF=∠BEG+∠DFG
∴∠BEH=∠BEG,∠DFH=
∠DFG,
∵HT∥AB∥CD
∴∠BEH=∠EHT,∠DFH=∠FHT,
∴∠EHF=
∠BEH
+
∠FHT,
∴∠EHF=
∠BEH
+
∠FHT
=
∠BEG+
∠DFG
=
∠EGF
,
即∠G=2∠H.
同理可得:∠G
=
2∠H
=
4∠I.
解:(1)证明:
过点E作EF∥AB,则AB∥EF∥CD,
H
证明:延长FG2交AB于点H
方法①
∵FH平分角EFD
∴∠EFH=∠DFH
∵AB∥CD
∴∠DFH=∠AHF
∴∠EFH=∠AHF
∴∠EG2H=180°-∠1-∠AHF
=180°-∠2-∠EFH
=∠FG1E
∴∠FG1E+∠EG2G1=∠EG2H+
∠EG2G1=180°
方法②
证明:过点G1作G1P∥AB,过点G2作G2Q∥AB
由(1)的结论可知:
∠FG1E=∠3+∠1+∠4
∠FG2E=∠1+∠3
∴∠FG1E+∠EG2G1
=
∠3+∠1+∠4+
∠1+∠3
=
2∠3+(∠1+∠2+∠4)
=∠EFD+∠FEB
=180°
P
Q
3
4
