六年级数学下册课件 - 6.4正比例和反比例练习 -苏教版(共29张PPT))
文档属性
| 名称 | 六年级数学下册课件 - 6.4正比例和反比例练习 -苏教版(共29张PPT)) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
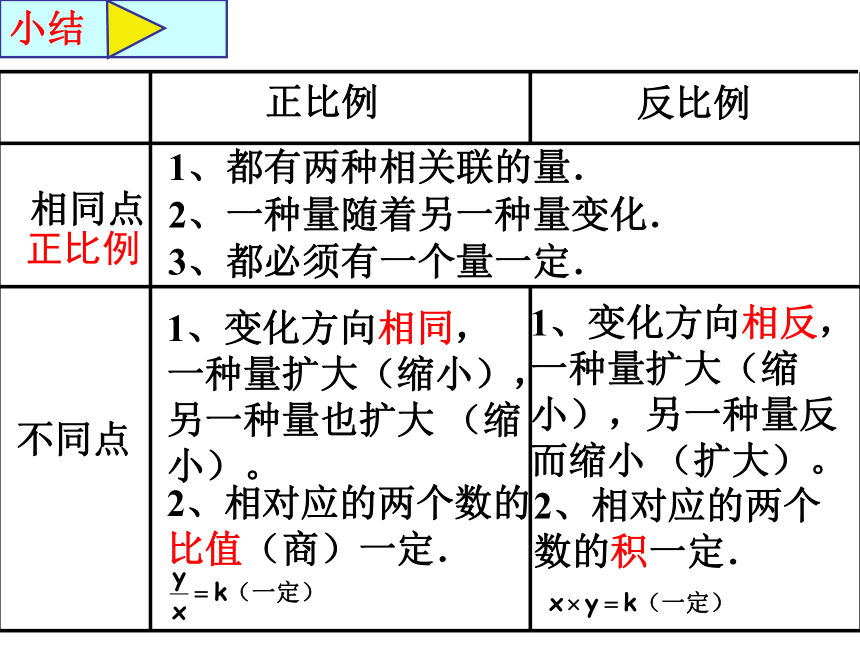
小结
正比例
反比例
相同点
不同点
1、都有两种相关联的量.
2、一种量随着另一种量变化.
1、变化方向相同,
一种量扩大(缩小),另一种量也扩大
(缩小)。
1、变化方向相反,一种量扩大(缩小),另一种量反而缩小
(扩大)。
2、相对应的两个数的
比值(商)一定.
2、相对应的两个数的积一定.
3、都必须有一个量一定.
正比例
跟我学技巧:
正比反比两同胞,
“关联”相同要记牢。
比值一定成正比,
乘积一定成反比。
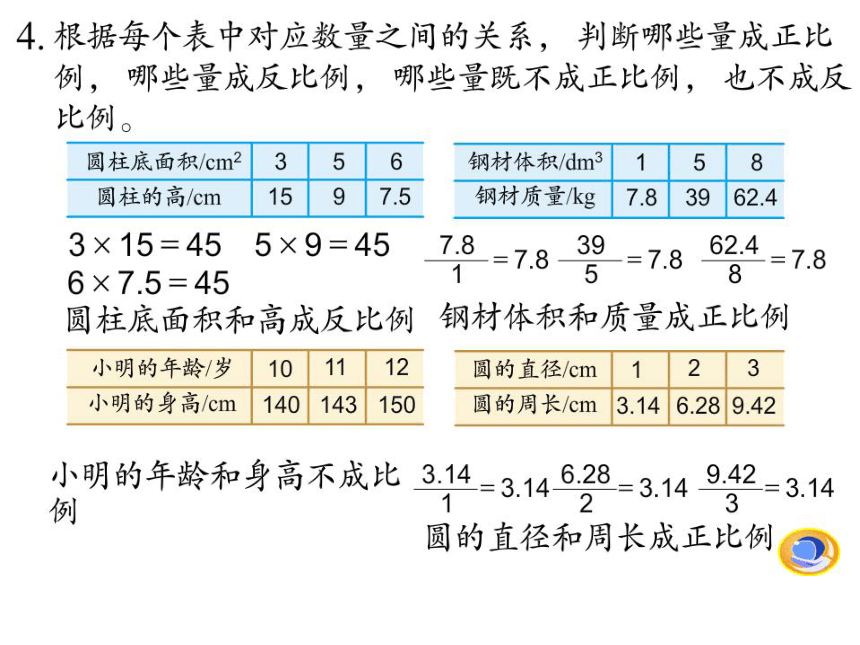
在表1中相关联的量是(
)和(
),(
)随着(
)变化,(
)是一定的。因此,总价和数量成(
)比例关系。
观察下面两张表格,并回答问题:
数量/本
1
3
6
8
总价/元
4
12
24
32
(1)购买同一种笔记本的数量和总价如下表。
数量
总价
正
总价
数量
比值即单价
4︰1=4
12︰3=4
24︰6=4
在表2中相关联的量是(
)和(
),(
)随着(
)变化,(
)是一定的。因此,单价和数量成(
)比例关系。
单价/元
2
3
4
5
数量/本
30
20
15
12
(2)用同样的钱购买不同笔记本的单价和数量如下表。
单价
数量
反
数量
积即总价
30×2=60
20×30=60
15×4=60
单价
=数量(一定)
单价
总价
因为:
所以:笔记本的单价和总价成正比例。
想一想,如果购买笔记本的数量一定,笔记本的单价和总价成什么比例?
实际距离/m
40
80
120
5.下面的图像表示一幅地图图上距离和实际距离的关系
160
200
240
280
0
1
3
4
5
2
6
7
8
图上距离/cm
?
?
?
?
?
?
?
(1)看图填写下表。
图上距离/cm
1
2
3
4
5
6
7
……
实际距离/m
……
40
80
120
160
200
240
280
(2)根据上面的图像,你能说出这幅地图的比例尺是多少吗?图上距离和实际距离成什么比例?为什么?
答
:从图像上可看出这幅地图的比例尺是1
:4000。图上距离和实际距离成正比例。因为图上距离
:实际距离=比例尺(一定)
(3)在这幅地图上,量得甲乙两地的图上距离是12厘米,两地的实际距离是多少米?
40×12=480(米)
答:两地的实际距离是480米。
1厘米
:40米=1
:4000
6.四名同学都看了《我们爱科学》这本书。(1)填写每人看完这本书需要的天数。
每天看的页数和需要看的天数成什么比例?
(2)照这样的速度看了3天,他们各看了多少页,还剩多少页?把结果填在表中。
已看的页数和剩下的页数成比例吗?为什么?
?
王明
新
李
虹
张之
华
郑
强
每天看页数
20
15
10
6
需要看天数
9
?
?
?
?
王明新
李
虹
张之
华
郑
强
已看的页数
?
?
?
?
剩下的页数
?
?
?
?
12
120
60
30
18
答:每天看的页数和需要的天数成反比例。因为每天看的页数×需要看的页数=总页数(一定)
45
答:已看的页数和剩下的页数不成比例。因为已看页数与剩下页数是和一定,不是积一定,也不是比值一定。
162
18
150
30
135
(1)120名同学参加团体操表演,每排的人数和排数。
(2)小军每分钟浇树的棵树一定,浇树的时间和浇树的总棵树。
(3)用同样大的正方形地砖铺地,地砖的块数和铺地的面积。
(4)一个商场每天的营业时间一定,每天接待顾客的数量与营业额。
(5)购买商品的总价一定,商品的单价和数量。
成反比例
成正比例
成正比例
不成正比例,也不成反比例。
成反比例。
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
思考
路程、速度和时间这三个量中每两个量之间有什么样的比例关系?
当路程一定时,速度和时间成
当速度一定时,路程和时间成
当时间一定时,路程和速度成
反比例关系
正比例关系
正比例关系
速度×时间=路程(一定)
=速度(一定)
时间
路程
=时间(一定)
速度
路程
做一做
判断工效、时间和总量中一种量一定,另外两种量成什么比例关系。为什么?
工效一定,时间和工作总量
。
工作总量一定,工效和时间
。
时间一定,工作总量和工效
。
成正比例
成反比例
成正比例
=工效(一定)
时间
总量
工效×时间=工作总量(一定)
=时间(一定)
工效
总量
易错易混题(一)
1、瓷砖面积一定,
砖的块数和铺地面积。
铺地面积÷砖的块数=
每块瓷砖的面积(一定)
正比例
2、铺地面积一定,每块砖的面积和所需块数。
每块砖的面积×所需块数=铺地的面积。(一定)
反比例
易错易混题(一)
3、铺地面积一定,每块砖的边长和所需块数.
不成比例
易错易混题(一)
1、瓷砖面积一定,
砖的块数和铺地面积.
2、铺地面积一定,每块砖的面积和所需块数.
3、铺地面积一定,方砖边长和所需块数.
(正比例)
(不成比例)
(反比例)
易错易混题(一)
1、生产总时间一定,生产一个零件的时间和个数
2、生产一个零件时间一定,生产零件的总时间和个数
(反比例)
(正比例)
易错易混题(二)
1
圆的周长和半径。
2
圆的周长一定,圆周率和直径。
3
圆的面积和半径的平方。
(正比例)
(正比例)
(不成比例)
易错易混题(三)
4
正方形的面积和边长。
5
正方体的体积和它的棱长。
6
正方体一个面的面积和它的表面积。
(不成比例)
(不成比例)
(正比例)
易错易混题(三)
3、铺地面积一定,方砖边长和所需块数.
不成比例
易错易混题(一)
下表中x和y是两种相关联的量观察规律,请把表格填写完整。
X
0.5
0.6
1
y
1.5
2.7
3
1.8
0.9
χ
3
4
y
=
(2)若
,
(χ,y均不为0)则χ和y,成(
)比例.
若χ和y是两种相关联的量,判断它们是否成比例,成什么比例?
(1)若5χ=
4y,(χ,y均不为0)
则χ和y成(
)比例.
正
正
(4)若x
=
y+5,则x和y(
)比例
=y(K一定),
则x和y成(
)比例
K+3
X
(5)若
不成
反
X
3
=
4
y
(3)若
,则x和y成(
)比例
反
汽车的速度是火车速度的
,两车从A地同时向B地开出,火车6小时到达,当火车到达B地时,汽车还需要再行(
)小时.
3
4
2
已知AE=ED,BC=3BD,
△ABC=30
c㎡,求阴影部分面积
S
A
B
C
D
E
F
1
2
1
1
小结
正比例
反比例
相同点
不同点
1、都有两种相关联的量.
2、一种量随着另一种量变化.
1、变化方向相同,
一种量扩大(缩小),另一种量也扩大
(缩小)。
1、变化方向相反,一种量扩大(缩小),另一种量反而缩小
(扩大)。
2、相对应的两个数的
比值(商)一定.
2、相对应的两个数的积一定.
3、都必须有一个量一定.
正比例
跟我学技巧:
正比反比两同胞,
“关联”相同要记牢。
比值一定成正比,
乘积一定成反比。
在表1中相关联的量是(
)和(
),(
)随着(
)变化,(
)是一定的。因此,总价和数量成(
)比例关系。
观察下面两张表格,并回答问题:
数量/本
1
3
6
8
总价/元
4
12
24
32
(1)购买同一种笔记本的数量和总价如下表。
数量
总价
正
总价
数量
比值即单价
4︰1=4
12︰3=4
24︰6=4
在表2中相关联的量是(
)和(
),(
)随着(
)变化,(
)是一定的。因此,单价和数量成(
)比例关系。
单价/元
2
3
4
5
数量/本
30
20
15
12
(2)用同样的钱购买不同笔记本的单价和数量如下表。
单价
数量
反
数量
积即总价
30×2=60
20×30=60
15×4=60
单价
=数量(一定)
单价
总价
因为:
所以:笔记本的单价和总价成正比例。
想一想,如果购买笔记本的数量一定,笔记本的单价和总价成什么比例?
实际距离/m
40
80
120
5.下面的图像表示一幅地图图上距离和实际距离的关系
160
200
240
280
0
1
3
4
5
2
6
7
8
图上距离/cm
?
?
?
?
?
?
?
(1)看图填写下表。
图上距离/cm
1
2
3
4
5
6
7
……
实际距离/m
……
40
80
120
160
200
240
280
(2)根据上面的图像,你能说出这幅地图的比例尺是多少吗?图上距离和实际距离成什么比例?为什么?
答
:从图像上可看出这幅地图的比例尺是1
:4000。图上距离和实际距离成正比例。因为图上距离
:实际距离=比例尺(一定)
(3)在这幅地图上,量得甲乙两地的图上距离是12厘米,两地的实际距离是多少米?
40×12=480(米)
答:两地的实际距离是480米。
1厘米
:40米=1
:4000
6.四名同学都看了《我们爱科学》这本书。(1)填写每人看完这本书需要的天数。
每天看的页数和需要看的天数成什么比例?
(2)照这样的速度看了3天,他们各看了多少页,还剩多少页?把结果填在表中。
已看的页数和剩下的页数成比例吗?为什么?
?
王明
新
李
虹
张之
华
郑
强
每天看页数
20
15
10
6
需要看天数
9
?
?
?
?
王明新
李
虹
张之
华
郑
强
已看的页数
?
?
?
?
剩下的页数
?
?
?
?
12
120
60
30
18
答:每天看的页数和需要的天数成反比例。因为每天看的页数×需要看的页数=总页数(一定)
45
答:已看的页数和剩下的页数不成比例。因为已看页数与剩下页数是和一定,不是积一定,也不是比值一定。
162
18
150
30
135
(1)120名同学参加团体操表演,每排的人数和排数。
(2)小军每分钟浇树的棵树一定,浇树的时间和浇树的总棵树。
(3)用同样大的正方形地砖铺地,地砖的块数和铺地的面积。
(4)一个商场每天的营业时间一定,每天接待顾客的数量与营业额。
(5)购买商品的总价一定,商品的单价和数量。
成反比例
成正比例
成正比例
不成正比例,也不成反比例。
成反比例。
两种量
不相关联
相关联
加的关系
减的关系
乘的关系
除的关系
→不成比例
→不成比例
→不成比例
积一定
商一定
→成反比例
→成正比例
思考
路程、速度和时间这三个量中每两个量之间有什么样的比例关系?
当路程一定时,速度和时间成
当速度一定时,路程和时间成
当时间一定时,路程和速度成
反比例关系
正比例关系
正比例关系
速度×时间=路程(一定)
=速度(一定)
时间
路程
=时间(一定)
速度
路程
做一做
判断工效、时间和总量中一种量一定,另外两种量成什么比例关系。为什么?
工效一定,时间和工作总量
。
工作总量一定,工效和时间
。
时间一定,工作总量和工效
。
成正比例
成反比例
成正比例
=工效(一定)
时间
总量
工效×时间=工作总量(一定)
=时间(一定)
工效
总量
易错易混题(一)
1、瓷砖面积一定,
砖的块数和铺地面积。
铺地面积÷砖的块数=
每块瓷砖的面积(一定)
正比例
2、铺地面积一定,每块砖的面积和所需块数。
每块砖的面积×所需块数=铺地的面积。(一定)
反比例
易错易混题(一)
3、铺地面积一定,每块砖的边长和所需块数.
不成比例
易错易混题(一)
1、瓷砖面积一定,
砖的块数和铺地面积.
2、铺地面积一定,每块砖的面积和所需块数.
3、铺地面积一定,方砖边长和所需块数.
(正比例)
(不成比例)
(反比例)
易错易混题(一)
1、生产总时间一定,生产一个零件的时间和个数
2、生产一个零件时间一定,生产零件的总时间和个数
(反比例)
(正比例)
易错易混题(二)
1
圆的周长和半径。
2
圆的周长一定,圆周率和直径。
3
圆的面积和半径的平方。
(正比例)
(正比例)
(不成比例)
易错易混题(三)
4
正方形的面积和边长。
5
正方体的体积和它的棱长。
6
正方体一个面的面积和它的表面积。
(不成比例)
(不成比例)
(正比例)
易错易混题(三)
3、铺地面积一定,方砖边长和所需块数.
不成比例
易错易混题(一)
下表中x和y是两种相关联的量观察规律,请把表格填写完整。
X
0.5
0.6
1
y
1.5
2.7
3
1.8
0.9
χ
3
4
y
=
(2)若
,
(χ,y均不为0)则χ和y,成(
)比例.
若χ和y是两种相关联的量,判断它们是否成比例,成什么比例?
(1)若5χ=
4y,(χ,y均不为0)
则χ和y成(
)比例.
正
正
(4)若x
=
y+5,则x和y(
)比例
=y(K一定),
则x和y成(
)比例
K+3
X
(5)若
不成
反
X
3
=
4
y
(3)若
,则x和y成(
)比例
反
汽车的速度是火车速度的
,两车从A地同时向B地开出,火车6小时到达,当火车到达B地时,汽车还需要再行(
)小时.
3
4
2
已知AE=ED,BC=3BD,
△ABC=30
c㎡,求阴影部分面积
S
A
B
C
D
E
F
1
2
1
1
