8.3 实际问题与二元一次方程组(第二课时) 课件(共16张PPT)
文档属性
| 名称 | 8.3 实际问题与二元一次方程组(第二课时) 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 08:03:59 | ||
图片预览






文档简介
8.3 实际问题与二元一次方程组
第八章 二元一次方程组
2021年春人教版七年级(下)数学
1、知道用二元一次方程组解决实际问题的一般步骤。
2、通过题干信息,找数量关系,列方程并求解。
会用列方程组的方法解决实际问题。(重点)
分析题干信息,找数量关系。(难点)
学习目标
利用二元一次方程组解决问题的步骤
用二元一次方程组解决实际问题的步骤:
审:理解并找出实际问题中的等量关系;
设:用代数式表示实际问题中的基础数据;
列:找到所列代数式中的等量关系,以此为依据列出方程;
解:求解;
验:考虑求出的解是否具有实际意义;
答:实际问题的答案.
知识回顾
问题一:要想知道这批产品的销售款比原料费与运输费的和多多少元,我们需要知道哪些量?
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
购买原料量(x吨)
制成成品量(y吨)
运输原料运费
原料费
运输成品运费
销售额
1000x
8000y
铁路运费
公路运费
铁路运费
公路运费
1.5x×10
1.5y×20
1.2x×120
1.2y×110
新课导入
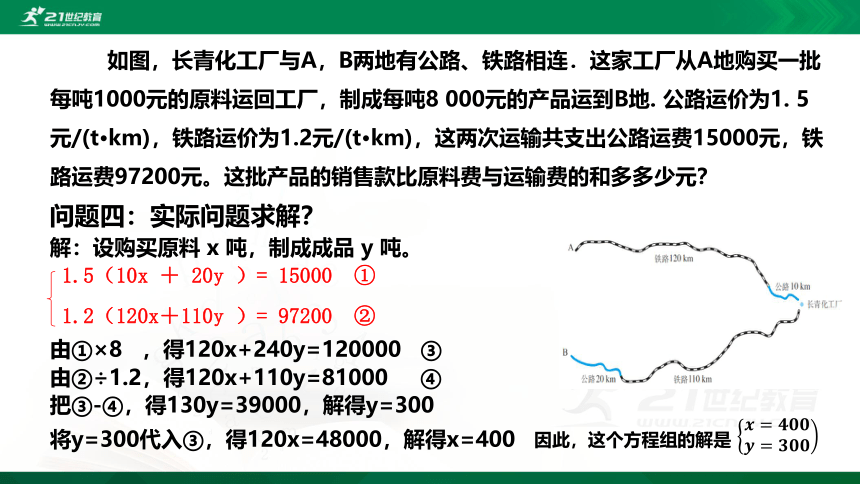
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
问题二:想一想题干中有哪些数量关系?
问题三:根据数量关系列方程,并求出具体数值?
运输原料公路运费+运输成品公路运费=公路运费合计
运输原料铁路运费+运输成品铁路运费=铁路运费合计
解:设购买原料 x 吨,制成成品 y 吨。
1.5(10x + 20y )= 15000 ①
1.2(120x+110y )= 97200 ②
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
问题四:实际问题求解?
由①×8 ,得120x+240y=120000 ③
把③-④,得130y=39000,解得y=300
将y=300代入③,得120x=48000,解得x=400
由②÷1.2,得120x+110y=81000 ④
&????=??????????????&????=??????????????
?
因此,这个方程组的解是
解:设购买原料 x 吨,制成成品 y 吨。
1.5(10x + 20y )= 15000 ①
1.2(120x+110y )= 97200 ②
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
问题四:这批产品的销售款比原料费与运输费的和多多少元?
销售额:8 000×300=2400000元;
原料费:1 000×400=400000元;
运输费:15000+97200=112200元.
这批产品的销售款比原料费与运输费的和多1887800元.
1.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19 B.18 C.16 D.15
【答案】C
【解析】
设笑脸形的气球x元一个,爱心形的气球y元一个,由题意,得{????????+????=????????????+????????=????????,
两式相加,得,4x+4y=32,即2x+2y=16.
故选C.
?
课堂练习
2.利用两块长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
【答案】D
【详解】
设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,
由第一个图形可知桌子的高度为:h-y+x=79,
由第二个图形可知桌子的高度为:h-x+y=73,
两个方程相加得:(h-y+x)+(h-x+y)=152,
解得:h=76cm.故选D.
3.某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年“元旦”期间的销售情况,下面是调查后小明与其它两位同学进行交流的情景.
小明说:“去年两超市销售额共为150万元,今年两超市销售额共为170万元”,
小亮说:“甲超市销售额今年比去年增加10%
小颖说:“乙超市销售额今年比去年增加20%
根据他们的对话,得出今年甲超市销售额为_____万元
【答案】110
【详解】
解:设甲超市去年销售额为x万元,乙超市去年销售额为y万元,
根据题意得
解得
所以今年甲超市销售额为(????+????????%)×????????????=????????????(万元).
?
4.《九章算术》有个题目,大意是:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重.”设每只雀、燕的重量分别为x两,y两,可得方程组是___________.
【分析】
可以设每只雀、燕的重量各为x两,y两,根据总重为16两,互换一只重量相等,列出方程组即可.
【详解】
设每只雀、燕的重量各为x两,y两,由题意得: 5x+6y=16
4x+y=5y+x.
解方程组得:
5.甲、乙两地相距280 km,一轮船在两地间航行,顺流用14 h,逆流用20 h.则这艘轮船在静水中的速度为__________.
【详解】
设轮船在静水的速度为????????????/????,水流速度为????????????/????,
则:轮船顺流速度为:????+????????????/????,逆流速度为:?????????????????/????,
∴ ,解得: ,
∴轮船在静水中速度为????????????????/????,
故答案为:????????????????/????.
?
6.某学校将开启“大阅读”活动,为了充实书吧藏书,学生会号召全年级学生捐书,得到各班的大力支持.同时,年级部分备课组的老师也购买藏书充实到年级书吧,其中数学组购买了甲、乙两种自然科学书籍若干本,用去699元;语文组购买了A、B两种文学书籍若干本,用去6138元,已知A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同,若甲种书的单价比乙种书的单价多7元,则乙种书籍比甲种书籍多买了_____本.
【详解】
解:设乙种书籍的单价为每本????元,则甲种书籍的单价为(????+????)元,A种书籍的单价为每本????元,B种书籍的单价为(????+????)元,设A购买了????本,B购买了????本,则甲购买了????本,乙购买了????本,所以:
?
②-①得:????????+????(????+????)?????(????+????)?????????=????????????????
所以:????(?????????)=????????????????,所以:?????????=????????????.所以:乙比甲多买了????????????本.
?
课堂小结
再见
第八章 二元一次方程组
2021年春人教版七年级(下)数学
1、知道用二元一次方程组解决实际问题的一般步骤。
2、通过题干信息,找数量关系,列方程并求解。
会用列方程组的方法解决实际问题。(重点)
分析题干信息,找数量关系。(难点)
学习目标
利用二元一次方程组解决问题的步骤
用二元一次方程组解决实际问题的步骤:
审:理解并找出实际问题中的等量关系;
设:用代数式表示实际问题中的基础数据;
列:找到所列代数式中的等量关系,以此为依据列出方程;
解:求解;
验:考虑求出的解是否具有实际意义;
答:实际问题的答案.
知识回顾
问题一:要想知道这批产品的销售款比原料费与运输费的和多多少元,我们需要知道哪些量?
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
购买原料量(x吨)
制成成品量(y吨)
运输原料运费
原料费
运输成品运费
销售额
1000x
8000y
铁路运费
公路运费
铁路运费
公路运费
1.5x×10
1.5y×20
1.2x×120
1.2y×110
新课导入
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
问题二:想一想题干中有哪些数量关系?
问题三:根据数量关系列方程,并求出具体数值?
运输原料公路运费+运输成品公路运费=公路运费合计
运输原料铁路运费+运输成品铁路运费=铁路运费合计
解:设购买原料 x 吨,制成成品 y 吨。
1.5(10x + 20y )= 15000 ①
1.2(120x+110y )= 97200 ②
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
问题四:实际问题求解?
由①×8 ,得120x+240y=120000 ③
把③-④,得130y=39000,解得y=300
将y=300代入③,得120x=48000,解得x=400
由②÷1.2,得120x+110y=81000 ④
&????=??????????????&????=??????????????
?
因此,这个方程组的解是
解:设购买原料 x 吨,制成成品 y 吨。
1.5(10x + 20y )= 15000 ①
1.2(120x+110y )= 97200 ②
如图,长青化工厂与A,B两地有公路、铁路相连.这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地. 公路运价为1. 5元/(t·km),铁路运价为1.2元/(t·km),这两次运输共支出公路运费15000元,铁路运费97200元。这批产品的销售款比原料费与运输费的和多多少元?
问题四:这批产品的销售款比原料费与运输费的和多多少元?
销售额:8 000×300=2400000元;
原料费:1 000×400=400000元;
运输费:15000+97200=112200元.
这批产品的销售款比原料费与运输费的和多1887800元.
1.陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )
A.19 B.18 C.16 D.15
【答案】C
【解析】
设笑脸形的气球x元一个,爱心形的气球y元一个,由题意,得{????????+????=????????????+????????=????????,
两式相加,得,4x+4y=32,即2x+2y=16.
故选C.
?
课堂练习
2.利用两块长方体测量一张桌子的高度,首先按图①方式放置,再交换木块的位置,按图②方式放置,测量的数据如图,则桌子的高度是( )
A.73cm B.74cm C.75cm D.76cm
【答案】D
【详解】
设桌子的高度为hcm,第一个长方体的长为xcm,第二个长方体的宽为ycm,
由第一个图形可知桌子的高度为:h-y+x=79,
由第二个图形可知桌子的高度为:h-x+y=73,
两个方程相加得:(h-y+x)+(h-x+y)=152,
解得:h=76cm.故选D.
3.某班的一个综合实践活动小组去甲、乙两个超市调查去年和今年“元旦”期间的销售情况,下面是调查后小明与其它两位同学进行交流的情景.
小明说:“去年两超市销售额共为150万元,今年两超市销售额共为170万元”,
小亮说:“甲超市销售额今年比去年增加10%
小颖说:“乙超市销售额今年比去年增加20%
根据他们的对话,得出今年甲超市销售额为_____万元
【答案】110
【详解】
解:设甲超市去年销售额为x万元,乙超市去年销售额为y万元,
根据题意得
解得
所以今年甲超市销售额为(????+????????%)×????????????=????????????(万元).
?
4.《九章算术》有个题目,大意是:“五只雀、六只燕,共重16两,雀重燕轻,互换其中一只,恰好一样重.”设每只雀、燕的重量分别为x两,y两,可得方程组是___________.
【分析】
可以设每只雀、燕的重量各为x两,y两,根据总重为16两,互换一只重量相等,列出方程组即可.
【详解】
设每只雀、燕的重量各为x两,y两,由题意得: 5x+6y=16
4x+y=5y+x.
解方程组得:
5.甲、乙两地相距280 km,一轮船在两地间航行,顺流用14 h,逆流用20 h.则这艘轮船在静水中的速度为__________.
【详解】
设轮船在静水的速度为????????????/????,水流速度为????????????/????,
则:轮船顺流速度为:????+????????????/????,逆流速度为:?????????????????/????,
∴ ,解得: ,
∴轮船在静水中速度为????????????????/????,
故答案为:????????????????/????.
?
6.某学校将开启“大阅读”活动,为了充实书吧藏书,学生会号召全年级学生捐书,得到各班的大力支持.同时,年级部分备课组的老师也购买藏书充实到年级书吧,其中数学组购买了甲、乙两种自然科学书籍若干本,用去699元;语文组购买了A、B两种文学书籍若干本,用去6138元,已知A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同,若甲种书的单价比乙种书的单价多7元,则乙种书籍比甲种书籍多买了_____本.
【详解】
解:设乙种书籍的单价为每本????元,则甲种书籍的单价为(????+????)元,A种书籍的单价为每本????元,B种书籍的单价为(????+????)元,设A购买了????本,B购买了????本,则甲购买了????本,乙购买了????本,所以:
?
②-①得:????????+????(????+????)?????(????+????)?????????=????????????????
所以:????(?????????)=????????????????,所以:?????????=????????????.所以:乙比甲多买了????????????本.
?
课堂小结
再见
