9.1.1 不等式及其解集 课件(共20张PPT)
文档属性
| 名称 | 9.1.1 不等式及其解集 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 09:28:41 | ||
图片预览







文档简介
9.1.1 不等式及其解集
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
1、理解不等式的含义。
2、理解不等式的解与不等式的解集的含义,利用数轴表示不等式的解集。
3、能根据表示不等的语句列出不等关系式。
理解不等式的解与不等式的解集的含义。(重点)
利用数轴表示不等式的解集。(难点)
学习目标
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50km所用的时间不到40分钟(????????小时),即
?
?????????????
新课导入
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶40分钟(????????小时)的路程要超过50km,即
?
????????x>50 ②
?
探究新知
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
?????????????
????????x>50 ②
?
结合实际问题,观察式子①和②,你发现了什么?
式子①和②从不同的角度表示了车速应满足的条件。
不等式
用>或<号表示大小关系或用≠号表示不等关系的式子叫不等式。
【注意事项】
1. “≤”、“≥”也可以表示大小关系。
2. 不等式中可以含有未知数,也可以不含未知数。
1、下列式子中哪些是不等式?
(1)7>4 (2)x?+3>0 (3)3x?+2x (4)x<8x+6 (5)2x=3x+5 (6)x?+x(9)3x-8<4x+1 (10)3a-17≤1
2、用不等式表示:
⑴ x与7的和是正数;
⑵ y的3倍与3的和小于5;
⑶ y的5倍与x的3倍的和是非负数;
x+7>0
3y+3<5
5y+3x≥0
针对练习
小强准备和父母坐火车去北京旅游。若小强身高为 x 米,那么:
免票
半票
全票
儿童火车票身高新标准
1)当x满足 时,他可免票。
2)当x满足 时,他该买半票。
根据儿童火车票身高新标准
3)当x满足 时,他该买全票。
x<1.2 m
x≥1.5 m
1.2≤x<1.5 m
探究新知
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
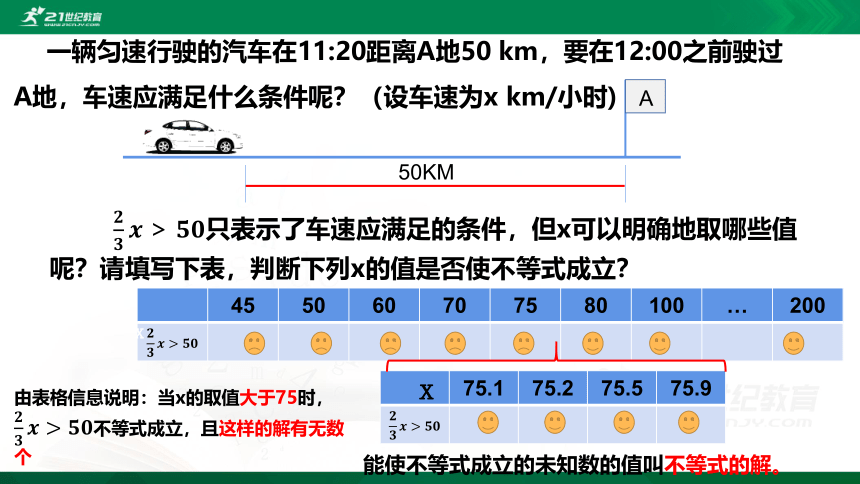
????????????????????>????????只表示了车速应满足的条件,但x可以明确地取哪些值呢?请填写下表,判断下列x的值是否使不等式成立?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
45
50
60
70
75
80
100
…
200
????????????>????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
45
50
60
70
75
80
100
…
200
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
75.1
75.2
75.5
75.9
????????????>????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
75.1
75.2
75.5
75.9
x
x
由表格信息说明:当x的取值大于75时, ????????????>????????不等式成立,且这样的解有无数个
?
能使不等式成立的未知数的值叫不等式的解。
A
50KM
不等式的解集及解不等式
不等式的解集:一个含有未知数的不等式的所有解组成这个不等式的解集。(如x>75)
解不等式:求不等式的解集的过程。
表示不等式的解集
1.代数表示(x>a, x75
2.几何表示(数轴表示法)
例:
0
75
总结: 用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
【注意事项】(易错点)
1.在表示75的点上画空心圆圈,表示不包含这一点。
2.在表示75的点上画实心圆圈,表示包含这一点。
3.大于向右画(开口向右),小于向左画(开口向左)。
(利用数轴表示不等式)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式的解集
数轴表示
x>a
xx≥a
x≤a
○
a
○
a
a
a
1.用不等式表示如图的解集,其中正确的是( )
A.????>???? B.x≥2
C.?????
【解析】
解:根据“开口向左、实心”的特征可得解集为x≤2,故选D.
课堂练习
2.下列不等式的解集中,不包括-4的是( )
A.????≤????? B.????≥?????
C.????≤????? D.????>?????
?
【答案】C
【详解】
解:根据题意,不包括-4即-4不在解集内,
只有C选项,x≤ - 5,不包括-4.
故选:C.
3、尝试在数轴上画出下列不等式的解集
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式的解集
数轴表示
x>4
x<4
x≥4
x≤4
○
4
○
4
4
4
4、下面列出的不等式中,正确的是( )
A.“m不是正数”表示为m<0 B.“m不大于3”表示为m<3
C.“n与4的差是负数”表示为n﹣4<0
D.“n不等于6”表示为n>6
【详解】
A. “m不是正数”表示为????≤????, 故错误.
B. “m不大于3”表示为????≤????,故错误.
C. “n与4的差是负数”表示为n﹣4<0,正确.
D. “n不等于6”表示为????≠????,故错误.故选:C.
?
5.下列说法正确的是( )
A.x=﹣3是不等式x>﹣2的一个解 B.x=﹣1是不等式x>﹣2的一个解
C.不等式x>﹣2的解是x=﹣3 D.不等式x>﹣2的解是x=﹣1
【详解】
解:A.x=﹣3不是不等式x>﹣2的一个解,此选项错误;
B.x=﹣1是不等式x>﹣2的一个解,此选项正确;
C.不等式x>﹣2的解有无数个,此选项错误;
D.不等式x>﹣2的解有无数个,此选项错误;故选:B.
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集。
三、不等式的解集及解不等式的概念
求不等式的解集的过程叫解不等式。
四、解集的表示方法:
第一种:用式子(如x>2),即用最简形式的不等式(如x>a或x第二种:用数轴,一般标出数轴上某一区间,其中的点对应的数值都是不等式的解。
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解。
二、不等式的解的概念
像156>155,155<156,x>50,这样,我们把用符号“>”或“<”连接而成的式子叫做不等式。像a≠2这样的式子也叫做不等式。
一、不等式的概念
课堂小结
再见
第九章 不等式与不等式组
2021年春人教版七年级(下)数学
1、理解不等式的含义。
2、理解不等式的解与不等式的解集的含义,利用数轴表示不等式的解集。
3、能根据表示不等的语句列出不等关系式。
理解不等式的解与不等式的解集的含义。(重点)
利用数轴表示不等式的解集。(难点)
学习目标
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50km所用的时间不到40分钟(????????小时),即
?
?????????????
新课导入
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶40分钟(????????小时)的路程要超过50km,即
?
????????x>50 ②
?
探究新知
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
A
50KM
?????????????
????????x>50 ②
?
结合实际问题,观察式子①和②,你发现了什么?
式子①和②从不同的角度表示了车速应满足的条件。
不等式
用>或<号表示大小关系或用≠号表示不等关系的式子叫不等式。
【注意事项】
1. “≤”、“≥”也可以表示大小关系。
2. 不等式中可以含有未知数,也可以不含未知数。
1、下列式子中哪些是不等式?
(1)7>4 (2)x?+3>0 (3)3x?+2x (4)x<8x+6 (5)2x=3x+5 (6)x?+x
2、用不等式表示:
⑴ x与7的和是正数;
⑵ y的3倍与3的和小于5;
⑶ y的5倍与x的3倍的和是非负数;
x+7>0
3y+3<5
5y+3x≥0
针对练习
小强准备和父母坐火车去北京旅游。若小强身高为 x 米,那么:
免票
半票
全票
儿童火车票身高新标准
1)当x满足 时,他可免票。
2)当x满足 时,他该买半票。
根据儿童火车票身高新标准
3)当x满足 时,他该买全票。
x<1.2 m
x≥1.5 m
1.2≤x<1.5 m
探究新知
一辆匀速行驶的汽车在11:20距离A地50 km,要在12:00之前驶过A地,车速应满足什么条件呢?(设车速为x km/小时)
????????????????????>????????只表示了车速应满足的条件,但x可以明确地取哪些值呢?请填写下表,判断下列x的值是否使不等式成立?
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
45
50
60
70
75
80
100
…
200
????????????>????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
45
50
60
70
75
80
100
…
200
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
75.1
75.2
75.5
75.9
????????????>????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
75.1
75.2
75.5
75.9
x
x
由表格信息说明:当x的取值大于75时, ????????????>????????不等式成立,且这样的解有无数个
?
能使不等式成立的未知数的值叫不等式的解。
A
50KM
不等式的解集及解不等式
不等式的解集:一个含有未知数的不等式的所有解组成这个不等式的解集。(如x>75)
解不等式:求不等式的解集的过程。
表示不等式的解集
1.代数表示(x>a, x
2.几何表示(数轴表示法)
例:
0
75
总结: 用数轴表示不等式的解集的步骤:
第一步:画数轴;
第二步:定界点;
第三步:定方向.
【注意事项】(易错点)
1.在表示75的点上画空心圆圈,表示不包含这一点。
2.在表示75的点上画实心圆圈,表示包含这一点。
3.大于向右画(开口向右),小于向左画(开口向左)。
(利用数轴表示不等式)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式的解集
数轴表示
x>a
xx≥a
x≤a
○
a
○
a
a
a
1.用不等式表示如图的解集,其中正确的是( )
A.????>???? B.x≥2
C.?????
【解析】
解:根据“开口向左、实心”的特征可得解集为x≤2,故选D.
课堂练习
2.下列不等式的解集中,不包括-4的是( )
A.????≤????? B.????≥?????
C.????≤????? D.????>?????
?
【答案】C
【详解】
解:根据题意,不包括-4即-4不在解集内,
只有C选项,x≤ - 5,不包括-4.
故选:C.
3、尝试在数轴上画出下列不等式的解集
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式的解集
数轴表示
x>4
x<4
x≥4
x≤4
○
4
○
4
4
4
4、下面列出的不等式中,正确的是( )
A.“m不是正数”表示为m<0 B.“m不大于3”表示为m<3
C.“n与4的差是负数”表示为n﹣4<0
D.“n不等于6”表示为n>6
【详解】
A. “m不是正数”表示为????≤????, 故错误.
B. “m不大于3”表示为????≤????,故错误.
C. “n与4的差是负数”表示为n﹣4<0,正确.
D. “n不等于6”表示为????≠????,故错误.故选:C.
?
5.下列说法正确的是( )
A.x=﹣3是不等式x>﹣2的一个解 B.x=﹣1是不等式x>﹣2的一个解
C.不等式x>﹣2的解是x=﹣3 D.不等式x>﹣2的解是x=﹣1
【详解】
解:A.x=﹣3不是不等式x>﹣2的一个解,此选项错误;
B.x=﹣1是不等式x>﹣2的一个解,此选项正确;
C.不等式x>﹣2的解有无数个,此选项错误;
D.不等式x>﹣2的解有无数个,此选项错误;故选:B.
一般的,一个含有未知数的不等式的所有的解,组成这个不等式的解集。
三、不等式的解集及解不等式的概念
求不等式的解集的过程叫解不等式。
四、解集的表示方法:
第一种:用式子(如x>2),即用最简形式的不等式(如x>a或x
我们曾经学过“使方程两边相等的未知数的值就是方程的解”,与方程类似 , 能使不等式成立的未知数的值叫不等式的解。
二、不等式的解的概念
像156>155,155<156,x>50,这样,我们把用符号“>”或“<”连接而成的式子叫做不等式。像a≠2这样的式子也叫做不等式。
一、不等式的概念
课堂小结
再见
