人教版 九年级上册 第二十二章 二次函数 22.1 二次函数的图象和性质22.1.1二次函数(共20张)
文档属性
| 名称 | 人教版 九年级上册 第二十二章 二次函数 22.1 二次函数的图象和性质22.1.1二次函数(共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 12:45:17 | ||
图片预览







文档简介
(共20张PPT)
22.1.1
二次函数
22.1
二次函数的图象和性质
第22章
二次函数
1、函数的定义是什么?我们学习过哪些函数?它们的解析式如何表示?
一、知识回顾
函数的定义:在变化过程中,有两个变量x和y,当x每确定一个值时,y都有唯一一个值与其对应,我们称x为自变量,y为x的函数
2、一次函数有哪些主要特征?
一次函数:y=kx+b(k≠0)
b=0
正比例函数:y=kx
(k≠0)
①含未知数的代数式为整式;
②自变量
x的系数k≠0
③自变量
x的次数是1
(1)
y
=
2x+1
(3)
y
=
-4x
(4)
y
=
ax+1
(2)
其中,y是x的一次函数有_________
下列关系式:
y=kx+b(k≠0)
(1)、
(3)
一次函数的一般形式是_____________
变量之间的关系
函数
一次函数
概念
图象和性质
与相应方程的联系
实际问题
学习历程
篮球和水珠在空中走过一条曲线.在这条曲线的各个位置上,篮球(水珠)的竖直高度y与它距离投出位置(喷头)的水平距离x之间有什么关系?
上面问题中变量之间的关系可以用二次函数来表示.这就是我们今天要学习的内容.
一次投篮过程
广场喷水池喷出的水珠
导入课题
新课导入
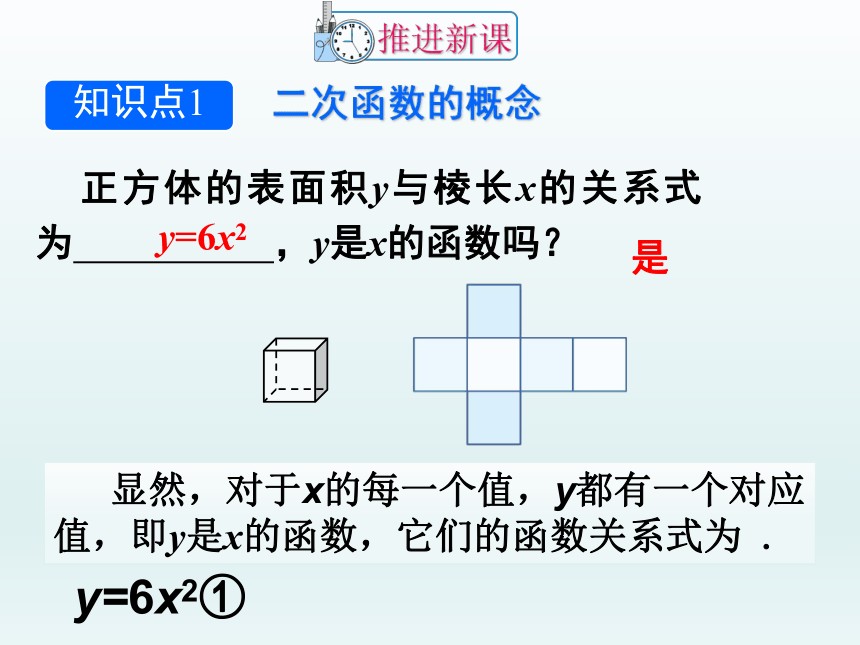
正方体的表面积y与棱长x的关系式为
,y是x的函数吗?
推进新课
知识点1
二次函数的概念
y=6x2
是
显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的函数关系式为
.
y=6x2①
我们再来看几个问题。
问题1
n个球队参加比赛,每两队之间进行一场比赛。比赛的场次数m与球队数n有什么关系?
m是n的函数吗?
即,
显然,对于n的每一个值,m都有一个对应值,即m是n的函数
②
问题2
某种产品现在的年产量是
20
t,计划今后两年增加产量.如果每年都比上一年的产量增加
x
倍,那么两年后这种产品的产量
y
将随计划所定的x
的值而确定,y
与
x
之间的关系应怎样表示?
分析:这种产品的原产量是20t,一
年后的产量是_________t,再经过
一年后的产量是__________
t,即两年后的产量
为__________________.
20(1+x)
20(1+x)(1+x)
y
=
20(1+x)2
③
即:
③式表示了两年后的产量
y
与计划增产的
倍数
x
之间的关系,对于
x
的每一个值,y
都
有唯一的值与之对应,即
y
是
x
的函数.
上述三个函数都是用自变量的二次式表示的。一般地,形如y=ax?+bx+c(a,b,c为常数,a≠0)
的函数,叫做二次函数。其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项。
二次项
一次项
常数项
函数y=6x2
,
,
y=20x2+40x+20
,
有什么共同点?
思考
(1)a,b,c
为常数,且a
≠
0,但b、c可以取0
(2)各项均为整式.
(3)自变量的最高次数是2,取值范围是全体实数.
注意:
考查角度一
二次函数的识别
下列函数中是二次函数的有
。
√
a=0
×
最高次数是4
×
×
√
①⑤
×
总结:判断一个函数是否是二次函数步骤
(1)、整理并判断右边含自变量的代数式是否是整式;
(3)、判断二次项系数是否不等于0.
(2)、判断自变量的最高次数是否是2;
函数解析式
二次项系数a
一次项系数b
常数项
c
0
0
2
4
2
-1
58
-112
13
0
练习1、填表:
二次函数
y=a
x
?
+
b
x
+
c
中:
a≠0,但
b、c可以为0.
解:依题意,得
解得a=-1.
思考:当a为何值时,该函数是正比例函数?
考查角度二
应用二次函数的概念求相关字母的
取值(或范围)
解:依题意,得
解得a=0
练习:
若
(1)m取什么值时,此函数是二次函数?
(2)m取什么值时,此函数是一次函数?
解:(1)依题意,得
解得m=-3.
(2)依题意,得
考查角度三
求二次函数的函数值
一辆汽车的行驶距离s(单位::m)关于行驶时间t(单位:s)的函数解析式是
,经过12s汽车行驶了多远?行驶380m需要多少时间?
例2
用总长为
60
m
的篱笆围成矩形场
地,场地面积
S(m?)与矩形一边长a(m)
之间的关系是什么?是哪种函数关系?
并求出自变量的取值范围?
解:S
=
a(
-a)
=
a(30
-a)
=
-a?
+
30
a
自变量的取值范围:0<a<30
是二次函数关系式。
自变量的取值范围应符合实际意义
根据具体问题确定二次函数解析式
知识点2
根据实际问题建立二次函数模型的一般步骤:
①仔细审题,分析数量之间的关系,将文字语言转化为符号语言;
②根据实际问题中的等量关系,列二次函数关系式,并化成一般形式;
③联系实际,确定自变量的取值范围。
1.一个圆柱的高等于底面半径,写出它的表面积
S
与半径
r之间的关系式.
随堂练习
r
r
2.矩形绿地的长、宽各增加
x
m,写出扩充后的绿地的面积
y
与
x的关系式.
20
m
x
m
30
m
x
m
(r>0)
(x≥0)
提高练习
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,写出△PBQ的面积S与出发时间t(s)的函数关系式及t的取值范围.
解:依题意,得AP=2t,
BQ=4t.
∵AB=12,
∴PB=12-2t,
t的取值范围为0≤t≤6.
∴
∴
课堂小结
1.二次函数的概念是什么?
2.辨析二次函数时应注意哪些问题?
作业
1.(必做)课本41页第1、2题
2.(选做)课本42页第12题
22.1.1
二次函数
22.1
二次函数的图象和性质
第22章
二次函数
1、函数的定义是什么?我们学习过哪些函数?它们的解析式如何表示?
一、知识回顾
函数的定义:在变化过程中,有两个变量x和y,当x每确定一个值时,y都有唯一一个值与其对应,我们称x为自变量,y为x的函数
2、一次函数有哪些主要特征?
一次函数:y=kx+b(k≠0)
b=0
正比例函数:y=kx
(k≠0)
①含未知数的代数式为整式;
②自变量
x的系数k≠0
③自变量
x的次数是1
(1)
y
=
2x+1
(3)
y
=
-4x
(4)
y
=
ax+1
(2)
其中,y是x的一次函数有_________
下列关系式:
y=kx+b(k≠0)
(1)、
(3)
一次函数的一般形式是_____________
变量之间的关系
函数
一次函数
概念
图象和性质
与相应方程的联系
实际问题
学习历程
篮球和水珠在空中走过一条曲线.在这条曲线的各个位置上,篮球(水珠)的竖直高度y与它距离投出位置(喷头)的水平距离x之间有什么关系?
上面问题中变量之间的关系可以用二次函数来表示.这就是我们今天要学习的内容.
一次投篮过程
广场喷水池喷出的水珠
导入课题
新课导入
正方体的表面积y与棱长x的关系式为
,y是x的函数吗?
推进新课
知识点1
二次函数的概念
y=6x2
是
显然,对于x的每一个值,y都有一个对应值,即y是x的函数,它们的函数关系式为
.
y=6x2①
我们再来看几个问题。
问题1
n个球队参加比赛,每两队之间进行一场比赛。比赛的场次数m与球队数n有什么关系?
m是n的函数吗?
即,
显然,对于n的每一个值,m都有一个对应值,即m是n的函数
②
问题2
某种产品现在的年产量是
20
t,计划今后两年增加产量.如果每年都比上一年的产量增加
x
倍,那么两年后这种产品的产量
y
将随计划所定的x
的值而确定,y
与
x
之间的关系应怎样表示?
分析:这种产品的原产量是20t,一
年后的产量是_________t,再经过
一年后的产量是__________
t,即两年后的产量
为__________________.
20(1+x)
20(1+x)(1+x)
y
=
20(1+x)2
③
即:
③式表示了两年后的产量
y
与计划增产的
倍数
x
之间的关系,对于
x
的每一个值,y
都
有唯一的值与之对应,即
y
是
x
的函数.
上述三个函数都是用自变量的二次式表示的。一般地,形如y=ax?+bx+c(a,b,c为常数,a≠0)
的函数,叫做二次函数。其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项。
二次项
一次项
常数项
函数y=6x2
,
,
y=20x2+40x+20
,
有什么共同点?
思考
(1)a,b,c
为常数,且a
≠
0,但b、c可以取0
(2)各项均为整式.
(3)自变量的最高次数是2,取值范围是全体实数.
注意:
考查角度一
二次函数的识别
下列函数中是二次函数的有
。
√
a=0
×
最高次数是4
×
×
√
①⑤
×
总结:判断一个函数是否是二次函数步骤
(1)、整理并判断右边含自变量的代数式是否是整式;
(3)、判断二次项系数是否不等于0.
(2)、判断自变量的最高次数是否是2;
函数解析式
二次项系数a
一次项系数b
常数项
c
0
0
2
4
2
-1
58
-112
13
0
练习1、填表:
二次函数
y=a
x
?
+
b
x
+
c
中:
a≠0,但
b、c可以为0.
解:依题意,得
解得a=-1.
思考:当a为何值时,该函数是正比例函数?
考查角度二
应用二次函数的概念求相关字母的
取值(或范围)
解:依题意,得
解得a=0
练习:
若
(1)m取什么值时,此函数是二次函数?
(2)m取什么值时,此函数是一次函数?
解:(1)依题意,得
解得m=-3.
(2)依题意,得
考查角度三
求二次函数的函数值
一辆汽车的行驶距离s(单位::m)关于行驶时间t(单位:s)的函数解析式是
,经过12s汽车行驶了多远?行驶380m需要多少时间?
例2
用总长为
60
m
的篱笆围成矩形场
地,场地面积
S(m?)与矩形一边长a(m)
之间的关系是什么?是哪种函数关系?
并求出自变量的取值范围?
解:S
=
a(
-a)
=
a(30
-a)
=
-a?
+
30
a
自变量的取值范围:0<a<30
是二次函数关系式。
自变量的取值范围应符合实际意义
根据具体问题确定二次函数解析式
知识点2
根据实际问题建立二次函数模型的一般步骤:
①仔细审题,分析数量之间的关系,将文字语言转化为符号语言;
②根据实际问题中的等量关系,列二次函数关系式,并化成一般形式;
③联系实际,确定自变量的取值范围。
1.一个圆柱的高等于底面半径,写出它的表面积
S
与半径
r之间的关系式.
随堂练习
r
r
2.矩形绿地的长、宽各增加
x
m,写出扩充后的绿地的面积
y
与
x的关系式.
20
m
x
m
30
m
x
m
(r>0)
(x≥0)
提高练习
如图,在△ABC中,∠B=90°,AB=12,BC=24,动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动,动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动,如果点P、Q分别从点A、B同时出发,写出△PBQ的面积S与出发时间t(s)的函数关系式及t的取值范围.
解:依题意,得AP=2t,
BQ=4t.
∵AB=12,
∴PB=12-2t,
t的取值范围为0≤t≤6.
∴
∴
课堂小结
1.二次函数的概念是什么?
2.辨析二次函数时应注意哪些问题?
作业
1.(必做)课本41页第1、2题
2.(选做)课本42页第12题
同课章节目录
