6.2.2排列(2)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(共14张PPT)
文档属性
| 名称 | 6.2.2排列(2)-【新教材】2020-2021学年人教A版(2019)高中数学选择性必修第三册课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 426.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-26 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
6.2.2
排
列
高二数学选择性必修
第三册
第六章
计数原理
学习目标
1.掌握排列的概念和排列数的公式;
2.能正确利用排列数公式进行计算和证明,
能解决简单的排列问题.
3.核心素养:
数学抽象、数学运算。
从n个不同元素中,任取m(
)个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1.排列的定义:
2.排列数的定义:
从n个不同元素中,任取m(
)个元素的所有排列的个数叫做从n个元素中取出m个元素的排列数
3.有关公式:
(2).排列数公式:
一、回顾旧知
1.例1.某年全国足球甲级A组联赛共有14个队参加,
每队要与其余各队在主、客场分别比赛一次,
共进行多少场比赛?
解:14个队中任意两队进行1次主场比赛与1次客场
比赛,对应于从14个元素中任取2个元素的一
个排列,因此,比赛的总场次是
二、巩固应用
2.例2.(1)从5本不同的书中选3本送给3名同学,每人各1本,
共有多少种不同的送法?
(2)从5种不同的书中买3本送给3名同学,每人各1本,
共有多少种不同的送法?
=
5×4×3=
60
被选元素可重复选取,不是排列问题
5×5×5=
125
“从5个不同元素中选出3并按顺序排列”
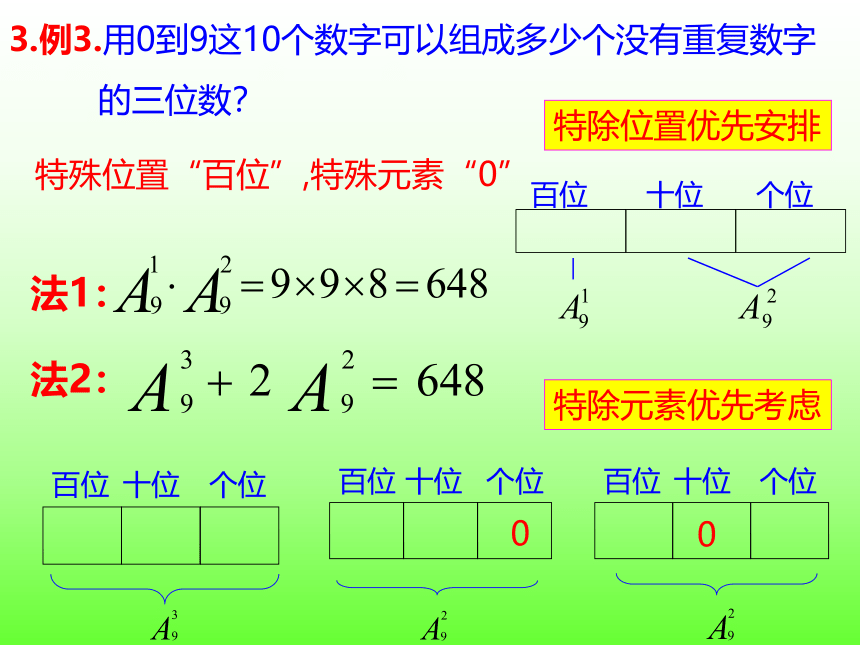
3.例3.用0到9这10个数字可以组成多少个没有重复数字
的三位数?
特殊位置“百位”,特殊元素“0”
百位
十位
个位
法1:
法2:
百位
十位
个位
0
百位
十位
个位
特除位置优先安排
特除元素优先考虑
0
百位
十位
个位
3.例3.用0到9这10个数字可以组成多少个没有重复数字
的三位数?
特殊位置“百位”,特殊元素“0”
法3:
正难则反(间接法)
对于有限制条件的排列问题,必须遵循“特殊元素优先考虑,特殊位置优先安排”,并注意“合理分类,准确分步”,做到“不重不漏,步骤完整”,适当考虑“正难则反”
.
百位
十位
个位
千位
万位
4.变式练习:由数字1、2、3、4、5组成没有重复数字
的五位数,其中小于50000的偶数共有多少个?
有约束条件的排列问题
4.变式练习:由数字1、2、3、4、5组成没有重复数字
的五位数,其中小于50000的偶数共有多少个?
有约束条件的排列问题
百位
十位
个位
千位
万位
5.例4.有4个男生和3个女生排成一排,按下列要求各有
多少种不同排法:
(1)男甲排在正中间;
(2)男甲不在排头,女乙不在排尾;
(3)三个女生排在一起;
(4)三个女生两两都不相邻;
对于相邻问题,常用“捆绑法”
有约束条件的排列问题
对于不相邻问题,常用“插空法”
6.变式练习:有5名男生,4名女生排队.
(1)从中选出3人排成一排,有多少
种排法?
(2)全部排成一排,有多少种排法?
(3)排成两排,前排4人,后排5人,有多少种排法?
7.变式练习.6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙丁两本书必须相邻,则不同的摆放方法有
种.
解:完成这件事可分三步:
第一步:将甲、乙两本书摆放在两端,有
=2种摆法.
第二步:将丙、丁两本书看成一个整体,考虑两本书
顺序,有
=2种摆法.
第三步:将丙、丁这个整体与另外两本书全排列,摆放在中间3个位置,有
=6种摆法.
根据分步乘法计数原理,
共有
=
2×2×6=24种不同的摆放方法.
24
1.对有约束条件的排列问题,应注意如下类型:
⑴.某些元素不能在或必须排列在某一位置;
⑵.某些元素要求连排(即必须相邻);
⑶.某些元素要求分离(即不能相邻);
2.基本的解题方法:
(1).有特殊元素或特殊位置的排列问题,通常
是先排特殊元素或特殊位置,称为优先处
理特殊元素(位置)法(优先法);
特殊元素,特殊位置优先安排策略
三、课堂小结
2.基本的解题方法:
(2).某些元素要求必须相邻时,可以先将这些元素
看作一个元素,与其他元素排列后,再考虑相
邻元素的内部排列,这种方法称为“捆绑法”;
相邻问题捆绑处理的策略
(3).某些元素不相邻排列时,可以先排其他元素,再将
这些不相邻元素插入空挡,这种方法称为“插空法”;
不相邻问题插空处理的策略
三、课堂小结
作业:课本P20
练习
2、3题
6.2.2
排
列
高二数学选择性必修
第三册
第六章
计数原理
学习目标
1.掌握排列的概念和排列数的公式;
2.能正确利用排列数公式进行计算和证明,
能解决简单的排列问题.
3.核心素养:
数学抽象、数学运算。
从n个不同元素中,任取m(
)个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1.排列的定义:
2.排列数的定义:
从n个不同元素中,任取m(
)个元素的所有排列的个数叫做从n个元素中取出m个元素的排列数
3.有关公式:
(2).排列数公式:
一、回顾旧知
1.例1.某年全国足球甲级A组联赛共有14个队参加,
每队要与其余各队在主、客场分别比赛一次,
共进行多少场比赛?
解:14个队中任意两队进行1次主场比赛与1次客场
比赛,对应于从14个元素中任取2个元素的一
个排列,因此,比赛的总场次是
二、巩固应用
2.例2.(1)从5本不同的书中选3本送给3名同学,每人各1本,
共有多少种不同的送法?
(2)从5种不同的书中买3本送给3名同学,每人各1本,
共有多少种不同的送法?
=
5×4×3=
60
被选元素可重复选取,不是排列问题
5×5×5=
125
“从5个不同元素中选出3并按顺序排列”
3.例3.用0到9这10个数字可以组成多少个没有重复数字
的三位数?
特殊位置“百位”,特殊元素“0”
百位
十位
个位
法1:
法2:
百位
十位
个位
0
百位
十位
个位
特除位置优先安排
特除元素优先考虑
0
百位
十位
个位
3.例3.用0到9这10个数字可以组成多少个没有重复数字
的三位数?
特殊位置“百位”,特殊元素“0”
法3:
正难则反(间接法)
对于有限制条件的排列问题,必须遵循“特殊元素优先考虑,特殊位置优先安排”,并注意“合理分类,准确分步”,做到“不重不漏,步骤完整”,适当考虑“正难则反”
.
百位
十位
个位
千位
万位
4.变式练习:由数字1、2、3、4、5组成没有重复数字
的五位数,其中小于50000的偶数共有多少个?
有约束条件的排列问题
4.变式练习:由数字1、2、3、4、5组成没有重复数字
的五位数,其中小于50000的偶数共有多少个?
有约束条件的排列问题
百位
十位
个位
千位
万位
5.例4.有4个男生和3个女生排成一排,按下列要求各有
多少种不同排法:
(1)男甲排在正中间;
(2)男甲不在排头,女乙不在排尾;
(3)三个女生排在一起;
(4)三个女生两两都不相邻;
对于相邻问题,常用“捆绑法”
有约束条件的排列问题
对于不相邻问题,常用“插空法”
6.变式练习:有5名男生,4名女生排队.
(1)从中选出3人排成一排,有多少
种排法?
(2)全部排成一排,有多少种排法?
(3)排成两排,前排4人,后排5人,有多少种排法?
7.变式练习.6本不同的书在书桌上摆成一排,要求甲、乙两本书必须放在两端,丙丁两本书必须相邻,则不同的摆放方法有
种.
解:完成这件事可分三步:
第一步:将甲、乙两本书摆放在两端,有
=2种摆法.
第二步:将丙、丁两本书看成一个整体,考虑两本书
顺序,有
=2种摆法.
第三步:将丙、丁这个整体与另外两本书全排列,摆放在中间3个位置,有
=6种摆法.
根据分步乘法计数原理,
共有
=
2×2×6=24种不同的摆放方法.
24
1.对有约束条件的排列问题,应注意如下类型:
⑴.某些元素不能在或必须排列在某一位置;
⑵.某些元素要求连排(即必须相邻);
⑶.某些元素要求分离(即不能相邻);
2.基本的解题方法:
(1).有特殊元素或特殊位置的排列问题,通常
是先排特殊元素或特殊位置,称为优先处
理特殊元素(位置)法(优先法);
特殊元素,特殊位置优先安排策略
三、课堂小结
2.基本的解题方法:
(2).某些元素要求必须相邻时,可以先将这些元素
看作一个元素,与其他元素排列后,再考虑相
邻元素的内部排列,这种方法称为“捆绑法”;
相邻问题捆绑处理的策略
(3).某些元素不相邻排列时,可以先排其他元素,再将
这些不相邻元素插入空挡,这种方法称为“插空法”;
不相邻问题插空处理的策略
三、课堂小结
作业:课本P20
练习
2、3题
