7.1.1数系的扩充和复数的概念 课件(共26张PPT)2020-2021学年高一数学人教A版(2019)必修第二册
文档属性
| 名称 | 7.1.1数系的扩充和复数的概念 课件(共26张PPT)2020-2021学年高一数学人教A版(2019)必修第二册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 21:07:43 | ||
图片预览








文档简介
(共26张PPT)
7.1
复数的概念
7.1.1
数系的扩充和复数的概念
课标对本节的要求:
1.了解复数的概念:
能类比有有理数系扩充到实数系的过程和方法,通过方程的解,认识复数;
2.理解复数:
能描述复数代数式表示结构特征,能判断复数的实部、虚部;知道复数集,实数集,虚数集,纯虚数集的关系;
3.理解复数相等:
能说明复数相等的含义,会判断复数相等。
我们知道,对于实系数一元二次方程ax2+bx+c=0,当?=b2-4ac直到1545年,数学家在研究实系数一元三次方程的求根公式时,同时用求根公式法,因式分解法解同一个特殊的一元三次方程时,得到了一些无法理解的结果,于是这个问题就再也无法回避了。
例如,方程x3-15x+4=0
用求根公式法可得以下三个根:
而用因式分解法又可得(x-4)(x2+4x+1)=0,此时三个根为:
本章及本节的引入
要解决这个问题的过程中,就必须排除许多困扰,如负实数能不能开平方?如何开方?负实数开平方的意义是什么?等等
。
本章我们就开学习相关的一些简单知识,感受引引入复数的必要性,了解复数系的扩充过程和方法,研究复数的表示、运算及其几何意义,体会数形的融合。
你能回想起数系的扩展过程吗?
在从自然数集扩充到实数集的过程中,每次引入新数后,原有的加法和乘法的运算律都没有变。
从社会实践来看,数的扩充都是为了解决生产生活中的问题,数集的每一次扩充,都是在原数集的基础上添加新数得到的。
因此,在解决判别式小于0实系数一元二次方程时,一个自然的想法就是引入一个新数,把原有的实数集进行扩充,从而使方程变得可解。复数的引入就与这种想法直接相关。
问题1:从方程的角度看,负实数能不能开平方的问题可以归结为方程“x2+a=0”(其中a>0)有没有解的问题,从而进一步归结为方程“x2+1=0”有没有解的问题。这是为什么?
当a>0时,-a<0
”实数-a能不能开平方”的问题,就是“-a有没有平方根”的问题。
而根据平方根的定义,就是“是否存在一个数x使x2=-a”,即”方程x2+a=0(其中a>0)有没有解”的问题。
因此
”方程x2+a=0(其中a>0)有没有解”的问题,可最终归结为“x2+1=0”有没有解的问题。
探究新知
问题2:从我们知道,方程x2+1=0在实数集是无解的,联系到自然数集到实数集的扩充过程,是否能引入新数,将实数集适当地进一步扩充,使这个方程在这个新的数集中有解的?
1637年,法国数学家笛卡尔,在《几何学》给出“虚数”这一名称,使“虚的数”与“实的数”相对应,从此,虚数才流传开来。
1748年,瑞典数学家欧拉在发现了著名的关系式(欧拉公式)。
1777年,欧拉在《微分公式》一文中第一次用”i“来表示”-1的平方根“,首创了用符号”i“作为虚数的单位。
添加新数i后,你最希望这个有什么运算性质?
i
可以与实数之间进行加法和乘法运算,并希望实数原有的关于加法和乘的运算律仍然成立.
虚数
虚数单位i
数
i
叫做虚数单位,并规定:
(1)它的平方等于
-1,即
(2)i
可以与实数进行加法和乘法运算,且实数原有的有关加法和乘法的运算律仍然成立.
问题3:实数系经过扩充以后,按照以上的(2),这个新数系会由哪些数来组成呢?
你能写出类似于以上数的形式吗?说说理由。
出现新数喽!
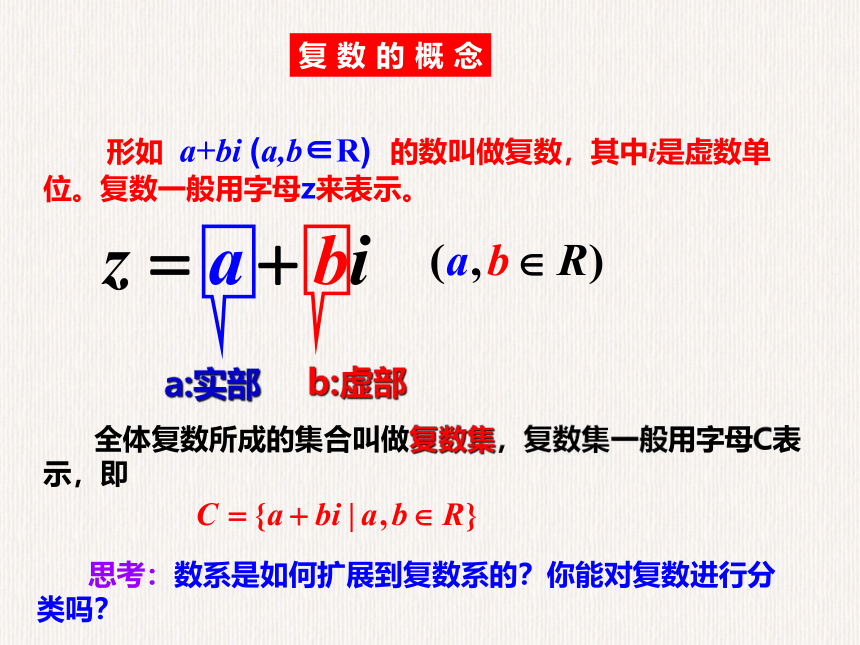
复数的概念
形如
a+bi
(a,b∈R)
的数叫做复数,其中i是虚数单位。复数一般用字母z来表示。
全体复数所成的集合叫做复数集,复数集一般用字母C表示,即
a:实部
b:虚部
思考:数系是如何扩展到复数系的?你能对复数进行分类吗?
复数的分类
实数
虚数
纯虚数
非纯虚数
(a∈R,b∈R)
纯虚数集
引入虚数后,实数原有的加法和乘法的运算律仍然成立。
例1.写出下列复数的实部和虚部,并指出哪些是实数,哪些是虚数,哪些是纯虚数?
例析
解:
两个复数相等的充要条件是它们的实部和虚部分别相等。即
说明:
(1)两个复数一般不能比较大小(除非两个均为实数)
(2)复数相等定义的作用:
1)判断两个复数是否相等;
2)求某些复数值。利用实部和虚部分别相等转化成方程(组),通过解方程(组),求出复数。
复数相等
例2.实数m取什么值时,复数
z=m+1+(m-1)i
是下列数?
(1)实数?
(2)虚数?
(3)纯虚数?
(1)由m-1=0得,m=1
∴当
m=1时,z为实数。
(2)由m-1≠0得,m≠1
∴当
m≠1时,z为虚数。
(3)由题意得
解得m=-1
∴当
m=-1时,z为纯虚数
例析
解:
例3.已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,其中x,y∈R,求x,y.
由复数相等的定义得
解得
解:
1.求满足下列条件的实数x,y的值:
(1)(x+y)+(y-1)i=(2x+3y)+(2y+1)i
(2)(x+y-3)+(x-2)i=0
练习
解:(1)由复数相等的定义得
解得
(2)由复数相等的定义得
解得
2.当m为何实数时,复数z=(m2+m-2)+(m2-1)i
是
(1)实数?
(2)虚数
?
(3)纯虚数?
4.复数相等的含义.
复数,复数的实部
、虚部
3.复数的分类;
1.虚数单位i的引入和数系扩充;
2.复数的基本概念;
小结
阅读资料
作业
教材P73习题第1,2,3题
16世纪意大利米兰学者(Jerome
Cardan1501—1576)在1545年发表的《重要的艺术》一书中,公布了三次方程的一般解法,被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家,并且在讨论是否可能把10分成两部分,使它们的乘积等于40时,他把答案写成
,尽管他认为和这两个表示式是没有意义的、想象的、虚无飘渺的,但他还是把10分成了两部分,并使它们的乘积等于40。
给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650),他在《几何学》(1637年发表)中使“虚的数”与“实的数”相对应,从此,虚数才流传开来。
数系中发现一颗新星——虚数,于是引起了数学界的一片困惑,很多大数学家都不承认虚数。
德国数学家(1646—1716)在1702年说:“虚数是神灵遁迹的精微而奇异的隐避所,它大概是存在和虚妄两界中的两栖物”。
复数的起源
资料1
返回
瑞士数学大师(1707—1783)说;“一切形如i的式子都是不可能有的,它是想象的数,因为它们所表示的是负数的平方根。对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么,它们纯属虚幻。”
然而,真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地。
法国数学家(1717—1783)在1747年指出,如果按照多项式的四则运算规则对虚数进行运算,那么它的结果总是的形式(a、b都是实数)(说明:现行教科书中没有使用记号=-i,而使用=一1)。法国数学家棣莫佛(1667—1754)在1730年发现公式了,这就是著名的棣莫佛定理。
欧拉在1748年发现了有名的关系式,并且是他在《微分公式(1777年)一文中第一次用i来表示一1的平方根,首创了用符号i作为虚数的单位。“虚数”实际上不是想象出来的,而它是确实存在的。
返回
挪威的测量学家成塞尔(1745—1818)在1779年试图给于这种虚数以直观的几何解释,并首先发表其作法,然而没有得到学术界的重视。
德国数学家阿甘得(1777—1855)在1806年公布了虚数的图象表示法,即所有实数能用一条数轴表示,同样,虚数也能用一个平面上的点来表示。在直角坐标系中,横轴上取对应实数a的点A,纵轴上取对应实数b的点B,并过这两点引平行于坐标轴的直线,它们的交点C就表示复数a+bi。象这样,由各点都对应复数的平面叫做“复平面”,后来又称“阿甘得平面”。
高斯在1831年,用实数组(a,b)代表复数a+bi,并建立了复数的某些运算,使得复数的某些运算也象实数一样地“代数化”。他又在1832年第一次提出了“复数”这个名词,还将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合。统一于表示同一复数的代数式和三角式两种形式中,并把数轴上的点与实数—一对应,扩展为平面上的点与复数—一对应。高斯不仅把复数看作平面上的点,而且还看作是一种向量,并利用复数与向量之间—一对应的关系,阐述了复数的几何加法与乘法。至此,复数理论才比较完整和系统地建立起来了。
返回
经过许多数学家长期不懈的努力,深刻探讨并发展了复数理论,才使得在数学领域游荡了200年的幽灵——虚数揭去了神秘的面纱,显现出它的本来面目,原来虚数不虚呵。虚数成为了数系大家庭中一员,从而实数集才扩充到了复数集。
随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且为证明机翼上升力的基本定理起到了重要作用,并在解决堤坝渗水的问题中显示了它的威力,也为建立巨大水电站提供了重要的理论依据。
返回
毕达哥拉斯是公元前五世纪古希腊的著名数学家与哲学家。他曾创立了一个合政治、学术、宗教三位一体的神秘主义派别:毕达哥拉斯学派。由毕达哥拉斯提出的著名命题“万物皆数”是该学派的哲学基石。而“一切数均可表成整数或整数之比”则是这一学派的数学信仰。他们重视自然及社会中不变因素的研究,把几何、算术、天文学、音乐称为“四艺”,在其中追求宇宙的和谐及规律性。
毕达哥拉斯
在国外,最早给出这一定理证明的是古希腊的毕达哥拉斯。因而国外一般称之为“毕达哥拉斯定理”。并且据说毕达哥拉斯在完成这一定理证明后欣喜若狂,而杀牛百只以示庆贺。因此这一定理还又获得了一个带神秘色彩的称号:“百牛定理”。
勾股定理是欧氏几何中最著名的定理之一。天文学家开普勒曾称其为欧氏几何两颗璀璨的明珠之一。它在数学与人类的实践活动中有着极其广泛的应用,同时也是人类最早认识到的平面几何定理之一。在我国,最早的一部天文数学著作《周髀算经》中就已有了关于这一定理的初步认识。不过,在我国对于勾股定理的证明却是较迟的事情。一直到三国时期的赵爽才用面积割补给出它的第一种证明。
资料2
第一次数学危机与无理数的产生
返回
毕达哥拉斯是公元前五世纪古希腊的著名数学家与哲学家。他曾创立了一个合政治、学术、宗教三位一体的神秘主义派别:毕达哥拉斯学派。由毕达哥拉斯提出的著名命题“万物皆数”是该学派的哲学基石。而“一切数均可表成整数或整数之比”则是这一学派的数学信仰。他们重视自然及社会中不变因素的研究,把几何、算术、天文学、音乐称为“四艺”,在其中追求宇宙的和谐及规律性。
然而,具有戏剧性的是由毕达哥拉斯建立的毕达哥拉斯定理却成了毕达哥拉斯学派数学信仰的“掘墓人”。
毕达哥拉斯定理提出后,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线长度是多少呢?他发现这一长度既不能用整数,也不能用分数表示,而只能用一个新数来表示。
希帕索斯的发现导致了数学史上第一个无理数√2
的诞生。小小√2的出现,却在当时的数学界掀起了一场巨大风暴。它直接动摇了毕达哥拉斯学派的数学信仰,使毕达哥拉斯学派为之大为恐慌。为此,希帕索斯的同伴把他抛进大海。不过更有可能是毕达哥拉斯知道了事实,而希帕索斯因泄密而被处死。
返回
这一伟大发现不但是对毕达哥拉斯学派的致命打击。对于当时所有古希腊人的观念这都是一个极大的冲击。这一结论的悖论性表现在它与常识的冲突上:任何量,在任何精确度的范围内都可以表示成有理数。这不但在希腊当时是人们普遍接受的信仰,就是在今天,测量技术已经高度发展时,这个断言也毫无例外是正确的!可是为我们的经验所确信的,完全符合常识的论断居然被小小的√2的存在而推翻了!更糟糕的是,面对这一荒谬人们竟然毫无办法。这就在当时直接导致了人们认识上的危机,从而导致了西方数学史上一场大的风波,史称“第一次数学危机”。
二百年后,大约在公元前370年,才华横溢的欧多克索斯建立起一套完整的比例论。他本人的著作已失传,他的成果被保存在欧几里德《几何原本》一书第五篇中。欧多克索斯的巧妙方法可以避开无理数这一“逻辑上的丑闻”,并保留住与之相关的一些结论,从而解决了由无理数出现而引起的数学危机。
欧多克索斯
返回
但欧多克索斯的解决方式,是借助几何方法,通过避免直接出现无理数而实现的。这就生硬地把数和量肢解开来。在这种解决方案下,对无理数的使用只有在几何中是允许的,合法的,在代数中就是非法的,不合逻辑的。或者说无理数只被当作是附在几何量上的单纯符号,而不被当作真正的数。一直到18世纪,当数学家证明了基本常数如圆周率是无理数时,拥护无理数存在的人才多起来。
到十九世纪下半叶,现在意义上的实数理论建立起来后,无理数本质被彻底搞清,无理数在数学园地中才真正扎下了根。无理数在数学中合法地位的确立,一方面使人类对数的认识从有理数拓展到实数,另一方面也真正彻底、圆满地解决了第一次数学危机。
返回
7.1
复数的概念
7.1.1
数系的扩充和复数的概念
课标对本节的要求:
1.了解复数的概念:
能类比有有理数系扩充到实数系的过程和方法,通过方程的解,认识复数;
2.理解复数:
能描述复数代数式表示结构特征,能判断复数的实部、虚部;知道复数集,实数集,虚数集,纯虚数集的关系;
3.理解复数相等:
能说明复数相等的含义,会判断复数相等。
我们知道,对于实系数一元二次方程ax2+bx+c=0,当?=b2-4ac
例如,方程x3-15x+4=0
用求根公式法可得以下三个根:
而用因式分解法又可得(x-4)(x2+4x+1)=0,此时三个根为:
本章及本节的引入
要解决这个问题的过程中,就必须排除许多困扰,如负实数能不能开平方?如何开方?负实数开平方的意义是什么?等等
。
本章我们就开学习相关的一些简单知识,感受引引入复数的必要性,了解复数系的扩充过程和方法,研究复数的表示、运算及其几何意义,体会数形的融合。
你能回想起数系的扩展过程吗?
在从自然数集扩充到实数集的过程中,每次引入新数后,原有的加法和乘法的运算律都没有变。
从社会实践来看,数的扩充都是为了解决生产生活中的问题,数集的每一次扩充,都是在原数集的基础上添加新数得到的。
因此,在解决判别式小于0实系数一元二次方程时,一个自然的想法就是引入一个新数,把原有的实数集进行扩充,从而使方程变得可解。复数的引入就与这种想法直接相关。
问题1:从方程的角度看,负实数能不能开平方的问题可以归结为方程“x2+a=0”(其中a>0)有没有解的问题,从而进一步归结为方程“x2+1=0”有没有解的问题。这是为什么?
当a>0时,-a<0
”实数-a能不能开平方”的问题,就是“-a有没有平方根”的问题。
而根据平方根的定义,就是“是否存在一个数x使x2=-a”,即”方程x2+a=0(其中a>0)有没有解”的问题。
因此
”方程x2+a=0(其中a>0)有没有解”的问题,可最终归结为“x2+1=0”有没有解的问题。
探究新知
问题2:从我们知道,方程x2+1=0在实数集是无解的,联系到自然数集到实数集的扩充过程,是否能引入新数,将实数集适当地进一步扩充,使这个方程在这个新的数集中有解的?
1637年,法国数学家笛卡尔,在《几何学》给出“虚数”这一名称,使“虚的数”与“实的数”相对应,从此,虚数才流传开来。
1748年,瑞典数学家欧拉在发现了著名的关系式(欧拉公式)。
1777年,欧拉在《微分公式》一文中第一次用”i“来表示”-1的平方根“,首创了用符号”i“作为虚数的单位。
添加新数i后,你最希望这个有什么运算性质?
i
可以与实数之间进行加法和乘法运算,并希望实数原有的关于加法和乘的运算律仍然成立.
虚数
虚数单位i
数
i
叫做虚数单位,并规定:
(1)它的平方等于
-1,即
(2)i
可以与实数进行加法和乘法运算,且实数原有的有关加法和乘法的运算律仍然成立.
问题3:实数系经过扩充以后,按照以上的(2),这个新数系会由哪些数来组成呢?
你能写出类似于以上数的形式吗?说说理由。
出现新数喽!
复数的概念
形如
a+bi
(a,b∈R)
的数叫做复数,其中i是虚数单位。复数一般用字母z来表示。
全体复数所成的集合叫做复数集,复数集一般用字母C表示,即
a:实部
b:虚部
思考:数系是如何扩展到复数系的?你能对复数进行分类吗?
复数的分类
实数
虚数
纯虚数
非纯虚数
(a∈R,b∈R)
纯虚数集
引入虚数后,实数原有的加法和乘法的运算律仍然成立。
例1.写出下列复数的实部和虚部,并指出哪些是实数,哪些是虚数,哪些是纯虚数?
例析
解:
两个复数相等的充要条件是它们的实部和虚部分别相等。即
说明:
(1)两个复数一般不能比较大小(除非两个均为实数)
(2)复数相等定义的作用:
1)判断两个复数是否相等;
2)求某些复数值。利用实部和虚部分别相等转化成方程(组),通过解方程(组),求出复数。
复数相等
例2.实数m取什么值时,复数
z=m+1+(m-1)i
是下列数?
(1)实数?
(2)虚数?
(3)纯虚数?
(1)由m-1=0得,m=1
∴当
m=1时,z为实数。
(2)由m-1≠0得,m≠1
∴当
m≠1时,z为虚数。
(3)由题意得
解得m=-1
∴当
m=-1时,z为纯虚数
例析
解:
例3.已知(x+y)+(x-2y)i=(2x-5)+(3x+y)i,其中x,y∈R,求x,y.
由复数相等的定义得
解得
解:
1.求满足下列条件的实数x,y的值:
(1)(x+y)+(y-1)i=(2x+3y)+(2y+1)i
(2)(x+y-3)+(x-2)i=0
练习
解:(1)由复数相等的定义得
解得
(2)由复数相等的定义得
解得
2.当m为何实数时,复数z=(m2+m-2)+(m2-1)i
是
(1)实数?
(2)虚数
?
(3)纯虚数?
4.复数相等的含义.
复数,复数的实部
、虚部
3.复数的分类;
1.虚数单位i的引入和数系扩充;
2.复数的基本概念;
小结
阅读资料
作业
教材P73习题第1,2,3题
16世纪意大利米兰学者(Jerome
Cardan1501—1576)在1545年发表的《重要的艺术》一书中,公布了三次方程的一般解法,被后人称之为“卡当公式”。他是第一个把负数的平方根写到公式中的数学家,并且在讨论是否可能把10分成两部分,使它们的乘积等于40时,他把答案写成
,尽管他认为和这两个表示式是没有意义的、想象的、虚无飘渺的,但他还是把10分成了两部分,并使它们的乘积等于40。
给出“虚数”这一名称的是法国数学家笛卡尔(1596—1650),他在《几何学》(1637年发表)中使“虚的数”与“实的数”相对应,从此,虚数才流传开来。
数系中发现一颗新星——虚数,于是引起了数学界的一片困惑,很多大数学家都不承认虚数。
德国数学家(1646—1716)在1702年说:“虚数是神灵遁迹的精微而奇异的隐避所,它大概是存在和虚妄两界中的两栖物”。
复数的起源
资料1
返回
瑞士数学大师(1707—1783)说;“一切形如i的式子都是不可能有的,它是想象的数,因为它们所表示的是负数的平方根。对于这类数,我们只能断言,它们既不是什么都不是,也不比什么都不是多些什么,更不比什么都不是少些什么,它们纯属虚幻。”
然而,真理性的东西一定可以经得住时间和空间的考验,最终占有自己的一席之地。
法国数学家(1717—1783)在1747年指出,如果按照多项式的四则运算规则对虚数进行运算,那么它的结果总是的形式(a、b都是实数)(说明:现行教科书中没有使用记号=-i,而使用=一1)。法国数学家棣莫佛(1667—1754)在1730年发现公式了,这就是著名的棣莫佛定理。
欧拉在1748年发现了有名的关系式,并且是他在《微分公式(1777年)一文中第一次用i来表示一1的平方根,首创了用符号i作为虚数的单位。“虚数”实际上不是想象出来的,而它是确实存在的。
返回
挪威的测量学家成塞尔(1745—1818)在1779年试图给于这种虚数以直观的几何解释,并首先发表其作法,然而没有得到学术界的重视。
德国数学家阿甘得(1777—1855)在1806年公布了虚数的图象表示法,即所有实数能用一条数轴表示,同样,虚数也能用一个平面上的点来表示。在直角坐标系中,横轴上取对应实数a的点A,纵轴上取对应实数b的点B,并过这两点引平行于坐标轴的直线,它们的交点C就表示复数a+bi。象这样,由各点都对应复数的平面叫做“复平面”,后来又称“阿甘得平面”。
高斯在1831年,用实数组(a,b)代表复数a+bi,并建立了复数的某些运算,使得复数的某些运算也象实数一样地“代数化”。他又在1832年第一次提出了“复数”这个名词,还将表示平面上同一点的两种不同方法——直角坐标法和极坐标法加以综合。统一于表示同一复数的代数式和三角式两种形式中,并把数轴上的点与实数—一对应,扩展为平面上的点与复数—一对应。高斯不仅把复数看作平面上的点,而且还看作是一种向量,并利用复数与向量之间—一对应的关系,阐述了复数的几何加法与乘法。至此,复数理论才比较完整和系统地建立起来了。
返回
经过许多数学家长期不懈的努力,深刻探讨并发展了复数理论,才使得在数学领域游荡了200年的幽灵——虚数揭去了神秘的面纱,显现出它的本来面目,原来虚数不虚呵。虚数成为了数系大家庭中一员,从而实数集才扩充到了复数集。
随着科学和技术的进步,复数理论已越来越显出它的重要性,它不但对于数学本身的发展有着极其重要的意义,而且为证明机翼上升力的基本定理起到了重要作用,并在解决堤坝渗水的问题中显示了它的威力,也为建立巨大水电站提供了重要的理论依据。
返回
毕达哥拉斯是公元前五世纪古希腊的著名数学家与哲学家。他曾创立了一个合政治、学术、宗教三位一体的神秘主义派别:毕达哥拉斯学派。由毕达哥拉斯提出的著名命题“万物皆数”是该学派的哲学基石。而“一切数均可表成整数或整数之比”则是这一学派的数学信仰。他们重视自然及社会中不变因素的研究,把几何、算术、天文学、音乐称为“四艺”,在其中追求宇宙的和谐及规律性。
毕达哥拉斯
在国外,最早给出这一定理证明的是古希腊的毕达哥拉斯。因而国外一般称之为“毕达哥拉斯定理”。并且据说毕达哥拉斯在完成这一定理证明后欣喜若狂,而杀牛百只以示庆贺。因此这一定理还又获得了一个带神秘色彩的称号:“百牛定理”。
勾股定理是欧氏几何中最著名的定理之一。天文学家开普勒曾称其为欧氏几何两颗璀璨的明珠之一。它在数学与人类的实践活动中有着极其广泛的应用,同时也是人类最早认识到的平面几何定理之一。在我国,最早的一部天文数学著作《周髀算经》中就已有了关于这一定理的初步认识。不过,在我国对于勾股定理的证明却是较迟的事情。一直到三国时期的赵爽才用面积割补给出它的第一种证明。
资料2
第一次数学危机与无理数的产生
返回
毕达哥拉斯是公元前五世纪古希腊的著名数学家与哲学家。他曾创立了一个合政治、学术、宗教三位一体的神秘主义派别:毕达哥拉斯学派。由毕达哥拉斯提出的著名命题“万物皆数”是该学派的哲学基石。而“一切数均可表成整数或整数之比”则是这一学派的数学信仰。他们重视自然及社会中不变因素的研究,把几何、算术、天文学、音乐称为“四艺”,在其中追求宇宙的和谐及规律性。
然而,具有戏剧性的是由毕达哥拉斯建立的毕达哥拉斯定理却成了毕达哥拉斯学派数学信仰的“掘墓人”。
毕达哥拉斯定理提出后,其学派中的一个成员希帕索斯考虑了一个问题:边长为1的正方形其对角线长度是多少呢?他发现这一长度既不能用整数,也不能用分数表示,而只能用一个新数来表示。
希帕索斯的发现导致了数学史上第一个无理数√2
的诞生。小小√2的出现,却在当时的数学界掀起了一场巨大风暴。它直接动摇了毕达哥拉斯学派的数学信仰,使毕达哥拉斯学派为之大为恐慌。为此,希帕索斯的同伴把他抛进大海。不过更有可能是毕达哥拉斯知道了事实,而希帕索斯因泄密而被处死。
返回
这一伟大发现不但是对毕达哥拉斯学派的致命打击。对于当时所有古希腊人的观念这都是一个极大的冲击。这一结论的悖论性表现在它与常识的冲突上:任何量,在任何精确度的范围内都可以表示成有理数。这不但在希腊当时是人们普遍接受的信仰,就是在今天,测量技术已经高度发展时,这个断言也毫无例外是正确的!可是为我们的经验所确信的,完全符合常识的论断居然被小小的√2的存在而推翻了!更糟糕的是,面对这一荒谬人们竟然毫无办法。这就在当时直接导致了人们认识上的危机,从而导致了西方数学史上一场大的风波,史称“第一次数学危机”。
二百年后,大约在公元前370年,才华横溢的欧多克索斯建立起一套完整的比例论。他本人的著作已失传,他的成果被保存在欧几里德《几何原本》一书第五篇中。欧多克索斯的巧妙方法可以避开无理数这一“逻辑上的丑闻”,并保留住与之相关的一些结论,从而解决了由无理数出现而引起的数学危机。
欧多克索斯
返回
但欧多克索斯的解决方式,是借助几何方法,通过避免直接出现无理数而实现的。这就生硬地把数和量肢解开来。在这种解决方案下,对无理数的使用只有在几何中是允许的,合法的,在代数中就是非法的,不合逻辑的。或者说无理数只被当作是附在几何量上的单纯符号,而不被当作真正的数。一直到18世纪,当数学家证明了基本常数如圆周率是无理数时,拥护无理数存在的人才多起来。
到十九世纪下半叶,现在意义上的实数理论建立起来后,无理数本质被彻底搞清,无理数在数学园地中才真正扎下了根。无理数在数学中合法地位的确立,一方面使人类对数的认识从有理数拓展到实数,另一方面也真正彻底、圆满地解决了第一次数学危机。
返回
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
