10.3频率与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(机构专用)
文档属性
| 名称 | 10.3频率与概率-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步讲义(机构专用) |

|
|
| 格式 | doc | ||
| 文件大小 | 730.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览



文档简介
10.3 频率与概率
在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性。一般地,随着试验次数n的增大,频率偏高概率的幅度会缩小,即事件A发生的频率会逐渐稳定与事件A发生的概率P(A),我们称频率的这个性质为频率的稳定性。因此,我们可以用频率估计概率P(A)
题型一 频率与概率
例 1 下列叙述随机事件的频率与概率的关系中,说法正确的是( )
A.频率就是概率 B.频率是随机的,与试验次数无关
C.概率是稳定的,与试验次数无关 D.概率是随机的,与试验次数有关
【答案】C
【分析】
根据频率、概率的概念,可得结果.
【详解】
频率指的是:在相同条件下重复试验下,
事件A出现的次数除以总数,是变化的
概率指的是: 在大量重复进行同一个实验时,
事件A发生的频率总接近于某个常数,
这个常数就是事件A的概率,是不变的
故选:C
下列关于概率的说法正确的是( )
A.频率就是概率
B.任何事件的概率都是在(0,1)之间
C.概率是客观存在的,与试验次数无关
D.概率是随机的,与试验次数有关
【答案】C
【分析】
根据频率与概率的定义一一进行判断可得答案.
【详解】
解:事件A的频率是指事件A发生的频数与n次事件中事件A出现的次数比,
一般来说,随机事件A在每次实验中是否发生时不能预料的,但在大量重复的实验后,随着实验次数的增加,事件A发生的频率会逐渐稳定在区间的某个常数上,这个常数就是事件A的概率,故可得:概率是客观存在的,与试验次数无关,
故选:C.
题型二 用频率估计概率
例 2 一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20000辆汽车的信息,时间是从某年的5月1日到下一年的4月30日,发现共有600辆汽车的挡风玻璃破碎,则一辆汽车在一年内挡风玻璃破碎的概率近似为_______.
【答案】
【分析】
因为实验次数较大,可用频率估计概率,根据频率的计算公式,即可求得答案.
【详解】
实验次数较大,可用频率估计概率
概率.
故答案为:.
某篮球运动员在同一条件下进行投篮练习,结果如下表所示.
投篮次数n/次 8 10 15 20 30 40 50
进球次数m/次 6 8 12 17 25 32 38
进球频率
(1)填写上表中的进球频率;
(2)这位运动员投篮一次,进球的概率大约是多少?
【答案】(1)见解析;(2)0.8
【解析】
试题分析:(1)由题意可得:频率,即,算出数据.(2)在同一条件是进行大量试验,频率会稳定在一个常数附近,我们就用这个常数做为概率的估计值.
试题解析;(1)表中从左到右依次填:0.75 0.8 0.8 0.85 0.83 0.8 0.76.
(2)由于进球频率都在0.8左右摆动,故这位运动员投篮一次,进球的概率约是0.8.
题型三 随机模拟
例 3 用随机模拟方法得到的频率( )
A.大于概率 B.小于概率 C.等于概率 D.是概率的近似值
【答案】D
【分析】
根据频率和概率的定义,当实验数据越多频率就越接近概率,即可求得答案.
【详解】
当实验数据越多频率就越接近概率
用随机模拟方法得到的频率,数据是有限的,是接近概率.
故选:D.
用随机模拟方法求得某几何概型的概率为m,其实际概率的大小为n,则( )
A.m>n B.mC.m=n D.m是n的近似值
【答案】D
【解析】随机摸拟法求其概率,只是对概率的估计.
题型四 实际应用
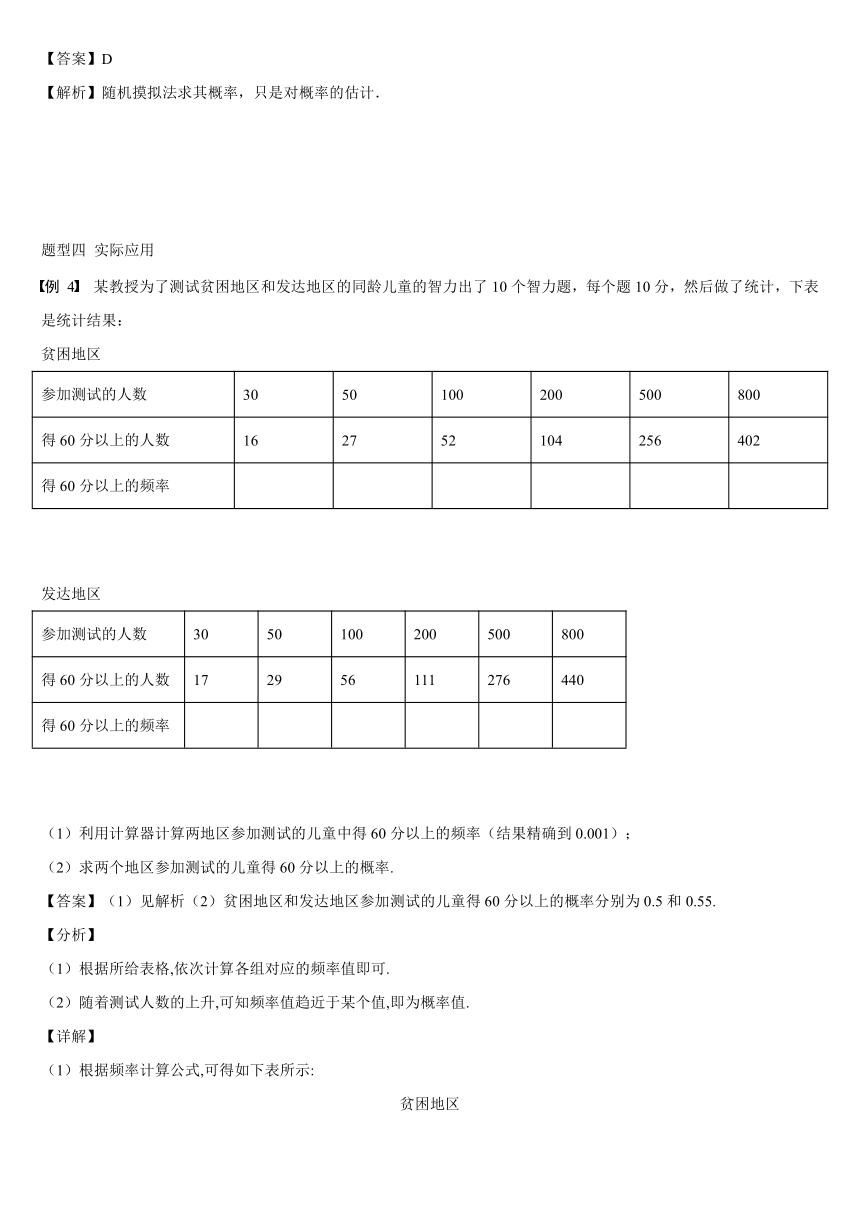
例 4 某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,下表是统计结果:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率
(1)利用计算器计算两地区参加测试的儿童中得60分以上的频率(结果精确到0.001);
(2)求两个地区参加测试的儿童得60分以上的概率.
【答案】(1)见解析(2)贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
【分析】
(1)根据所给表格,依次计算各组对应的频率值即可.
(2)随着测试人数的上升,可知频率值趋近于某个值,即为概率值.
【详解】
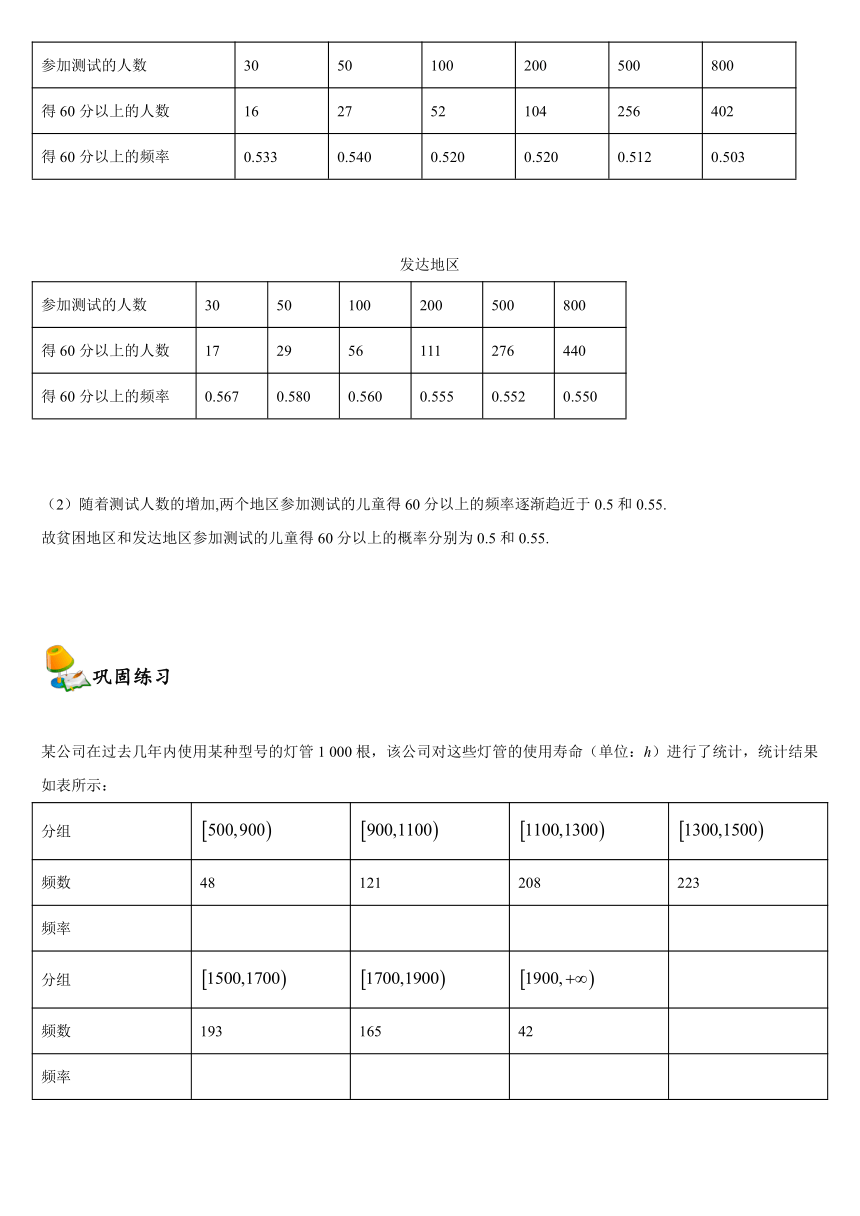
(1)根据频率计算公式,可得如下表所示:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率 0.533 0.540 0.520 0.520 0.512 0.503
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率 0.567 0.580 0.560 0.555 0.552 0.550
(2)随着测试人数的增加,两个地区参加测试的儿童得60分以上的频率逐渐趋近于0.5和0.55.
故贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
某公司在过去几年内使用某种型号的灯管1 000根,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表所示:
分组
频数 48 121 208 223
频率
分组
频数 193 165 42
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计该种型号灯管的使用寿命不足1500 h的概率.
【答案】(1)见解析;(2)0.6.
【分析】
(1)根据公式,填写表格;
(2)首先计算样本中寿命不足1500 h的频数,再用频率估算概率.
【详解】
(1);(2)0.6.
分组
频数 48 121 208 223
频率 0.048 0.121 0.208 0.223
分组
频数 193 165 42
频率 0.193 0.165 0.042
(2)样本中寿命不足1500 h的频数是,所以样本中寿命不足1500 h的频率是,即该种型号灯管的使用寿命不足1500 h的概率约为0.6.
1、某班学生在一次数学考试中的成绩分布如表
分数段
人数 2 5 6 8 12 6 4 2
那么分数在中的频率约是(精确到0.01)( )
A.0.18 B.0.47 C.0.50 D.0.38
【答案】A
【分析】
根据成绩分布表,先求得总人数,即可求得分数在中的频率.
【详解】
某班总人数,
成绩在中的有8人,其频率为.
故选:A
2、用随机模拟方法估计概率时,其准确程度决定于( )
A.产生的随机数的大小 B.产生的随机数的个数
C.随机数对应的结果 D.产生随机数的方法
【答案】B
【解析】
随机数容量越大,概率越接近实际数.
3、(多选)给出下列四个命题,其中正确的命题有( )
A.做100次抛硬币的试验,结果51次出现正面朝上,因此,出现正直朝上的概率是
B.随机事件发生的频率就是这个随机事件发生的概率
C.抛掷骰子100次,得点数是1的结果有18次,则出现1点的频率是
D.随机事件发生的频率不一定是这个随机事件发生的概率
【答案】CD
【分析】
根据概率和频率定义,逐项判断,即可求得答案.
【详解】
对于A,混淆了频率与概率的区别,故A错误;
对于B,混淆了频率与概率的区别,故B错误;
对于C,抛掷骰子次,得点数是的结果有次,则出现点的频率是,符合频率定义,故C正确;
对于D,频率是概率的估计值,故D正确.
故选:CD.
4、下列命题中不正确的是( )
A.根据古典概型概率计算公式求出的值是事件A发生的概率的精确值
B.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数,得到的值是的近似值
C.频率是随机的,在试验前不能确定,随着试验次数的增加,频率会越来越接近概率
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可性相同
【答案】C
【分析】
根据概率的定义以及古典概型概率计算方法逐个选项判断即可.
【详解】
对于A,即古典概型概率计算公式,很明显正确的;
对于B,随机模拟中得到的值是概率的近似值,则B项命题正确;
对于C,频率稳定在某个常数上,这个常数叫做概率,但与概率的趋近程度不是试验次数的函数,C命题不正确;
对于D,5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性都是,D命题正确;
故选:C.
5、某养鸡厂用鸡蛋孵化小鸡,用200个鸡蛋孵化出170只小鸡,由此估计,要孵化出2500只小鸡,大约需要鸡蛋的个数为( )
A.3022 B.2941 C.2800 D.3125
【答案】B
【分析】
根据样本的数据来估计要孵化出2500只小鸡,大约需要鸡蛋的个数.
【详解】
解:设大约需要个鸡蛋,则解得
故选:
【点睛】
本题古典概型的概率计算以及概率的应用,属于基础题.
6、下列说法:
①频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小;
②百分率是频率,但不是概率;
③频率是不能脱离试验次数的实验值,而概率是具有确定性的不依赖于试验次数的理论值;
④频率是概率的近似值,概率是频率的稳定值.
其中正确的是______________.
【答案】①③④
【分析】
根据频率与概率的概念与区别,依次判断各选项即可.
【详解】
对于①,由频率和概率概念: 频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小.可知①正确;
对于②,概率也可以用百分率表示,故②错误.
对于③,频率与试验次数相关,而概率与试验次数无关,所以③正确;
对于④,对于不同批次的试验,频率不一定相同,但概率相同,因而频率是概率的近似值,概率是频率的稳定值,所以④正确.
由概率和频率的定义中可知①③④正确.
故答案为: ①③④
7、某水产试验厂进行某种鱼卵的人工孵化,6个试验小组记录了不同的鱼卵数所孵化出的鱼苗数,如下表所示:
鱼卵数 200 600 900 1200 1800 2400
孵化出的鱼苗数 188 548 817 1067 1614 2163
孵化成功的频率 0.940 0.913 0.908 ① 0.897 ②
(1)表中①②对应的频率分别为多少(结果保留三位小数)?
(2)估计这种鱼卵孵化成功的概率.
(3)要孵化5000尾鱼苗,大概需要鱼卵多少个(精确到百位)?
【答案】(1)(2)0.9(3)
【分析】
(1)计算的值,即可得答案;
(2)从表中数据可看出,虽然频率都不一样,但随着试验的鱼卵数不断增多,孵化成功的频率稳定在0.9附近,即可得答案;
(3)利用频率等于频数除以总数计算,即可得答案.
【详解】
(1),所以①②对应的频率分别为.
(2)从表中数据可看出,虽然频率都不一样,但随着试验的鱼卵数不断增多,孵化成功的频率稳定在0.9附近,由此可估计该种鱼卵孵化成功的概率为0.9.
(3)大概需要鱼卵(个).
8、某市统计近几年婴儿出生数及其中男婴数(单位:人)如下:
出生婴儿数 21840 23070 20094 19982
出生男婴数 11453 12031 10297 10242
(1)试计算这几年男婴出生的频率(精确到0.001);
(2)估计该男婴出生的概率(精确到0.1).
【答案】(1),,,(2)0.5
【分析】
(1)根据所给数表,可依次计算出这几年男婴出生的频率;
(2)由频率估计概率,即可得解.
【详解】
(1)由表格可知,男婴出生的概率分别为
,
,
,
.
(2)由(1)中频率可估计该市男婴出生的概率为0.5.
在任何确定次数的随机试验中,一个随机事件A发生的频率具有随机性。一般地,随着试验次数n的增大,频率偏高概率的幅度会缩小,即事件A发生的频率会逐渐稳定与事件A发生的概率P(A),我们称频率的这个性质为频率的稳定性。因此,我们可以用频率估计概率P(A)
题型一 频率与概率
例 1 下列叙述随机事件的频率与概率的关系中,说法正确的是( )
A.频率就是概率 B.频率是随机的,与试验次数无关
C.概率是稳定的,与试验次数无关 D.概率是随机的,与试验次数有关
【答案】C
【分析】
根据频率、概率的概念,可得结果.
【详解】
频率指的是:在相同条件下重复试验下,
事件A出现的次数除以总数,是变化的
概率指的是: 在大量重复进行同一个实验时,
事件A发生的频率总接近于某个常数,
这个常数就是事件A的概率,是不变的
故选:C
下列关于概率的说法正确的是( )
A.频率就是概率
B.任何事件的概率都是在(0,1)之间
C.概率是客观存在的,与试验次数无关
D.概率是随机的,与试验次数有关
【答案】C
【分析】
根据频率与概率的定义一一进行判断可得答案.
【详解】
解:事件A的频率是指事件A发生的频数与n次事件中事件A出现的次数比,
一般来说,随机事件A在每次实验中是否发生时不能预料的,但在大量重复的实验后,随着实验次数的增加,事件A发生的频率会逐渐稳定在区间的某个常数上,这个常数就是事件A的概率,故可得:概率是客观存在的,与试验次数无关,
故选:C.
题型二 用频率估计概率
例 2 一家保险公司想了解汽车的挡风玻璃破碎的概率,公司收集了20000辆汽车的信息,时间是从某年的5月1日到下一年的4月30日,发现共有600辆汽车的挡风玻璃破碎,则一辆汽车在一年内挡风玻璃破碎的概率近似为_______.
【答案】
【分析】
因为实验次数较大,可用频率估计概率,根据频率的计算公式,即可求得答案.
【详解】
实验次数较大,可用频率估计概率
概率.
故答案为:.
某篮球运动员在同一条件下进行投篮练习,结果如下表所示.
投篮次数n/次 8 10 15 20 30 40 50
进球次数m/次 6 8 12 17 25 32 38
进球频率
(1)填写上表中的进球频率;
(2)这位运动员投篮一次,进球的概率大约是多少?
【答案】(1)见解析;(2)0.8
【解析】
试题分析:(1)由题意可得:频率,即,算出数据.(2)在同一条件是进行大量试验,频率会稳定在一个常数附近,我们就用这个常数做为概率的估计值.
试题解析;(1)表中从左到右依次填:0.75 0.8 0.8 0.85 0.83 0.8 0.76.
(2)由于进球频率都在0.8左右摆动,故这位运动员投篮一次,进球的概率约是0.8.
题型三 随机模拟
例 3 用随机模拟方法得到的频率( )
A.大于概率 B.小于概率 C.等于概率 D.是概率的近似值
【答案】D
【分析】
根据频率和概率的定义,当实验数据越多频率就越接近概率,即可求得答案.
【详解】
当实验数据越多频率就越接近概率
用随机模拟方法得到的频率,数据是有限的,是接近概率.
故选:D.
用随机模拟方法求得某几何概型的概率为m,其实际概率的大小为n,则( )
A.m>n B.m
【答案】D
【解析】随机摸拟法求其概率,只是对概率的估计.
题型四 实际应用
例 4 某教授为了测试贫困地区和发达地区的同龄儿童的智力出了10个智力题,每个题10分,然后做了统计,下表是统计结果:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率
(1)利用计算器计算两地区参加测试的儿童中得60分以上的频率(结果精确到0.001);
(2)求两个地区参加测试的儿童得60分以上的概率.
【答案】(1)见解析(2)贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
【分析】
(1)根据所给表格,依次计算各组对应的频率值即可.
(2)随着测试人数的上升,可知频率值趋近于某个值,即为概率值.
【详解】
(1)根据频率计算公式,可得如下表所示:
贫困地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 16 27 52 104 256 402
得60分以上的频率 0.533 0.540 0.520 0.520 0.512 0.503
发达地区
参加测试的人数 30 50 100 200 500 800
得60分以上的人数 17 29 56 111 276 440
得60分以上的频率 0.567 0.580 0.560 0.555 0.552 0.550
(2)随着测试人数的增加,两个地区参加测试的儿童得60分以上的频率逐渐趋近于0.5和0.55.
故贫困地区和发达地区参加测试的儿童得60分以上的概率分别为0.5和0.55.
某公司在过去几年内使用某种型号的灯管1 000根,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如表所示:
分组
频数 48 121 208 223
频率
分组
频数 193 165 42
频率
(1)将各组的频率填入表中;
(2)根据上述统计结果,估计该种型号灯管的使用寿命不足1500 h的概率.
【答案】(1)见解析;(2)0.6.
【分析】
(1)根据公式,填写表格;
(2)首先计算样本中寿命不足1500 h的频数,再用频率估算概率.
【详解】
(1);(2)0.6.
分组
频数 48 121 208 223
频率 0.048 0.121 0.208 0.223
分组
频数 193 165 42
频率 0.193 0.165 0.042
(2)样本中寿命不足1500 h的频数是,所以样本中寿命不足1500 h的频率是,即该种型号灯管的使用寿命不足1500 h的概率约为0.6.
1、某班学生在一次数学考试中的成绩分布如表
分数段
人数 2 5 6 8 12 6 4 2
那么分数在中的频率约是(精确到0.01)( )
A.0.18 B.0.47 C.0.50 D.0.38
【答案】A
【分析】
根据成绩分布表,先求得总人数,即可求得分数在中的频率.
【详解】
某班总人数,
成绩在中的有8人,其频率为.
故选:A
2、用随机模拟方法估计概率时,其准确程度决定于( )
A.产生的随机数的大小 B.产生的随机数的个数
C.随机数对应的结果 D.产生随机数的方法
【答案】B
【解析】
随机数容量越大,概率越接近实际数.
3、(多选)给出下列四个命题,其中正确的命题有( )
A.做100次抛硬币的试验,结果51次出现正面朝上,因此,出现正直朝上的概率是
B.随机事件发生的频率就是这个随机事件发生的概率
C.抛掷骰子100次,得点数是1的结果有18次,则出现1点的频率是
D.随机事件发生的频率不一定是这个随机事件发生的概率
【答案】CD
【分析】
根据概率和频率定义,逐项判断,即可求得答案.
【详解】
对于A,混淆了频率与概率的区别,故A错误;
对于B,混淆了频率与概率的区别,故B错误;
对于C,抛掷骰子次,得点数是的结果有次,则出现点的频率是,符合频率定义,故C正确;
对于D,频率是概率的估计值,故D正确.
故选:CD.
4、下列命题中不正确的是( )
A.根据古典概型概率计算公式求出的值是事件A发生的概率的精确值
B.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数,得到的值是的近似值
C.频率是随机的,在试验前不能确定,随着试验次数的增加,频率会越来越接近概率
D.5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可性相同
【答案】C
【分析】
根据概率的定义以及古典概型概率计算方法逐个选项判断即可.
【详解】
对于A,即古典概型概率计算公式,很明显正确的;
对于B,随机模拟中得到的值是概率的近似值,则B项命题正确;
对于C,频率稳定在某个常数上,这个常数叫做概率,但与概率的趋近程度不是试验次数的函数,C命题不正确;
对于D,5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性都是,D命题正确;
故选:C.
5、某养鸡厂用鸡蛋孵化小鸡,用200个鸡蛋孵化出170只小鸡,由此估计,要孵化出2500只小鸡,大约需要鸡蛋的个数为( )
A.3022 B.2941 C.2800 D.3125
【答案】B
【分析】
根据样本的数据来估计要孵化出2500只小鸡,大约需要鸡蛋的个数.
【详解】
解:设大约需要个鸡蛋,则解得
故选:
【点睛】
本题古典概型的概率计算以及概率的应用,属于基础题.
6、下列说法:
①频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小;
②百分率是频率,但不是概率;
③频率是不能脱离试验次数的实验值,而概率是具有确定性的不依赖于试验次数的理论值;
④频率是概率的近似值,概率是频率的稳定值.
其中正确的是______________.
【答案】①③④
【分析】
根据频率与概率的概念与区别,依次判断各选项即可.
【详解】
对于①,由频率和概率概念: 频率是反映事件发生的频繁程度,概率是反映事件发生的可能性大小.可知①正确;
对于②,概率也可以用百分率表示,故②错误.
对于③,频率与试验次数相关,而概率与试验次数无关,所以③正确;
对于④,对于不同批次的试验,频率不一定相同,但概率相同,因而频率是概率的近似值,概率是频率的稳定值,所以④正确.
由概率和频率的定义中可知①③④正确.
故答案为: ①③④
7、某水产试验厂进行某种鱼卵的人工孵化,6个试验小组记录了不同的鱼卵数所孵化出的鱼苗数,如下表所示:
鱼卵数 200 600 900 1200 1800 2400
孵化出的鱼苗数 188 548 817 1067 1614 2163
孵化成功的频率 0.940 0.913 0.908 ① 0.897 ②
(1)表中①②对应的频率分别为多少(结果保留三位小数)?
(2)估计这种鱼卵孵化成功的概率.
(3)要孵化5000尾鱼苗,大概需要鱼卵多少个(精确到百位)?
【答案】(1)(2)0.9(3)
【分析】
(1)计算的值,即可得答案;
(2)从表中数据可看出,虽然频率都不一样,但随着试验的鱼卵数不断增多,孵化成功的频率稳定在0.9附近,即可得答案;
(3)利用频率等于频数除以总数计算,即可得答案.
【详解】
(1),所以①②对应的频率分别为.
(2)从表中数据可看出,虽然频率都不一样,但随着试验的鱼卵数不断增多,孵化成功的频率稳定在0.9附近,由此可估计该种鱼卵孵化成功的概率为0.9.
(3)大概需要鱼卵(个).
8、某市统计近几年婴儿出生数及其中男婴数(单位:人)如下:
出生婴儿数 21840 23070 20094 19982
出生男婴数 11453 12031 10297 10242
(1)试计算这几年男婴出生的频率(精确到0.001);
(2)估计该男婴出生的概率(精确到0.1).
【答案】(1),,,(2)0.5
【分析】
(1)根据所给数表,可依次计算出这几年男婴出生的频率;
(2)由频率估计概率,即可得解.
【详解】
(1)由表格可知,男婴出生的概率分别为
,
,
,
.
(2)由(1)中频率可估计该市男婴出生的概率为0.5.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
