6.4.1-6.4.2 平面几何中的向量方法、向量在物理中的应用-【新教材】2020-2021学年人教A版(2019)高一必修第二册课件(18张PPT)
文档属性
| 名称 | 6.4.1-6.4.2 平面几何中的向量方法、向量在物理中的应用-【新教材】2020-2021学年人教A版(2019)高一必修第二册课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 21:05:07 | ||
图片预览






文档简介
第六章 平面向量及其应用
6.4.1-6.4.2 平面几何中的向量方法、向量在物理中的应用
使用教材:人教A版2019必修第二册
授课教师:李祥老师
温故知新
回顾上节课所学五关斩六将的内容:
一关一将: a·b=x1x2+y1y2
二关二将:
二关三将:
a⊥b
x1x2+y1y2=0
a∥b
x1y2-x2y1=0
三关四将:
四关五将:
五关六将:
几何运算比较笨拙,没有向量运算的灵活性,
而向量的线性运算和数量积运算具有鲜明的几
何背景,
思考,我们是不是能够把向量引入几何解决几
何问题了?
新课引入
例1 如图6.4-1,DE是 的中位线,用向量的方法证明:
所以
又
所以
所以
例题解析
证明:如图,因为DE 是 的中位线,所以
课堂探究
(1)建立平面几何与向量的联系,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系;
(3)把运算结果“翻译”成几何关系。
用向量方法解决平面几何问题的“三步曲”:
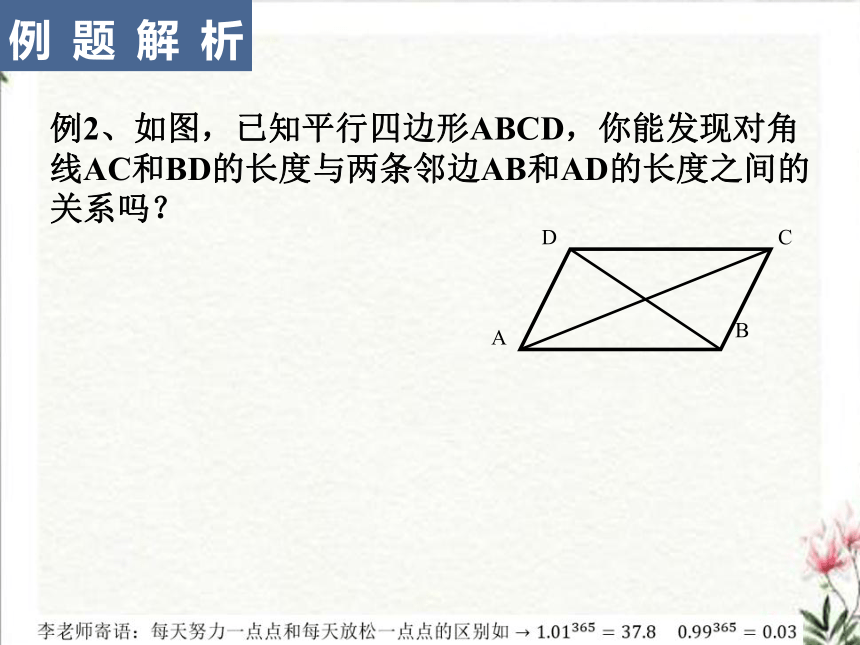
例2、如图,已知平行四边形ABCD,你能发现对角
线AC和BD的长度与两条邻边AB和AD的长度之间的
关系吗?
A
B
D
C
例题解析
课堂探究
A
B
D
C
第一步:建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
第二步:通过向量运算,研究几何元
素之间的关系,如距离、夹角等问题;
第三步:把运算结果“翻译”成几何关系。
上面两式相加,得
设 ,则
课堂探究
A
B
D
C
方法二:以A点为坐标原点,AB为x轴,建立如图所示的直角坐标系.
x
y
欣赏新题型
欣赏新题型
例4用两条成120°角的等长绳子悬挂一个灯
具,已知灯具重量为10 N,则每根绳子的拉力
大小为 。
例题解析
12
练习巩固
×
×
×
√
练习巩固
√
√
√
练习巩固
练习巩固
练习巩固
你学到了什么?
你认为易错点是哪些?
课堂小结
作业1:书本P39 P41
作业2:小试卷
作业3:预习余弦定理
作业布置
6.4.1-6.4.2 平面几何中的向量方法、向量在物理中的应用
使用教材:人教A版2019必修第二册
授课教师:李祥老师
温故知新
回顾上节课所学五关斩六将的内容:
一关一将: a·b=x1x2+y1y2
二关二将:
二关三将:
a⊥b
x1x2+y1y2=0
a∥b
x1y2-x2y1=0
三关四将:
四关五将:
五关六将:
几何运算比较笨拙,没有向量运算的灵活性,
而向量的线性运算和数量积运算具有鲜明的几
何背景,
思考,我们是不是能够把向量引入几何解决几
何问题了?
新课引入
例1 如图6.4-1,DE是 的中位线,用向量的方法证明:
所以
又
所以
所以
例题解析
证明:如图,因为DE 是 的中位线,所以
课堂探究
(1)建立平面几何与向量的联系,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系;
(3)把运算结果“翻译”成几何关系。
用向量方法解决平面几何问题的“三步曲”:
例2、如图,已知平行四边形ABCD,你能发现对角
线AC和BD的长度与两条邻边AB和AD的长度之间的
关系吗?
A
B
D
C
例题解析
课堂探究
A
B
D
C
第一步:建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
第二步:通过向量运算,研究几何元
素之间的关系,如距离、夹角等问题;
第三步:把运算结果“翻译”成几何关系。
上面两式相加,得
设 ,则
课堂探究
A
B
D
C
方法二:以A点为坐标原点,AB为x轴,建立如图所示的直角坐标系.
x
y
欣赏新题型
欣赏新题型
例4用两条成120°角的等长绳子悬挂一个灯
具,已知灯具重量为10 N,则每根绳子的拉力
大小为 。
例题解析
12
练习巩固
×
×
×
√
练习巩固
√
√
√
练习巩固
练习巩固
练习巩固
你学到了什么?
你认为易错点是哪些?
课堂小结
作业1:书本P39 P41
作业2:小试卷
作业3:预习余弦定理
作业布置
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
