6.1平面向量的概念-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(17张PPT)
文档属性
| 名称 | 6.1平面向量的概念-【新教材】2020-2021学年人教A版(2019)高中数学必修第二册课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 20:57:58 | ||
图片预览






文档简介
第六章 平面向量及其应用
6.1平面向量的概念
使用教材:人教A版必修第二册
授课教师:
2、请同学们回忆在物理中学习过哪些既有大小又有方向的量?
G
F
1.小船快速向东南方向航行
2.桌面承受物体的重力
3.浮力让物体浮起来
1、请同学们回忆物理里面,标量是什么 ?矢量是什么?
新课引入
力、位移、速度各有特性,但也有共同属性,请问共同属性是什么?
在现实生活中,一些量如长度、面积、质量、年龄等和刚才几个量一样吗?
只有大小,数学中称之为数量.
既有大小,又有方向.大家猜猜数学中称之为什么?
新课引入
下列不是向量的是( )
① 质量; ② 速度; ③位移; ④温度;
⑤加速度; ⑥路程; ⑦ 密度;⑧功.
① ④ ⑥⑦ ⑧
【即时训练】
向量的定义
既有大小又有方向的量叫做向量.
探求新知
AB
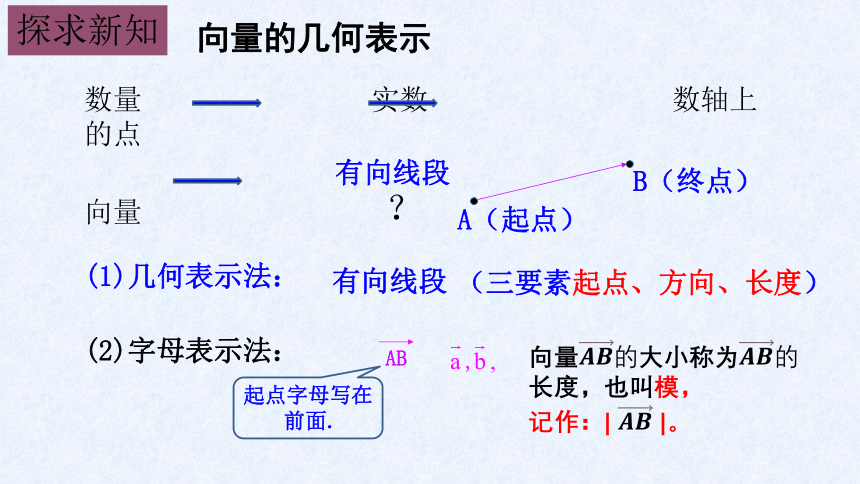
向量的几何表示
有向线段
(三要素起点、方向、长度)
(1)几何表示法:
(2)字母表示法:
B(终点)
A(起点)
数量 实数 数轴上的点
向量 ?
有向线段
起点字母写在前面.
向量????????的大小称为????????的长度,也叫模,
记作:| ???????? |。
?
探求新知
向量的有关概念
有向线段的长度表示向量的大小.
箭头所指的方向表示向量的方向.
向量AB的大小称为向量AB的长度(或称模),记作| ???????? |
?
两个特殊向量:
零向量——长度为0的向量叫做零向量,记作 0.
单位向量——长度等于1个单位长度的向量,叫做单位向量.
◆
◆
◆
◆
◆
探求新知
思考:向量和数量的区别和联系有哪些?
探求新知
数量只有大小,没有方向.可以进行代数运算、比较大小;向量有方向,大小,不能比较大小.
D
【即时训练1】
问:在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?
P
圆的半径是多少?
【即时训练2】
通过预习我们知道:什么是平行向量?
那么请问重合的向量是平行向量吗?
向量的平行与直线的平行有什么区别?
什么是相等向量?
方向相同或相反的非零向量叫做平行向量.我们规定:零向量与任意向量平行.
向量 ???? 与 ???? 平行,记作: ???? // ????
?
长度相等且方向相同的向量叫做相等向量。记作: ???? = ????
?
探求新知
什么是共线向量?为什么?
平行向量就是共线向量。
探求新知
例题1:如图6.1-8,设O是正六边形ABCDEF的中心.
(1)写出图中分别与 的共线向量;
(2)分别写出图中与 ,相等的向量.
例题展示
1.思维辨析(对的打“√”,错的打“×”)
(1)两个有共同起点,且长度相等的向量,它们的终点相同.( )
(2)向量就是有向线段.( )
(3)零向量是最小的向量.( )
(4)单位向量都是同方向.( )
(5)长度为0的向量都是零向量.( )
(6)单位向量的长度都相等.( )
×
×
×
×
√
√
练习巩固
B
练习巩固
3.下列说法中错误的是( )
A.零向量是没有方向的
B.零向量的长度为0
C.零向量与任一向量平行
D.零向量的方向是任意的
A
练习巩固
你学到了什么?
课堂小结
作业布置
作业1:书本P4—P5
作业2:新优化P1—P4
6.1平面向量的概念
使用教材:人教A版必修第二册
授课教师:
2、请同学们回忆在物理中学习过哪些既有大小又有方向的量?
G
F
1.小船快速向东南方向航行
2.桌面承受物体的重力
3.浮力让物体浮起来
1、请同学们回忆物理里面,标量是什么 ?矢量是什么?
新课引入
力、位移、速度各有特性,但也有共同属性,请问共同属性是什么?
在现实生活中,一些量如长度、面积、质量、年龄等和刚才几个量一样吗?
只有大小,数学中称之为数量.
既有大小,又有方向.大家猜猜数学中称之为什么?
新课引入
下列不是向量的是( )
① 质量; ② 速度; ③位移; ④温度;
⑤加速度; ⑥路程; ⑦ 密度;⑧功.
① ④ ⑥⑦ ⑧
【即时训练】
向量的定义
既有大小又有方向的量叫做向量.
探求新知
AB
向量的几何表示
有向线段
(三要素起点、方向、长度)
(1)几何表示法:
(2)字母表示法:
B(终点)
A(起点)
数量 实数 数轴上的点
向量 ?
有向线段
起点字母写在前面.
向量????????的大小称为????????的长度,也叫模,
记作:| ???????? |。
?
探求新知
向量的有关概念
有向线段的长度表示向量的大小.
箭头所指的方向表示向量的方向.
向量AB的大小称为向量AB的长度(或称模),记作| ???????? |
?
两个特殊向量:
零向量——长度为0的向量叫做零向量,记作 0.
单位向量——长度等于1个单位长度的向量,叫做单位向量.
◆
◆
◆
◆
◆
探求新知
思考:向量和数量的区别和联系有哪些?
探求新知
数量只有大小,没有方向.可以进行代数运算、比较大小;向量有方向,大小,不能比较大小.
D
【即时训练1】
问:在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?
P
圆的半径是多少?
【即时训练2】
通过预习我们知道:什么是平行向量?
那么请问重合的向量是平行向量吗?
向量的平行与直线的平行有什么区别?
什么是相等向量?
方向相同或相反的非零向量叫做平行向量.我们规定:零向量与任意向量平行.
向量 ???? 与 ???? 平行,记作: ???? // ????
?
长度相等且方向相同的向量叫做相等向量。记作: ???? = ????
?
探求新知
什么是共线向量?为什么?
平行向量就是共线向量。
探求新知
例题1:如图6.1-8,设O是正六边形ABCDEF的中心.
(1)写出图中分别与 的共线向量;
(2)分别写出图中与 ,相等的向量.
例题展示
1.思维辨析(对的打“√”,错的打“×”)
(1)两个有共同起点,且长度相等的向量,它们的终点相同.( )
(2)向量就是有向线段.( )
(3)零向量是最小的向量.( )
(4)单位向量都是同方向.( )
(5)长度为0的向量都是零向量.( )
(6)单位向量的长度都相等.( )
×
×
×
×
√
√
练习巩固
B
练习巩固
3.下列说法中错误的是( )
A.零向量是没有方向的
B.零向量的长度为0
C.零向量与任一向量平行
D.零向量的方向是任意的
A
练习巩固
你学到了什么?
课堂小结
作业布置
作业1:书本P4—P5
作业2:新优化P1—P4
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
