【新人教B版】(新教材)2020-2021学年高中11.4.2平面与平面垂直课件必修第四册(数学)(55张PPT)
文档属性
| 名称 | 【新人教B版】(新教材)2020-2021学年高中11.4.2平面与平面垂直课件必修第四册(数学)(55张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 828.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-28 00:00:00 | ||
图片预览









文档简介
11.4.2 平面与平面垂直
基础预习初探
1.教室拐角处相邻的两个墙面是什么位置关系?教室的墙面与地面是什么位置关系?怎样用符号表示这种位置关系?
2.拿一张木板紧贴旗杆,则木板所在的平面与地面具有怎样的位置关系?由此你能找到判定两个平面垂直的方法吗?
继续探究:
(1)建筑工人常在一根细线上拴一个重物,做成“铅锤”,用这种方法来检查墙与地面是否垂直.当挂铅锤的线从上面某一点垂下时,如果墙壁贴近铅锤线,则说明墙和地面什么关系?此时铅锤线与地面什么关系?
提示:都是垂直关系.
(2)黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
提示:容易发现墙壁与墙壁所在平面的交线与地面垂直,因此只要在黑板上画出一条与这条交线平行的直线,则所画直线必与地面垂直.
【概念生成】
1.二面角
(1)定义:从_________出发的两个半平面所组成的图形称为二面角.
(2)表示法:二面角α-l-β或二面角α-AB-β或P-AB-Q.
(3)相关概念:①定义中的直线叫做二面角的___;
②定义中的两个半平面叫做二面角的___.
一条直线
棱
面
(4)画法:
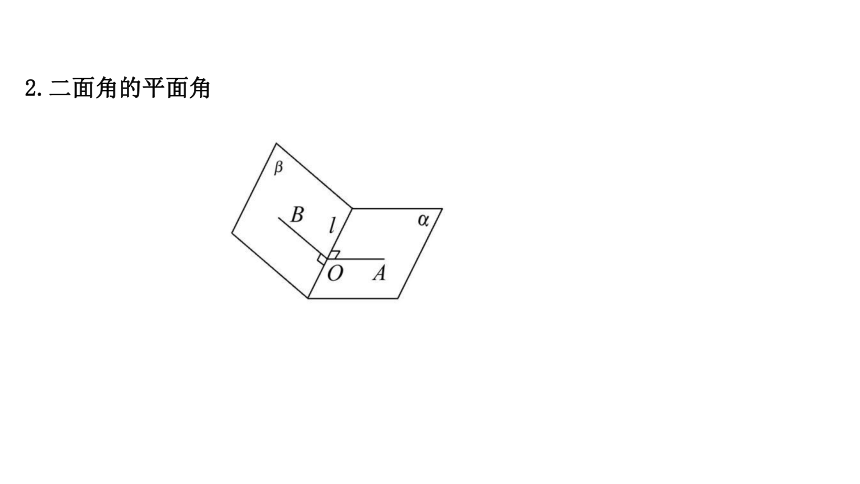
2.二面角的平面角
(1)满足条件:如图:
α∩β=l,O∈l,OA?α,_____,OB?β,_____.
(2)结论:∠AOB叫做二面角的平面角.
(3)范围:__________________.
(4)直二面角:若二面角α-l-β的平面角∠AOB=90°,则该二面角叫做
_________.
OA⊥l
OB⊥l
0°≤∠AOB≤180°
直二面角
3.平面与平面垂直
(1)定义:如果两个平面α与β所成角的大小为90°,则称这两个平面互相垂直,记作α⊥β.
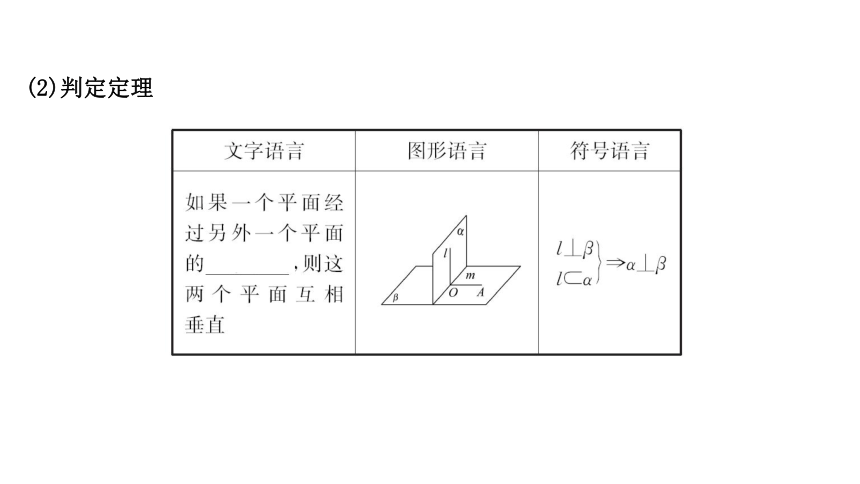
(2)判定定理
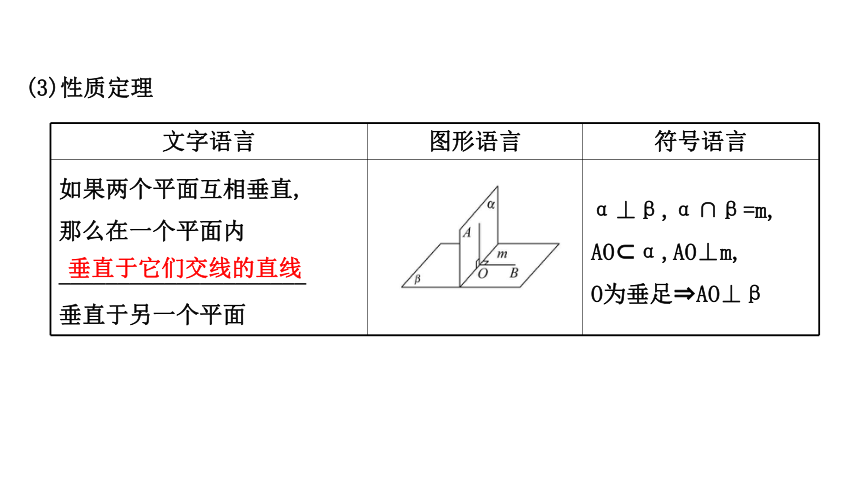
(3)性质定理
文字语言
图形语言
符号语言
如果两个平面互相垂直,
那么在一个平面内
_____________________
垂直于另一个平面
α⊥β,α∩β=m,
AO?α,AO⊥m,
O为垂足?AO⊥β
垂直于它们交线的直线
核心互动探究
探究点一 二面角的求解
【典例1】已知正四棱锥S-ABCD(底面为正方形,各侧面为全等的等腰三角形)
的体积为12,底面对角线的长为2 ,求侧面与底面所成的二面角.
【思维导引】作出S在底面上的投影O,作OE⊥CD于E,连接SE,证明∠SEO为
所求二面角的平面角.
【解析】设正四棱锥S-ABCD的高为h,底面边长为a,
则2a2=(2 )2,
所以a2=12.
又 a2h=12,所以h= =3.
设O为S在底面上的投影,作OE⊥CD于E,连接SE,
可知SE⊥CD,∠SEO为所求二面角的平面角.
tan∠SEO= 所以∠SEO=60°.
所以侧面与底面所成二面角的大小为60°.
【延伸探究】在本例条件下,求二面角D-SC-A的正弦值.
【解析】如图,过点O作OF⊥SC,垂足为F,连接FD,OD,AC.
由例题解析知,SO⊥平面ABCD,且O是底面正方形的中心,所以DO⊥SO,DO⊥AC,
又AC∩SO=O.所以DO⊥平面SAC,
又SC?平面SAC,所以SC⊥DO,
又SC⊥OF,DO∩OF=O.所以SC⊥平面DOF,
又DF?平面DOF,所以DF⊥SC.
所以∠OFD为二面角D-SC-A的平面角.
由例题知,OD= ,
所以DF=
所以sin∠OFD=
即二面角D-SC-A的正弦值为
【类题通法】
求二面角的步骤
(1)作出二面角的平面角.
(2)证明该角两边都与棱垂直,指出该角就是二面角的平面角.
(3)计算该角的大小,简记为作、证、求,简称为“一作二证三求”.
【定向训练】
已知D,E分别是正三棱柱ABC-A1B1C1的侧棱AA1和BB1上的点,且A1D=2B1E=B1C1.求过D,E,C1的平面与棱柱的下底面A1B1C1所成的二面角的大小.
【解析】如图所示,
在平面A1B1B内延长DE和A1B1交于点F,
则F是平面DEC1与平面A1B1C1的公共点.于是C1F为这两个平面的交线.
因而,所求二面角即为二面角D-C1F-A1.
因为A1D∥B1E,且A1D=2B1E,
所以E,B1分别为DF和A1F的中点.
因为A1B1=B1C1=A1C1=B1F,
所以FC1⊥A1C1.
又因为CC1⊥平面A1B1C1,FC1?平面A1B1C1,
所以CC1⊥FC1.
又因为A1C1,CC1为平面AA1C1C内的两条相交直线,
所以FC1⊥平面AA1C1C.
因为DC1?平面AA1C1C,
所以FC1⊥DC1.
所以∠DC1A1是二面角D-C1F-A1的平面角.
由已知A1D=A1C1,
则∠DC1A1=45°.
故所求二面角的大小为45°.
【补偿训练】
已知Rt△ABC,斜边BC?α,点A?α,AO⊥α,O为垂足,∠ABO=30°,
∠ACO=45°,则二面角A-BC-O的大小为________.?
【解析】如图,在平面ABC内,
作AD⊥BC,且垂足为D,连接OD,
则∠ADO即为二面角A-BC-O的平面角,
设OA=1,则AB=2,OB= ,OC=1,AC= ,
所以BC=
由AB·AC=BC·AD得AD=
所以sin∠ADO=
又因为0°<∠ADO<90°,所以∠ADO=60°,
所以二面角A-BC-O的大小为60°.
答案:60°
探究点二 平面与平面垂直的判定
【典例2】如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(1)DE=DA.
(2)平面BDM⊥平面ECA.
(3)平面DEA⊥平面ECA.
【思维导引】(1)取EC的中点F,要证DE=DA,只需证明Rt△EFD≌Rt△DBA;(2)注意M为EA的中点,可取CA的中点N,先证明N点在平面BDM内,再证明平面BDM过平面ECA的一条垂线即可;
(3)仍需证平面DEA经过平面ECA的一条垂线.
【证明】(1)取EC的中点F,连接DF.
因为EC⊥BC,易知DF∥BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中,
因为EF= EC=BD,FD=BC=AB,
所以Rt△EFD≌Rt△DBA.所以DE=DA.
(2)取CA的中点N,连接MN,BN,
则MN???? EC,所以MN∥BD,
所以N点在平面BDMN内.
因为EC⊥平面ABC,所以EC⊥BN.
又CA⊥BN,CA∩EC=C,所以BN⊥平面ECA.
因为BN在平面MNBD内,
所以平面MNBD⊥平面ECA.
即平面BDM⊥平面ECA.
(3)因为BD???? EC,MN???? EC.
所以MNBD为平行四边形.所以DM∥BN.
由(2)知BN⊥平面ECA,所以DM⊥平面ECA.
又DM?平面DEA,所以平面DEA⊥平面ECA.
【类题通法】
应用判定定理证明平面与平面垂直的基本步骤
【定向训练】
(2020·全国Ⅰ卷)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P为DO上一点,∠APC=90°.
证明:平面PAB⊥平面PAC.
【证明】由题设可知,PA=PB=PC.
由于△ABC是正三角形,故可得△PAC≌△PAB.
△PAC≌△PBC.
又∠APC =90°,故∠APB=90°,∠BPC=90°.
从而PB⊥PA,PB⊥PC,故PB⊥平面PAC,因为PB在平面PAB内,所以平面PAB⊥平面PAC.
【补偿训练】
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上,
求证:平面AEC⊥平面PDB.
【证明】设AC∩BD=O,连接OE,
因为AC⊥BD,AC⊥PD,PD,BD为平面PDB内两条相交直线,所以AC⊥平面PDB.
又因为AC?平面AEC,
所以平面AEC⊥平面PDB.
探究点三 面面垂直性质定理的应用
【典例3】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD的中点,求证:BG⊥平面PAD.
(2)求证:AD⊥PB.
【思维导引】(1)由四边形ABCD为菱形,∠DAB=60°得到△ABD为正三角形,G为AD的中点,推出BG⊥AD,结合平面PAD⊥底面ABCD得到BG⊥平面PAD.
(2)连接PG,要证AD⊥PB,只需证AD⊥平面PBG即可.
【证明】(1)如图,在菱形ABCD中,连接BD,
由已知∠DAB=60°,所以△ABD为正三角形,
因为G是AD的中点,所以BG⊥AD.
因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
(2)连接PG.
因为△PAD是正三角形,G是AD的中点,
所以PG⊥AD,由(1)知BG⊥AD.
又因为PG∩BG=G.所以AD⊥平面PBG.
而PB?平面PBG,所以AD⊥PB.
【类题通法】
垂直关系的相互转化
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化.每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
提醒:应用面面垂直的性质定理,注意三点:①两个平面垂直是前提条件;②直线必须在其中一个平面内;③直线必须垂直于它们的交线.
【定向训练】
(2020·浙江高考)如图,三棱台DEF-ABC中,面ADFC⊥面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求DF与面DBC所成角的正弦值.
【解析】(Ⅰ)过点D作DO⊥AC,交AC于点O,连接OB.
由∠ACD=45°,DO⊥AC得CD= CO,
由平面ACFD⊥平面ABC得DO⊥平面ABC,所以DO⊥BC.
由∠ACB=45°,BC= CD= CO,可解得BO⊥BC,
又BO∩DO=O,BO,DO?平面BDO,
所以BC⊥平面BDO,因为DB?平面BDO,所以BC⊥DB.
由三棱台ABC-DEF得BC∥EF,所以EF⊥DB.
(Ⅱ)方法一:过点O作OH⊥BD,交BD于点H,连接CH.
由三棱台ABC-DEF得DF∥CO,
所以DF与平面DBC所成角等于CO与平面DBC所成角.
由BC⊥平面BDO得OH⊥BC,又BD∩BC=B,BD,BC?平面BDC,所以OH⊥平面BCD,
所以∠OCH为直线CO与平面DBC所成角.设CD=2 .
则DO=OC=2,BO=BC= ,所以BD= ,OH=
所以sin ∠OCH=
因此,直线DF与平面DBC所成角的正弦值为 .
方法二:由三棱台ABC-DEF得DF∥CO,所以DF与平面DBC所成角等于CO与平面DBC所成角,记为θ.
如图,以O为原点,分别以射线OC,OD为y,z轴的正半轴,建立空间直角坐标系.
设CD=2 .由题意知各点坐标如下:
O(0,0,0),B(1,1,0),C(0,2,0),D(0,0,2).
因此 =(0,2,0), =(-1,1,0), =(0,-2,2).
设平面BCD的法向量n=(x,y,z).
由 可取n=(1,1,1),
所以sin θ=|cos< ,n>|=
因此,DF与平面DBC所成角的正弦值为 .
【补偿训练】
如图所示,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(1)求证:AE∥平面BCD.
(2)求证:平面BDE⊥平面CDE.
【证明】(1)取BC的中点M,连接DM,
因为BD=CD,且BD⊥CD,BC=2.
所以DM=1,DM⊥BC.
又因为平面BCD⊥平面ABC,平面ABC∩平面BCD=BC,
所以DM⊥平面ABC,又AE⊥平面ABC,所以AE∥DM.
又因为AE?平面BCD,DM?平面BCD,
所以AE∥平面BCD.
(2)连接AM,由(1)知AE∥DM,
又AE=1,DM=1,所以AE=DM,
所以四边形DMAE是平行四边形,
所以DE∥AM.
又△ABC是正三角形,M为BC的中点,
所以AM⊥BC,因为平面BCD⊥平面ABC,
所以AM⊥平面BCD,所以DE⊥平面BCD.
又CD?平面BCD,所以DE⊥CD.
因为BD⊥CD,BD∩DE=D,
所以CD⊥平面BDE.
因为CD?平面CDE,所以平面BDE⊥平面CDE.
【课堂小结】
课堂素养达标
1.长方体ABCD-A1B1C1D1的六个面中,与面ABCD垂直的面有 ( )
A.1个 B.3个 C.4个 D.5个
【解析】选C.与面ABCD垂直的面有面ABB1A1,面BCC1B1,面CDD1C1,面DAA1D1,共4个.
2.设l是直线,α,β是两个不同的平面 ( )
A.若l∥α,l∥β,则α∥β
B.l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β
D.α⊥β,l∥α,则l⊥β
【解析】选B.对于选项A,两平面可能平行也可能相交;对于选项C,直线l可能在β内也可能平行于β;对于选项D,直线l可能在β内或平行于β或与β相交.
3.对于直线m,n和平面α,β,能得出α⊥β的一个条件是 ( )
A.m⊥n,m∥α,n∥β
B.m⊥n,α∩β=m,n?α
C.m∥n,n⊥β,m?α
D.m∥n,m⊥α,n⊥β
【解析】选C.因为m∥n,n⊥β,则m⊥β,
又m?α,故α⊥β,所以C正确.
4.在空间四面体S-ABC中,SC⊥AB,AC⊥SC,且△ABC是锐角三角形,
那么必有 ( )
A.平面SAC⊥平面SCB
B.平面SAB⊥平面ABC
C.平面SAC⊥平面SAB
D.平面SCB⊥平面ABC
【解析】选D.如图,因为SC⊥AB,SC⊥AC,AB∩AC=A,
所以SC⊥平面ABC.所以平面SCB⊥平面ABC.
基础预习初探
1.教室拐角处相邻的两个墙面是什么位置关系?教室的墙面与地面是什么位置关系?怎样用符号表示这种位置关系?
2.拿一张木板紧贴旗杆,则木板所在的平面与地面具有怎样的位置关系?由此你能找到判定两个平面垂直的方法吗?
继续探究:
(1)建筑工人常在一根细线上拴一个重物,做成“铅锤”,用这种方法来检查墙与地面是否垂直.当挂铅锤的线从上面某一点垂下时,如果墙壁贴近铅锤线,则说明墙和地面什么关系?此时铅锤线与地面什么关系?
提示:都是垂直关系.
(2)黑板所在平面与地面所在平面垂直,你能否在黑板上画一条直线与地面垂直?
提示:容易发现墙壁与墙壁所在平面的交线与地面垂直,因此只要在黑板上画出一条与这条交线平行的直线,则所画直线必与地面垂直.
【概念生成】
1.二面角
(1)定义:从_________出发的两个半平面所组成的图形称为二面角.
(2)表示法:二面角α-l-β或二面角α-AB-β或P-AB-Q.
(3)相关概念:①定义中的直线叫做二面角的___;
②定义中的两个半平面叫做二面角的___.
一条直线
棱
面
(4)画法:
2.二面角的平面角
(1)满足条件:如图:
α∩β=l,O∈l,OA?α,_____,OB?β,_____.
(2)结论:∠AOB叫做二面角的平面角.
(3)范围:__________________.
(4)直二面角:若二面角α-l-β的平面角∠AOB=90°,则该二面角叫做
_________.
OA⊥l
OB⊥l
0°≤∠AOB≤180°
直二面角
3.平面与平面垂直
(1)定义:如果两个平面α与β所成角的大小为90°,则称这两个平面互相垂直,记作α⊥β.
(2)判定定理
(3)性质定理
文字语言
图形语言
符号语言
如果两个平面互相垂直,
那么在一个平面内
_____________________
垂直于另一个平面
α⊥β,α∩β=m,
AO?α,AO⊥m,
O为垂足?AO⊥β
垂直于它们交线的直线
核心互动探究
探究点一 二面角的求解
【典例1】已知正四棱锥S-ABCD(底面为正方形,各侧面为全等的等腰三角形)
的体积为12,底面对角线的长为2 ,求侧面与底面所成的二面角.
【思维导引】作出S在底面上的投影O,作OE⊥CD于E,连接SE,证明∠SEO为
所求二面角的平面角.
【解析】设正四棱锥S-ABCD的高为h,底面边长为a,
则2a2=(2 )2,
所以a2=12.
又 a2h=12,所以h= =3.
设O为S在底面上的投影,作OE⊥CD于E,连接SE,
可知SE⊥CD,∠SEO为所求二面角的平面角.
tan∠SEO= 所以∠SEO=60°.
所以侧面与底面所成二面角的大小为60°.
【延伸探究】在本例条件下,求二面角D-SC-A的正弦值.
【解析】如图,过点O作OF⊥SC,垂足为F,连接FD,OD,AC.
由例题解析知,SO⊥平面ABCD,且O是底面正方形的中心,所以DO⊥SO,DO⊥AC,
又AC∩SO=O.所以DO⊥平面SAC,
又SC?平面SAC,所以SC⊥DO,
又SC⊥OF,DO∩OF=O.所以SC⊥平面DOF,
又DF?平面DOF,所以DF⊥SC.
所以∠OFD为二面角D-SC-A的平面角.
由例题知,OD= ,
所以DF=
所以sin∠OFD=
即二面角D-SC-A的正弦值为
【类题通法】
求二面角的步骤
(1)作出二面角的平面角.
(2)证明该角两边都与棱垂直,指出该角就是二面角的平面角.
(3)计算该角的大小,简记为作、证、求,简称为“一作二证三求”.
【定向训练】
已知D,E分别是正三棱柱ABC-A1B1C1的侧棱AA1和BB1上的点,且A1D=2B1E=B1C1.求过D,E,C1的平面与棱柱的下底面A1B1C1所成的二面角的大小.
【解析】如图所示,
在平面A1B1B内延长DE和A1B1交于点F,
则F是平面DEC1与平面A1B1C1的公共点.于是C1F为这两个平面的交线.
因而,所求二面角即为二面角D-C1F-A1.
因为A1D∥B1E,且A1D=2B1E,
所以E,B1分别为DF和A1F的中点.
因为A1B1=B1C1=A1C1=B1F,
所以FC1⊥A1C1.
又因为CC1⊥平面A1B1C1,FC1?平面A1B1C1,
所以CC1⊥FC1.
又因为A1C1,CC1为平面AA1C1C内的两条相交直线,
所以FC1⊥平面AA1C1C.
因为DC1?平面AA1C1C,
所以FC1⊥DC1.
所以∠DC1A1是二面角D-C1F-A1的平面角.
由已知A1D=A1C1,
则∠DC1A1=45°.
故所求二面角的大小为45°.
【补偿训练】
已知Rt△ABC,斜边BC?α,点A?α,AO⊥α,O为垂足,∠ABO=30°,
∠ACO=45°,则二面角A-BC-O的大小为________.?
【解析】如图,在平面ABC内,
作AD⊥BC,且垂足为D,连接OD,
则∠ADO即为二面角A-BC-O的平面角,
设OA=1,则AB=2,OB= ,OC=1,AC= ,
所以BC=
由AB·AC=BC·AD得AD=
所以sin∠ADO=
又因为0°<∠ADO<90°,所以∠ADO=60°,
所以二面角A-BC-O的大小为60°.
答案:60°
探究点二 平面与平面垂直的判定
【典例2】如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,求证:
(1)DE=DA.
(2)平面BDM⊥平面ECA.
(3)平面DEA⊥平面ECA.
【思维导引】(1)取EC的中点F,要证DE=DA,只需证明Rt△EFD≌Rt△DBA;(2)注意M为EA的中点,可取CA的中点N,先证明N点在平面BDM内,再证明平面BDM过平面ECA的一条垂线即可;
(3)仍需证平面DEA经过平面ECA的一条垂线.
【证明】(1)取EC的中点F,连接DF.
因为EC⊥BC,易知DF∥BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中,
因为EF= EC=BD,FD=BC=AB,
所以Rt△EFD≌Rt△DBA.所以DE=DA.
(2)取CA的中点N,连接MN,BN,
则MN???? EC,所以MN∥BD,
所以N点在平面BDMN内.
因为EC⊥平面ABC,所以EC⊥BN.
又CA⊥BN,CA∩EC=C,所以BN⊥平面ECA.
因为BN在平面MNBD内,
所以平面MNBD⊥平面ECA.
即平面BDM⊥平面ECA.
(3)因为BD???? EC,MN???? EC.
所以MNBD为平行四边形.所以DM∥BN.
由(2)知BN⊥平面ECA,所以DM⊥平面ECA.
又DM?平面DEA,所以平面DEA⊥平面ECA.
【类题通法】
应用判定定理证明平面与平面垂直的基本步骤
【定向训练】
(2020·全国Ⅰ卷)如图,D为圆锥的顶点,O是圆锥底面的圆心,△ABC是底面的内接正三角形,P为DO上一点,∠APC=90°.
证明:平面PAB⊥平面PAC.
【证明】由题设可知,PA=PB=PC.
由于△ABC是正三角形,故可得△PAC≌△PAB.
△PAC≌△PBC.
又∠APC =90°,故∠APB=90°,∠BPC=90°.
从而PB⊥PA,PB⊥PC,故PB⊥平面PAC,因为PB在平面PAB内,所以平面PAB⊥平面PAC.
【补偿训练】
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上,
求证:平面AEC⊥平面PDB.
【证明】设AC∩BD=O,连接OE,
因为AC⊥BD,AC⊥PD,PD,BD为平面PDB内两条相交直线,所以AC⊥平面PDB.
又因为AC?平面AEC,
所以平面AEC⊥平面PDB.
探究点三 面面垂直性质定理的应用
【典例3】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.
(1)若G为AD的中点,求证:BG⊥平面PAD.
(2)求证:AD⊥PB.
【思维导引】(1)由四边形ABCD为菱形,∠DAB=60°得到△ABD为正三角形,G为AD的中点,推出BG⊥AD,结合平面PAD⊥底面ABCD得到BG⊥平面PAD.
(2)连接PG,要证AD⊥PB,只需证AD⊥平面PBG即可.
【证明】(1)如图,在菱形ABCD中,连接BD,
由已知∠DAB=60°,所以△ABD为正三角形,
因为G是AD的中点,所以BG⊥AD.
因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
(2)连接PG.
因为△PAD是正三角形,G是AD的中点,
所以PG⊥AD,由(1)知BG⊥AD.
又因为PG∩BG=G.所以AD⊥平面PBG.
而PB?平面PBG,所以AD⊥PB.
【类题通法】
垂直关系的相互转化
在关于垂直问题的论证中要注意线线垂直、线面垂直、面面垂直的相互转化.每一种垂直的判定都是从某一垂直开始转向另一垂直,最终达到目的,其转化关系如下:
提醒:应用面面垂直的性质定理,注意三点:①两个平面垂直是前提条件;②直线必须在其中一个平面内;③直线必须垂直于它们的交线.
【定向训练】
(2020·浙江高考)如图,三棱台DEF-ABC中,面ADFC⊥面ABC,∠ACB=∠ACD=45°,DC=2BC.
(Ⅰ)证明:EF⊥DB;
(Ⅱ)求DF与面DBC所成角的正弦值.
【解析】(Ⅰ)过点D作DO⊥AC,交AC于点O,连接OB.
由∠ACD=45°,DO⊥AC得CD= CO,
由平面ACFD⊥平面ABC得DO⊥平面ABC,所以DO⊥BC.
由∠ACB=45°,BC= CD= CO,可解得BO⊥BC,
又BO∩DO=O,BO,DO?平面BDO,
所以BC⊥平面BDO,因为DB?平面BDO,所以BC⊥DB.
由三棱台ABC-DEF得BC∥EF,所以EF⊥DB.
(Ⅱ)方法一:过点O作OH⊥BD,交BD于点H,连接CH.
由三棱台ABC-DEF得DF∥CO,
所以DF与平面DBC所成角等于CO与平面DBC所成角.
由BC⊥平面BDO得OH⊥BC,又BD∩BC=B,BD,BC?平面BDC,所以OH⊥平面BCD,
所以∠OCH为直线CO与平面DBC所成角.设CD=2 .
则DO=OC=2,BO=BC= ,所以BD= ,OH=
所以sin ∠OCH=
因此,直线DF与平面DBC所成角的正弦值为 .
方法二:由三棱台ABC-DEF得DF∥CO,所以DF与平面DBC所成角等于CO与平面DBC所成角,记为θ.
如图,以O为原点,分别以射线OC,OD为y,z轴的正半轴,建立空间直角坐标系.
设CD=2 .由题意知各点坐标如下:
O(0,0,0),B(1,1,0),C(0,2,0),D(0,0,2).
因此 =(0,2,0), =(-1,1,0), =(0,-2,2).
设平面BCD的法向量n=(x,y,z).
由 可取n=(1,1,1),
所以sin θ=|cos< ,n>|=
因此,DF与平面DBC所成角的正弦值为 .
【补偿训练】
如图所示,△ABC是边长为2的正三角形.若AE=1,AE⊥平面ABC,平面BCD⊥平面ABC,BD=CD,且BD⊥CD.
(1)求证:AE∥平面BCD.
(2)求证:平面BDE⊥平面CDE.
【证明】(1)取BC的中点M,连接DM,
因为BD=CD,且BD⊥CD,BC=2.
所以DM=1,DM⊥BC.
又因为平面BCD⊥平面ABC,平面ABC∩平面BCD=BC,
所以DM⊥平面ABC,又AE⊥平面ABC,所以AE∥DM.
又因为AE?平面BCD,DM?平面BCD,
所以AE∥平面BCD.
(2)连接AM,由(1)知AE∥DM,
又AE=1,DM=1,所以AE=DM,
所以四边形DMAE是平行四边形,
所以DE∥AM.
又△ABC是正三角形,M为BC的中点,
所以AM⊥BC,因为平面BCD⊥平面ABC,
所以AM⊥平面BCD,所以DE⊥平面BCD.
又CD?平面BCD,所以DE⊥CD.
因为BD⊥CD,BD∩DE=D,
所以CD⊥平面BDE.
因为CD?平面CDE,所以平面BDE⊥平面CDE.
【课堂小结】
课堂素养达标
1.长方体ABCD-A1B1C1D1的六个面中,与面ABCD垂直的面有 ( )
A.1个 B.3个 C.4个 D.5个
【解析】选C.与面ABCD垂直的面有面ABB1A1,面BCC1B1,面CDD1C1,面DAA1D1,共4个.
2.设l是直线,α,β是两个不同的平面 ( )
A.若l∥α,l∥β,则α∥β
B.l∥α,l⊥β,则α⊥β
C.若α⊥β,l⊥α,则l⊥β
D.α⊥β,l∥α,则l⊥β
【解析】选B.对于选项A,两平面可能平行也可能相交;对于选项C,直线l可能在β内也可能平行于β;对于选项D,直线l可能在β内或平行于β或与β相交.
3.对于直线m,n和平面α,β,能得出α⊥β的一个条件是 ( )
A.m⊥n,m∥α,n∥β
B.m⊥n,α∩β=m,n?α
C.m∥n,n⊥β,m?α
D.m∥n,m⊥α,n⊥β
【解析】选C.因为m∥n,n⊥β,则m⊥β,
又m?α,故α⊥β,所以C正确.
4.在空间四面体S-ABC中,SC⊥AB,AC⊥SC,且△ABC是锐角三角形,
那么必有 ( )
A.平面SAC⊥平面SCB
B.平面SAB⊥平面ABC
C.平面SAC⊥平面SAB
D.平面SCB⊥平面ABC
【解析】选D.如图,因为SC⊥AB,SC⊥AC,AB∩AC=A,
所以SC⊥平面ABC.所以平面SCB⊥平面ABC.
