2020-2021学年八年级数学人教版下册 18.1.1平行四边形的性质教案(表格式)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册 18.1.1平行四边形的性质教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 71.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览


文档简介
课题:18.1.1平行四边形的性质
课时:2-3课时
备课时间:
一、教学内容分析
四边形问题转化为三角形来解决的转化思想是本课的难点,教学过程中教师在通过逻辑分析的方法引导学生来突破难点,但是通过课堂实际观察笔者感觉到学生现阶段的思维发展状况与常用思维方法还是稍有差异。
二、教学目标
知识与技能
理解并掌握平行四边形的概念和平行四边形的性质;
过程与方法;
会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证;
情感态度、价值观
培养学生发现问题、解决问题的能力及逻辑推理能力。
三、学情分析
学生在小学已经学行四边形的基础知识,经历了针对图形的探究过程,知晓了平行四边形的边、角关系的结论,那么在此基础上的再次“观察、猜想、实验验证”就失去了其真正的意义,也很难激发学生的学习热情。
四、教学策略选择与设计
观察、猜想、实验验证。
五、教学重点及难点
重点:平行四边形的定义,平行四边形的性质,以及性质的应用.
2.难点:运用平行四边形的性质进行有关的论证和计算.
六、教学流程
课堂引入:
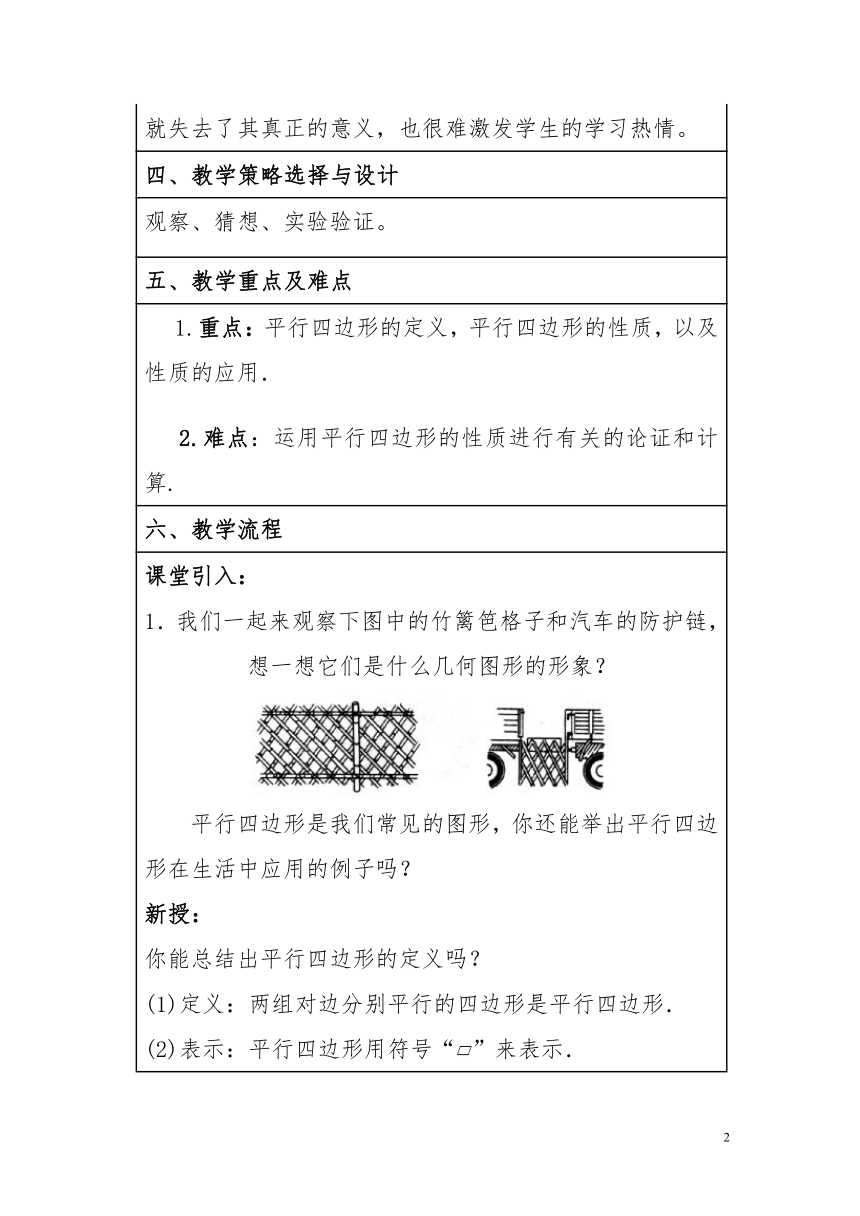
1.我们一起来观察下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
新授:
你能总结出平行四边形的定义吗?
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)表示:平行四边形用符号“”来表示.
如图,在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD记作“
ABCD”,读作“平行四边形ABCD”.
①∵AB//DC
,AD//BC
,
∴四边形ABCD是平行四边形(判定);
②∵四边形ABCD是平行四边形∴AB//DC,
AD//BC(性质).
注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.(教学时要结合图形,让学生认识清楚)
【探究】
平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?我们一起来探究一下.
让学生根据平行四边形的定义画一个一个平行四边形,观察这个四边形,它除具有四边形的性质和两组对边分别平行外以,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致?
(1)由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为补角.
(相邻的角指四边形中有一条公共边的两个角.注意和第一章的邻角相区别.教学时结合图形使学生分辨清楚.)
(2)猜想
平行四边形的对边相等、对角相等.
下面证明这个结论的正确性.
已知:如图
ABCD,
求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD.
分析:作
ABCD的对角线AC,它将平行四边形分成△ABC和△CDA,证明这两个三角形全等即可得到结论.
(作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.)
证明:连接AC,
∵
AB∥CD,AD∥BC,
∴
∠1=∠3,∠2=∠4.
又
AC=CA,
∴
△ABC≌△CDA
(ASA).
∴
AB=CD,CB=AD,∠B=∠D.
又
∠1+∠4=∠2+∠3,
∴
∠BAD=∠BCD.
由此得到:
平行四边形性质1 平行四边形的对边相等.
平行四边形性质2
平行四边形的对角相等.
例习题分析
例1(教材P42例1)
例2(补充)如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.
分析:要证AF=CE,需证△ADF≌△CBE,由于四边形ABCD是平行四边形,因此有∠D=∠B
,AD=BC,AB=CD,又AE=CF,根据等式性质,可得BE=DF.由“边角边”可得出所需要的结论.证明略.
完成课本P42-43的内容学习
两条平行线之间的距离:
两条平行线中,一条直线上任意一点到另一条直线的距离。
【探究】
完成课本P43“探究”
从而可以得到:
平行四边形性质:平行四边形的对角线互相平分。
引导学生证明以上性质。
例(教材P94的例2)已知四边形ABCD是平行四边形,AB=10cm,AD=8cm,AC⊥BC,求BC、CD、AC、OA的长以及ABCD的面积.
分析:由平行四边形的对边相等,可得BC、CD的长,在Rt△ABC中,由勾股定理可得AC的长.再由平行四边形的对角线互相平分可求得OA的长,根据平行四边形的面积计算公式:平行四边形的面积=底×高(高为此底上的高),可求得ABCD的面积.(平行四边形的面积小学学过,再次强调“底”是对应着高说的,平行四边形中,任一边都可以作为“底”,“底”确定后,高也就随之确定了.)3.平行四边形的面积计算.
解题过程略
随堂练习
1.填空:
(1)在
ABCD中,∠A=
,则∠B=
度,∠C=
度,∠D=
度.
(2)如果
ABCD中,∠A—∠B=240,则∠A=
度,∠B=
度,∠C=
度,∠D=
度.
(3)如果
ABCD的周长为28cm,且AB:BC=2∶5,那么AB=
cm,BC=
cm,CD=
cm,CD=
cm.
2.如图4.3-9,在
ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.
课堂小结
本节课我们学习了哪些内容?
课后练习
1.课本练习及习题;
2.在
ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有(
).
(A)4个
(B)5个
(C)8个
(D)9个
七、板书设计
1.标题
2.平行四边形的性质及推到;
3.性质的证明及例题;
八、教学反思
授课时间:
教研组检查情况:
组长签字:
年
月
日
教务处检查情况:
主任(教务员)签字:
年
月
日
1
课时:2-3课时
备课时间:
一、教学内容分析
四边形问题转化为三角形来解决的转化思想是本课的难点,教学过程中教师在通过逻辑分析的方法引导学生来突破难点,但是通过课堂实际观察笔者感觉到学生现阶段的思维发展状况与常用思维方法还是稍有差异。
二、教学目标
知识与技能
理解并掌握平行四边形的概念和平行四边形的性质;
过程与方法;
会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证;
情感态度、价值观
培养学生发现问题、解决问题的能力及逻辑推理能力。
三、学情分析
学生在小学已经学行四边形的基础知识,经历了针对图形的探究过程,知晓了平行四边形的边、角关系的结论,那么在此基础上的再次“观察、猜想、实验验证”就失去了其真正的意义,也很难激发学生的学习热情。
四、教学策略选择与设计
观察、猜想、实验验证。
五、教学重点及难点
重点:平行四边形的定义,平行四边形的性质,以及性质的应用.
2.难点:运用平行四边形的性质进行有关的论证和计算.
六、教学流程
课堂引入:
1.我们一起来观察下图中的竹篱笆格子和汽车的防护链,想一想它们是什么几何图形的形象?
平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
新授:
你能总结出平行四边形的定义吗?
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)表示:平行四边形用符号“”来表示.
如图,在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD记作“
ABCD”,读作“平行四边形ABCD”.
①∵AB//DC
,AD//BC
,
∴四边形ABCD是平行四边形(判定);
②∵四边形ABCD是平行四边形∴AB//DC,
AD//BC(性质).
注意:平行四边形中对边是指无公共点的边,对角是指不相邻的角,邻边是指有公共端点的边,邻角是指有一条公共边的两个角.而三角形对边是指一个角的对边,对角是指一条边的对角.(教学时要结合图形,让学生认识清楚)
【探究】
平行四边形是一种特殊的四边形,它除具有四边形的性质和两组对边分别平行外,还有什么特殊的性质呢?我们一起来探究一下.
让学生根据平行四边形的定义画一个一个平行四边形,观察这个四边形,它除具有四边形的性质和两组对边分别平行外以,它的边和角之间有什么关系?度量一下,是不是和你猜想的一致?
(1)由定义知道,平行四边形的对边平行.根据平行线的性质可知,在平行四边形中,相邻的角互为补角.
(相邻的角指四边形中有一条公共边的两个角.注意和第一章的邻角相区别.教学时结合图形使学生分辨清楚.)
(2)猜想
平行四边形的对边相等、对角相等.
下面证明这个结论的正确性.
已知:如图
ABCD,
求证:AB=CD,CB=AD,∠B=∠D,∠BAD=∠BCD.
分析:作
ABCD的对角线AC,它将平行四边形分成△ABC和△CDA,证明这两个三角形全等即可得到结论.
(作对角线是解决四边形问题常用的辅助线,通过作对角线,可以把未知问题转化为已知的关于三角形的问题.)
证明:连接AC,
∵
AB∥CD,AD∥BC,
∴
∠1=∠3,∠2=∠4.
又
AC=CA,
∴
△ABC≌△CDA
(ASA).
∴
AB=CD,CB=AD,∠B=∠D.
又
∠1+∠4=∠2+∠3,
∴
∠BAD=∠BCD.
由此得到:
平行四边形性质1 平行四边形的对边相等.
平行四边形性质2
平行四边形的对角相等.
例习题分析
例1(教材P42例1)
例2(补充)如图,在平行四边形ABCD中,AE=CF,求证:AF=CE.
分析:要证AF=CE,需证△ADF≌△CBE,由于四边形ABCD是平行四边形,因此有∠D=∠B
,AD=BC,AB=CD,又AE=CF,根据等式性质,可得BE=DF.由“边角边”可得出所需要的结论.证明略.
完成课本P42-43的内容学习
两条平行线之间的距离:
两条平行线中,一条直线上任意一点到另一条直线的距离。
【探究】
完成课本P43“探究”
从而可以得到:
平行四边形性质:平行四边形的对角线互相平分。
引导学生证明以上性质。
例(教材P94的例2)已知四边形ABCD是平行四边形,AB=10cm,AD=8cm,AC⊥BC,求BC、CD、AC、OA的长以及ABCD的面积.
分析:由平行四边形的对边相等,可得BC、CD的长,在Rt△ABC中,由勾股定理可得AC的长.再由平行四边形的对角线互相平分可求得OA的长,根据平行四边形的面积计算公式:平行四边形的面积=底×高(高为此底上的高),可求得ABCD的面积.(平行四边形的面积小学学过,再次强调“底”是对应着高说的,平行四边形中,任一边都可以作为“底”,“底”确定后,高也就随之确定了.)3.平行四边形的面积计算.
解题过程略
随堂练习
1.填空:
(1)在
ABCD中,∠A=
,则∠B=
度,∠C=
度,∠D=
度.
(2)如果
ABCD中,∠A—∠B=240,则∠A=
度,∠B=
度,∠C=
度,∠D=
度.
(3)如果
ABCD的周长为28cm,且AB:BC=2∶5,那么AB=
cm,BC=
cm,CD=
cm,CD=
cm.
2.如图4.3-9,在
ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足,求证:BE=DF.
课堂小结
本节课我们学习了哪些内容?
课后练习
1.课本练习及习题;
2.在
ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么图中的平行四边形一共有(
).
(A)4个
(B)5个
(C)8个
(D)9个
七、板书设计
1.标题
2.平行四边形的性质及推到;
3.性质的证明及例题;
八、教学反思
授课时间:
教研组检查情况:
组长签字:
年
月
日
教务处检查情况:
主任(教务员)签字:
年
月
日
1
