2020-2021学年黑龙江省哈尔滨市香坊区六年级(上)期末数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市香坊区六年级(上)期末数学试卷(五四学制)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 694.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览




文档简介
2020-2021学年黑龙江省哈尔滨市香坊区六年级(上)期末数学试卷(五四学制)
一、选择题(每小题3分).
1.分数的倒数是( )
A. B. C. D.
2.下列图案中是轴对称图形的是( )
A. B. C. D.
3.根据线段图列出的正确算式是( )
A.4000× B.4000
C.4000× D.4000
4.一种纺织品的合格率是98%,300件产品中有m件产品不合格,则m值为( )
A.2 B.4 C.6 D.8
5.甲数的80%等于乙数的50%(甲数与乙数都大于0),则( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
6.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( )
A.10πcm B.20πcm C.30πcm D.40πcm
7.在一幅比例尺是1:5000000的地图上,量得上海到杭州的距离是3.4cm.那么上海到杭州的实际距离是( )
A.17km B.34km C.170km D.340km
8.新兴商场出售一个A型和一个B型的吹风机,售价都是300元,同进价比,A型电吹风赚了20%,B型电吹风赔了20%,则新兴商场出售一个A型和一个B型电吹风后( )
A.盈利25元 B.赔了25元 C.不盈不亏 D.盈利50元
9.如果水冻成冰后体积增加10%,那么这些冰化成水后体积将减少( )
A.10% B. C. D.9%
10.下列说法:①书的单价一定,总价与订阅的数量成正比例;②圆的对称轴是直径所在的直线;③圆所占平面的大小叫做圆的面积;④圆锥的体积一定是圆柱体积的.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分).
11.把百分数27%化成小数是 .
12.要画一个半径是3cm的圆,则圆规两脚间的距离应是 cm.
13.甲乙两个数的比4:3,甲数是80,则乙数是 .
14.一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程为 cm.(π取3.14)
15.妈妈给奶奶汇2000元,邮局规定要交1%的汇费,则汇费是 元.
16.一列数:,,,,…,按照如此规律第六个数应是 .
17.童趣玩具店的玩具凭优惠卡可打八折,陈冬用优惠卡买了一个玩具,省了9.6元.这个玩具原价是 元.
18.我国发射的科学实验人造卫星,在空中绕地球运行6周需要10.6小时,运行15周要用 小时.
19.甲,乙二人分别从一条笔直的公路上的AB两地同时出发相向而行,甲每分钟走60米,乙每分钟走48米,5分钟后两人相距20米,则A.B两地之间的距离为 米.
20.一个圆锥和一个圆柱的底面积相等,已知圆柱的体积是圆锥的9倍,圆锥的高是8.1cm,则这个圆柱的高是 cm.
三.解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.计算:
(1)(+)×;
(2)(1.6﹣)×÷3.
22.(1)解方程:+x=;
(2)解比例:x:=22:.
23.网格中每个小正方形的边长为1,每个小正方形的顶点为格点,三角形和长方形的顶点都在格点上.
(1)在图1的网格中按2:1画出网格中三角形放大后的图形①;
(2)在图2的网格中按1:2画出网格中长方形缩小后的图形②;
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 .
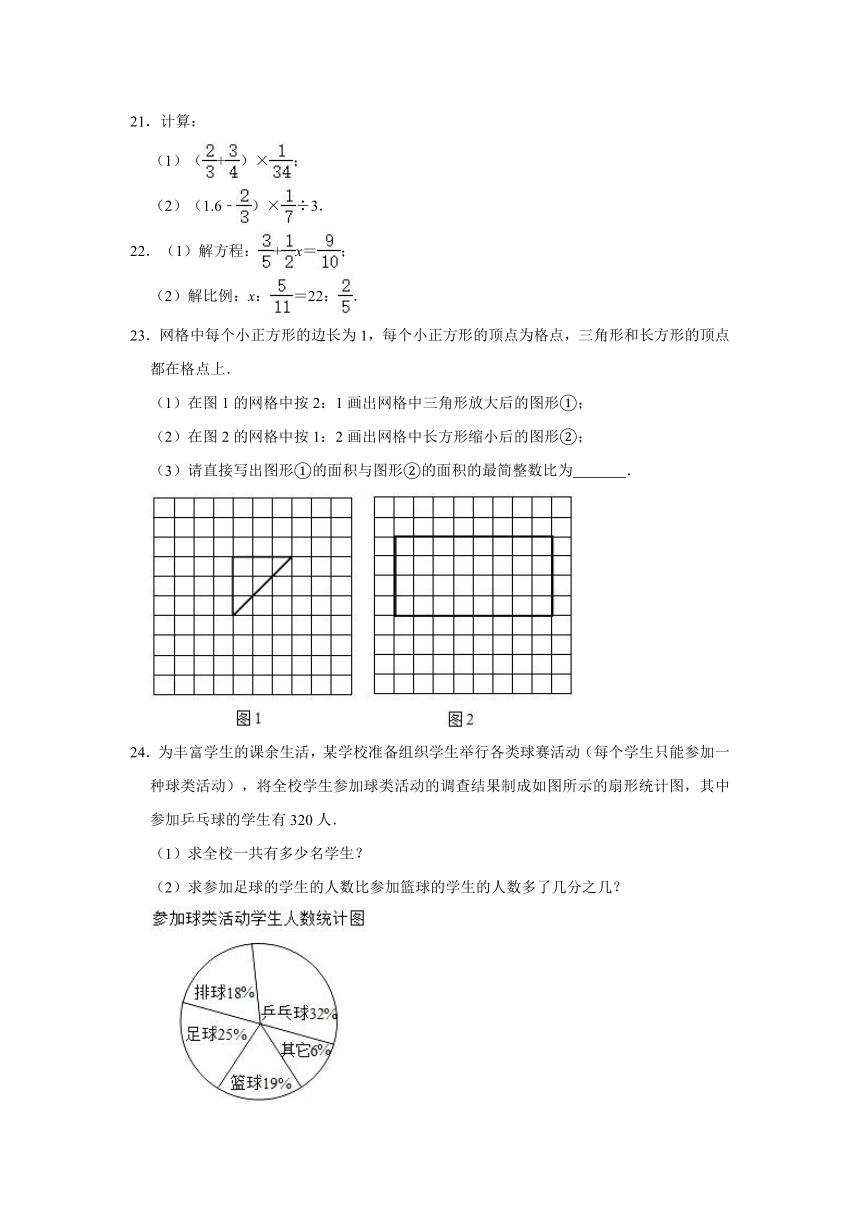
24.为丰富学生的课余生活,某学校准备组织学生举行各类球赛活动(每个学生只能参加一种球类活动),将全校学生参加球类活动的调查结果制成如图所示的扇形统计图,其中参加乒乓球的学生有320人.
(1)求全校一共有多少名学生?
(2)求参加足球的学生的人数比参加篮球的学生的人数多了几分之几?
25.某运动场正在建设中,运动场两端是半圆形,中间是长方形,长方形的长是100米,宽是80米(π值取3).
(1)求这个运动场的周长是多少米?
(2)已知这个运动场由草坪和塑胶跑道组成,塑胶跑道和草坪的面积比为1:7,每平方米塑胶的价格为600元,比每平方米草坪的价格高,若运动场铺满塑胶和草坪,求购买草坪所需要的费用是多少元?
26.某中学举行踢毽子比赛,六年一班组建了踢毽子训练小组,小组中男生有12人,女生人数与男生人数的比是5:6.
(1)求踢毽子小组的人数是多少人?
(2)踢毽子小组中男生人数占全班男生人数,踢毽子小组人数占全班人数的,求该班级未参加踢毽子的女生人数是多少人?
(3)由于活动的需要,未参加踢毽子训练的同学中有一些女生要参加训练,有一些参加训练的男生退出了训练,调整后踢毽子小组训练的总人数多了2人,踢毽子小组中男生人数为女生人数的,求调整前踢毽子小组中退出训练的男生的人数.
27.如图所示,甲地有一个圆锥形的沙堆,沙堆的底面积是56.52平方米,沙堆的高是2.5米,现在准备派出若干货车将甲地的这堆沙子运往乙地铺设公路,乙地公路的宽为5米.
(1)用这堆沙子在这条宽为5米的公路上铺设4厘米厚的路面,求铺设这条公路的长是多少米?
(2)一辆A型货车从乙地开往甲地,出发小时后,一辆B型货车同时从乙地出发开往甲地,当A型货车又行驶了小时到达甲地时,B型货车行驶的路程比乙、甲两地之间的路程的少0.5千米,已知B型货车每小时行驶的路程比A型货车每小时行驶的路程少,求B型货车每小时行驶了多少千米?
(3)在(2)的条件下,3辆A型货车和8辆B型货车同时从乙地出发,一次将沙子从甲地运回乙地,每辆A型货车装载沙子的满载量与每辆B型货车装载沙子的满载量的比为3:2,每辆A型货车装载1立方米沙子行驶1千米的费用为1.5元,每辆B型货车装载1立方米沙子行驶1千米的费用为1.2元,每辆B型货车的其它费用为100元,每辆A型货车的其它费用比B型货车多,已知A型货车均满载沙子,有7辆B型货车满载沙子,这时将沙子全部运回乙地的费用为1869.2元,求每辆A型货车装载沙子的满载量是多少立方米?(费用包括货车运载沙子的费用和其它费用)
参考答案
一、选择题(每小题3分).
1.分数的倒数是( )
A. B. C. D.
解:分数的倒数是.
故选:D.
2.下列图案中是轴对称图形的是( )
A. B. C. D.
解:A、不是轴对称图形,本选项错误;
B、是轴对称图形,本选项正确;
C、不是轴对称图形,本选项错误;
D、不是轴对称图形,本选项错误.
故选:B.
3.根据线段图列出的正确算式是( )
A.4000× B.4000
C.4000× D.4000
解:由题意可得,
计划产煤为:4000÷(1+),
故选:D.
4.一种纺织品的合格率是98%,300件产品中有m件产品不合格,则m值为( )
A.2 B.4 C.6 D.8
解:∵一种纺织品的合格率是98%,300件产品中有m件产品不合格,
∴m值为:300×98%=6.
故选:C.
5.甲数的80%等于乙数的50%(甲数与乙数都大于0),则( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
解:甲数是1,
所以乙数=80%÷50%=1.6,
1<1.6,
即甲数<乙数,
故选:B.
6.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( )
A.10πcm B.20πcm C.30πcm D.40πcm
解:六位朋友每相邻两人之间的弧长所对的圆心角度数为60°,半径为(110+10)cm,
∴l==40π;
故选:D.
7.在一幅比例尺是1:5000000的地图上,量得上海到杭州的距离是3.4cm.那么上海到杭州的实际距离是( )
A.17km B.34km C.170km D.340km
解:3.4÷
=3.4×5000000
=17000000(厘米),
17000000厘米=170千米.
答:上海到杭州的实际距离是170千米.
故选:C.
8.新兴商场出售一个A型和一个B型的吹风机,售价都是300元,同进价比,A型电吹风赚了20%,B型电吹风赔了20%,则新兴商场出售一个A型和一个B型电吹风后( )
A.盈利25元 B.赔了25元 C.不盈不亏 D.盈利50元
解:设一个A型吹风机的进价为x元,
由题意得(1+20%)x=300,
解得x=250;
设一个B型吹风机的进价为y元,
由题意得(1﹣20%)y=300,
解得y=375,
∴300×2﹣(250+375)=﹣25(元),
故新兴商场出售一个A型和一个B型电吹风后赔了25元,
故选:B.
9.如果水冻成冰后体积增加10%,那么这些冰化成水后体积将减少( )
A.10% B. C. D.9%
解:设水的体积为a,则冰的体积为a(1+10%),
故这些冰化成水后体积将减少=,
故选:B.
10.下列说法:①书的单价一定,总价与订阅的数量成正比例;②圆的对称轴是直径所在的直线;③圆所占平面的大小叫做圆的面积;④圆锥的体积一定是圆柱体积的.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
解:①书的单价一定,总价与订阅的数量成正比例,正确.
②圆的对称轴是直径所在的直线,正确.
③圆所占平面的大小叫做圆的面积,正确.
④圆锥的体积一定是圆柱体积的,错误,条件是同第,等高.
故选:C.
二、填空题(每小题3分,共计30分)
11.把百分数27%化成小数是 0.27 .
解:27%=0.27.
故答案为:0.27.
12.要画一个半径是3cm的圆,则圆规两脚间的距离应是 3 cm.
解:圆规两脚间的距离就是半径,由于半径为3cm,
因此圆规两脚间的距离应是3cm,
故答案为:3.
13.甲乙两个数的比4:3,甲数是80,则乙数是 60 .
解:设乙数为x,
则4:3=80:x,
解得x=60.
乙数是60.
故答案为:60.
14.一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程为 62.8 cm.(π取3.14)
解:2π×20×=20π≈62.8(cm),
故答案为:62.8.
15.妈妈给奶奶汇2000元,邮局规定要交1%的汇费,则汇费是 20 元.
解:2000×1%=20(元).
故答案为:20.
16.一列数:,,,,…,按照如此规律第六个数应是 .
解:∵一列数:,,,,…,
∴第6个数为:=,
故答案为:.
17.童趣玩具店的玩具凭优惠卡可打八折,陈冬用优惠卡买了一个玩具,省了9.6元.这个玩具原价是 48 元.
解:设这个玩具原价为x元,
x﹣0.8x=9.6,
∴x=48,
故答案为:48
18.我国发射的科学实验人造卫星,在空中绕地球运行6周需要10.6小时,运行15周要用 26.5 小时.
解:根据题意可得,
15×=26.5(小时).
故答案为:26.5.
19.甲,乙二人分别从一条笔直的公路上的AB两地同时出发相向而行,甲每分钟走60米,乙每分钟走48米,5分钟后两人相距20米,则A.B两地之间的距离为 520或560 米.
解:设A,B两点的距离为xm,
由题意得x+20=(60+48)×5或x﹣(60+48)×5=20,
解得x=520或560,
答:A.B两地之间的距离为520或560米,
故答案为520或560.
20.一个圆锥和一个圆柱的底面积相等,已知圆柱的体积是圆锥的9倍,圆锥的高是8.1cm,则这个圆柱的高是 24.3 cm.
解:设这个圆柱的高是xcm,圆锥和圆柱的底面积都为S,
根据题意得S?x=9××S×8.1,
解得x=24.3(cm),
即这个圆柱的高是24.3cm.
故答案为24.3.
三.解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.计算:
(1)(+)×;
(2)(1.6﹣)×÷3.
解:(1)(+)×
=()×
=×
=;
(2)(1.6﹣)×÷3
=()×
=()×
=×
=.
22.(1)解方程:+x=;
(2)解比例:x:=22:.
解:(1)去分母,可得:6+5x=9,
移项,合并同类项,可得:5x=3,
系数化为1,可得:x=0.6.
(2)∵x:=22:,
∴x=×22,
∴x=10,
解得x=25.
23.网格中每个小正方形的边长为1,每个小正方形的顶点为格点,三角形和长方形的顶点都在格点上.
(1)在图1的网格中按2:1画出网格中三角形放大后的图形①;
(2)在图2的网格中按1:2画出网格中长方形缩小后的图形②;
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 9:4 .
解:(1)如图1,
(2)如图2,
(3)图形①的面积与图形②的面积的最简整数比为9:4.
故答案为9:4.
24.为丰富学生的课余生活,某学校准备组织学生举行各类球赛活动(每个学生只能参加一种球类活动),将全校学生参加球类活动的调查结果制成如图所示的扇形统计图,其中参加乒乓球的学生有320人.
(1)求全校一共有多少名学生?
(2)求参加足球的学生的人数比参加篮球的学生的人数多了几分之几?
解:(1)320÷32%=1000(名),
答:全校一共有1000名学生;
(2)(25%﹣19%)÷19%=,
答:参加足球的学生的人数比参加篮球的学生的人数多了.
25.某运动场正在建设中,运动场两端是半圆形,中间是长方形,长方形的长是100米,宽是80米(π值取3).
(1)求这个运动场的周长是多少米?
(2)已知这个运动场由草坪和塑胶跑道组成,塑胶跑道和草坪的面积比为1:7,每平方米塑胶的价格为600元,比每平方米草坪的价格高,若运动场铺满塑胶和草坪,求购买草坪所需要的费用是多少元?
解:(1)π×80+100×2=3×80+200=440(米),
答:运动场的周长为440米;
(2)草坪的面积为[π×()2+100×80]×=11200(平方米),
草坪的单价为600÷(1+)=500(元),
铺草坪的费用为500×11200=5600000(元),
答:购买草坪所需要的费用是5600000元.
26.某中学举行踢毽子比赛,六年一班组建了踢毽子训练小组,小组中男生有12人,女生人数与男生人数的比是5:6.
(1)求踢毽子小组的人数是多少人?
(2)踢毽子小组中男生人数占全班男生人数,踢毽子小组人数占全班人数的,求该班级未参加踢毽子的女生人数是多少人?
(3)由于活动的需要,未参加踢毽子训练的同学中有一些女生要参加训练,有一些参加训练的男生退出了训练,调整后踢毽子小组训练的总人数多了2人,踢毽子小组中男生人数为女生人数的,求调整前踢毽子小组中退出训练的男生的人数.
解:(1)12÷6×5=20(人),
10+12=22(人).
故踢毽子小组的人数是22人;
(2)12÷=26(人),
22÷=50(人),
50﹣26﹣10=14(人).
故该班级未参加踢毽子的女生人数是14人;
(3)设调整前踢毽子小组中退出训练的男生的人数为x人,依题意有
12﹣x=(22+2)×,
解得x=2.
故调整前踢毽子小组中退出训练的男生的人数为2人.
27.如图所示,甲地有一个圆锥形的沙堆,沙堆的底面积是56.52平方米,沙堆的高是2.5米,现在准备派出若干货车将甲地的这堆沙子运往乙地铺设公路,乙地公路的宽为5米.
(1)用这堆沙子在这条宽为5米的公路上铺设4厘米厚的路面,求铺设这条公路的长是多少米?
(2)一辆A型货车从乙地开往甲地,出发小时后,一辆B型货车同时从乙地出发开往甲地,当A型货车又行驶了小时到达甲地时,B型货车行驶的路程比乙、甲两地之间的路程的少0.5千米,已知B型货车每小时行驶的路程比A型货车每小时行驶的路程少,求B型货车每小时行驶了多少千米?
(3)在(2)的条件下,3辆A型货车和8辆B型货车同时从乙地出发,一次将沙子从甲地运回乙地,每辆A型货车装载沙子的满载量与每辆B型货车装载沙子的满载量的比为3:2,每辆A型货车装载1立方米沙子行驶1千米的费用为1.5元,每辆B型货车装载1立方米沙子行驶1千米的费用为1.2元,每辆B型货车的其它费用为100元,每辆A型货车的其它费用比B型货车多,已知A型货车均满载沙子,有7辆B型货车满载沙子,这时将沙子全部运回乙地的费用为1869.2元,求每辆A型货车装载沙子的满载量是多少立方米?(费用包括货车运载沙子的费用和其它费用)
【解答】解(1)×56.52×2.5=47.1(立方米),
4厘米=0.04米,
47.1÷(5×0.04)=235.5(米);
答:铺设这条公路的长是235.5米.
(2)设B型货车每小时行驶了x千米.
根据题意得,x÷(1﹣)×(+)×﹣x=0.5,
解得,x=6;
答:B型货车每小时行驶了6千米.
(3)设每辆A型货车满载量为m立方米.
根据题意得,3m×1.5×10+(47.1﹣3m)×1.2×10+3×150+8×100=1869.2,
解得,m=6;
答:每辆A型货车装载沙子的满载量6立方米.
一、选择题(每小题3分).
1.分数的倒数是( )
A. B. C. D.
2.下列图案中是轴对称图形的是( )
A. B. C. D.
3.根据线段图列出的正确算式是( )
A.4000× B.4000
C.4000× D.4000
4.一种纺织品的合格率是98%,300件产品中有m件产品不合格,则m值为( )
A.2 B.4 C.6 D.8
5.甲数的80%等于乙数的50%(甲数与乙数都大于0),则( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
6.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( )
A.10πcm B.20πcm C.30πcm D.40πcm
7.在一幅比例尺是1:5000000的地图上,量得上海到杭州的距离是3.4cm.那么上海到杭州的实际距离是( )
A.17km B.34km C.170km D.340km
8.新兴商场出售一个A型和一个B型的吹风机,售价都是300元,同进价比,A型电吹风赚了20%,B型电吹风赔了20%,则新兴商场出售一个A型和一个B型电吹风后( )
A.盈利25元 B.赔了25元 C.不盈不亏 D.盈利50元
9.如果水冻成冰后体积增加10%,那么这些冰化成水后体积将减少( )
A.10% B. C. D.9%
10.下列说法:①书的单价一定,总价与订阅的数量成正比例;②圆的对称轴是直径所在的直线;③圆所占平面的大小叫做圆的面积;④圆锥的体积一定是圆柱体积的.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题3分).
11.把百分数27%化成小数是 .
12.要画一个半径是3cm的圆,则圆规两脚间的距离应是 cm.
13.甲乙两个数的比4:3,甲数是80,则乙数是 .
14.一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程为 cm.(π取3.14)
15.妈妈给奶奶汇2000元,邮局规定要交1%的汇费,则汇费是 元.
16.一列数:,,,,…,按照如此规律第六个数应是 .
17.童趣玩具店的玩具凭优惠卡可打八折,陈冬用优惠卡买了一个玩具,省了9.6元.这个玩具原价是 元.
18.我国发射的科学实验人造卫星,在空中绕地球运行6周需要10.6小时,运行15周要用 小时.
19.甲,乙二人分别从一条笔直的公路上的AB两地同时出发相向而行,甲每分钟走60米,乙每分钟走48米,5分钟后两人相距20米,则A.B两地之间的距离为 米.
20.一个圆锥和一个圆柱的底面积相等,已知圆柱的体积是圆锥的9倍,圆锥的高是8.1cm,则这个圆柱的高是 cm.
三.解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.计算:
(1)(+)×;
(2)(1.6﹣)×÷3.
22.(1)解方程:+x=;
(2)解比例:x:=22:.
23.网格中每个小正方形的边长为1,每个小正方形的顶点为格点,三角形和长方形的顶点都在格点上.
(1)在图1的网格中按2:1画出网格中三角形放大后的图形①;
(2)在图2的网格中按1:2画出网格中长方形缩小后的图形②;
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 .
24.为丰富学生的课余生活,某学校准备组织学生举行各类球赛活动(每个学生只能参加一种球类活动),将全校学生参加球类活动的调查结果制成如图所示的扇形统计图,其中参加乒乓球的学生有320人.
(1)求全校一共有多少名学生?
(2)求参加足球的学生的人数比参加篮球的学生的人数多了几分之几?
25.某运动场正在建设中,运动场两端是半圆形,中间是长方形,长方形的长是100米,宽是80米(π值取3).
(1)求这个运动场的周长是多少米?
(2)已知这个运动场由草坪和塑胶跑道组成,塑胶跑道和草坪的面积比为1:7,每平方米塑胶的价格为600元,比每平方米草坪的价格高,若运动场铺满塑胶和草坪,求购买草坪所需要的费用是多少元?
26.某中学举行踢毽子比赛,六年一班组建了踢毽子训练小组,小组中男生有12人,女生人数与男生人数的比是5:6.
(1)求踢毽子小组的人数是多少人?
(2)踢毽子小组中男生人数占全班男生人数,踢毽子小组人数占全班人数的,求该班级未参加踢毽子的女生人数是多少人?
(3)由于活动的需要,未参加踢毽子训练的同学中有一些女生要参加训练,有一些参加训练的男生退出了训练,调整后踢毽子小组训练的总人数多了2人,踢毽子小组中男生人数为女生人数的,求调整前踢毽子小组中退出训练的男生的人数.
27.如图所示,甲地有一个圆锥形的沙堆,沙堆的底面积是56.52平方米,沙堆的高是2.5米,现在准备派出若干货车将甲地的这堆沙子运往乙地铺设公路,乙地公路的宽为5米.
(1)用这堆沙子在这条宽为5米的公路上铺设4厘米厚的路面,求铺设这条公路的长是多少米?
(2)一辆A型货车从乙地开往甲地,出发小时后,一辆B型货车同时从乙地出发开往甲地,当A型货车又行驶了小时到达甲地时,B型货车行驶的路程比乙、甲两地之间的路程的少0.5千米,已知B型货车每小时行驶的路程比A型货车每小时行驶的路程少,求B型货车每小时行驶了多少千米?
(3)在(2)的条件下,3辆A型货车和8辆B型货车同时从乙地出发,一次将沙子从甲地运回乙地,每辆A型货车装载沙子的满载量与每辆B型货车装载沙子的满载量的比为3:2,每辆A型货车装载1立方米沙子行驶1千米的费用为1.5元,每辆B型货车装载1立方米沙子行驶1千米的费用为1.2元,每辆B型货车的其它费用为100元,每辆A型货车的其它费用比B型货车多,已知A型货车均满载沙子,有7辆B型货车满载沙子,这时将沙子全部运回乙地的费用为1869.2元,求每辆A型货车装载沙子的满载量是多少立方米?(费用包括货车运载沙子的费用和其它费用)
参考答案
一、选择题(每小题3分).
1.分数的倒数是( )
A. B. C. D.
解:分数的倒数是.
故选:D.
2.下列图案中是轴对称图形的是( )
A. B. C. D.
解:A、不是轴对称图形,本选项错误;
B、是轴对称图形,本选项正确;
C、不是轴对称图形,本选项错误;
D、不是轴对称图形,本选项错误.
故选:B.
3.根据线段图列出的正确算式是( )
A.4000× B.4000
C.4000× D.4000
解:由题意可得,
计划产煤为:4000÷(1+),
故选:D.
4.一种纺织品的合格率是98%,300件产品中有m件产品不合格,则m值为( )
A.2 B.4 C.6 D.8
解:∵一种纺织品的合格率是98%,300件产品中有m件产品不合格,
∴m值为:300×98%=6.
故选:C.
5.甲数的80%等于乙数的50%(甲数与乙数都大于0),则( )
A.甲数>乙数 B.甲数<乙数 C.甲数=乙数 D.无法确定
解:甲数是1,
所以乙数=80%÷50%=1.6,
1<1.6,
即甲数<乙数,
故选:B.
6.如图,六位朋友均匀的围坐在圆桌旁聚会,圆桌的半径为110cm,每人离桌边10cm,则图中相邻两人之间的圆弧的长(结果保留π)为( )
A.10πcm B.20πcm C.30πcm D.40πcm
解:六位朋友每相邻两人之间的弧长所对的圆心角度数为60°,半径为(110+10)cm,
∴l==40π;
故选:D.
7.在一幅比例尺是1:5000000的地图上,量得上海到杭州的距离是3.4cm.那么上海到杭州的实际距离是( )
A.17km B.34km C.170km D.340km
解:3.4÷
=3.4×5000000
=17000000(厘米),
17000000厘米=170千米.
答:上海到杭州的实际距离是170千米.
故选:C.
8.新兴商场出售一个A型和一个B型的吹风机,售价都是300元,同进价比,A型电吹风赚了20%,B型电吹风赔了20%,则新兴商场出售一个A型和一个B型电吹风后( )
A.盈利25元 B.赔了25元 C.不盈不亏 D.盈利50元
解:设一个A型吹风机的进价为x元,
由题意得(1+20%)x=300,
解得x=250;
设一个B型吹风机的进价为y元,
由题意得(1﹣20%)y=300,
解得y=375,
∴300×2﹣(250+375)=﹣25(元),
故新兴商场出售一个A型和一个B型电吹风后赔了25元,
故选:B.
9.如果水冻成冰后体积增加10%,那么这些冰化成水后体积将减少( )
A.10% B. C. D.9%
解:设水的体积为a,则冰的体积为a(1+10%),
故这些冰化成水后体积将减少=,
故选:B.
10.下列说法:①书的单价一定,总价与订阅的数量成正比例;②圆的对称轴是直径所在的直线;③圆所占平面的大小叫做圆的面积;④圆锥的体积一定是圆柱体积的.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
解:①书的单价一定,总价与订阅的数量成正比例,正确.
②圆的对称轴是直径所在的直线,正确.
③圆所占平面的大小叫做圆的面积,正确.
④圆锥的体积一定是圆柱体积的,错误,条件是同第,等高.
故选:C.
二、填空题(每小题3分,共计30分)
11.把百分数27%化成小数是 0.27 .
解:27%=0.27.
故答案为:0.27.
12.要画一个半径是3cm的圆,则圆规两脚间的距离应是 3 cm.
解:圆规两脚间的距离就是半径,由于半径为3cm,
因此圆规两脚间的距离应是3cm,
故答案为:3.
13.甲乙两个数的比4:3,甲数是80,则乙数是 60 .
解:设乙数为x,
则4:3=80:x,
解得x=60.
乙数是60.
故答案为:60.
14.一只挂钟的分针长20cm,经过30分钟后,分针的尖端所走的路程为 62.8 cm.(π取3.14)
解:2π×20×=20π≈62.8(cm),
故答案为:62.8.
15.妈妈给奶奶汇2000元,邮局规定要交1%的汇费,则汇费是 20 元.
解:2000×1%=20(元).
故答案为:20.
16.一列数:,,,,…,按照如此规律第六个数应是 .
解:∵一列数:,,,,…,
∴第6个数为:=,
故答案为:.
17.童趣玩具店的玩具凭优惠卡可打八折,陈冬用优惠卡买了一个玩具,省了9.6元.这个玩具原价是 48 元.
解:设这个玩具原价为x元,
x﹣0.8x=9.6,
∴x=48,
故答案为:48
18.我国发射的科学实验人造卫星,在空中绕地球运行6周需要10.6小时,运行15周要用 26.5 小时.
解:根据题意可得,
15×=26.5(小时).
故答案为:26.5.
19.甲,乙二人分别从一条笔直的公路上的AB两地同时出发相向而行,甲每分钟走60米,乙每分钟走48米,5分钟后两人相距20米,则A.B两地之间的距离为 520或560 米.
解:设A,B两点的距离为xm,
由题意得x+20=(60+48)×5或x﹣(60+48)×5=20,
解得x=520或560,
答:A.B两地之间的距离为520或560米,
故答案为520或560.
20.一个圆锥和一个圆柱的底面积相等,已知圆柱的体积是圆锥的9倍,圆锥的高是8.1cm,则这个圆柱的高是 24.3 cm.
解:设这个圆柱的高是xcm,圆锥和圆柱的底面积都为S,
根据题意得S?x=9××S×8.1,
解得x=24.3(cm),
即这个圆柱的高是24.3cm.
故答案为24.3.
三.解答题(其中21-25题各8分,26-27题各10分,共计60分)
21.计算:
(1)(+)×;
(2)(1.6﹣)×÷3.
解:(1)(+)×
=()×
=×
=;
(2)(1.6﹣)×÷3
=()×
=()×
=×
=.
22.(1)解方程:+x=;
(2)解比例:x:=22:.
解:(1)去分母,可得:6+5x=9,
移项,合并同类项,可得:5x=3,
系数化为1,可得:x=0.6.
(2)∵x:=22:,
∴x=×22,
∴x=10,
解得x=25.
23.网格中每个小正方形的边长为1,每个小正方形的顶点为格点,三角形和长方形的顶点都在格点上.
(1)在图1的网格中按2:1画出网格中三角形放大后的图形①;
(2)在图2的网格中按1:2画出网格中长方形缩小后的图形②;
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 9:4 .
解:(1)如图1,
(2)如图2,
(3)图形①的面积与图形②的面积的最简整数比为9:4.
故答案为9:4.
24.为丰富学生的课余生活,某学校准备组织学生举行各类球赛活动(每个学生只能参加一种球类活动),将全校学生参加球类活动的调查结果制成如图所示的扇形统计图,其中参加乒乓球的学生有320人.
(1)求全校一共有多少名学生?
(2)求参加足球的学生的人数比参加篮球的学生的人数多了几分之几?
解:(1)320÷32%=1000(名),
答:全校一共有1000名学生;
(2)(25%﹣19%)÷19%=,
答:参加足球的学生的人数比参加篮球的学生的人数多了.
25.某运动场正在建设中,运动场两端是半圆形,中间是长方形,长方形的长是100米,宽是80米(π值取3).
(1)求这个运动场的周长是多少米?
(2)已知这个运动场由草坪和塑胶跑道组成,塑胶跑道和草坪的面积比为1:7,每平方米塑胶的价格为600元,比每平方米草坪的价格高,若运动场铺满塑胶和草坪,求购买草坪所需要的费用是多少元?
解:(1)π×80+100×2=3×80+200=440(米),
答:运动场的周长为440米;
(2)草坪的面积为[π×()2+100×80]×=11200(平方米),
草坪的单价为600÷(1+)=500(元),
铺草坪的费用为500×11200=5600000(元),
答:购买草坪所需要的费用是5600000元.
26.某中学举行踢毽子比赛,六年一班组建了踢毽子训练小组,小组中男生有12人,女生人数与男生人数的比是5:6.
(1)求踢毽子小组的人数是多少人?
(2)踢毽子小组中男生人数占全班男生人数,踢毽子小组人数占全班人数的,求该班级未参加踢毽子的女生人数是多少人?
(3)由于活动的需要,未参加踢毽子训练的同学中有一些女生要参加训练,有一些参加训练的男生退出了训练,调整后踢毽子小组训练的总人数多了2人,踢毽子小组中男生人数为女生人数的,求调整前踢毽子小组中退出训练的男生的人数.
解:(1)12÷6×5=20(人),
10+12=22(人).
故踢毽子小组的人数是22人;
(2)12÷=26(人),
22÷=50(人),
50﹣26﹣10=14(人).
故该班级未参加踢毽子的女生人数是14人;
(3)设调整前踢毽子小组中退出训练的男生的人数为x人,依题意有
12﹣x=(22+2)×,
解得x=2.
故调整前踢毽子小组中退出训练的男生的人数为2人.
27.如图所示,甲地有一个圆锥形的沙堆,沙堆的底面积是56.52平方米,沙堆的高是2.5米,现在准备派出若干货车将甲地的这堆沙子运往乙地铺设公路,乙地公路的宽为5米.
(1)用这堆沙子在这条宽为5米的公路上铺设4厘米厚的路面,求铺设这条公路的长是多少米?
(2)一辆A型货车从乙地开往甲地,出发小时后,一辆B型货车同时从乙地出发开往甲地,当A型货车又行驶了小时到达甲地时,B型货车行驶的路程比乙、甲两地之间的路程的少0.5千米,已知B型货车每小时行驶的路程比A型货车每小时行驶的路程少,求B型货车每小时行驶了多少千米?
(3)在(2)的条件下,3辆A型货车和8辆B型货车同时从乙地出发,一次将沙子从甲地运回乙地,每辆A型货车装载沙子的满载量与每辆B型货车装载沙子的满载量的比为3:2,每辆A型货车装载1立方米沙子行驶1千米的费用为1.5元,每辆B型货车装载1立方米沙子行驶1千米的费用为1.2元,每辆B型货车的其它费用为100元,每辆A型货车的其它费用比B型货车多,已知A型货车均满载沙子,有7辆B型货车满载沙子,这时将沙子全部运回乙地的费用为1869.2元,求每辆A型货车装载沙子的满载量是多少立方米?(费用包括货车运载沙子的费用和其它费用)
【解答】解(1)×56.52×2.5=47.1(立方米),
4厘米=0.04米,
47.1÷(5×0.04)=235.5(米);
答:铺设这条公路的长是235.5米.
(2)设B型货车每小时行驶了x千米.
根据题意得,x÷(1﹣)×(+)×﹣x=0.5,
解得,x=6;
答:B型货车每小时行驶了6千米.
(3)设每辆A型货车满载量为m立方米.
根据题意得,3m×1.5×10+(47.1﹣3m)×1.2×10+3×150+8×100=1869.2,
解得,m=6;
答:每辆A型货车装载沙子的满载量6立方米.
同课章节目录
