2020-2021学年山东省菏泽市定陶区九年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年山东省菏泽市定陶区九年级(上)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 905.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览



文档简介
2020-2021学年山东省菏泽市定陶区九年级第一学期期末数学试卷
一、选择题(每小题3分)
1.下列多边形一定相似的是( )
A.两个平行四边形 B.两个菱形
C.两个矩形 D.两个正方形
2.如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则BD的值( )
A.2 B. C. D.5
3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
4.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
5.如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD?AC;③AD?BC=AB?BD;④AB?BC=AC?BD.其中单独能够判定△ABC∽△ADB的个数是( )
A.①② B.①②③ C.①②④ D.①②③④
6.已知方程x2﹣7x+10=0的两个根是等腰三角形的两边长,则这个等腰三角形的周长为( )
A.9 B.12 C.12或9 D.不能确定
7.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A.4 B.6 C.8 D.12
8.关于x的一元二次方程x2+2(m﹣1)x﹣2m=0的根的情况是( )
A.无法确定 B.有两个不相等的实数根
C.有两个相等的实数根 D.无实数根
9.某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x,则下面所列方程正确的是( )
A.90(1+x)2=144
B.90(1﹣x)2=144
C.90(1+2x)=144
D.90(1+x)+90(1+x)2=144﹣90
10.关于x的一元二次方程(a﹣1)x2﹣2x+3=0没有实数根,则整数a的最小值是( )
A.0 B.1 C.2 D.3
二、填空题(共24分)
11.2sin60°﹣tan60°+cos45°= .
12.已知y与x成反比例,且当x=﹣3时,y=4,则当x=6时,y的值为 .
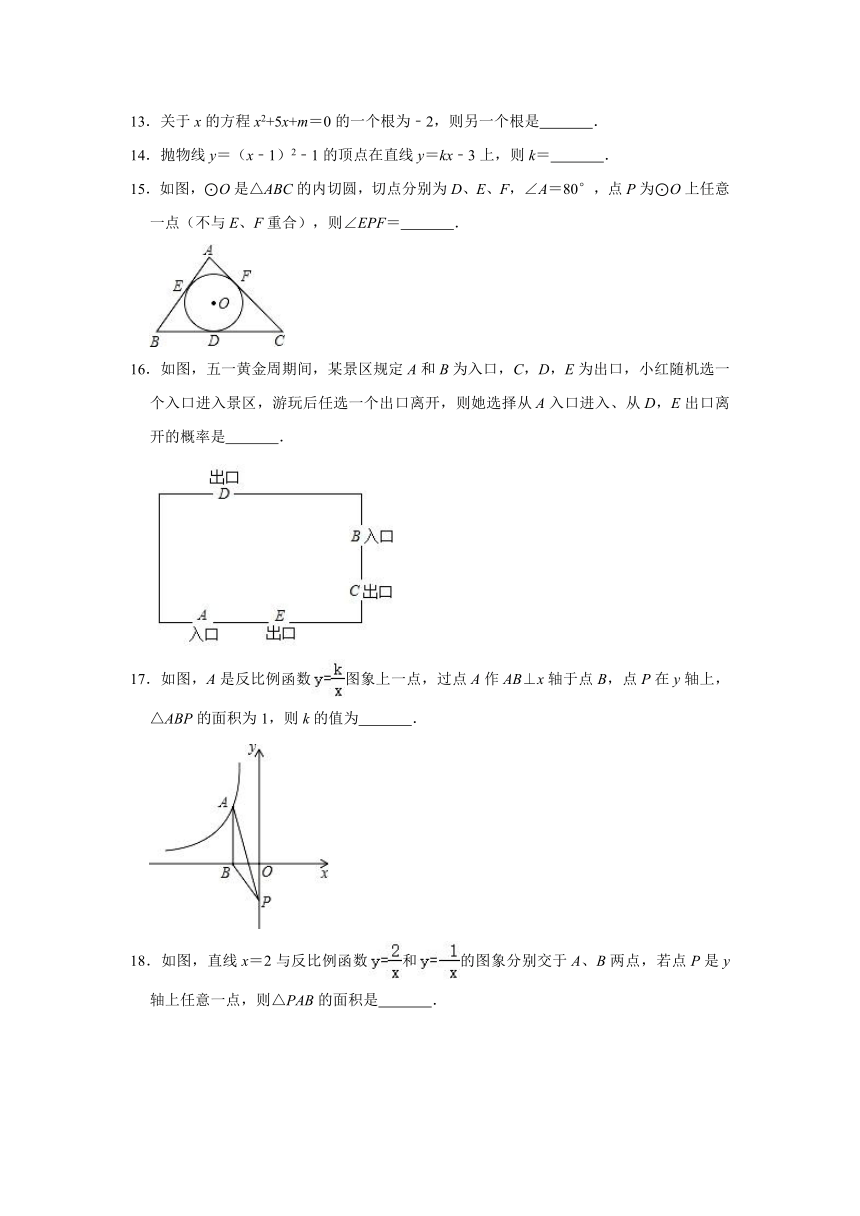
13.关于x的方程x2+5x+m=0的一个根为﹣2,则另一个根是 .
14.抛物线y=(x﹣1)2﹣1的顶点在直线y=kx﹣3上,则k= .
15.如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= .
16.如图,五一黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从D,E出口离开的概率是 .
17.如图,A是反比例函数图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为 .
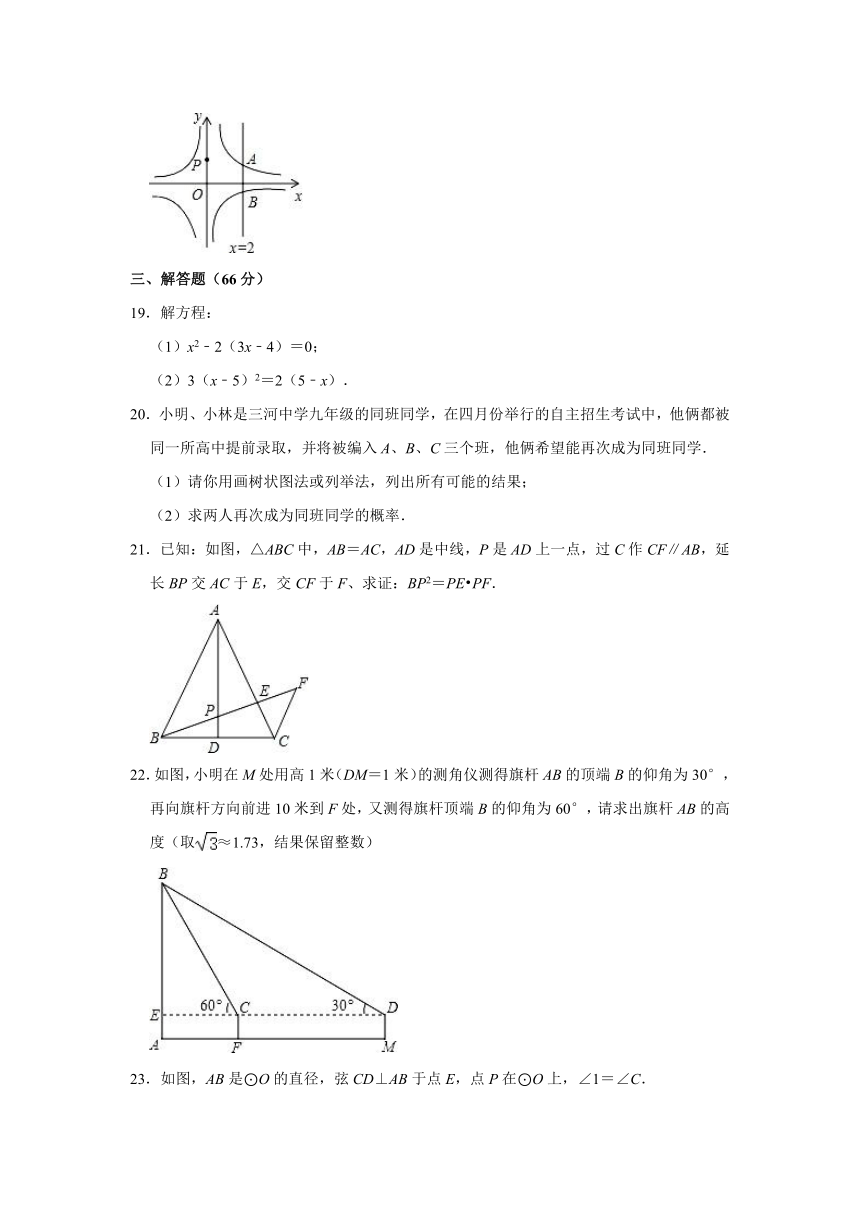
18.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
三、解答题(66分)
19.解方程:
(1)x2﹣2(3x﹣4)=0;
(2)3(x﹣5)2=2(5﹣x).
20.小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率.
21.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F、求证:BP2=PE?PF.
22.如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若BC=3,sin∠C=,求CD的长.
24.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且cos∠AOE=.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
25.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现.该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
26.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
参考答案
一、选择题(共30分)
1.下列多边形一定相似的是( )
A.两个平行四边形 B.两个菱形
C.两个矩形 D.两个正方形
【分析】利用相似多边形的对应边的比相等,对应角相等分析.
解:要判断两个多边形是否相似,需要看对应角是否相等,对应边的比是否相等.
矩形、菱形、平行四边形都属于形状不唯一确定的图形,即对应角、对应边的比不一定相等,故不一定相似,A、B、C错误;
而两个正方形,对应角都是90°,对应边的比也都相当,故一定相似,D正确.
故选:D.
2.如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则BD的值( )
A.2 B. C. D.5
【分析】直接利用菱形的性质结合锐角三角函数关系得出AD,AE的长,进而利用勾股定理得出BD的长.
解:∵四边形ABCD是菱形,
∴AD=AB,
∵DE⊥AB,cosA=,
∴设AE=3x,则AD=5x,故BE=2x,
∵BE=2,
∴x=1,故AB=AD=5,
则DE=4,
故BD==2.
故选:C.
3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
【分析】根据垂径定理得出=,=,根据以上结论判断即可.
解:A、根据垂径定理不能推出AC=AB,故A选项错误;
B、∵直径CD⊥弦AB,
∴=,
∵对的圆周角是∠C,对的圆心角是∠BOD,
∴∠BOD=2∠C,故B选项正确;
C、不能推出∠C=∠B,故C选项错误;
D、不能推出∠A=∠BOD,故D选项错误;
故选:B.
4.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
【分析】根据反比例函数的性质可以判断a、b的大小,从而可以解答本题.
解:∵y=﹣,
∴反比例函数y=﹣的图象位于第二、四象限,在每个象限内,y随x的增大而增大,
∵点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,
∴a<b<0,
故选:A.
5.如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD?AC;③AD?BC=AB?BD;④AB?BC=AC?BD.其中单独能够判定△ABC∽△ADB的个数是( )
A.①② B.①②③ C.①②④ D.①②③④
【分析】根据有两个角对应相等的三角形相似,可判断①,根据两边对应成比例且夹角相等的两个三角形相似,可判断断②③④.
解:①∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB;
②∵AB2=AD?AC,∴=,∠A=∠A,△ABC∽△ADB;
③∵AD?BC=AB?BD,∴=,∠A=∠A,△ABC与△ADB不相似;
④∵AB?BC=AC?BD,∴=,∠A=∠A,△ABC与△ADB不相似;
故选:A.
6.已知方程x2﹣7x+10=0的两个根是等腰三角形的两边长,则这个等腰三角形的周长为( )
A.9 B.12 C.12或9 D.不能确定
【分析】可先求得方程的两根,再根据等腰三角形的性质,结合三角形三边关系进行判断,再求得三角形的周长即可.
解:
解方程x2﹣7x+10=0可得x=2或x=5,
∴等腰三角形的两边长为2或5,
当底为2时,则等腰三角形的三边长为2、5、5,满足三角形三边关系,此时等腰三角形的周长为12;
当底为5时,则等腰三角形的三边长为5、2、2,2+2<5,不满足三角形三边关系;
∴等腰三角形的周长为12,
故选:B.
7.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A.4 B.6 C.8 D.12
【分析】根据三角形内角和定理可求得∠C=∠ABC=30°,再根据圆周角定理及直角三角形的性质即可求得BD的长.
解:∵∠BAC=120°,AB=AC=4
∴∠C=∠ABC=30°
∴∠D=30°
∵BD是直径
∴∠BAD=90°
∴BD=2AB=8.
故选:C.
8.关于x的一元二次方程x2+2(m﹣1)x﹣2m=0的根的情况是( )
A.无法确定 B.有两个不相等的实数根
C.有两个相等的实数根 D.无实数根
【分析】根据方程的系数结合根的判别式即可得出:△=[2(m﹣1)]2﹣4×(﹣2m)=4m2+2>0,即可判定方程有两个不相等的实数根.
解:∵△=[2(m﹣1)]2﹣4×(﹣2m)=4m2+2>0,
∴关于x的一元二次方程x2+2(m﹣1)x﹣2m=0有两个不相等的实数根.
故选:B.
9.某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x,则下面所列方程正确的是( )
A.90(1+x)2=144
B.90(1﹣x)2=144
C.90(1+2x)=144
D.90(1+x)+90(1+x)2=144﹣90
【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),由此可以求出第二个月和第三个月的营业额,而第一季度的总营业额已经知道,所以可以列出一个方程.
解:设平均每月营业额的增长率为x,
则第二个月的营业额为:90×(1+x),
第三个月的营业额为:90×(1+x)2,
则由题意列方程为:90(1+x)+90(1+x)2=144﹣90.
故选:D.
10.关于x的一元二次方程(a﹣1)x2﹣2x+3=0没有实数根,则整数a的最小值是( )
A.0 B.1 C.2 D.3
【分析】要使方程没有实根,只需二次项系数不等于0且根的判别式小于0,由此可求出a的范围,就可解决问题.
解:∵关于x的一元二次方程(a﹣1)x2﹣2x+3=0没有实数根,
∴a﹣1≠0且△<0,
∴a≠1且△=4﹣4×3×(a﹣1)<0,
∴a>且a≠1,
∴整数a的最小值是2.
故选:C.
二、填空题(共24分)
11.2sin60°﹣tan60°+cos45°= .
【分析】直接利用特殊角的三角函数值代入得出答案.
解:原式=2×﹣+×
=﹣+
=.
故答案为:.
12.已知y与x成反比例,且当x=﹣3时,y=4,则当x=6时,y的值为 ﹣2 .
【分析】根据待定系数法,可得反比例函数,根据自变量与函数值的对应关系,可得答案.
解:设反比例函数为y=,
当x=﹣3,y=4时,4=,解得k=﹣12.
反比例函数为y=.
当x=6时,y==﹣2,
故答案为:﹣2.
13.关于x的方程x2+5x+m=0的一个根为﹣2,则另一个根是 ﹣3 .
【分析】设另一根为x,利用根与系数的关系可求得x的值.
解:
设方程的另一根为x,
∵方程x2+5x+m=0的一个根为﹣2,
∴x+(﹣2)=﹣5,解得x=﹣3,
即方程的另一根是﹣3,
故答案为:﹣3.
14.抛物线y=(x﹣1)2﹣1的顶点在直线y=kx﹣3上,则k= 2 .
【分析】首先求出抛物线的顶点坐标,然后把顶点坐标代入y=kx﹣3,进而求出k的值.
解:∵抛物线解析式为y=(x﹣1)2﹣1,
∴抛物线的顶点坐标为(1,﹣1),
∵顶点在直线y=kx﹣3,
∴﹣1=k﹣3,
∴k=2.
故答案为2.
15.如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= 50°或130° .
【分析】有两种情况:①当P在弧EDF上时,连接OE、OF,求出∠EOF,根据圆周角定理求出即可;②当P在弧EMF上时,∠EPF=∠EMF,根据圆内接四边形的性质得到∠EMF+∠ENF=180°,代入求出即可.
解:有两种情况:
①当P在弧EDF上时,∠EPF=∠ENF,
连接OE、OF,
∵圆O是△ABC的内切圆,
∴OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
∵∠A=80°,
∴∠EOF=360°﹣∠AEO﹣∠AFO﹣∠A=100°,
∴∠ENF=∠EPF=∠EOF=50°,
②当P在弧EMF上时,∠EPF=∠EMF,
∠FPE=∠FME=180°﹣50°=130°,
故答案为:50°或130°.
16.如图,五一黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从D,E出口离开的概率是 .
【分析】画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
解:画树状图如图:
由树形图可知所有可能的结果有6种,小红从入口A进入景区并从D,E出口离开的结果数为2,
所以她选择从A入口进入、从D,E出口离开的概率是=,
故答案为:.
17.如图,A是反比例函数图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为 ﹣2 .
【分析】连接OA,作AC⊥y轴于C点,由于AB⊥x轴,则AB∥OP,根据同底等高的三角形面积相等得到S△OAB=S△PAB=1,则有S矩形ABOC=2S△OAB=2,根据k的几何意义得到|k|=2,即k=2或k=﹣2,然后根据反比例函数性质即可得到k=﹣2.
解:连接OA,作AC⊥y轴于C点,如图
∵AB⊥x轴,
∴AB∥OP,
∴S△OAB=S△PAB=1,
∴S矩形ABOC=2S△OAB=2,
∴|k|=2,即k=2或k=﹣2,
∵反比例函数图象过第二象限,
∴k=﹣2.
故答案为﹣2.
18.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
【分析】先分别求出A、B两点的坐标,得到AB的长度,再根据三角形的面积公式即可得出△PAB的面积.
解:∵把x=2分别代入、,得y=1、y=﹣.
∴A(2,1),B(2,﹣),
∴AB=1﹣(﹣)=.
∵P为y轴上的任意一点,
∴点P到直线x=2的距离为2,
∴△PAB的面积=AB×2=AB=.
故答案是:.
三、解答题(66分)
19.解方程:
(1)x2﹣2(3x﹣4)=0;
(2)3(x﹣5)2=2(5﹣x).
【分析】(1)整理为一般式,再利用因式分解法求解即可;
(2)利用因式分解法求解即可.
解:(1)整理,得:x2﹣6x+8=0,
∴(x﹣2)(x﹣4)=0,
则x﹣2=0或x﹣4=0,
解得x1=4,x2=2;
(2)∵3(x﹣5)2=2(5﹣x),
∴3(x﹣5)2+2(x﹣5)=0,
∴(x﹣5)(3x﹣13)=0,
∴x﹣5=0或3x﹣13=0,
解得x1=5,.
20.小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率.
【分析】(1)画树状图法或列举法,即可得到所有可能的结果;
(2)由(1)可知两人再次成为同班同学的概率.
解:
(1)画树状图如下:
由树形图可知所以可能的结果为AA,AB,AC,BA,BB,BC,CA,CB,CC;
(2)由(1)可知两人再次成为同班同学的概率==.
21.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F、求证:BP2=PE?PF.
【分析】要证线段乘积式相等,常常先证比例式成立,要证比例式,须有三角形相似,要证三角形相似,须根据已知与图形找条件就可.
【解答】证明:连接PC,
∵AB=AC,AD是中线,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
∵CF∥AB,∴∠PFC=∠ABP(两直线平行,内错角相等),
∴∠PCE=∠PFC.
又∵∠CPE=∠EPC,
∴△EPC∽△CPF.
∴(相似三角形的对应边成比例).
∴PC2=PE?PF.
∵PC=BP
∴BP2=PE?PF.
22.如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)
【分析】首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造边角关系,进而可求出答案.
解:∵∠BDE=30°,∠BCE=60°,
∴∠CBD=60°﹣∠BDE=30°=∠BDE,
∴BC=CD=10米,
在Rt△BCE中,sin60°=,即=,
解得BE=5米,
AB=BE+AE=5+1≈10米.
答:旗杆AB的高度大约是10米.
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若BC=3,sin∠C=,求CD的长.
【分析】(1)欲证明CB∥PD,只要证明∠1=∠P即可.
(2)根据三角函数的定义求出BE,再利用勾股定理求出EC可得结论.
【解答】(1)证明:∵∠C=∠P,
又∵∠1=∠C,
∴∠1=∠P,
∴CB∥PD.
(2)解:连接AC.
∵AB为⊙O的直径,
∴∠ACB=90°,
又∵CD⊥AB,
∴,
∴∠P=∠CAB,
∴=,
又∵BC=3,
∴BE=2,
∴CE===,
∴CD=2EC=2.
24.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且cos∠AOE=.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
【分析】(1)过A点作AD⊥OE,垂足为D,已知OA=5,cos∠AOE=,解直角三角形求OD、AD,确定A点坐标,根据A点坐标求反比例函数和B点坐标,根据A、B两点坐标,求一次函数的解析式;
(2)根据直线AB的解析式求C点坐标,再求△AOC的面积.
解:(1)过A点作AD⊥OE,垂足为D,
在Rt△AOD中,∵OA=5,cos∠AOE=,
∴OD=OA?cos∠AOE=3,
由勾股定理,得AD=4,
则A(﹣3,4),
∵A、B两点在反比例函数(m≠0)的图象上,
∴m=﹣3×4=6n,
解得m=﹣12,n=﹣2,
将A(﹣3,4),B(6,﹣2)代入y=kx+b中,得,
解得,
故反比例函数解析式为y=﹣,一次函数解析式为y=﹣x+2;
(2)在一次函数y=﹣x+2中,令y=0,得x=3,故C(3,0),
OC=3,S△AOC=×OC×AD=×3×4=6.
25.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现.该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
【分析】(1)根据总利润=每个利润×销售量可得函数解析式;
(2)将所得函数解析式配方成顶点式即可.
解:(1)根据题意可得:w=(x﹣20)y
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
w与x的函数关系式为:w=﹣2x2+120x﹣1600;
(2)根据题意可得:w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w有最大值.w最大值为200.
答:销售单价定为30元时,每天销售利润最大,最大销售利润200元.
26.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
【分析】(1)利用待定系数法求二次函数解析式;
(2)利用对称的性质得∠E′CP=∠ECP,E′C=CE,E′P=EP,由PE∥E′C得∠EPC=∠E′CP,则∠EPC=∠ECP,于是可判断EP=EC,所以EC=EP=PE′=E′C,则根据菱形的判定方法得到四边形EPE′C为菱形;
(3)先利用待定系数法求出直线BC的解析式为y=﹣x+8,根据二次函数和一次函数图象上点的坐标特征,设P(x,﹣x2+x+8),则E(x,﹣x+8),则可计算出PE=﹣x2+x+8﹣(﹣x+8)=﹣x2+4x,过点E作EF⊥y轴于点F,如图,证明△CFE∽△COB,利用相似比可计算出CE=x,则可利用EC=EP得到方程﹣x2+4x=x,然后解方程求出x即可得到P点坐标.
解:(1)把点C(0,8),B(6,0)代入在抛物线y=﹣x2+bx+c得,解得,
所以抛物线的表达式为y=﹣x2+x+8;
(2)以P,C,E,E′为顶点的四边形为菱形.理由如下:
∵E点和E′点关于直线PC对称,
∴∠E′CP=∠ECP,E′C=CE,E′P=EP,
又∵PD⊥x轴,
∴PE∥E′C,
∴∠EPC=∠E′CP,
∴∠EPC=∠ECP,
∴EP=EC,
∴EC=EP=PE′=E′C,
∴四边形EPE′C为菱形,
(3)设直线BC的解析式为y=kx+m,
把B(6,0),C(0,8)代入得,解得,
∴直线BC的解析式为y=﹣x+8;
设P(x,﹣x2+x+8),则E(x,﹣x+8),
∴PE=﹣x2+x+8﹣(﹣x+8)=﹣x2+4x,
过点E作EF⊥y轴于点F,如图,
在Rt△OBC中,BC==10,
∵EF∥OB,
∴△CFE∽△COB,
∴=,即=,
∴CE=x,
∵EC=EP,
∴﹣x2+4x=x,
整理得2x2﹣7x=0,解得x1=0(舍去),x2=,
∴点P的坐标为(,).
一、选择题(每小题3分)
1.下列多边形一定相似的是( )
A.两个平行四边形 B.两个菱形
C.两个矩形 D.两个正方形
2.如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则BD的值( )
A.2 B. C. D.5
3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
4.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
5.如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD?AC;③AD?BC=AB?BD;④AB?BC=AC?BD.其中单独能够判定△ABC∽△ADB的个数是( )
A.①② B.①②③ C.①②④ D.①②③④
6.已知方程x2﹣7x+10=0的两个根是等腰三角形的两边长,则这个等腰三角形的周长为( )
A.9 B.12 C.12或9 D.不能确定
7.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A.4 B.6 C.8 D.12
8.关于x的一元二次方程x2+2(m﹣1)x﹣2m=0的根的情况是( )
A.无法确定 B.有两个不相等的实数根
C.有两个相等的实数根 D.无实数根
9.某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x,则下面所列方程正确的是( )
A.90(1+x)2=144
B.90(1﹣x)2=144
C.90(1+2x)=144
D.90(1+x)+90(1+x)2=144﹣90
10.关于x的一元二次方程(a﹣1)x2﹣2x+3=0没有实数根,则整数a的最小值是( )
A.0 B.1 C.2 D.3
二、填空题(共24分)
11.2sin60°﹣tan60°+cos45°= .
12.已知y与x成反比例,且当x=﹣3时,y=4,则当x=6时,y的值为 .
13.关于x的方程x2+5x+m=0的一个根为﹣2,则另一个根是 .
14.抛物线y=(x﹣1)2﹣1的顶点在直线y=kx﹣3上,则k= .
15.如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= .
16.如图,五一黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从D,E出口离开的概率是 .
17.如图,A是反比例函数图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为 .
18.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
三、解答题(66分)
19.解方程:
(1)x2﹣2(3x﹣4)=0;
(2)3(x﹣5)2=2(5﹣x).
20.小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率.
21.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F、求证:BP2=PE?PF.
22.如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若BC=3,sin∠C=,求CD的长.
24.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且cos∠AOE=.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
25.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现.该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
26.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
参考答案
一、选择题(共30分)
1.下列多边形一定相似的是( )
A.两个平行四边形 B.两个菱形
C.两个矩形 D.两个正方形
【分析】利用相似多边形的对应边的比相等,对应角相等分析.
解:要判断两个多边形是否相似,需要看对应角是否相等,对应边的比是否相等.
矩形、菱形、平行四边形都属于形状不唯一确定的图形,即对应角、对应边的比不一定相等,故不一定相似,A、B、C错误;
而两个正方形,对应角都是90°,对应边的比也都相当,故一定相似,D正确.
故选:D.
2.如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则BD的值( )
A.2 B. C. D.5
【分析】直接利用菱形的性质结合锐角三角函数关系得出AD,AE的长,进而利用勾股定理得出BD的长.
解:∵四边形ABCD是菱形,
∴AD=AB,
∵DE⊥AB,cosA=,
∴设AE=3x,则AD=5x,故BE=2x,
∵BE=2,
∴x=1,故AB=AD=5,
则DE=4,
故BD==2.
故选:C.
3.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
【分析】根据垂径定理得出=,=,根据以上结论判断即可.
解:A、根据垂径定理不能推出AC=AB,故A选项错误;
B、∵直径CD⊥弦AB,
∴=,
∵对的圆周角是∠C,对的圆心角是∠BOD,
∴∠BOD=2∠C,故B选项正确;
C、不能推出∠C=∠B,故C选项错误;
D、不能推出∠A=∠BOD,故D选项错误;
故选:B.
4.a、b是实数,点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,则( )
A.a<b<0 B.b<a<0 C.a<0<b D.b<0<a
【分析】根据反比例函数的性质可以判断a、b的大小,从而可以解答本题.
解:∵y=﹣,
∴反比例函数y=﹣的图象位于第二、四象限,在每个象限内,y随x的增大而增大,
∵点A(2,a)、B(3,b)在反比例函数y=﹣的图象上,
∴a<b<0,
故选:A.
5.如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=AD?AC;③AD?BC=AB?BD;④AB?BC=AC?BD.其中单独能够判定△ABC∽△ADB的个数是( )
A.①② B.①②③ C.①②④ D.①②③④
【分析】根据有两个角对应相等的三角形相似,可判断①,根据两边对应成比例且夹角相等的两个三角形相似,可判断断②③④.
解:①∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB;
②∵AB2=AD?AC,∴=,∠A=∠A,△ABC∽△ADB;
③∵AD?BC=AB?BD,∴=,∠A=∠A,△ABC与△ADB不相似;
④∵AB?BC=AC?BD,∴=,∠A=∠A,△ABC与△ADB不相似;
故选:A.
6.已知方程x2﹣7x+10=0的两个根是等腰三角形的两边长,则这个等腰三角形的周长为( )
A.9 B.12 C.12或9 D.不能确定
【分析】可先求得方程的两根,再根据等腰三角形的性质,结合三角形三边关系进行判断,再求得三角形的周长即可.
解:
解方程x2﹣7x+10=0可得x=2或x=5,
∴等腰三角形的两边长为2或5,
当底为2时,则等腰三角形的三边长为2、5、5,满足三角形三边关系,此时等腰三角形的周长为12;
当底为5时,则等腰三角形的三边长为5、2、2,2+2<5,不满足三角形三边关系;
∴等腰三角形的周长为12,
故选:B.
7.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A.4 B.6 C.8 D.12
【分析】根据三角形内角和定理可求得∠C=∠ABC=30°,再根据圆周角定理及直角三角形的性质即可求得BD的长.
解:∵∠BAC=120°,AB=AC=4
∴∠C=∠ABC=30°
∴∠D=30°
∵BD是直径
∴∠BAD=90°
∴BD=2AB=8.
故选:C.
8.关于x的一元二次方程x2+2(m﹣1)x﹣2m=0的根的情况是( )
A.无法确定 B.有两个不相等的实数根
C.有两个相等的实数根 D.无实数根
【分析】根据方程的系数结合根的判别式即可得出:△=[2(m﹣1)]2﹣4×(﹣2m)=4m2+2>0,即可判定方程有两个不相等的实数根.
解:∵△=[2(m﹣1)]2﹣4×(﹣2m)=4m2+2>0,
∴关于x的一元二次方程x2+2(m﹣1)x﹣2m=0有两个不相等的实数根.
故选:B.
9.某超市1月份营业额为90万元,1月、2月、3月总营业额为144万元,设平均每月营业额增长率为x,则下面所列方程正确的是( )
A.90(1+x)2=144
B.90(1﹣x)2=144
C.90(1+2x)=144
D.90(1+x)+90(1+x)2=144﹣90
【分析】增长率问题,一般用增长后的量=增长前的量×(1+增长率),由此可以求出第二个月和第三个月的营业额,而第一季度的总营业额已经知道,所以可以列出一个方程.
解:设平均每月营业额的增长率为x,
则第二个月的营业额为:90×(1+x),
第三个月的营业额为:90×(1+x)2,
则由题意列方程为:90(1+x)+90(1+x)2=144﹣90.
故选:D.
10.关于x的一元二次方程(a﹣1)x2﹣2x+3=0没有实数根,则整数a的最小值是( )
A.0 B.1 C.2 D.3
【分析】要使方程没有实根,只需二次项系数不等于0且根的判别式小于0,由此可求出a的范围,就可解决问题.
解:∵关于x的一元二次方程(a﹣1)x2﹣2x+3=0没有实数根,
∴a﹣1≠0且△<0,
∴a≠1且△=4﹣4×3×(a﹣1)<0,
∴a>且a≠1,
∴整数a的最小值是2.
故选:C.
二、填空题(共24分)
11.2sin60°﹣tan60°+cos45°= .
【分析】直接利用特殊角的三角函数值代入得出答案.
解:原式=2×﹣+×
=﹣+
=.
故答案为:.
12.已知y与x成反比例,且当x=﹣3时,y=4,则当x=6时,y的值为 ﹣2 .
【分析】根据待定系数法,可得反比例函数,根据自变量与函数值的对应关系,可得答案.
解:设反比例函数为y=,
当x=﹣3,y=4时,4=,解得k=﹣12.
反比例函数为y=.
当x=6时,y==﹣2,
故答案为:﹣2.
13.关于x的方程x2+5x+m=0的一个根为﹣2,则另一个根是 ﹣3 .
【分析】设另一根为x,利用根与系数的关系可求得x的值.
解:
设方程的另一根为x,
∵方程x2+5x+m=0的一个根为﹣2,
∴x+(﹣2)=﹣5,解得x=﹣3,
即方程的另一根是﹣3,
故答案为:﹣3.
14.抛物线y=(x﹣1)2﹣1的顶点在直线y=kx﹣3上,则k= 2 .
【分析】首先求出抛物线的顶点坐标,然后把顶点坐标代入y=kx﹣3,进而求出k的值.
解:∵抛物线解析式为y=(x﹣1)2﹣1,
∴抛物线的顶点坐标为(1,﹣1),
∵顶点在直线y=kx﹣3,
∴﹣1=k﹣3,
∴k=2.
故答案为2.
15.如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠A=80°,点P为⊙O上任意一点(不与E、F重合),则∠EPF= 50°或130° .
【分析】有两种情况:①当P在弧EDF上时,连接OE、OF,求出∠EOF,根据圆周角定理求出即可;②当P在弧EMF上时,∠EPF=∠EMF,根据圆内接四边形的性质得到∠EMF+∠ENF=180°,代入求出即可.
解:有两种情况:
①当P在弧EDF上时,∠EPF=∠ENF,
连接OE、OF,
∵圆O是△ABC的内切圆,
∴OE⊥AB,OF⊥AC,
∴∠AEO=∠AFO=90°,
∵∠A=80°,
∴∠EOF=360°﹣∠AEO﹣∠AFO﹣∠A=100°,
∴∠ENF=∠EPF=∠EOF=50°,
②当P在弧EMF上时,∠EPF=∠EMF,
∠FPE=∠FME=180°﹣50°=130°,
故答案为:50°或130°.
16.如图,五一黄金周期间,某景区规定A和B为入口,C,D,E为出口,小红随机选一个入口进入景区,游玩后任选一个出口离开,则她选择从A入口进入、从D,E出口离开的概率是 .
【分析】画树状图得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式求解即可.
解:画树状图如图:
由树形图可知所有可能的结果有6种,小红从入口A进入景区并从D,E出口离开的结果数为2,
所以她选择从A入口进入、从D,E出口离开的概率是=,
故答案为:.
17.如图,A是反比例函数图象上一点,过点A作AB⊥x轴于点B,点P在y轴上,△ABP的面积为1,则k的值为 ﹣2 .
【分析】连接OA,作AC⊥y轴于C点,由于AB⊥x轴,则AB∥OP,根据同底等高的三角形面积相等得到S△OAB=S△PAB=1,则有S矩形ABOC=2S△OAB=2,根据k的几何意义得到|k|=2,即k=2或k=﹣2,然后根据反比例函数性质即可得到k=﹣2.
解:连接OA,作AC⊥y轴于C点,如图
∵AB⊥x轴,
∴AB∥OP,
∴S△OAB=S△PAB=1,
∴S矩形ABOC=2S△OAB=2,
∴|k|=2,即k=2或k=﹣2,
∵反比例函数图象过第二象限,
∴k=﹣2.
故答案为﹣2.
18.如图,直线x=2与反比例函数和的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是 .
【分析】先分别求出A、B两点的坐标,得到AB的长度,再根据三角形的面积公式即可得出△PAB的面积.
解:∵把x=2分别代入、,得y=1、y=﹣.
∴A(2,1),B(2,﹣),
∴AB=1﹣(﹣)=.
∵P为y轴上的任意一点,
∴点P到直线x=2的距离为2,
∴△PAB的面积=AB×2=AB=.
故答案是:.
三、解答题(66分)
19.解方程:
(1)x2﹣2(3x﹣4)=0;
(2)3(x﹣5)2=2(5﹣x).
【分析】(1)整理为一般式,再利用因式分解法求解即可;
(2)利用因式分解法求解即可.
解:(1)整理,得:x2﹣6x+8=0,
∴(x﹣2)(x﹣4)=0,
则x﹣2=0或x﹣4=0,
解得x1=4,x2=2;
(2)∵3(x﹣5)2=2(5﹣x),
∴3(x﹣5)2+2(x﹣5)=0,
∴(x﹣5)(3x﹣13)=0,
∴x﹣5=0或3x﹣13=0,
解得x1=5,.
20.小明、小林是三河中学九年级的同班同学,在四月份举行的自主招生考试中,他俩都被同一所高中提前录取,并将被编入A、B、C三个班,他俩希望能再次成为同班同学.
(1)请你用画树状图法或列举法,列出所有可能的结果;
(2)求两人再次成为同班同学的概率.
【分析】(1)画树状图法或列举法,即可得到所有可能的结果;
(2)由(1)可知两人再次成为同班同学的概率.
解:
(1)画树状图如下:
由树形图可知所以可能的结果为AA,AB,AC,BA,BB,BC,CA,CB,CC;
(2)由(1)可知两人再次成为同班同学的概率==.
21.已知:如图,△ABC中,AB=AC,AD是中线,P是AD上一点,过C作CF∥AB,延长BP交AC于E,交CF于F、求证:BP2=PE?PF.
【分析】要证线段乘积式相等,常常先证比例式成立,要证比例式,须有三角形相似,要证三角形相似,须根据已知与图形找条件就可.
【解答】证明:连接PC,
∵AB=AC,AD是中线,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
∵CF∥AB,∴∠PFC=∠ABP(两直线平行,内错角相等),
∴∠PCE=∠PFC.
又∵∠CPE=∠EPC,
∴△EPC∽△CPF.
∴(相似三角形的对应边成比例).
∴PC2=PE?PF.
∵PC=BP
∴BP2=PE?PF.
22.如图,小明在M处用高1米(DM=1米)的测角仪测得旗杆AB的顶端B的仰角为30°,再向旗杆方向前进10米到F处,又测得旗杆顶端B的仰角为60°,请求出旗杆AB的高度(取≈1.73,结果保留整数)
【分析】首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造边角关系,进而可求出答案.
解:∵∠BDE=30°,∠BCE=60°,
∴∠CBD=60°﹣∠BDE=30°=∠BDE,
∴BC=CD=10米,
在Rt△BCE中,sin60°=,即=,
解得BE=5米,
AB=BE+AE=5+1≈10米.
答:旗杆AB的高度大约是10米.
23.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
(1)求证:CB∥PD;
(2)若BC=3,sin∠C=,求CD的长.
【分析】(1)欲证明CB∥PD,只要证明∠1=∠P即可.
(2)根据三角函数的定义求出BE,再利用勾股定理求出EC可得结论.
【解答】(1)证明:∵∠C=∠P,
又∵∠1=∠C,
∴∠1=∠P,
∴CB∥PD.
(2)解:连接AC.
∵AB为⊙O的直径,
∴∠ACB=90°,
又∵CD⊥AB,
∴,
∴∠P=∠CAB,
∴=,
又∵BC=3,
∴BE=2,
∴CE===,
∴CD=2EC=2.
24.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n).线段OA=5,E为x轴上一点,且cos∠AOE=.
(1)求该反比例函数和一次函数的解析式;
(2)求△AOC的面积.
【分析】(1)过A点作AD⊥OE,垂足为D,已知OA=5,cos∠AOE=,解直角三角形求OD、AD,确定A点坐标,根据A点坐标求反比例函数和B点坐标,根据A、B两点坐标,求一次函数的解析式;
(2)根据直线AB的解析式求C点坐标,再求△AOC的面积.
解:(1)过A点作AD⊥OE,垂足为D,
在Rt△AOD中,∵OA=5,cos∠AOE=,
∴OD=OA?cos∠AOE=3,
由勾股定理,得AD=4,
则A(﹣3,4),
∵A、B两点在反比例函数(m≠0)的图象上,
∴m=﹣3×4=6n,
解得m=﹣12,n=﹣2,
将A(﹣3,4),B(6,﹣2)代入y=kx+b中,得,
解得,
故反比例函数解析式为y=﹣,一次函数解析式为y=﹣x+2;
(2)在一次函数y=﹣x+2中,令y=0,得x=3,故C(3,0),
OC=3,S△AOC=×OC×AD=×3×4=6.
25.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现.该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
【分析】(1)根据总利润=每个利润×销售量可得函数解析式;
(2)将所得函数解析式配方成顶点式即可.
解:(1)根据题意可得:w=(x﹣20)y
=(x﹣20)(﹣2x+80)
=﹣2x2+120x﹣1600,
w与x的函数关系式为:w=﹣2x2+120x﹣1600;
(2)根据题意可得:w=﹣2x2+120x﹣1600=﹣2(x﹣30)2+200,
∵﹣2<0,
∴当x=30时,w有最大值.w最大值为200.
答:销售单价定为30元时,每天销售利润最大,最大销售利润200元.
26.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴交于A,B两点,其中B(6,0),与y轴交于点C(0,8),点P是x轴上方的抛物线上一动点(不与点C重合).
(1)求抛物线的表达式;
(2)过点P作PD⊥x轴于点D,交直线BC于点E,点E关于直线PC的对称点为E′,若点E′落在y轴上(不与点C重合),请判断以P,C,E,E′为顶点的四边形的形状,并说明理由;
(3)在(2)的条件下直接写出点P的坐标.
【分析】(1)利用待定系数法求二次函数解析式;
(2)利用对称的性质得∠E′CP=∠ECP,E′C=CE,E′P=EP,由PE∥E′C得∠EPC=∠E′CP,则∠EPC=∠ECP,于是可判断EP=EC,所以EC=EP=PE′=E′C,则根据菱形的判定方法得到四边形EPE′C为菱形;
(3)先利用待定系数法求出直线BC的解析式为y=﹣x+8,根据二次函数和一次函数图象上点的坐标特征,设P(x,﹣x2+x+8),则E(x,﹣x+8),则可计算出PE=﹣x2+x+8﹣(﹣x+8)=﹣x2+4x,过点E作EF⊥y轴于点F,如图,证明△CFE∽△COB,利用相似比可计算出CE=x,则可利用EC=EP得到方程﹣x2+4x=x,然后解方程求出x即可得到P点坐标.
解:(1)把点C(0,8),B(6,0)代入在抛物线y=﹣x2+bx+c得,解得,
所以抛物线的表达式为y=﹣x2+x+8;
(2)以P,C,E,E′为顶点的四边形为菱形.理由如下:
∵E点和E′点关于直线PC对称,
∴∠E′CP=∠ECP,E′C=CE,E′P=EP,
又∵PD⊥x轴,
∴PE∥E′C,
∴∠EPC=∠E′CP,
∴∠EPC=∠ECP,
∴EP=EC,
∴EC=EP=PE′=E′C,
∴四边形EPE′C为菱形,
(3)设直线BC的解析式为y=kx+m,
把B(6,0),C(0,8)代入得,解得,
∴直线BC的解析式为y=﹣x+8;
设P(x,﹣x2+x+8),则E(x,﹣x+8),
∴PE=﹣x2+x+8﹣(﹣x+8)=﹣x2+4x,
过点E作EF⊥y轴于点F,如图,
在Rt△OBC中,BC==10,
∵EF∥OB,
∴△CFE∽△COB,
∴=,即=,
∴CE=x,
∵EC=EP,
∴﹣x2+4x=x,
整理得2x2﹣7x=0,解得x1=0(舍去),x2=,
∴点P的坐标为(,).
同课章节目录
