2019-2020学年黑龙江省哈尔滨南岗区虹桥中学八年级(下)期中数学试卷(五四学制)(Word版 含解析)
文档属性
| 名称 | 2019-2020学年黑龙江省哈尔滨南岗区虹桥中学八年级(下)期中数学试卷(五四学制)(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 06:40:57 | ||
图片预览




文档简介
2019-2020学年黑龙江省哈尔滨南岗区虹桥中学八年级(下)期中数学试卷(五四学制)
一、选择题(每小题3分).
1.下列方程中是一元二次方程的是( )
A.x2=﹣4 B.+x=2
C.x2+y2=5 D.ax2 +bx+c=0
2.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
4.将方程x2+4x+1=0配方后,原方程变形为( )
A.(x+2)2=3 B.(x+4)2=3 C.(x+2)2=﹣3 D.(x+2)2=﹣5
5.顺次连接矩形的四边中点所得的四边形一定是( )
A.菱形 B.矩形 C.平行四边形 D.正方形
6.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C.15 D.2
7.对角线的夹角为60°的矩形,且这个角所对的边长为5cm,则矩形的对角线长是( )
A.5cm B.20cm C.10cm D.10cm
8.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠B=∠C;∠A=∠D
C.AB=CD,CB=AD D.AB=AD,CD=BC
9.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分).
11.在平行四边形ABCD中,∠A与∠B的度数之比为2:3,则∠B的度数是 .
12.已知x=1是方程x2+mx+1=0的一个根,则m= .
13.如果一直角三角形的两条直角边的长分别是3cm和4cm,那么这个直角三角形斜边上的中线等于 cm.
14.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 cm2.
15.三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的解,则此三角形的周长是 .
16.已知关于x的方程x2﹣2x+2k=0有两个不相等实数根,则k的取值范围是 .
17.如图,在矩形纸片ABCD中,AB=6cm,AD=8cm,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则EF= cm.
18.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为 .
19.?ABCD的周长是32cm,∠ABC的平分线交AD所在直线于点E,且AE:ED=3:2,则AB的长为 .
20.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,点E在AB上,∠EDB=∠ADC,点F在BC上,∠AFE=2∠FAC,∠DAF=60°,AF=4,AD=3,则ED= .
三、解答题(21、22各7分,23、24、各8分,25、26、27题各10分,共60分)
21.解下列方程:
(1)x2﹣2x=0;
(2)x2﹣3x﹣4=0.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图1中画出以AB为一边的△ABC,点C在小正方形顶点上,且△ABC的面积为12.
(2)在图2中画出以AB为一腰的等腰直角三角形ABD,点D在小正方形顶点上.
(3)在(2)的条件下,请直接写出AD的长度 .
23.如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
24.如图所示,BD是?ABCD的对角线,AE⊥BD于点E,CF⊥BD于F
(I)求证:四边形AECF是平行四边形;
(2)若E是BF的中点,写出图中所有面积等于△ABE面积2倍的三角形.
25.汽车产业的发展,有效促进了我国现代化建设.某汽车销售公司2016年盈利1000万元,2018年盈利1440万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,预计2019年盈利多少万元?
26.如图1,正方形ABCD沿GF折叠,使B落在CD边上点E处,连接BE,BH.
(1)求∠HBE的度数;
(2)若BH与GF交于点O,连接OE,判断△BOE的形状,说明理由;
(3)在(2)的条件下,作EQ⊥AB于点Q,连接OQ,若AG=2,CE=3,求△OQR的面积.
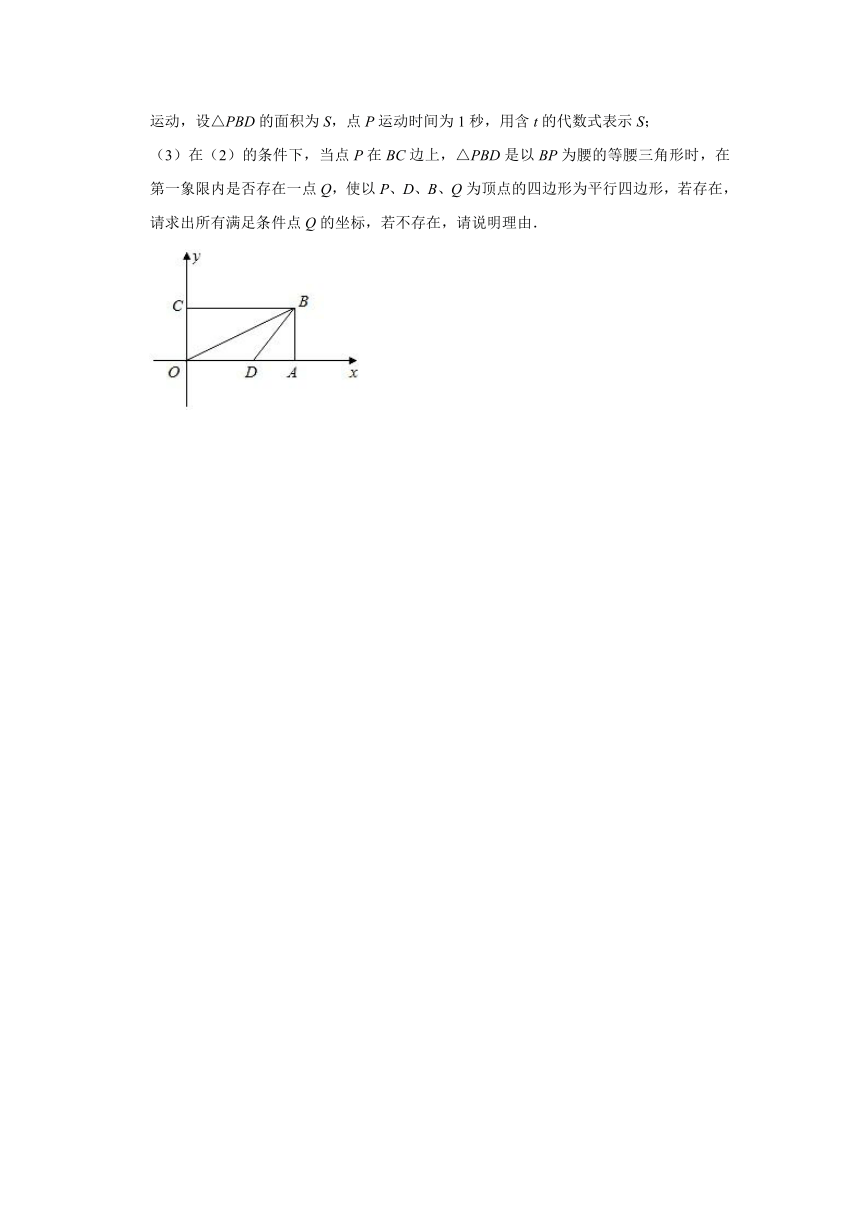
27.如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是矩形,OA边在x轴上,OC边在y轴上,B(8,4),点D在x轴的正半轴上,且∠OBC=∠OBD.
(1)求点D坐标;
(2)动点P从点O出发,沿折线O→B→C方向以2个单位/秒的速度向终点C匀速运动,设△PBD的面积为S,点P运动时间为1秒,用含t的代数式表示S;
(3)在(2)的条件下,当点P在BC边上,△PBD是以BP为腰的等腰三角形时,在第一象限内是否存在一点Q,使以P、D、B、Q为顶点的四边形为平行四边形,若存在,请求出所有满足条件点Q的坐标,若不存在,请说明理由.
参考答案
一、选择题(每小题3分).
1.下列方程中是一元二次方程的是( )
A.x2=﹣4 B.+x=2
C.x2+y2=5 D.ax2 +bx+c=0
解:A、是一元二次方程,故A符合题意;
B、是分式方程,故B不符合题意;
C、是二元二次方程,故C不符合题意;
D、当a=0时不是一元二次方程,故D不符合题意;
故选:A.
2.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
解:A、1.52+22≠32,不符合勾股定理的逆定理,故正确;
B、72+242=252,符合勾股定理的逆定理,故错误;
C、62+82=102,符合勾股定理的逆定理,故错误;
D、92+122=152,符合勾股定理的逆定理,故错误.
故选:A.
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
解:∵四边形ABCD是菱形,
∴AB∥DC,故选项A正确,不合题意;
无法得出AC=BD,故选项B错误,符合题意;
AC⊥BD,故选项C正确,不合题意;
OA=OC,故选项D正确,不合题意;
故选:B.
4.将方程x2+4x+1=0配方后,原方程变形为( )
A.(x+2)2=3 B.(x+4)2=3 C.(x+2)2=﹣3 D.(x+2)2=﹣5
解:∵x2+4x+1=0,
∴x2+4x=﹣1,
∴x2+4x+4=﹣1+4,
∴(x+2)2=3.
故选:A.
5.顺次连接矩形的四边中点所得的四边形一定是( )
A.菱形 B.矩形 C.平行四边形 D.正方形
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:A.
6.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C.15 D.2
解:过P作PE⊥x轴,连接OP,
∵P(﹣2,3),
∴PE=3,OE=2,
∴在Rt△OPE中,根据勾股定理得:OP2=PE2+OE2,
∴OP==,则点P在原点的距离为.
故选:B.
7.对角线的夹角为60°的矩形,且这个角所对的边长为5cm,则矩形的对角线长是( )
A.5cm B.20cm C.10cm D.10cm
解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC,AB=DC=10cm,AC=2AO=2OC,BD=2OB=2OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=5cm,
∴AC=2OA=10cm,
故选:C.
8.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠B=∠C;∠A=∠D
C.AB=CD,CB=AD D.AB=AD,CD=BC
解:A、根据AD∥CD,AD=BC不能判断四边形ABCD是平行四边形,故本选项错误;
B、根据∠B=∠C,∠A=∠D不能判断四边形ABCD是平行四边形,故本选项错误;
C、根据AB=CD,AD=BC,得出四边形ABCD是平行四边形,故本选项正确;
D、根据AB=AD,BC=CD,不能判断四边形ABCD是平行四边形,故本选项错误;
故选:C.
9.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN?AC=AM?MC,
∴MN==.
故选:C.
10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个 B.3个 C.2个 D.1个
解:∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴AE=BF,所以(1)正确;
∴∠ABF=∠EAD,
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,所以(2)正确;
连接BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,所以(3)错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
∴S△AOB=S四边形DEOF,所以(4)正确.
故选:B.
二、填空题(每题3分,共30分)
11.在平行四边形ABCD中,∠A与∠B的度数之比为2:3,则∠B的度数是 108° .
解:∵∠A:∠B=2:3
∴设∠A=2x°,∠B=3x°
∵四边形ABCD是平行四边形
∴∠A+∠B=180°
∴2x+3x=180°
∴x=36°
∴∠B=108°
故答案为:108°
12.已知x=1是方程x2+mx+1=0的一个根,则m= ﹣2 .
解:∵关于x的一元二次方程x2+mx+1=0有一个根是1,
∴12+m+1=0,
解得:m=﹣2,
故答案为:﹣2;
13.如果一直角三角形的两条直角边的长分别是3cm和4cm,那么这个直角三角形斜边上的中线等于 cm.
解:∵两条直角边的长分别是3cm和4cm,
∴斜边==5cm,
∴斜边上的中线=cm.
故答案为:.
14.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 24 cm2.
解:∵一个菱形的两条对角线长分别为6cm和8cm,
∴这个菱形的面积=×6×8=24(cm2).
故答案为:24.
15.三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的解,则此三角形的周长是 13 .
解:x2﹣6x+8=0,
(x﹣2)(x﹣4)=0,
x﹣2=0,x﹣4=0,
x1=2,x2=4,
当x=2时,2+3<6,不符合三角形的三边关系定理,所以x=2舍去,
当x=4时,符合三角形的三边关系定理,三角形的周长是3+6+4=13,
故答案为:13.
16.已知关于x的方程x2﹣2x+2k=0有两个不相等实数根,则k的取值范围是 k< .
解:∵a=1,b=﹣2,c=2k,
∴△=b2﹣4ac=(﹣2)2﹣4×1×2k=4﹣8k>0,
解得:k<.
故答案为:k<.
17.如图,在矩形纸片ABCD中,AB=6cm,AD=8cm,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则EF= 3 cm.
解:∵四边形ABCD是矩形,
∴BC=AD=8cm,∠B=90°
∴AC===10,
∵折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,
∴AF=AB=6,EF=BE,∠AFE=∠B=90°,
∴CF=4,∠CFE=90°,CE=8﹣EF,
∵EF2+CF2=CE2,
∴EF2+42=(8﹣EF)2,
解得:EF=3cm,
故答案为:3.
18.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为 .
解:连接OP,
∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=S矩形ABCD=×6×8=12,
在Rt△BAD中,由勾股定理得:BD===10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴×AO×PE+×DO×PF=12,
∴5PE+5PF=24,
PE+PF=,
故答案为:.
19.?ABCD的周长是32cm,∠ABC的平分线交AD所在直线于点E,且AE:ED=3:2,则AB的长为 6cm或12cm .
解:分两种情况:
①角平分线AD在?ABCD内部,如图1,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴AB+AD=×32=16(cm),∠AEB=∠CBE,
∵∠ABC的平分线交AD所在的直线于点E,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE:ED=3:2,
∴AB:AD=3:5,
∵平行四边形ABCD的周长为32cm.
∴AB的长为:16×=6(cm).
②角平分线AD在?ABCD外部,如图2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴AB+AD=×32=16(cm),∠AEB=∠CBE,
∵∠ABC的平分线交AD所在的直线于点E,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE:ED=3:2,
∴AB:AD=3:1,
∵平行四边形ABCD的周长为32cm.
∴AB的长为:16×=12(cm);
故答案为:6cm或12cm.
20.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,点E在AB上,∠EDB=∠ADC,点F在BC上,∠AFE=2∠FAC,∠DAF=60°,AF=4,AD=3,则ED= 1 .
解:作FM⊥AB于M,延长ED至N使∠DNF=60°,设∠FAC=α,
∵∠BAC=90°,FM⊥AB,
∴MF∥AC,
∴∠MFA=∠FAC=α,
∵∠AFE=2∠FAC=2α,
∴∠MFA=∠MFE=α,
∴∠AEF=∠EAF=90°﹣α,
∴△AEF为等腰三角形,
∴EF=AF=4,
∵∠FDN=∠EDB,∠EDB=∠ADC,
∴∠FDN=∠ADC,
在△DAF和△DNF中,
,
∴△DAF≌△DNF(AAS),
∴NF=AF=4,DN=AD=3,
∵EF=AF=4,
∴EF=NF=4,
∵∠DNF=60°,
∴△ENF是等边三角形,
∴EN=NF=4,
∴ED=EN﹣DN=4﹣3=1.
故答案为:1.
三、解答题(21、22各7分,23、24、各8分,25、26、27题各10分,共60分)
21.解下列方程:
(1)x2﹣2x=0;
(2)x2﹣3x﹣4=0.
解:(1)x(x﹣2)=0,
x=0或x﹣2=0,
所以x1=0,x2=2;
(2)(x﹣4)(x+1)=0,
x﹣4=0或x+1=0,
所以x1=4,x2=﹣1.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图1中画出以AB为一边的△ABC,点C在小正方形顶点上,且△ABC的面积为12.
(2)在图2中画出以AB为一腰的等腰直角三角形ABD,点D在小正方形顶点上.
(3)在(2)的条件下,请直接写出AD的长度 2 .
解:(1)△ABC如图所示.
(2)等腰三角形△ABD如图所示.
(3)AD==2,
故答案为2.
23.如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
解:连接AC,
在△ABC中,
∵∠B=90°,AB=3,BC=4,
∴AC==5,
S△ABC=AB?BC=×3×4=6,
在△ACD中,
∵AD=13,AC=5,CD=12,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴S△ACD=AC?CD=×5×12=30.
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36.
24.如图所示,BD是?ABCD的对角线,AE⊥BD于点E,CF⊥BD于F
(I)求证:四边形AECF是平行四边形;
(2)若E是BF的中点,写出图中所有面积等于△ABE面积2倍的三角形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
(2)解:∵△AEB≌△CFD,
∴BE=DF,
∵E是BF的中点,
∴BE=EF=DF,
∴S△ABF=S△AED=S△BCF=S△ECD=2S△ABE.
∴图中所有面积等于△ABE面积2倍的三角形有:△ABF,△AED,△BFC,△ECD.
25.汽车产业的发展,有效促进了我国现代化建设.某汽车销售公司2016年盈利1000万元,2018年盈利1440万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,预计2019年盈利多少万元?
解:(1)设每年盈利的年增长率为x,
根据题意得1000(1+x)2=1440
解得x1=0.2,x2=﹣2.2(不合题意,舍去)
答:每年盈利的年增长率为20%.
(2)1440(1+0.2)=1728
答:预计2009年该公司盈利1728万元.
26.如图1,正方形ABCD沿GF折叠,使B落在CD边上点E处,连接BE,BH.
(1)求∠HBE的度数;
(2)若BH与GF交于点O,连接OE,判断△BOE的形状,说明理由;
(3)在(2)的条件下,作EQ⊥AB于点Q,连接OQ,若AG=2,CE=3,求△OQR的面积.
解:(1)如图1中,过点E作EN⊥AB于N,过点B作BM⊥EA′于M.
由翻折可知,∠ABF=∠FEA′=90°,FB=FE,
∴∠FBE=∠FEB,
∴∠EBN=∠BEM,
∵∠ENB=∠BME=90°,BE=EB,
∴△ENB≌△BME(AAS),
∴EN=BM,
∵四边形ABCD是正方形,
∴∠NBC=∠C=∠A=∠ENB=90°,AB=BC,
∴AB=BM=BC,
∵BH=BH,BE=BE,
∴Rt△BAH≌Rt△BMH(HL),Rt△BME≌Rt△BCE,
∴∠ABH=∠MBH,∠EBM=∠EBC,
∴∠HBE=∠MBH+∠EBM=∠ABC=45°.
(2)结论:△BOE是等腰直角三角形.
理由:如图2中,
由翻折的旋转可知,FG垂直平分线段BE,
∴OB=EO,
∴∠OBE=∠OEB=45°,
∴OB=OE,∠BOE=90°,
∴△BOE是等腰直角三角形.
(3)如图3中,过点O作OM⊥EQ于M,ON⊥AB于N,过点G作GJ⊥BC于J.
∵∠A=∠ABJ=∠BJG=90°,
∴四边形ABJG是矩形,
∴AG=BJ=2,AB=GJ=BC,
∵FG⊥BE,
∴∠EBC+∠BFG=90°,∠BFG+∠JGF=90°,
∴∠CBE=∠JGF,
∵∠C=∠GJF=90°,BC=GJ,
∴△GJF≌△BCE(AAS),
∴FJ=CE=3,
∴BF=EF=5,CF==4,
∴BC=BF+CF=9,
∴BE===3,
∴OB=OE=3,
∵EQ⊥AB,
∴∠ONB=∠OME=∠OMQ=∠MQN=90°,
∴四边形MQNO是矩形,
∴∠MON=∠BOE=90°,
∴∠BON=∠EOM,
∵OB=OE,
∴△ONB≌△OME(AAS),
∴ON=OM,
∴四边形MQNO是正方形,设OM=OM=NQ=MQ=x,
∵∠C=∠CBQ=∠BQE=90°,
∴四边形BCEQ是矩形,
∴BQ=EC=3,EQ=BC=9,
在Rt△BON中,则有x2+(x+3)2=(3)2,
解得x=3或﹣6(舍弃),
∴OM=QM=3,EM=BN=6,
∵∠BQR=∠OMR=90°,∠BRQ=∠ORM,BQ=OM=3,
∴△BQR≌△OMR(AAS),
∴QR=MR=
∴S△OQR=?QR?OM=××3=.
27.如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是矩形,OA边在x轴上,OC边在y轴上,B(8,4),点D在x轴的正半轴上,且∠OBC=∠OBD.
(1)求点D坐标;
(2)动点P从点O出发,沿折线O→B→C方向以2个单位/秒的速度向终点C匀速运动,设△PBD的面积为S,点P运动时间为1秒,用含t的代数式表示S;
(3)在(2)的条件下,当点P在BC边上,△PBD是以BP为腰的等腰三角形时,在第一象限内是否存在一点Q,使以P、D、B、Q为顶点的四边形为平行四边形,若存在,请求出所有满足条件点Q的坐标,若不存在,请说明理由.
解:(1)∵BC∥AO,
∴∠OBC=∠BOA,
∵∠OBC=∠OBD,
∴∠BOA=∠OBD,
∴BD=OD,
∵B(8,4),即BC=OA=8,AB=CO=4,
∴设BD=OD=x,则有AD=OA﹣OD=8﹣x,
在Rt△ABD中,根据勾股定理得:BD2=AD2+AB2,即x2=(8﹣x)2+42,
解得:x=5,
∴OD=5,即D(5,0);
(2)过D作DE⊥OB于点E,连接PD,如图1所示,
∴∠BED=90°,
在Rt△AOB中,OA=8,AB=4,
根据勾股定理得:OB==4,
∵BD=OD,
∴E为OB的中点,即BE=OB=2,
∵∠CBO=∠DBO,
∴tan∠CBO====tan∠DBO,
∴tan∠DBO==,即DE=,
∵OP=2t,
∴PB=OB﹣OP=4﹣2t,
当0<t≤2时,S△BDP=PB?DE=××(4﹣2t)=﹣5t+10;
过D作DE⊥BC于点E,连接PD,如图2所示,
∵∠DEB=∠EBA=∠BAO=90°,
∴四边形ABED为矩形,
∴DE=AB=4,
∵PB=2t﹣4,
当2<t<2+时,S△BDP=PB?DE=×4×(2t﹣4)=4t﹣8;
综上,S=;
(3)存在,理由:
当PB=BD时,由点B、D的坐标知,BD==3=PB,则点P(3,4),
当PB=PD时,设点P(m,4),则(m﹣8)2=(m﹣5)2+16,解得m=,故点P(,4).
①当点P的坐标为(3,4)时,
(Ⅰ)当PD为边时,
点P向右偏移2个单位向下平移4个单位得到点D,同样,点B(Q)向右偏移2个单位向下平移4个单位得到点Q(B),
则或,解得,
故点Q的坐标为(10,0)(舍去)或(6,8);
(Ⅱ)当PD是对角线时,
由中点公式得:,解得,故点Q的坐标为(0,0)(舍去);
②当点P的坐标为(,4)时,
同理可得,点Q的坐标为(,8);
综上,点Q的坐标为:(6,8)或(,8).
一、选择题(每小题3分).
1.下列方程中是一元二次方程的是( )
A.x2=﹣4 B.+x=2
C.x2+y2=5 D.ax2 +bx+c=0
2.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
4.将方程x2+4x+1=0配方后,原方程变形为( )
A.(x+2)2=3 B.(x+4)2=3 C.(x+2)2=﹣3 D.(x+2)2=﹣5
5.顺次连接矩形的四边中点所得的四边形一定是( )
A.菱形 B.矩形 C.平行四边形 D.正方形
6.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C.15 D.2
7.对角线的夹角为60°的矩形,且这个角所对的边长为5cm,则矩形的对角线长是( )
A.5cm B.20cm C.10cm D.10cm
8.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠B=∠C;∠A=∠D
C.AB=CD,CB=AD D.AB=AD,CD=BC
9.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(每小题3分).
11.在平行四边形ABCD中,∠A与∠B的度数之比为2:3,则∠B的度数是 .
12.已知x=1是方程x2+mx+1=0的一个根,则m= .
13.如果一直角三角形的两条直角边的长分别是3cm和4cm,那么这个直角三角形斜边上的中线等于 cm.
14.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 cm2.
15.三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的解,则此三角形的周长是 .
16.已知关于x的方程x2﹣2x+2k=0有两个不相等实数根,则k的取值范围是 .
17.如图,在矩形纸片ABCD中,AB=6cm,AD=8cm,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则EF= cm.
18.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为 .
19.?ABCD的周长是32cm,∠ABC的平分线交AD所在直线于点E,且AE:ED=3:2,则AB的长为 .
20.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,点E在AB上,∠EDB=∠ADC,点F在BC上,∠AFE=2∠FAC,∠DAF=60°,AF=4,AD=3,则ED= .
三、解答题(21、22各7分,23、24、各8分,25、26、27题各10分,共60分)
21.解下列方程:
(1)x2﹣2x=0;
(2)x2﹣3x﹣4=0.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图1中画出以AB为一边的△ABC,点C在小正方形顶点上,且△ABC的面积为12.
(2)在图2中画出以AB为一腰的等腰直角三角形ABD,点D在小正方形顶点上.
(3)在(2)的条件下,请直接写出AD的长度 .
23.如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
24.如图所示,BD是?ABCD的对角线,AE⊥BD于点E,CF⊥BD于F
(I)求证:四边形AECF是平行四边形;
(2)若E是BF的中点,写出图中所有面积等于△ABE面积2倍的三角形.
25.汽车产业的发展,有效促进了我国现代化建设.某汽车销售公司2016年盈利1000万元,2018年盈利1440万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,预计2019年盈利多少万元?
26.如图1,正方形ABCD沿GF折叠,使B落在CD边上点E处,连接BE,BH.
(1)求∠HBE的度数;
(2)若BH与GF交于点O,连接OE,判断△BOE的形状,说明理由;
(3)在(2)的条件下,作EQ⊥AB于点Q,连接OQ,若AG=2,CE=3,求△OQR的面积.
27.如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是矩形,OA边在x轴上,OC边在y轴上,B(8,4),点D在x轴的正半轴上,且∠OBC=∠OBD.
(1)求点D坐标;
(2)动点P从点O出发,沿折线O→B→C方向以2个单位/秒的速度向终点C匀速运动,设△PBD的面积为S,点P运动时间为1秒,用含t的代数式表示S;
(3)在(2)的条件下,当点P在BC边上,△PBD是以BP为腰的等腰三角形时,在第一象限内是否存在一点Q,使以P、D、B、Q为顶点的四边形为平行四边形,若存在,请求出所有满足条件点Q的坐标,若不存在,请说明理由.
参考答案
一、选择题(每小题3分).
1.下列方程中是一元二次方程的是( )
A.x2=﹣4 B.+x=2
C.x2+y2=5 D.ax2 +bx+c=0
解:A、是一元二次方程,故A符合题意;
B、是分式方程,故B不符合题意;
C、是二元二次方程,故C不符合题意;
D、当a=0时不是一元二次方程,故D不符合题意;
故选:A.
2.下列各组数中不能作为直角三角形的三边长的是( )
A.1.5,2,3 B.7,24,25 C.6,8,10 D.9,12,15
解:A、1.52+22≠32,不符合勾股定理的逆定理,故正确;
B、72+242=252,符合勾股定理的逆定理,故错误;
C、62+82=102,符合勾股定理的逆定理,故错误;
D、92+122=152,符合勾股定理的逆定理,故错误.
故选:A.
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,下列结论中不一定成立的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OC
解:∵四边形ABCD是菱形,
∴AB∥DC,故选项A正确,不合题意;
无法得出AC=BD,故选项B错误,符合题意;
AC⊥BD,故选项C正确,不合题意;
OA=OC,故选项D正确,不合题意;
故选:B.
4.将方程x2+4x+1=0配方后,原方程变形为( )
A.(x+2)2=3 B.(x+4)2=3 C.(x+2)2=﹣3 D.(x+2)2=﹣5
解:∵x2+4x+1=0,
∴x2+4x=﹣1,
∴x2+4x+4=﹣1+4,
∴(x+2)2=3.
故选:A.
5.顺次连接矩形的四边中点所得的四边形一定是( )
A.菱形 B.矩形 C.平行四边形 D.正方形
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=BD,
同理FG=BD,HG=AC,EF=AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:A.
6.在直角坐标系中,点P(﹣2,3)到原点的距离是( )
A. B. C.15 D.2
解:过P作PE⊥x轴,连接OP,
∵P(﹣2,3),
∴PE=3,OE=2,
∴在Rt△OPE中,根据勾股定理得:OP2=PE2+OE2,
∴OP==,则点P在原点的距离为.
故选:B.
7.对角线的夹角为60°的矩形,且这个角所对的边长为5cm,则矩形的对角线长是( )
A.5cm B.20cm C.10cm D.10cm
解:∵四边形ABCD是矩形,
∴∠BAD=90°,AD=BC,AB=DC=10cm,AC=2AO=2OC,BD=2OB=2OD,AC=BD,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OA=OB=AB=5cm,
∴AC=2OA=10cm,
故选:C.
8.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC B.∠B=∠C;∠A=∠D
C.AB=CD,CB=AD D.AB=AD,CD=BC
解:A、根据AD∥CD,AD=BC不能判断四边形ABCD是平行四边形,故本选项错误;
B、根据∠B=∠C,∠A=∠D不能判断四边形ABCD是平行四边形,故本选项错误;
C、根据AB=CD,AD=BC,得出四边形ABCD是平行四边形,故本选项正确;
D、根据AB=AD,BC=CD,不能判断四边形ABCD是平行四边形,故本选项错误;
故选:C.
9.如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A. B. C. D.
解:连接AM,
∵AB=AC,点M为BC中点,
∴AM⊥CM(三线合一),BM=CM,
∵AB=AC=5,BC=6,
∴BM=CM=3,
在Rt△ABM中,AB=5,BM=3,
∴根据勾股定理得:AM===4,
又S△AMC=MN?AC=AM?MC,
∴MN==.
故选:C.
10.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( )
A.4个 B.3个 C.2个 D.1个
解:∵四边形ABCD为正方形,
∴AB=AD=DC,∠BAD=∠D=90°,
而CE=DF,
∴AF=DE,
在△ABF和△DAE中
,
∴△ABF≌△DAE,
∴AE=BF,所以(1)正确;
∴∠ABF=∠EAD,
而∠EAD+∠EAB=90°,
∴∠ABF+∠EAB=90°,
∴∠AOB=90°,
∴AE⊥BF,所以(2)正确;
连接BE,
∵BE>BC,
∴BA≠BE,
而BO⊥AE,
∴OA≠OE,所以(3)错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
∴S△AOB=S四边形DEOF,所以(4)正确.
故选:B.
二、填空题(每题3分,共30分)
11.在平行四边形ABCD中,∠A与∠B的度数之比为2:3,则∠B的度数是 108° .
解:∵∠A:∠B=2:3
∴设∠A=2x°,∠B=3x°
∵四边形ABCD是平行四边形
∴∠A+∠B=180°
∴2x+3x=180°
∴x=36°
∴∠B=108°
故答案为:108°
12.已知x=1是方程x2+mx+1=0的一个根,则m= ﹣2 .
解:∵关于x的一元二次方程x2+mx+1=0有一个根是1,
∴12+m+1=0,
解得:m=﹣2,
故答案为:﹣2;
13.如果一直角三角形的两条直角边的长分别是3cm和4cm,那么这个直角三角形斜边上的中线等于 cm.
解:∵两条直角边的长分别是3cm和4cm,
∴斜边==5cm,
∴斜边上的中线=cm.
故答案为:.
14.已知一个菱形的两条对角线长分别为6cm和8cm,则这个菱形的面积为 24 cm2.
解:∵一个菱形的两条对角线长分别为6cm和8cm,
∴这个菱形的面积=×6×8=24(cm2).
故答案为:24.
15.三角形的两边长分别为3和6,第三边的长是方程x2﹣6x+8=0的解,则此三角形的周长是 13 .
解:x2﹣6x+8=0,
(x﹣2)(x﹣4)=0,
x﹣2=0,x﹣4=0,
x1=2,x2=4,
当x=2时,2+3<6,不符合三角形的三边关系定理,所以x=2舍去,
当x=4时,符合三角形的三边关系定理,三角形的周长是3+6+4=13,
故答案为:13.
16.已知关于x的方程x2﹣2x+2k=0有两个不相等实数根,则k的取值范围是 k< .
解:∵a=1,b=﹣2,c=2k,
∴△=b2﹣4ac=(﹣2)2﹣4×1×2k=4﹣8k>0,
解得:k<.
故答案为:k<.
17.如图,在矩形纸片ABCD中,AB=6cm,AD=8cm,折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,折痕为AE,则EF= 3 cm.
解:∵四边形ABCD是矩形,
∴BC=AD=8cm,∠B=90°
∴AC===10,
∵折叠该纸片,使得AB边落在对角线AC上,点B落在点F处,
∴AF=AB=6,EF=BE,∠AFE=∠B=90°,
∴CF=4,∠CFE=90°,CE=8﹣EF,
∵EF2+CF2=CE2,
∴EF2+42=(8﹣EF)2,
解得:EF=3cm,
故答案为:3.
18.如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为 .
解:连接OP,
∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=S矩形ABCD=×6×8=12,
在Rt△BAD中,由勾股定理得:BD===10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴×AO×PE+×DO×PF=12,
∴5PE+5PF=24,
PE+PF=,
故答案为:.
19.?ABCD的周长是32cm,∠ABC的平分线交AD所在直线于点E,且AE:ED=3:2,则AB的长为 6cm或12cm .
解:分两种情况:
①角平分线AD在?ABCD内部,如图1,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴AB+AD=×32=16(cm),∠AEB=∠CBE,
∵∠ABC的平分线交AD所在的直线于点E,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE:ED=3:2,
∴AB:AD=3:5,
∵平行四边形ABCD的周长为32cm.
∴AB的长为:16×=6(cm).
②角平分线AD在?ABCD外部,如图2,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,AD=BC,
∴AB+AD=×32=16(cm),∠AEB=∠CBE,
∵∠ABC的平分线交AD所在的直线于点E,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE,
∵AE:ED=3:2,
∴AB:AD=3:1,
∵平行四边形ABCD的周长为32cm.
∴AB的长为:16×=12(cm);
故答案为:6cm或12cm.
20.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,点E在AB上,∠EDB=∠ADC,点F在BC上,∠AFE=2∠FAC,∠DAF=60°,AF=4,AD=3,则ED= 1 .
解:作FM⊥AB于M,延长ED至N使∠DNF=60°,设∠FAC=α,
∵∠BAC=90°,FM⊥AB,
∴MF∥AC,
∴∠MFA=∠FAC=α,
∵∠AFE=2∠FAC=2α,
∴∠MFA=∠MFE=α,
∴∠AEF=∠EAF=90°﹣α,
∴△AEF为等腰三角形,
∴EF=AF=4,
∵∠FDN=∠EDB,∠EDB=∠ADC,
∴∠FDN=∠ADC,
在△DAF和△DNF中,
,
∴△DAF≌△DNF(AAS),
∴NF=AF=4,DN=AD=3,
∵EF=AF=4,
∴EF=NF=4,
∵∠DNF=60°,
∴△ENF是等边三角形,
∴EN=NF=4,
∴ED=EN﹣DN=4﹣3=1.
故答案为:1.
三、解答题(21、22各7分,23、24、各8分,25、26、27题各10分,共60分)
21.解下列方程:
(1)x2﹣2x=0;
(2)x2﹣3x﹣4=0.
解:(1)x(x﹣2)=0,
x=0或x﹣2=0,
所以x1=0,x2=2;
(2)(x﹣4)(x+1)=0,
x﹣4=0或x+1=0,
所以x1=4,x2=﹣1.
22.如图所示,在每个小正方形的边长均为1的网格中,线段AB的端点A、B均在小正方形的顶点上.
(1)在图1中画出以AB为一边的△ABC,点C在小正方形顶点上,且△ABC的面积为12.
(2)在图2中画出以AB为一腰的等腰直角三角形ABD,点D在小正方形顶点上.
(3)在(2)的条件下,请直接写出AD的长度 2 .
解:(1)△ABC如图所示.
(2)等腰三角形△ABD如图所示.
(3)AD==2,
故答案为2.
23.如图,在四边形ABCD中,已知AB=3,BC=4,CD=12,AD=13,∠B=90°.求四边形ABCD的面积.
解:连接AC,
在△ABC中,
∵∠B=90°,AB=3,BC=4,
∴AC==5,
S△ABC=AB?BC=×3×4=6,
在△ACD中,
∵AD=13,AC=5,CD=12,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴S△ACD=AC?CD=×5×12=30.
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36.
24.如图所示,BD是?ABCD的对角线,AE⊥BD于点E,CF⊥BD于F
(I)求证:四边形AECF是平行四边形;
(2)若E是BF的中点,写出图中所有面积等于△ABE面积2倍的三角形.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴AE∥CF,∠AEB=∠CFD=90°,
在△AEB和△CFD中,
,
∴△AEB≌△CFD(AAS),
∴AE=CF,
∴四边形AECF是平行四边形.
(2)解:∵△AEB≌△CFD,
∴BE=DF,
∵E是BF的中点,
∴BE=EF=DF,
∴S△ABF=S△AED=S△BCF=S△ECD=2S△ABE.
∴图中所有面积等于△ABE面积2倍的三角形有:△ABF,△AED,△BFC,△ECD.
25.汽车产业的发展,有效促进了我国现代化建设.某汽车销售公司2016年盈利1000万元,2018年盈利1440万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,预计2019年盈利多少万元?
解:(1)设每年盈利的年增长率为x,
根据题意得1000(1+x)2=1440
解得x1=0.2,x2=﹣2.2(不合题意,舍去)
答:每年盈利的年增长率为20%.
(2)1440(1+0.2)=1728
答:预计2009年该公司盈利1728万元.
26.如图1,正方形ABCD沿GF折叠,使B落在CD边上点E处,连接BE,BH.
(1)求∠HBE的度数;
(2)若BH与GF交于点O,连接OE,判断△BOE的形状,说明理由;
(3)在(2)的条件下,作EQ⊥AB于点Q,连接OQ,若AG=2,CE=3,求△OQR的面积.
解:(1)如图1中,过点E作EN⊥AB于N,过点B作BM⊥EA′于M.
由翻折可知,∠ABF=∠FEA′=90°,FB=FE,
∴∠FBE=∠FEB,
∴∠EBN=∠BEM,
∵∠ENB=∠BME=90°,BE=EB,
∴△ENB≌△BME(AAS),
∴EN=BM,
∵四边形ABCD是正方形,
∴∠NBC=∠C=∠A=∠ENB=90°,AB=BC,
∴AB=BM=BC,
∵BH=BH,BE=BE,
∴Rt△BAH≌Rt△BMH(HL),Rt△BME≌Rt△BCE,
∴∠ABH=∠MBH,∠EBM=∠EBC,
∴∠HBE=∠MBH+∠EBM=∠ABC=45°.
(2)结论:△BOE是等腰直角三角形.
理由:如图2中,
由翻折的旋转可知,FG垂直平分线段BE,
∴OB=EO,
∴∠OBE=∠OEB=45°,
∴OB=OE,∠BOE=90°,
∴△BOE是等腰直角三角形.
(3)如图3中,过点O作OM⊥EQ于M,ON⊥AB于N,过点G作GJ⊥BC于J.
∵∠A=∠ABJ=∠BJG=90°,
∴四边形ABJG是矩形,
∴AG=BJ=2,AB=GJ=BC,
∵FG⊥BE,
∴∠EBC+∠BFG=90°,∠BFG+∠JGF=90°,
∴∠CBE=∠JGF,
∵∠C=∠GJF=90°,BC=GJ,
∴△GJF≌△BCE(AAS),
∴FJ=CE=3,
∴BF=EF=5,CF==4,
∴BC=BF+CF=9,
∴BE===3,
∴OB=OE=3,
∵EQ⊥AB,
∴∠ONB=∠OME=∠OMQ=∠MQN=90°,
∴四边形MQNO是矩形,
∴∠MON=∠BOE=90°,
∴∠BON=∠EOM,
∵OB=OE,
∴△ONB≌△OME(AAS),
∴ON=OM,
∴四边形MQNO是正方形,设OM=OM=NQ=MQ=x,
∵∠C=∠CBQ=∠BQE=90°,
∴四边形BCEQ是矩形,
∴BQ=EC=3,EQ=BC=9,
在Rt△BON中,则有x2+(x+3)2=(3)2,
解得x=3或﹣6(舍弃),
∴OM=QM=3,EM=BN=6,
∵∠BQR=∠OMR=90°,∠BRQ=∠ORM,BQ=OM=3,
∴△BQR≌△OMR(AAS),
∴QR=MR=
∴S△OQR=?QR?OM=××3=.
27.如图,在平面直角坐标系中,点O为坐标原点,四边形OABC是矩形,OA边在x轴上,OC边在y轴上,B(8,4),点D在x轴的正半轴上,且∠OBC=∠OBD.
(1)求点D坐标;
(2)动点P从点O出发,沿折线O→B→C方向以2个单位/秒的速度向终点C匀速运动,设△PBD的面积为S,点P运动时间为1秒,用含t的代数式表示S;
(3)在(2)的条件下,当点P在BC边上,△PBD是以BP为腰的等腰三角形时,在第一象限内是否存在一点Q,使以P、D、B、Q为顶点的四边形为平行四边形,若存在,请求出所有满足条件点Q的坐标,若不存在,请说明理由.
解:(1)∵BC∥AO,
∴∠OBC=∠BOA,
∵∠OBC=∠OBD,
∴∠BOA=∠OBD,
∴BD=OD,
∵B(8,4),即BC=OA=8,AB=CO=4,
∴设BD=OD=x,则有AD=OA﹣OD=8﹣x,
在Rt△ABD中,根据勾股定理得:BD2=AD2+AB2,即x2=(8﹣x)2+42,
解得:x=5,
∴OD=5,即D(5,0);
(2)过D作DE⊥OB于点E,连接PD,如图1所示,
∴∠BED=90°,
在Rt△AOB中,OA=8,AB=4,
根据勾股定理得:OB==4,
∵BD=OD,
∴E为OB的中点,即BE=OB=2,
∵∠CBO=∠DBO,
∴tan∠CBO====tan∠DBO,
∴tan∠DBO==,即DE=,
∵OP=2t,
∴PB=OB﹣OP=4﹣2t,
当0<t≤2时,S△BDP=PB?DE=××(4﹣2t)=﹣5t+10;
过D作DE⊥BC于点E,连接PD,如图2所示,
∵∠DEB=∠EBA=∠BAO=90°,
∴四边形ABED为矩形,
∴DE=AB=4,
∵PB=2t﹣4,
当2<t<2+时,S△BDP=PB?DE=×4×(2t﹣4)=4t﹣8;
综上,S=;
(3)存在,理由:
当PB=BD时,由点B、D的坐标知,BD==3=PB,则点P(3,4),
当PB=PD时,设点P(m,4),则(m﹣8)2=(m﹣5)2+16,解得m=,故点P(,4).
①当点P的坐标为(3,4)时,
(Ⅰ)当PD为边时,
点P向右偏移2个单位向下平移4个单位得到点D,同样,点B(Q)向右偏移2个单位向下平移4个单位得到点Q(B),
则或,解得,
故点Q的坐标为(10,0)(舍去)或(6,8);
(Ⅱ)当PD是对角线时,
由中点公式得:,解得,故点Q的坐标为(0,0)(舍去);
②当点P的坐标为(,4)时,
同理可得,点Q的坐标为(,8);
综上,点Q的坐标为:(6,8)或(,8).
同课章节目录
