四川省金阳县北大金阳附属实验学校2020-2021学年七年级下学期半月考试数学试卷(Word版 含答案)
文档属性
| 名称 | 四川省金阳县北大金阳附属实验学校2020-2021学年七年级下学期半月考试数学试卷(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 06:56:23 | ||
图片预览



文档简介
北大金阳附属实验学校下期第一次半月考测试卷
七年级数学
(全卷满分100分,考试时间120分钟)
一、选择题(每小题3分,共39分)
1.如图所示,下列说法中,错误的是(
)
A.∠A与∠EDC是同位角
B.∠A与∠C是同旁内角
C.∠A与∠ADC是同旁内角
D.∠A与∠ABF是内错角
2.如图,AB∥CD,直线EF分别交AB,CD于点E,F,
EG平分∠BEF交CD于点G,若∠EFG=64°,
则∠EGD的大小是(
)
A.132°
B.128°
C.122°
D.112°
如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,
连接CD,CE,若三角形ACD的面积为10,则三角形BCE的面积为(
)
A.5
B.6
C.10
D.4
4.下列命题不正确的是(
)
A.若两个相等的角有一边平行,则另一边也互相平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.经过直线外一点,有且只有一条直线与已知直线平行
5.如图所示,将长方形纸片ABCD折叠,使点D与点B
重合,点C落在点C′处,折痕为EF,若∠ABE=20°,
则∠EFC′的度数为(
)
A.115°
B.120°
C.125°
D.130°
6.
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.
∠1=∠3
B.
∠2+∠4=180°
C.
∠1=∠4
D.
∠3=∠4
7.如图,将三角形直角顶点放在直尺的一边上,若∠1=65°,
则∠2的度数为( )
A.
10°
B.
15°
C.
20°
D.
25°
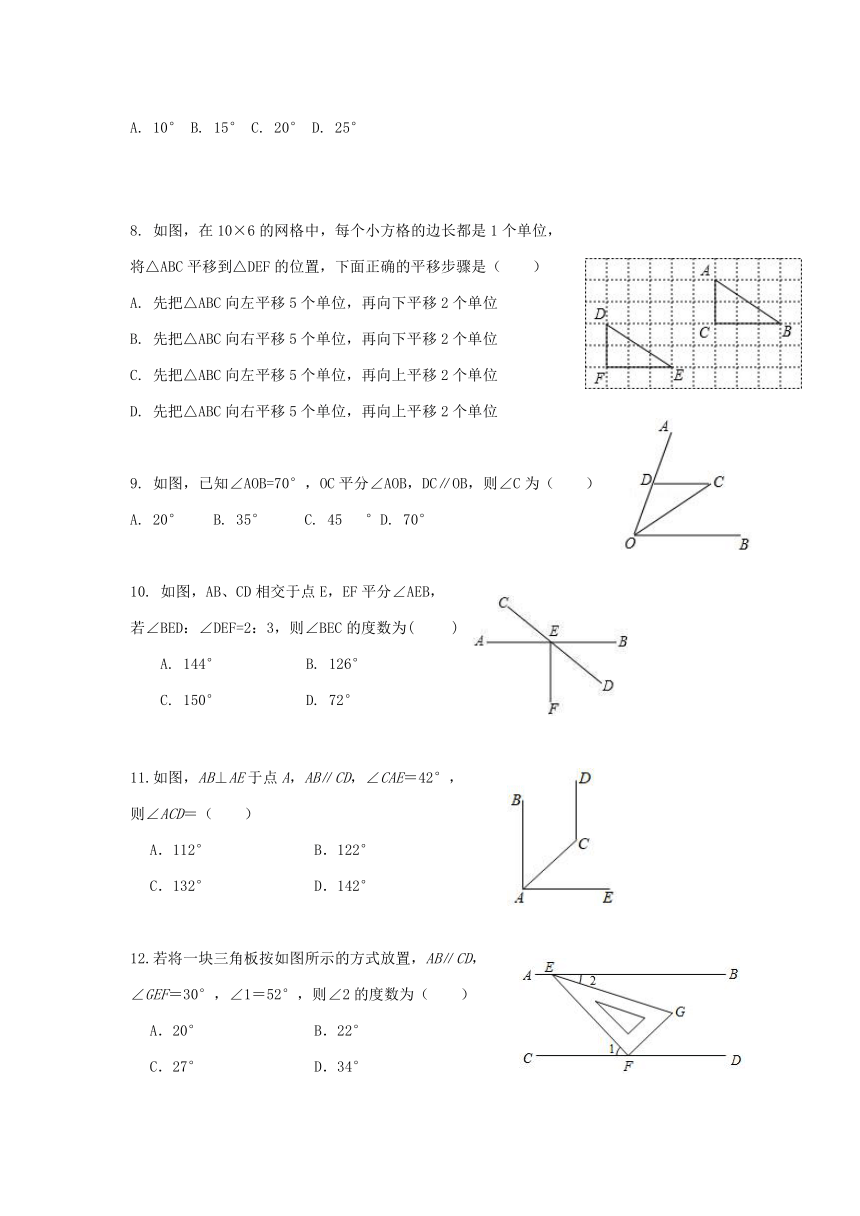
8.
如图,在10×6的网格中,每个小方格的边长都是1个单位,
将△ABC平移到△DEF的位置,下面正确的平移步骤是(
)
A.
先把△ABC向左平移5个单位,再向下平移2个单位
B.
先把△ABC向右平移5个单位,再向下平移2个单位
C.
先把△ABC向左平移5个单位,再向上平移2个单位
D.
先把△ABC向右平移5个单位,再向上平移2个单位
9.
如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A.
20°
B.
35°
C.
45
°D.
70°
如图,AB、CD相交于点E,EF平分∠AEB,
若∠BED:∠DEF=2:3,则∠BEC的度数为(??
)
144°
B.
126°
C.
150°
D.
72°
11.如图,AB⊥AE于点A,AB∥CD,∠CAE=42°,
则∠ACD=( )
A.112°
B.122°
C.132°
D.142°
12.若将一块三角板按如图所示的方式放置,AB∥CD,
∠GEF=30°,∠1=52°,则∠2的度数为( )
A.20°
B.22°
C.27°
D.34°
13.如图,BD为∠ABC的角平分线,AD∥BC,∠BDC=90°,
∠A与∠C的数量关系为( )
A.∠A+∠C=180°
B.∠A-
∠C=90°
C.∠A=2∠C
D.∠A+∠C=90°
二、填空题(每小题3分,共18分)
14.写出一个能说明命题“若|a|>|b|,则a>b”假命题的反例:___________________________________
__________________________________.
15.如图,已知∠1=∠2,∠D=78°,则∠BCD=__________.
16.如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,
则∠BCD的度数为
.
17.如图,AB∥CE,∠ABC=30°,∠BDE=45°,
则∠DBC=
.
18.如图,已知点D,F分别在∠BAC边AB和AC上,
点E在∠BAC的内部,DF平分∠ADE.
若∠BAC=∠BDE=70°,则∠AFD的度数为
.
19.一副三角板按如图所示叠放在一起,其中点
D重合,若固定三角板AOB,改变三角板ACD
的位置(其中A点位置始终不变),
当∠BAD=__________时,CD∥AB.
三、解答题(20、21每小题6分,22小题8分,23小题12分,24小题11分,共43分)
20.如图,四边形ABCD向右平移一段距离后得到
四边形A′B′C′D′.
找出图中存在的平行且相等的四条线段(即四条线段全部互相平行且相等);
(2)找出图中存在的四组相等的角;
(3)四边形ABCD与四边形A′B′C′D′的形状、大小相同吗?为什么?
21.如图是从一个边长为50cm的正方形材料中裁出的一块垫片,现测得BC=DC=50cm,FG=16cm,求这个垫片的周长.
22.如图,已知EF⊥AC,垂足为F,DM⊥AC,垂足为M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试证明AB∥MN.
23.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由.(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:①∠BAD=2∠F;②∠E+∠F=90°.
注:本题第(1)(2)小题在下面解答过程的空格处填写依据或数学式,第(3)小题要写出解题过程.
解:(1)AD∥BC.理由如下:
∵∠ADE+∠ADF=180°(平角的定义),∠ADE+∠BCF=180°(已知),
∴∠ADF=∠__________(____________________),
∴AD∥BC.
(2)AB与EF的位置关系是__________.理由如下:
∵BE平分∠ABC(已知),
∴∠ABE=∠ABC(角平分线的定义).
又∵∠ABC=2∠E(已知),即∠E=∠ABC,
∴∠E=∠__________(____________________).
∴__________∥__________(____________________).
(3)
.
24.如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数(用含α的代数式表示);
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
北大金阳附属实验学校下期第一次半月考
七年级数学参考答案
一、选择题
1-5
BCAAC
6-10
DDABA
11-13
CBC
填空题
14、|-2|>|-1|,但-2<-1(答案不唯一)
15、102°
16、46°
17、15°
18、55°
∠ADC或∠CDA
(填其中一个即可)
20、(1)图中全部互相平行且相等的四条线段是AA′、BB′、CC′、DD′.====
(2)∠BAD=∠B′A′D′,∠ABC=∠A′B′C′,∠BCD=∠B′C′D′,∠CDA=∠C′D′A′(答案不唯一,举出四组即可).
21、50×4+FG+NH=200+32=232(cm).
22、∵EF⊥AC,DM⊥AC,∴∠CFE=∠CMD=90°(垂直的定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠3=∠CDM(两直线平行,同位角相等).
∵∠3=∠2(已知),
∴∠2=∠CDM(等量代换),
∴MN∥CD(内错角相等,两直线平行),
∴∠AMN=∠C(两直线平行,同位角相等).
∵∠1=∠C(已知),
∴∠1=∠AMN(等量代换),
∴AB∥MN(内错角相等,两直线平行).
23、(1)∠BCF
(同角的补角相等)
(2)平行(或AB∥EF)
∠ABE
等量代换
AB
EF
内错角相等,两直线平行
解:
①∵AB∥EF(由(2)知)
∴∠BAF=∠F(两直线平行,内错角相等)
又∵AF平分∠BAD(已知)
∴∠BAD=2∠BAF(角平分线的定义)
∴∠BAD=2∠F(等量代换)
②∵AD∥BC(由(1)知)
∴∠DAB+∠CBA=180°(两直线平行,同旁内角互补)
∵∠OAB=∠DAB(角平分线的定义)
∠OBA=∠CBA(角平分线的定义)
∴∠OAB+∠OBA=(∠DAB+∠CBA)=×180°=90°
由(2)知AB∥EF
∴∠E=∠OBA,∠F=∠OAB(两直线平行,内错角相等)
∴∠E+∠F=∠OBA+∠OAB=90°(等量代换)
24、(1)∵∠AOE+∠AOF=180°,∠AOE=40°(已知)
∴∠AOF=180°-∠AOE=140°(平角的定义)
又∵OC平分∠AOF(已知)
∴∠AOC=∠AOF=×140°=70°(角平分线的定义).
∵OA⊥OB9已知)
∴∠AOB=90°(垂直的定义)
∴∠BOD=180°-∠AOB-∠AOC-=180°-90°-70°=20°.
(2)∵∠AOE+∠AOF=180°,∠AOE=α(已知)
∴∠AOF=180°-∠AOE=180°-α(平角的定义)
又∵OC平分∠AOF(已知)
∴∠AOC=∠AOF=×(180°-α)=90°-α(角平分线的定义).
∵OA⊥OB9已知)
∴∠AOB=90°(垂直的定义)
∴∠BOD=180°-∠AOB-∠AOC-=180°-90°-(90°-α)=α
(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.
七年级数学
(全卷满分100分,考试时间120分钟)
一、选择题(每小题3分,共39分)
1.如图所示,下列说法中,错误的是(
)
A.∠A与∠EDC是同位角
B.∠A与∠C是同旁内角
C.∠A与∠ADC是同旁内角
D.∠A与∠ABF是内错角
2.如图,AB∥CD,直线EF分别交AB,CD于点E,F,
EG平分∠BEF交CD于点G,若∠EFG=64°,
则∠EGD的大小是(
)
A.132°
B.128°
C.122°
D.112°
如图,将三角形ABC沿直线AB向右平移后到达三角形BDE的位置,
连接CD,CE,若三角形ACD的面积为10,则三角形BCE的面积为(
)
A.5
B.6
C.10
D.4
4.下列命题不正确的是(
)
A.若两个相等的角有一边平行,则另一边也互相平行
B.两条直线相交,所成的两组对顶角的平分线互相垂直
C.两条平行线被第三条直线所截,同旁内角的平分线互相垂直
D.经过直线外一点,有且只有一条直线与已知直线平行
5.如图所示,将长方形纸片ABCD折叠,使点D与点B
重合,点C落在点C′处,折痕为EF,若∠ABE=20°,
则∠EFC′的度数为(
)
A.115°
B.120°
C.125°
D.130°
6.
如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
A.
∠1=∠3
B.
∠2+∠4=180°
C.
∠1=∠4
D.
∠3=∠4
7.如图,将三角形直角顶点放在直尺的一边上,若∠1=65°,
则∠2的度数为( )
A.
10°
B.
15°
C.
20°
D.
25°
8.
如图,在10×6的网格中,每个小方格的边长都是1个单位,
将△ABC平移到△DEF的位置,下面正确的平移步骤是(
)
A.
先把△ABC向左平移5个单位,再向下平移2个单位
B.
先把△ABC向右平移5个单位,再向下平移2个单位
C.
先把△ABC向左平移5个单位,再向上平移2个单位
D.
先把△ABC向右平移5个单位,再向上平移2个单位
9.
如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
A.
20°
B.
35°
C.
45
°D.
70°
如图,AB、CD相交于点E,EF平分∠AEB,
若∠BED:∠DEF=2:3,则∠BEC的度数为(??
)
144°
B.
126°
C.
150°
D.
72°
11.如图,AB⊥AE于点A,AB∥CD,∠CAE=42°,
则∠ACD=( )
A.112°
B.122°
C.132°
D.142°
12.若将一块三角板按如图所示的方式放置,AB∥CD,
∠GEF=30°,∠1=52°,则∠2的度数为( )
A.20°
B.22°
C.27°
D.34°
13.如图,BD为∠ABC的角平分线,AD∥BC,∠BDC=90°,
∠A与∠C的数量关系为( )
A.∠A+∠C=180°
B.∠A-
∠C=90°
C.∠A=2∠C
D.∠A+∠C=90°
二、填空题(每小题3分,共18分)
14.写出一个能说明命题“若|a|>|b|,则a>b”假命题的反例:___________________________________
__________________________________.
15.如图,已知∠1=∠2,∠D=78°,则∠BCD=__________.
16.如图,已知AB∥DE,∠ABC=76°,∠CDE=150°,
则∠BCD的度数为
.
17.如图,AB∥CE,∠ABC=30°,∠BDE=45°,
则∠DBC=
.
18.如图,已知点D,F分别在∠BAC边AB和AC上,
点E在∠BAC的内部,DF平分∠ADE.
若∠BAC=∠BDE=70°,则∠AFD的度数为
.
19.一副三角板按如图所示叠放在一起,其中点
D重合,若固定三角板AOB,改变三角板ACD
的位置(其中A点位置始终不变),
当∠BAD=__________时,CD∥AB.
三、解答题(20、21每小题6分,22小题8分,23小题12分,24小题11分,共43分)
20.如图,四边形ABCD向右平移一段距离后得到
四边形A′B′C′D′.
找出图中存在的平行且相等的四条线段(即四条线段全部互相平行且相等);
(2)找出图中存在的四组相等的角;
(3)四边形ABCD与四边形A′B′C′D′的形状、大小相同吗?为什么?
21.如图是从一个边长为50cm的正方形材料中裁出的一块垫片,现测得BC=DC=50cm,FG=16cm,求这个垫片的周长.
22.如图,已知EF⊥AC,垂足为F,DM⊥AC,垂足为M,DM的延长线交AB于点B,且∠1=∠C,点N在AD上,且∠2=∠3,试证明AB∥MN.
23.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由.(2)AB与EF的位置关系如何?为什么?
(3)若AF平分∠BAD,试说明:①∠BAD=2∠F;②∠E+∠F=90°.
注:本题第(1)(2)小题在下面解答过程的空格处填写依据或数学式,第(3)小题要写出解题过程.
解:(1)AD∥BC.理由如下:
∵∠ADE+∠ADF=180°(平角的定义),∠ADE+∠BCF=180°(已知),
∴∠ADF=∠__________(____________________),
∴AD∥BC.
(2)AB与EF的位置关系是__________.理由如下:
∵BE平分∠ABC(已知),
∴∠ABE=∠ABC(角平分线的定义).
又∵∠ABC=2∠E(已知),即∠E=∠ABC,
∴∠E=∠__________(____________________).
∴__________∥__________(____________________).
(3)
.
24.如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数(用含α的代数式表示);
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
北大金阳附属实验学校下期第一次半月考
七年级数学参考答案
一、选择题
1-5
BCAAC
6-10
DDABA
11-13
CBC
填空题
14、|-2|>|-1|,但-2<-1(答案不唯一)
15、102°
16、46°
17、15°
18、55°
∠ADC或∠CDA
(填其中一个即可)
20、(1)图中全部互相平行且相等的四条线段是AA′、BB′、CC′、DD′.====
(2)∠BAD=∠B′A′D′,∠ABC=∠A′B′C′,∠BCD=∠B′C′D′,∠CDA=∠C′D′A′(答案不唯一,举出四组即可).
21、50×4+FG+NH=200+32=232(cm).
22、∵EF⊥AC,DM⊥AC,∴∠CFE=∠CMD=90°(垂直的定义),
∴EF∥DM(同位角相等,两直线平行),
∴∠3=∠CDM(两直线平行,同位角相等).
∵∠3=∠2(已知),
∴∠2=∠CDM(等量代换),
∴MN∥CD(内错角相等,两直线平行),
∴∠AMN=∠C(两直线平行,同位角相等).
∵∠1=∠C(已知),
∴∠1=∠AMN(等量代换),
∴AB∥MN(内错角相等,两直线平行).
23、(1)∠BCF
(同角的补角相等)
(2)平行(或AB∥EF)
∠ABE
等量代换
AB
EF
内错角相等,两直线平行
解:
①∵AB∥EF(由(2)知)
∴∠BAF=∠F(两直线平行,内错角相等)
又∵AF平分∠BAD(已知)
∴∠BAD=2∠BAF(角平分线的定义)
∴∠BAD=2∠F(等量代换)
②∵AD∥BC(由(1)知)
∴∠DAB+∠CBA=180°(两直线平行,同旁内角互补)
∵∠OAB=∠DAB(角平分线的定义)
∠OBA=∠CBA(角平分线的定义)
∴∠OAB+∠OBA=(∠DAB+∠CBA)=×180°=90°
由(2)知AB∥EF
∴∠E=∠OBA,∠F=∠OAB(两直线平行,内错角相等)
∴∠E+∠F=∠OBA+∠OAB=90°(等量代换)
24、(1)∵∠AOE+∠AOF=180°,∠AOE=40°(已知)
∴∠AOF=180°-∠AOE=140°(平角的定义)
又∵OC平分∠AOF(已知)
∴∠AOC=∠AOF=×140°=70°(角平分线的定义).
∵OA⊥OB9已知)
∴∠AOB=90°(垂直的定义)
∴∠BOD=180°-∠AOB-∠AOC-=180°-90°-70°=20°.
(2)∵∠AOE+∠AOF=180°,∠AOE=α(已知)
∴∠AOF=180°-∠AOE=180°-α(平角的定义)
又∵OC平分∠AOF(已知)
∴∠AOC=∠AOF=×(180°-α)=90°-α(角平分线的定义).
∵OA⊥OB9已知)
∴∠AOB=90°(垂直的定义)
∴∠BOD=180°-∠AOB-∠AOC-=180°-90°-(90°-α)=α
(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.
同课章节目录
