2020-2021学年广东省深圳市福田区红岭中学石厦校区九年级(下)开学数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年广东省深圳市福田区红岭中学石厦校区九年级(下)开学数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览



文档简介
2020-2021学年广东省深圳市福田区红岭中学石厦校区九年级(下)开学数学试卷
一.选择题(每小题3分)
1.在﹣2、、0、1这四个数中,最小的数是( )
A.﹣2 B. C.0 D.1
2.《金刚川》上映不久,其票房突破13亿元,1300000000用科学记数法表示为 )
A.1.3×108 B.1.3×109 C.0.13×109 D.13×108
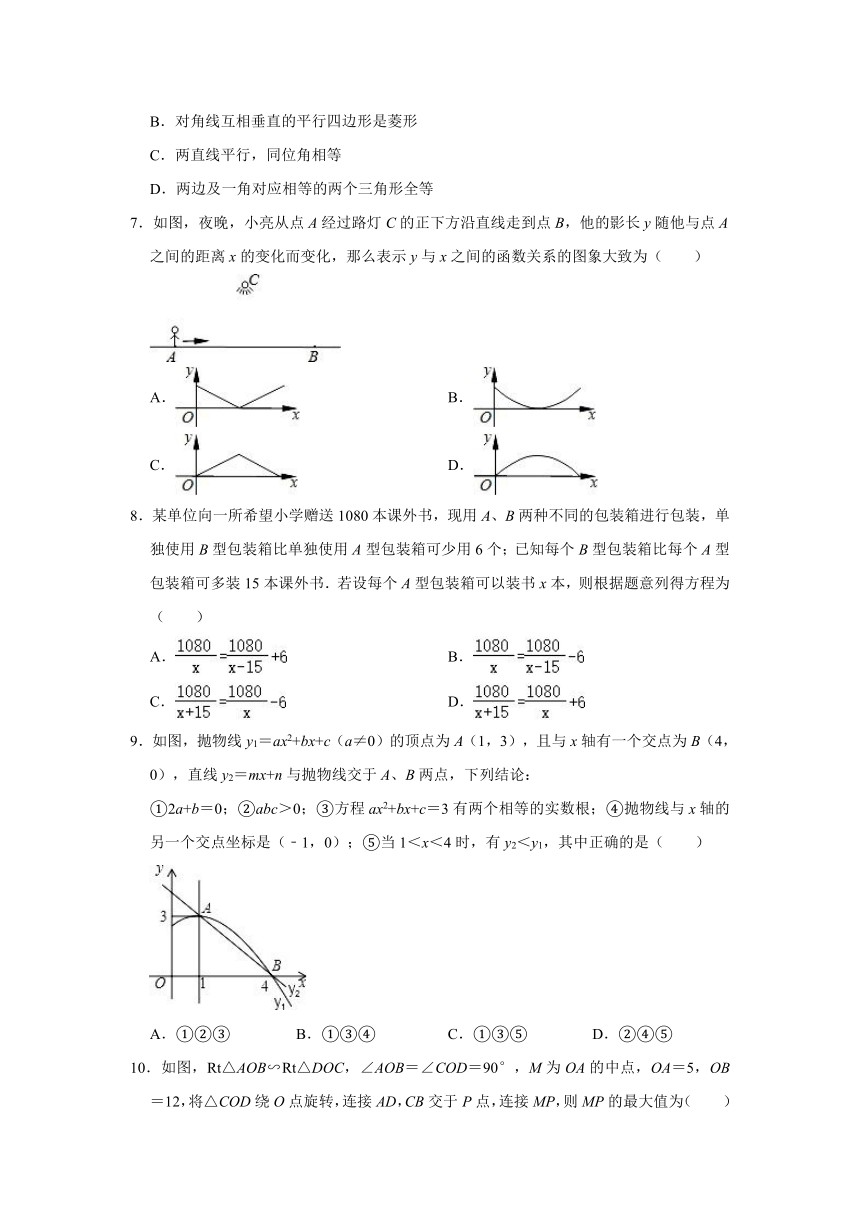
3.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
4.为了调查某小区居民的口罩使用情况,随机抽查了10户家庭的一周使用的口罩数,结果如表,则关于这10户家庭的一周使用的口罩数,下列说法错误的是( )
每周用的口罩数量 20 21 23 30
总数 3 4 2 1
A.中位数是21 B.众数是21 C.极差是10 D.方差是5
5.如图,四边形ABCD内接于圆O,AD∥BC,∠DAB=48°,则∠AOC的度数是( )
A.48° B.96° C.114° D.132°
6.下列说法中,错误的是( )
A.对顶角相等
B.对角线互相垂直的平行四边形是菱形
C.两直线平行,同位角相等
D.两边及一角对应相等的两个三角形全等
7.如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )
A. B.
C. D.
8.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )
A. B.
C. D.
9.如图,抛物线y1=ax2+bx+c(a≠0)的顶点为A(1,3),且与x轴有一个交点为B(4,0),直线y2=mx+n与抛物线交于A、B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点坐标是(﹣1,0);⑤当1<x<4时,有y2<y1,其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
10.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=5,OB=12,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值为( )
A.10 B.11 C.12 D.12.5
二、填空题(每小题3分)
11.因式分解:﹣4a3b3+ab= .
12.某超市今年三月份的营业额为100万元,五月份的营业额为121万元,则四、五两个月每月的平均增长率是 %.
13.如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2= .
14.如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为 .
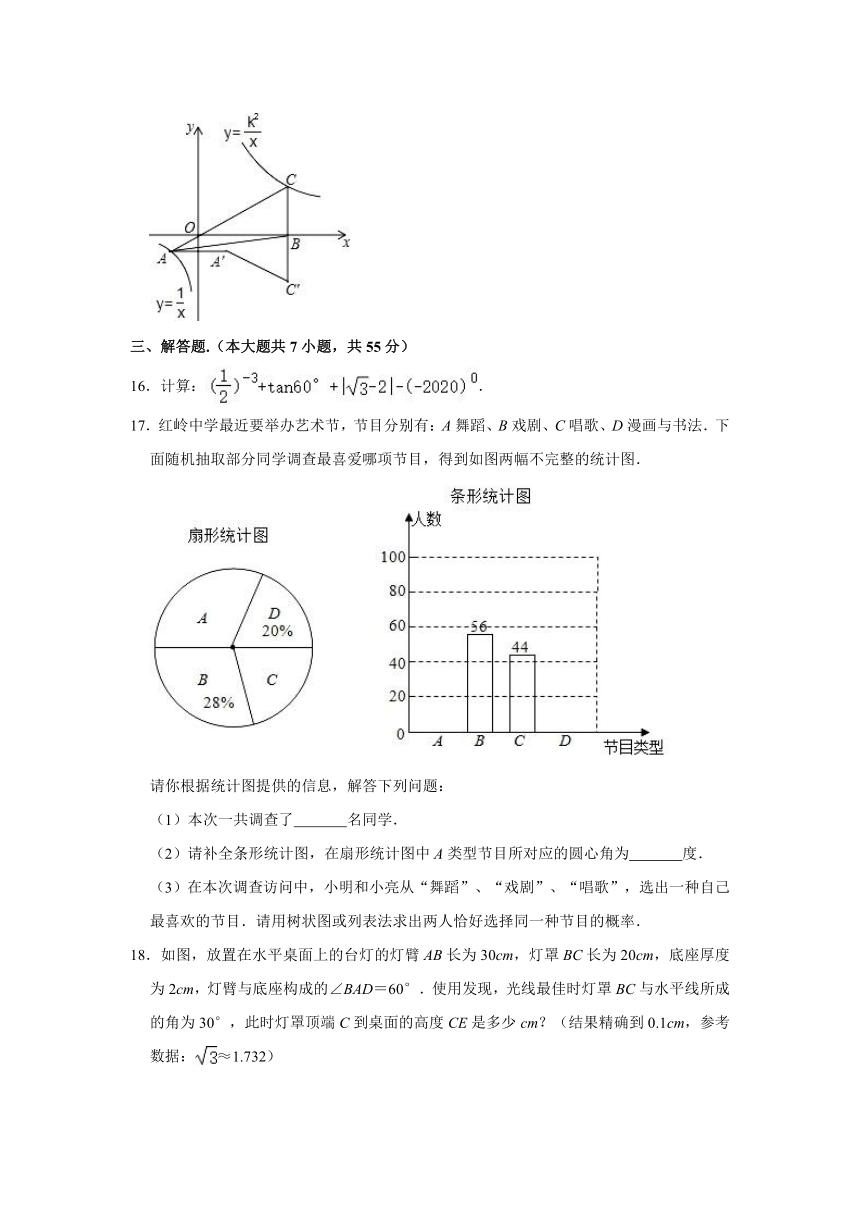
15.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=(x<0)图象上一点,AO的延长线交函数y=(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于 .
三、解答题.(本大题共7小题,共55分)
16.计算:.
17.红岭中学最近要举办艺术节,节目分别有:A舞蹈、B戏剧、C唱歌、D漫画与书法.下面随机抽取部分同学调查最喜爱哪项节目,得到如图两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 名同学.
(2)请补全条形统计图,在扇形统计图中A类型节目所对应的圆心角为 度.
(3)在本次调查访问中,小明和小亮从“舞蹈”、“戏剧”、“唱歌”,选出一种自己最喜欢的节目.请用树状图或列表法求出两人恰好选择同一种节目的概率.
18.如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
19.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
20.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
21.如图,在平面直角坐标系xOy中,直线y=2x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数y=(x>0)交于点C,且BC=2AB,BD∥x轴交反比例函数y=(x>0)于点D,连接AD.
(1)求b,k的值;
(2)求△ABD的面积;
(3)若E为线段BC上一点,过点E作EF∥BD,交反比例函数y=(x>0)于点F,且EF=BD,求点F的坐标.
22.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点C,点D为该二次函数图象顶点.连接BC、AC及CD、BD.
(1)如图1,若点B的坐标(3,0),顶点D坐标(1,4).
①求a的值,并说明∠DBA=∠ACB;
②如图2,点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(2)若a=﹣,点B(1,0),点A(﹣4,0),如图3,动点G在直线AC上方的二次函数图象上.过点G作GE⊥AC于点E,是否存在点G,使得△CGE中的某个角恰好等于∠BAC的2倍?若存在,求出点G的横坐标:若不存在,请说明理由.
参考答案
一.选择题(每小题3分)
1.在﹣2、、0、1这四个数中,最小的数是( )
A.﹣2 B. C.0 D.1
【分析】根据实数大小比较的方法进行比较即可求解.
解:﹣2<﹣<0<1,
最小的数是﹣2.
故选:A.
2.《金刚川》上映不久,其票房突破13亿元,1300000000用科学记数法表示为 )
A.1.3×108 B.1.3×109 C.0.13×109 D.13×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:1300000000=1.3×109.
故选:B.
3.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
【分析】根据从上面看得到的图形事俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.
解:将正方体①移走前的主视图正方形的个数为1,2,1;正方体①移走后的主视图正方形的个数为1,2;主视图发生改变.
将正方体①移走前的左视图正方形的个数为2,1,1;正方体①移走后的左视图正方形的个数为2,1,1;左视图没有发生改变.
将正方体①移走前的俯视图正方形的个数为1,3,1;正方体①移走后的俯视图正方形的个数,1,3;俯视图发生改变.
故选:D.
4.为了调查某小区居民的口罩使用情况,随机抽查了10户家庭的一周使用的口罩数,结果如表,则关于这10户家庭的一周使用的口罩数,下列说法错误的是( )
每周用的口罩数量 20 21 23 30
总数 3 4 2 1
A.中位数是21 B.众数是21 C.极差是10 D.方差是5
【分析】根据中位数的确定方法,将一组数据按大小顺序排列,位于最中间的两个的平均数或最中间一个数据是中位数,众数的定义是在一组数据中出现次数最多的就是众数,极差是一组数据中最大值与最小值的差,运用方差公式求出这组数据的方差.
解:∵这10个数据是:20,20,20,21,21,21,21,23,23,30,
∴中位数是:(21+21)÷2=21吨,故A正确;
∴众数是:21吨,故B正确;
∴极差是:30﹣20=10吨,故C正确;
这组数据的平均数是:(3×20+4×21+2×23+30)÷10=22(吨),
则方差是:×[3×(20﹣22)2+4×(21﹣22)2+2×(23﹣22)2+(30﹣22)2]=8.2,故D错误.
故选:D.
5.如图,四边形ABCD内接于圆O,AD∥BC,∠DAB=48°,则∠AOC的度数是( )
A.48° B.96° C.114° D.132°
【分析】根据平行线的性质求出∠B,根据圆内接四边形的性质求出∠D,根据圆周角定理解答.
解:∵AD∥BC,
∴∠B=180°﹣∠DAB=132°,
∵四边形ABCD内接于圆O,
∴∠D=180°﹣∠B=48°,
由圆周角定理得,∠AOC=2∠D=96°,
故选:B.
6.下列说法中,错误的是( )
A.对顶角相等
B.对角线互相垂直的平行四边形是菱形
C.两直线平行,同位角相等
D.两边及一角对应相等的两个三角形全等
【分析】根据菱形的判定,对顶角的性质,全等三角形的判定可得出答案.
解:A、对顶角相等,本选项说法正确,不符合题意;
B、对角线互相垂直的平行四边形是菱形,本选项说法正确,不符合题意;
C、两直线平行,同位角相等,本选项说法正确,不符合题意;
D、两边及其夹角对应相等的两个三角形全等,本选项说法错误,符合题意;
故选:D.
7.如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )
A. B.
C. D.
【分析】等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
解:设身高GE=h,CF=l,AF=a,
当x≤a时,
在△OEG和△OFC中,
∠GOE=∠COF(公共角),∠AEG=∠AFC=90°,
∴△OEG∽△OFC,
∴=,
∴=,
∴y=x+,
∵a、h、l都是固定的常数,
∴自变量x的系数是固定值,
∴这个函数图象肯定是一次函数图象,即是直线;
∵影长将随着离灯光越来越近而越来越短,到灯下的时候,将是一个点,进而随着离灯光的越来越远而影长将变大.
故选:A.
8.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )
A. B.
C. D.
【分析】关键描述语:单独使用B型包装箱比单独使用A型包装箱可少用6个;可列等量关系为:所用B型包装箱的数量=所用A型包装箱的数量﹣6,由此可得到所求的方程.
解:根据题意,得:.
故选:C.
9.如图,抛物线y1=ax2+bx+c(a≠0)的顶点为A(1,3),且与x轴有一个交点为B(4,0),直线y2=mx+n与抛物线交于A、B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点坐标是(﹣1,0);⑤当1<x<4时,有y2<y1,其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
【分析】根据抛物线对称轴方程对①进行判断;由抛物线开口方向得到a<0,由对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,于是可对②进行判断;根据顶点坐标对③进行判断;根据抛物线的对称性对④进行判断;根据函数图象得当1<x<4时,一次函数图象在抛物线下方,则可对⑤进行判断.
解:∵抛物线的顶点坐标A(1,3)
∴抛物线的对称轴为直线x=﹣=1,
∴2a+b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以②错误;
∵抛物线的顶点坐标A(1,3),
∴x=1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以③正确;
∵抛物线与x轴的一个交点为(4,0)
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(﹣2,0),所以④错误;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(1,3),B点(4,0)
∴当1<x<4时,y2<y1,所以⑤正确.
故选:C.
10.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=5,OB=12,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值为( )
A.10 B.11 C.12 D.12.5
【分析】根据相似三角形的判定定理证明△COB∽△DOA,得到∠OBC=∠OAD,得到O、B、P、A共圆,求出MS和PS,根据三角形三边关系解答即可.
解:取AB的中点S,连接MS、PS,
则PM≤MS+PS,
∵∠AOB=90°,OA=5,OB=12,
∴AB=13,
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∴O、B、P、A共圆,
∴∠APB=∠AOB=90°,
又S是AB的中点,
∴PS=AB=,
∵M为OA的中点,S是AB的中点,
∴MS=OB=6,
∴MP的最大值是6+==12.5,
故选:D.
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解:﹣4a3b3+ab= ab(1+2ab)(1﹣2ab) .
【分析】原式提取公因式,再利用平方差公式分解即可.
解:原式=ab(﹣4a2b2+1)
=ab(1+2ab)(1﹣2ab).
故答案为:ab(1+2ab)(1﹣2ab).
12.某超市今年三月份的营业额为100万元,五月份的营业额为121万元,则四、五两个月每月的平均增长率是 10 %.
【分析】本题可设每月营业额平均增长率为x,则四月份的营业额是100(1+x),五月份的营业额是100(1+x)(1+x),则可以得到方程求解.
解:设四、五两个月每月的平均增长率是x.
根据题意得:100(1+x)2=121,
解得x1=0.1;x2=﹣2.1(不合理舍去).
故四、五两个月每月的平均增长率是10%.
13.如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2= 18 .
【分析】利用相似三角形的性质求出△PAD的面积即可解决问题.
解:∵PA=3PE,PD=3PF,
∴==,
∴EF∥AD,
∴△PEF∽△PAD,
∴=()2,
∵S△PEF=2,
∴S△PAD=18,
∵四边形ABCD是平行四边形,
∴S△PAD=S平行四边形ABCD,
∴S1+S2=S△PAD=18,
故答案为18.
14.如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为 2+ .
【分析】连接OA,过点A作AC⊥OB于点C,由题意知AC=1、OA=OB=2,从而得出OC==、BC=OB﹣OC=2﹣,在Rt△ABC中,根据tan∠ABO=可得答案.
解:如图,连接OA,过点A作AC⊥OB于点C,
则AC=1,OA=OB=2,
∵在Rt△AOC中,OC===,
∴BC=OB﹣OC=2﹣,
∴在Rt△ABC中,tan∠ABO===2+.
故答案是:2+.
15.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=(x<0)图象上一点,AO的延长线交函数y=(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于 10 .
【分析】过A作AD⊥x轴于D,连接OA′,设A(a,),C(b,),由△OAD∽△BCO,得到=()2=,根据反比例函数的系数k的几何意义得到S△ADO=,S△BOC=,求出k2=()2,得到k=﹣,根据S△ABC=S△AOB+S△BOC=(﹣)?b+=6,列出关于k的方程k2+k﹣12=0,求得k=3,由于点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,得到OA′,OC′在同一条直线上,于是得到由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
解:过A作AD⊥x轴于D,连接OA′,
∵点A是函数y=(x<0)图象上一点,
∴设A(a,),
∵点C在函数y=(x>0,k是不等于0的常数)的图象上,
∴设C(b,),
∵AD⊥BD,BC⊥BD,
∴△OAD∽△BCO,
∴=()2=,
∵S△ADO=,S△BOC=,
∴k2=()2,
∵S△ABC=S△AOB+S△BOC=(﹣)?b+=6,
∴k2﹣=12,
①当k>0时,
k=﹣,
∴k2+k﹣12=0,
解得:k=3,k=﹣4(不合题意舍去),
②当k<0时,
k=,
∴k2+k﹣12=0,
解得:k=﹣3,k=4(不合题意舍去),
∴k2=9
∵点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,
∴∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3=90°,
∴OA′,OC′在同一条直线上,
∴S△OBC′=S△OBC==,
∵S△OAA′=2S△OAD=1,
∴由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
故答案为:10.
三、解答题.(本大题共7小题,共55分)
16.计算:.
【分析】分别根据负指数幂的性质、特殊角的三角函数值、绝对值的性质、零指数幂的性质进行化简得出即可.
解:原式=8++2﹣﹣1=9.
17.红岭中学最近要举办艺术节,节目分别有:A舞蹈、B戏剧、C唱歌、D漫画与书法.下面随机抽取部分同学调查最喜爱哪项节目,得到如图两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 200 名同学.
(2)请补全条形统计图,在扇形统计图中A类型节目所对应的圆心角为 108 度.
(3)在本次调查访问中,小明和小亮从“舞蹈”、“戏剧”、“唱歌”,选出一种自己最喜欢的节目.请用树状图或列表法求出两人恰好选择同一种节目的概率.
【分析】(1)由B类人数除以所占百分比即可;
(2)求出D类、A类人数,即可解决问题;
(3)画树状图,再由概率公式求解即可.
解:(1)56÷28%=200(名),
即本次一共调查了200名同学,
故答案为:200;
(2)D类人数为:200×20%=40(名),
则A类人数为200﹣56﹣44﹣40=60(名),
∴360°×=108°,
即在扇形统计图中A类型节目所对应的圆心角为108°,
故答案为:108,
补全条形统计图如下:
(3)把“舞蹈”、“戏剧”、“唱歌”分别记为A、B、C,
画树状图如下:
共有9个等可能的结果,小明和小亮两人恰好选择同一种节目的结果有3个,
∴小明和小亮两人恰好选择同一种节目的概率为=.
18.如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
【分析】首先过点B作BF⊥CD于点F,作BG⊥AD于点G,进而求出FC的长,再求出BG的长,即可得出答案.
解:过点B作BF⊥CD于点F,作BG⊥AD于点G,
∵CE⊥AD,BF⊥CD,BG⊥AD,
∴四边形BFDG矩形,
∴BG=FD
在Rt△BCF中,∠CBF=30°,
∴CF=BC?sin30°=20×=10,
在Rt△ABG中,∠BAG=60°,
∴BG=AB?sin60°=30×=15.
∴CE=CF+FD+DE=10+15+2
=12+15≈37.98≈38.0(cm).
答:此时灯罩顶端C到桌面的高度CE约是38.0cm.
19.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
【分析】(1)先证明四边形ADCE是平行四边形,再证出一组邻边相等,即可得出结论;
(2)过点D作DF⊥CE,垂足为点F;先证明△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.
【解答】(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD=AB=BD=AD,
∴平行四边形ADCE是菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=CDsin60°=6×=3.
20.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
【分析】(1)根据等腰三角形的性质和角平分线的定义证得∠OMB=∠MBF,得出OM∥BF,即可证得OM⊥MF,即可证得结论;
(2)由勾股定理可求AB的长,可得AO,BO,ON的长,由勾股定理可求CO的长,通过证明△ACN∽△MCB,可得,即可求CM的长.
【解答】证明:(1)连接OM,
∵OM=OB,
∴∠OMB=∠OBM,
∵BM平分∠ABD,
∴∠OBM=∠MBF,
∴∠OMB=∠MBF,
∴OM∥BF,
∵MF⊥BD,
∴OM⊥MF,即∠OMF=90°,
∴MF是⊙O的切线;
(2)如图,连接AN,ON
∵=,
∴AN=BN=4
∵AB是直径,=,
∴∠ANB=90°,ON⊥AB
∴AB==4
∴AO=BO=ON=2
∴OC===1
∴AC=2+1,BC=2﹣1
∵∠A=∠NMB,∠ANC=∠MBC
∴△ACN∽△MCB
∴
∴AC?BC=CM?CN
∴7=3?CM
∴CM=
21.如图,在平面直角坐标系xOy中,直线y=2x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数y=(x>0)交于点C,且BC=2AB,BD∥x轴交反比例函数y=(x>0)于点D,连接AD.
(1)求b,k的值;
(2)求△ABD的面积;
(3)若E为线段BC上一点,过点E作EF∥BD,交反比例函数y=(x>0)于点F,且EF=BD,求点F的坐标.
【分析】(1)将点A坐标代入直线解析式中求出b,进而求出点B坐标,再用相似三角形的性质求出CG=2,BG=4,进而求出点C坐标,即可求出k;
(2)先求出点D坐标,进而求出BD,即可得出结论;
(3)先求出EF=3,设出点E坐标,表示出F坐标,利用EF=3建立方程求解即可得出结论.
解:(1)∵直线y=2x+b经过点A(﹣1,0),
∴﹣2+b=0,
∴b=2,
∴直线AB的解析式为y=2x+2,
∴B(0,2),
如图,过点C作CG∥x轴交y轴于G,
∴△AOB∽△CGB,
∴=,
∴CG=2OA=2,BG=2OB=4,
∴OG=OB+BG=6,
∴C(2,6),
∵点C在反比例函数y=的图象上,
∴k=2×6=12;
(2)∵BD∥x轴,且B(0,2),
∴D(6,2),
∴BD=6,
∴S△ABC=BD?OB=6;
(3)由(2)知,BD=6,
∵EF=BD,
∴EF=3,
设E(m,2m+2)(0<m<2),
∴F(,2m+2),
∴EF=﹣m=3,
∴m=﹣2﹣(舍)或m=﹣2+,
∴F(+1,﹣2+2).
22.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点C,点D为该二次函数图象顶点.连接BC、AC及CD、BD.
(1)如图1,若点B的坐标(3,0),顶点D坐标(1,4).
①求a的值,并说明∠DBA=∠ACB;
②如图2,点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(2)若a=﹣,点B(1,0),点A(﹣4,0),如图3,动点G在直线AC上方的二次函数图象上.过点G作GE⊥AC于点E,是否存在点G,使得△CGE中的某个角恰好等于∠BAC的2倍?若存在,求出点G的横坐标:若不存在,请说明理由.
【分析】(1)①根据题意设y=a(x﹣1)2+4,将B(3,0)代入求出a,于是得到结论;求出tan∠OCA=.tan∠DBC=,得出∠DBC=∠OCA,则得出结论;
②先判断出△DEP为等腰三角形.再利用勾股定理建立方程(4﹣h)2=[1﹣(﹣1)]2+h2即可得出结论;
(2)先求出二次函数解析式,进而判断出∠GCE=2∠BAC或∠CGE=2∠BAC,再分两种情况:
①若∠GCE=2∠CAB,判断出y轴是PG的中垂线,即可得出结论;
②若∠EGC=2∠CAB,先求出OH=,再判断出tan∠CGE==,再判断出GM=3k,判断出△AOC∽△MNC,得出MN=2CN,进而得出NG,即可得出结论.
解:(1)①设y=a(x﹣1)2+4,
将B(3,0)代入得,0=a(3﹣1)2+4,
解得a=﹣1.
∴抛物线的解析式是:y=﹣(x﹣1)2+4,
即y=﹣x2+2x+3.
令y=0,则﹣x2+2x+3=0,
∴x1=﹣1,x2=3,
∴A(﹣1,0),
∴OB=OC=3,
∴∠CBO=∠OCB.
∴tan∠OCA=.
∵BC=3,DC=,BD=2,
∴BC2+CD2=BD2,
∴△BCD是直角三角形且∠BCD=90°,
∴tan∠DBC=,
又∵∠DBC和∠OCA都是锐角,
∴∠DBC=∠OCA.
∴∠DBA=∠ACB;
②如图,设直线CD切⊙P于点E.连接PE、PA,作CF⊥DQ于点F.
∴PE⊥CD,PE=PA.
由y=﹣x2+2x+3,得
对称轴为直线x=1,C(0,3)、D(1,4).
∴DF=4﹣3=1,CF=1,
∴DF=CF,
∴△DCF为等腰直角三角形.
∴∠CDF=45°,
∴∠EDP=∠EPD=45°,
∴DE=EP,
∴△DEP为等腰三角形.
设P(1,h),D(1,4).
∴DP=|h﹣4|,
∴EP=|h﹣4|,
∴EP2=(4﹣h)2.
在△APQ中,∠PQA=90°,
∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+h2,
∴(4﹣h)2=[1﹣(﹣1)]2+h2.
整理,得h2+8h﹣8=0,
解得,h=﹣4±2.
∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).
(2)G的横坐标﹣2或﹣.
根据题意得,,
∴,
∴二次函数的解析式为y=﹣x2﹣x+2,
∴C(0,2),
∵A(﹣4.0),
∴OA=4,
∵A(﹣4,0),C(0,2),
∴直线AC的解析式为y=x+2,
在Rt△AOC中,tan∠BAC===<1,
∴∠BAC<45°,
∵GE⊥AC,
∴∠CEG=90°,
∵△CGE中的某个角恰好等于∠BAC的2倍,
∴∠GCE=2∠BAC或∠CGE=2∠BAC,
①若∠GCE=2∠CAB,如图2,过点P作GP∥x轴交直线AC于P,
∴GP⊥y轴,
∴∠GCE=2∠GPC,
∴∠CGP=∠GPC,
∴CG=CP,
∴y轴是PG的中垂线,
设点G的横坐标为m,则点P的横坐标为﹣m,
∴G(m,﹣m2﹣m+2),P(﹣m,﹣m+2),
∴﹣m2﹣m+2=﹣m+2,
∴m1=0,m2=﹣2
∴m=﹣2;
②若∠EGC=2∠CAB,如图3,过点G作GM∥x交AC于M,交y轴于N,
在AO上取一点H,使AH=CH,
则∠CHO=2∠CAB,
根据勾股定理得,(4﹣AH)2+OC2=AH2,
∴AH=,
∴OH=,
∴tan∠CHO==,
∴tan∠CGE=,
在Rt△CEG中,tan∠CGE==,
设CE=4k,GE=3k,则GC=5k,
∵∠GMC=∠CAB,
∴tan∠GMC=tan∠CAB=,
∴,
∴EM=2EG=6k,
∴CM=EM﹣CE=2k,
根据勾股定理得,GM==3k,
∵GM∥x轴,
∴∠CNM=90°,
在Rt△CNM中,CN2+MN2=CM2,
∵GM∥x轴,
∴△AOC∽△MNC,
∴,
∴,
∴MN=2CN,
∴CN2+4CN2=4k2,
∴CN=k,MN=k,
∴NG=GM﹣MN=3k,
设点G的坐标为(n,﹣n2﹣n+2),
∴﹣n=k,﹣n2﹣n+2=2+k,
∴n=﹣或n=0(舍),
即满足条件的点G的横坐标﹣2或﹣.
一.选择题(每小题3分)
1.在﹣2、、0、1这四个数中,最小的数是( )
A.﹣2 B. C.0 D.1
2.《金刚川》上映不久,其票房突破13亿元,1300000000用科学记数法表示为 )
A.1.3×108 B.1.3×109 C.0.13×109 D.13×108
3.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
4.为了调查某小区居民的口罩使用情况,随机抽查了10户家庭的一周使用的口罩数,结果如表,则关于这10户家庭的一周使用的口罩数,下列说法错误的是( )
每周用的口罩数量 20 21 23 30
总数 3 4 2 1
A.中位数是21 B.众数是21 C.极差是10 D.方差是5
5.如图,四边形ABCD内接于圆O,AD∥BC,∠DAB=48°,则∠AOC的度数是( )
A.48° B.96° C.114° D.132°
6.下列说法中,错误的是( )
A.对顶角相等
B.对角线互相垂直的平行四边形是菱形
C.两直线平行,同位角相等
D.两边及一角对应相等的两个三角形全等
7.如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )
A. B.
C. D.
8.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )
A. B.
C. D.
9.如图,抛物线y1=ax2+bx+c(a≠0)的顶点为A(1,3),且与x轴有一个交点为B(4,0),直线y2=mx+n与抛物线交于A、B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点坐标是(﹣1,0);⑤当1<x<4时,有y2<y1,其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
10.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=5,OB=12,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值为( )
A.10 B.11 C.12 D.12.5
二、填空题(每小题3分)
11.因式分解:﹣4a3b3+ab= .
12.某超市今年三月份的营业额为100万元,五月份的营业额为121万元,则四、五两个月每月的平均增长率是 %.
13.如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2= .
14.如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为 .
15.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=(x<0)图象上一点,AO的延长线交函数y=(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于 .
三、解答题.(本大题共7小题,共55分)
16.计算:.
17.红岭中学最近要举办艺术节,节目分别有:A舞蹈、B戏剧、C唱歌、D漫画与书法.下面随机抽取部分同学调查最喜爱哪项节目,得到如图两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 名同学.
(2)请补全条形统计图,在扇形统计图中A类型节目所对应的圆心角为 度.
(3)在本次调查访问中,小明和小亮从“舞蹈”、“戏剧”、“唱歌”,选出一种自己最喜欢的节目.请用树状图或列表法求出两人恰好选择同一种节目的概率.
18.如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
19.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
20.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
21.如图,在平面直角坐标系xOy中,直线y=2x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数y=(x>0)交于点C,且BC=2AB,BD∥x轴交反比例函数y=(x>0)于点D,连接AD.
(1)求b,k的值;
(2)求△ABD的面积;
(3)若E为线段BC上一点,过点E作EF∥BD,交反比例函数y=(x>0)于点F,且EF=BD,求点F的坐标.
22.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点C,点D为该二次函数图象顶点.连接BC、AC及CD、BD.
(1)如图1,若点B的坐标(3,0),顶点D坐标(1,4).
①求a的值,并说明∠DBA=∠ACB;
②如图2,点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(2)若a=﹣,点B(1,0),点A(﹣4,0),如图3,动点G在直线AC上方的二次函数图象上.过点G作GE⊥AC于点E,是否存在点G,使得△CGE中的某个角恰好等于∠BAC的2倍?若存在,求出点G的横坐标:若不存在,请说明理由.
参考答案
一.选择题(每小题3分)
1.在﹣2、、0、1这四个数中,最小的数是( )
A.﹣2 B. C.0 D.1
【分析】根据实数大小比较的方法进行比较即可求解.
解:﹣2<﹣<0<1,
最小的数是﹣2.
故选:A.
2.《金刚川》上映不久,其票房突破13亿元,1300000000用科学记数法表示为 )
A.1.3×108 B.1.3×109 C.0.13×109 D.13×108
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
解:1300000000=1.3×109.
故选:B.
3.如图,是由6个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体( )
A.主视图改变,左视图改变
B.俯视图不变,左视图不变
C.俯视图改变,左视图改变
D.主视图改变,左视图不变
【分析】根据从上面看得到的图形事俯视图,从正面看得到的图形是主视图,从左边看得到的图形是左视图,可得答案.
解:将正方体①移走前的主视图正方形的个数为1,2,1;正方体①移走后的主视图正方形的个数为1,2;主视图发生改变.
将正方体①移走前的左视图正方形的个数为2,1,1;正方体①移走后的左视图正方形的个数为2,1,1;左视图没有发生改变.
将正方体①移走前的俯视图正方形的个数为1,3,1;正方体①移走后的俯视图正方形的个数,1,3;俯视图发生改变.
故选:D.
4.为了调查某小区居民的口罩使用情况,随机抽查了10户家庭的一周使用的口罩数,结果如表,则关于这10户家庭的一周使用的口罩数,下列说法错误的是( )
每周用的口罩数量 20 21 23 30
总数 3 4 2 1
A.中位数是21 B.众数是21 C.极差是10 D.方差是5
【分析】根据中位数的确定方法,将一组数据按大小顺序排列,位于最中间的两个的平均数或最中间一个数据是中位数,众数的定义是在一组数据中出现次数最多的就是众数,极差是一组数据中最大值与最小值的差,运用方差公式求出这组数据的方差.
解:∵这10个数据是:20,20,20,21,21,21,21,23,23,30,
∴中位数是:(21+21)÷2=21吨,故A正确;
∴众数是:21吨,故B正确;
∴极差是:30﹣20=10吨,故C正确;
这组数据的平均数是:(3×20+4×21+2×23+30)÷10=22(吨),
则方差是:×[3×(20﹣22)2+4×(21﹣22)2+2×(23﹣22)2+(30﹣22)2]=8.2,故D错误.
故选:D.
5.如图,四边形ABCD内接于圆O,AD∥BC,∠DAB=48°,则∠AOC的度数是( )
A.48° B.96° C.114° D.132°
【分析】根据平行线的性质求出∠B,根据圆内接四边形的性质求出∠D,根据圆周角定理解答.
解:∵AD∥BC,
∴∠B=180°﹣∠DAB=132°,
∵四边形ABCD内接于圆O,
∴∠D=180°﹣∠B=48°,
由圆周角定理得,∠AOC=2∠D=96°,
故选:B.
6.下列说法中,错误的是( )
A.对顶角相等
B.对角线互相垂直的平行四边形是菱形
C.两直线平行,同位角相等
D.两边及一角对应相等的两个三角形全等
【分析】根据菱形的判定,对顶角的性质,全等三角形的判定可得出答案.
解:A、对顶角相等,本选项说法正确,不符合题意;
B、对角线互相垂直的平行四边形是菱形,本选项说法正确,不符合题意;
C、两直线平行,同位角相等,本选项说法正确,不符合题意;
D、两边及其夹角对应相等的两个三角形全等,本选项说法错误,符合题意;
故选:D.
7.如图,夜晚,小亮从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间的函数关系的图象大致为( )
A. B.
C. D.
【分析】等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
解:设身高GE=h,CF=l,AF=a,
当x≤a时,
在△OEG和△OFC中,
∠GOE=∠COF(公共角),∠AEG=∠AFC=90°,
∴△OEG∽△OFC,
∴=,
∴=,
∴y=x+,
∵a、h、l都是固定的常数,
∴自变量x的系数是固定值,
∴这个函数图象肯定是一次函数图象,即是直线;
∵影长将随着离灯光越来越近而越来越短,到灯下的时候,将是一个点,进而随着离灯光的越来越远而影长将变大.
故选:A.
8.某单位向一所希望小学赠送1080本课外书,现用A、B两种不同的包装箱进行包装,单独使用B型包装箱比单独使用A型包装箱可少用6个;已知每个B型包装箱比每个A型包装箱可多装15本课外书.若设每个A型包装箱可以装书x本,则根据题意列得方程为( )
A. B.
C. D.
【分析】关键描述语:单独使用B型包装箱比单独使用A型包装箱可少用6个;可列等量关系为:所用B型包装箱的数量=所用A型包装箱的数量﹣6,由此可得到所求的方程.
解:根据题意,得:.
故选:C.
9.如图,抛物线y1=ax2+bx+c(a≠0)的顶点为A(1,3),且与x轴有一个交点为B(4,0),直线y2=mx+n与抛物线交于A、B两点,下列结论:
①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点坐标是(﹣1,0);⑤当1<x<4时,有y2<y1,其中正确的是( )
A.①②③ B.①③④ C.①③⑤ D.②④⑤
【分析】根据抛物线对称轴方程对①进行判断;由抛物线开口方向得到a<0,由对称轴位置可得b>0,由抛物线与y轴的交点位置可得c>0,于是可对②进行判断;根据顶点坐标对③进行判断;根据抛物线的对称性对④进行判断;根据函数图象得当1<x<4时,一次函数图象在抛物线下方,则可对⑤进行判断.
解:∵抛物线的顶点坐标A(1,3)
∴抛物线的对称轴为直线x=﹣=1,
∴2a+b=0,所以①正确;
∵抛物线开口向下,
∴a<0,
∴b=﹣2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以②错误;
∵抛物线的顶点坐标A(1,3),
∴x=1时,二次函数有最大值,
∴方程ax2+bx+c=3有两个相等的实数根,所以③正确;
∵抛物线与x轴的一个交点为(4,0)
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(﹣2,0),所以④错误;
∵抛物线y1=ax2+bx+c与直线y2=mx+n(m≠0)交于A(1,3),B点(4,0)
∴当1<x<4时,y2<y1,所以⑤正确.
故选:C.
10.如图,Rt△AOB∽Rt△DOC,∠AOB=∠COD=90°,M为OA的中点,OA=5,OB=12,将△COD绕O点旋转,连接AD,CB交于P点,连接MP,则MP的最大值为( )
A.10 B.11 C.12 D.12.5
【分析】根据相似三角形的判定定理证明△COB∽△DOA,得到∠OBC=∠OAD,得到O、B、P、A共圆,求出MS和PS,根据三角形三边关系解答即可.
解:取AB的中点S,连接MS、PS,
则PM≤MS+PS,
∵∠AOB=90°,OA=5,OB=12,
∴AB=13,
∵∠AOB=∠COD=90°,
∴∠COB=∠DOA,
∵△AOB∽△DOC,
∴,
∴△COB∽△DOA,
∴∠OBC=∠OAD,
∴O、B、P、A共圆,
∴∠APB=∠AOB=90°,
又S是AB的中点,
∴PS=AB=,
∵M为OA的中点,S是AB的中点,
∴MS=OB=6,
∴MP的最大值是6+==12.5,
故选:D.
二、填空题(本大题共5小题,每小题3分,共15分)
11.因式分解:﹣4a3b3+ab= ab(1+2ab)(1﹣2ab) .
【分析】原式提取公因式,再利用平方差公式分解即可.
解:原式=ab(﹣4a2b2+1)
=ab(1+2ab)(1﹣2ab).
故答案为:ab(1+2ab)(1﹣2ab).
12.某超市今年三月份的营业额为100万元,五月份的营业额为121万元,则四、五两个月每月的平均增长率是 10 %.
【分析】本题可设每月营业额平均增长率为x,则四月份的营业额是100(1+x),五月份的营业额是100(1+x)(1+x),则可以得到方程求解.
解:设四、五两个月每月的平均增长率是x.
根据题意得:100(1+x)2=121,
解得x1=0.1;x2=﹣2.1(不合理舍去).
故四、五两个月每月的平均增长率是10%.
13.如图,P为平行四边形ABCD边BC上一点,E、F分别为PA、PD上的点,且PA=3PE,PD=3PF,△PEF、△PDC、△PAB的面积分别记为S、S1、S2.若S=2,则S1+S2= 18 .
【分析】利用相似三角形的性质求出△PAD的面积即可解决问题.
解:∵PA=3PE,PD=3PF,
∴==,
∴EF∥AD,
∴△PEF∽△PAD,
∴=()2,
∵S△PEF=2,
∴S△PAD=18,
∵四边形ABCD是平行四边形,
∴S△PAD=S平行四边形ABCD,
∴S1+S2=S△PAD=18,
故答案为18.
14.如图,在2×2的网格中,以顶点O为圆心,以2个单位长度为半径作圆弧,交图中格线于点A,则tan∠ABO的值为 2+ .
【分析】连接OA,过点A作AC⊥OB于点C,由题意知AC=1、OA=OB=2,从而得出OC==、BC=OB﹣OC=2﹣,在Rt△ABC中,根据tan∠ABO=可得答案.
解:如图,连接OA,过点A作AC⊥OB于点C,
则AC=1,OA=OB=2,
∵在Rt△AOC中,OC===,
∴BC=OB﹣OC=2﹣,
∴在Rt△ABC中,tan∠ABO===2+.
故答案是:2+.
15.如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=(x<0)图象上一点,AO的延长线交函数y=(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于 10 .
【分析】过A作AD⊥x轴于D,连接OA′,设A(a,),C(b,),由△OAD∽△BCO,得到=()2=,根据反比例函数的系数k的几何意义得到S△ADO=,S△BOC=,求出k2=()2,得到k=﹣,根据S△ABC=S△AOB+S△BOC=(﹣)?b+=6,列出关于k的方程k2+k﹣12=0,求得k=3,由于点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,得到OA′,OC′在同一条直线上,于是得到由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
解:过A作AD⊥x轴于D,连接OA′,
∵点A是函数y=(x<0)图象上一点,
∴设A(a,),
∵点C在函数y=(x>0,k是不等于0的常数)的图象上,
∴设C(b,),
∵AD⊥BD,BC⊥BD,
∴△OAD∽△BCO,
∴=()2=,
∵S△ADO=,S△BOC=,
∴k2=()2,
∵S△ABC=S△AOB+S△BOC=(﹣)?b+=6,
∴k2﹣=12,
①当k>0时,
k=﹣,
∴k2+k﹣12=0,
解得:k=3,k=﹣4(不合题意舍去),
②当k<0时,
k=,
∴k2+k﹣12=0,
解得:k=﹣3,k=4(不合题意舍去),
∴k2=9
∵点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,
∴∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3=90°,
∴OA′,OC′在同一条直线上,
∴S△OBC′=S△OBC==,
∵S△OAA′=2S△OAD=1,
∴由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
故答案为:10.
三、解答题.(本大题共7小题,共55分)
16.计算:.
【分析】分别根据负指数幂的性质、特殊角的三角函数值、绝对值的性质、零指数幂的性质进行化简得出即可.
解:原式=8++2﹣﹣1=9.
17.红岭中学最近要举办艺术节,节目分别有:A舞蹈、B戏剧、C唱歌、D漫画与书法.下面随机抽取部分同学调查最喜爱哪项节目,得到如图两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 200 名同学.
(2)请补全条形统计图,在扇形统计图中A类型节目所对应的圆心角为 108 度.
(3)在本次调查访问中,小明和小亮从“舞蹈”、“戏剧”、“唱歌”,选出一种自己最喜欢的节目.请用树状图或列表法求出两人恰好选择同一种节目的概率.
【分析】(1)由B类人数除以所占百分比即可;
(2)求出D类、A类人数,即可解决问题;
(3)画树状图,再由概率公式求解即可.
解:(1)56÷28%=200(名),
即本次一共调查了200名同学,
故答案为:200;
(2)D类人数为:200×20%=40(名),
则A类人数为200﹣56﹣44﹣40=60(名),
∴360°×=108°,
即在扇形统计图中A类型节目所对应的圆心角为108°,
故答案为:108,
补全条形统计图如下:
(3)把“舞蹈”、“戏剧”、“唱歌”分别记为A、B、C,
画树状图如下:
共有9个等可能的结果,小明和小亮两人恰好选择同一种节目的结果有3个,
∴小明和小亮两人恰好选择同一种节目的概率为=.
18.如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据:≈1.732)
【分析】首先过点B作BF⊥CD于点F,作BG⊥AD于点G,进而求出FC的长,再求出BG的长,即可得出答案.
解:过点B作BF⊥CD于点F,作BG⊥AD于点G,
∵CE⊥AD,BF⊥CD,BG⊥AD,
∴四边形BFDG矩形,
∴BG=FD
在Rt△BCF中,∠CBF=30°,
∴CF=BC?sin30°=20×=10,
在Rt△ABG中,∠BAG=60°,
∴BG=AB?sin60°=30×=15.
∴CE=CF+FD+DE=10+15+2
=12+15≈37.98≈38.0(cm).
答:此时灯罩顶端C到桌面的高度CE约是38.0cm.
19.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
【分析】(1)先证明四边形ADCE是平行四边形,再证出一组邻边相等,即可得出结论;
(2)过点D作DF⊥CE,垂足为点F;先证明△BCD是等边三角形,得出∠BDC=∠BCD=60°,CD=BC=6,再由平行线的性质得出∠DCE=∠BDC=60°,在Rt△CDF中,由三角函数求出DF即可.
【解答】(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD=AB=BD=AD,
∴平行四边形ADCE是菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=CDsin60°=6×=3.
20.如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
【分析】(1)根据等腰三角形的性质和角平分线的定义证得∠OMB=∠MBF,得出OM∥BF,即可证得OM⊥MF,即可证得结论;
(2)由勾股定理可求AB的长,可得AO,BO,ON的长,由勾股定理可求CO的长,通过证明△ACN∽△MCB,可得,即可求CM的长.
【解答】证明:(1)连接OM,
∵OM=OB,
∴∠OMB=∠OBM,
∵BM平分∠ABD,
∴∠OBM=∠MBF,
∴∠OMB=∠MBF,
∴OM∥BF,
∵MF⊥BD,
∴OM⊥MF,即∠OMF=90°,
∴MF是⊙O的切线;
(2)如图,连接AN,ON
∵=,
∴AN=BN=4
∵AB是直径,=,
∴∠ANB=90°,ON⊥AB
∴AB==4
∴AO=BO=ON=2
∴OC===1
∴AC=2+1,BC=2﹣1
∵∠A=∠NMB,∠ANC=∠MBC
∴△ACN∽△MCB
∴
∴AC?BC=CM?CN
∴7=3?CM
∴CM=
21.如图,在平面直角坐标系xOy中,直线y=2x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数y=(x>0)交于点C,且BC=2AB,BD∥x轴交反比例函数y=(x>0)于点D,连接AD.
(1)求b,k的值;
(2)求△ABD的面积;
(3)若E为线段BC上一点,过点E作EF∥BD,交反比例函数y=(x>0)于点F,且EF=BD,求点F的坐标.
【分析】(1)将点A坐标代入直线解析式中求出b,进而求出点B坐标,再用相似三角形的性质求出CG=2,BG=4,进而求出点C坐标,即可求出k;
(2)先求出点D坐标,进而求出BD,即可得出结论;
(3)先求出EF=3,设出点E坐标,表示出F坐标,利用EF=3建立方程求解即可得出结论.
解:(1)∵直线y=2x+b经过点A(﹣1,0),
∴﹣2+b=0,
∴b=2,
∴直线AB的解析式为y=2x+2,
∴B(0,2),
如图,过点C作CG∥x轴交y轴于G,
∴△AOB∽△CGB,
∴=,
∴CG=2OA=2,BG=2OB=4,
∴OG=OB+BG=6,
∴C(2,6),
∵点C在反比例函数y=的图象上,
∴k=2×6=12;
(2)∵BD∥x轴,且B(0,2),
∴D(6,2),
∴BD=6,
∴S△ABC=BD?OB=6;
(3)由(2)知,BD=6,
∵EF=BD,
∴EF=3,
设E(m,2m+2)(0<m<2),
∴F(,2m+2),
∴EF=﹣m=3,
∴m=﹣2﹣(舍)或m=﹣2+,
∴F(+1,﹣2+2).
22.如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于A、B两点,交y轴于点C,点D为该二次函数图象顶点.连接BC、AC及CD、BD.
(1)如图1,若点B的坐标(3,0),顶点D坐标(1,4).
①求a的值,并说明∠DBA=∠ACB;
②如图2,点P是抛物线的对称轴上一点,以点P为圆心的圆经过A、B两点,且与直线CD相切,求点P的坐标;
(2)若a=﹣,点B(1,0),点A(﹣4,0),如图3,动点G在直线AC上方的二次函数图象上.过点G作GE⊥AC于点E,是否存在点G,使得△CGE中的某个角恰好等于∠BAC的2倍?若存在,求出点G的横坐标:若不存在,请说明理由.
【分析】(1)①根据题意设y=a(x﹣1)2+4,将B(3,0)代入求出a,于是得到结论;求出tan∠OCA=.tan∠DBC=,得出∠DBC=∠OCA,则得出结论;
②先判断出△DEP为等腰三角形.再利用勾股定理建立方程(4﹣h)2=[1﹣(﹣1)]2+h2即可得出结论;
(2)先求出二次函数解析式,进而判断出∠GCE=2∠BAC或∠CGE=2∠BAC,再分两种情况:
①若∠GCE=2∠CAB,判断出y轴是PG的中垂线,即可得出结论;
②若∠EGC=2∠CAB,先求出OH=,再判断出tan∠CGE==,再判断出GM=3k,判断出△AOC∽△MNC,得出MN=2CN,进而得出NG,即可得出结论.
解:(1)①设y=a(x﹣1)2+4,
将B(3,0)代入得,0=a(3﹣1)2+4,
解得a=﹣1.
∴抛物线的解析式是:y=﹣(x﹣1)2+4,
即y=﹣x2+2x+3.
令y=0,则﹣x2+2x+3=0,
∴x1=﹣1,x2=3,
∴A(﹣1,0),
∴OB=OC=3,
∴∠CBO=∠OCB.
∴tan∠OCA=.
∵BC=3,DC=,BD=2,
∴BC2+CD2=BD2,
∴△BCD是直角三角形且∠BCD=90°,
∴tan∠DBC=,
又∵∠DBC和∠OCA都是锐角,
∴∠DBC=∠OCA.
∴∠DBA=∠ACB;
②如图,设直线CD切⊙P于点E.连接PE、PA,作CF⊥DQ于点F.
∴PE⊥CD,PE=PA.
由y=﹣x2+2x+3,得
对称轴为直线x=1,C(0,3)、D(1,4).
∴DF=4﹣3=1,CF=1,
∴DF=CF,
∴△DCF为等腰直角三角形.
∴∠CDF=45°,
∴∠EDP=∠EPD=45°,
∴DE=EP,
∴△DEP为等腰三角形.
设P(1,h),D(1,4).
∴DP=|h﹣4|,
∴EP=|h﹣4|,
∴EP2=(4﹣h)2.
在△APQ中,∠PQA=90°,
∴AP2=AQ2+PQ2=[1﹣(﹣1)]2+h2,
∴(4﹣h)2=[1﹣(﹣1)]2+h2.
整理,得h2+8h﹣8=0,
解得,h=﹣4±2.
∴点P的坐标为(1,﹣4+2)或(1,﹣4﹣2).
(2)G的横坐标﹣2或﹣.
根据题意得,,
∴,
∴二次函数的解析式为y=﹣x2﹣x+2,
∴C(0,2),
∵A(﹣4.0),
∴OA=4,
∵A(﹣4,0),C(0,2),
∴直线AC的解析式为y=x+2,
在Rt△AOC中,tan∠BAC===<1,
∴∠BAC<45°,
∵GE⊥AC,
∴∠CEG=90°,
∵△CGE中的某个角恰好等于∠BAC的2倍,
∴∠GCE=2∠BAC或∠CGE=2∠BAC,
①若∠GCE=2∠CAB,如图2,过点P作GP∥x轴交直线AC于P,
∴GP⊥y轴,
∴∠GCE=2∠GPC,
∴∠CGP=∠GPC,
∴CG=CP,
∴y轴是PG的中垂线,
设点G的横坐标为m,则点P的横坐标为﹣m,
∴G(m,﹣m2﹣m+2),P(﹣m,﹣m+2),
∴﹣m2﹣m+2=﹣m+2,
∴m1=0,m2=﹣2
∴m=﹣2;
②若∠EGC=2∠CAB,如图3,过点G作GM∥x交AC于M,交y轴于N,
在AO上取一点H,使AH=CH,
则∠CHO=2∠CAB,
根据勾股定理得,(4﹣AH)2+OC2=AH2,
∴AH=,
∴OH=,
∴tan∠CHO==,
∴tan∠CGE=,
在Rt△CEG中,tan∠CGE==,
设CE=4k,GE=3k,则GC=5k,
∵∠GMC=∠CAB,
∴tan∠GMC=tan∠CAB=,
∴,
∴EM=2EG=6k,
∴CM=EM﹣CE=2k,
根据勾股定理得,GM==3k,
∵GM∥x轴,
∴∠CNM=90°,
在Rt△CNM中,CN2+MN2=CM2,
∵GM∥x轴,
∴△AOC∽△MNC,
∴,
∴,
∴MN=2CN,
∴CN2+4CN2=4k2,
∴CN=k,MN=k,
∴NG=GM﹣MN=3k,
设点G的坐标为(n,﹣n2﹣n+2),
∴﹣n=k,﹣n2﹣n+2=2+k,
∴n=﹣或n=0(舍),
即满足条件的点G的横坐标﹣2或﹣.
同课章节目录
