襄阳市优质高中2012届高三年级联考理科数学
文档属性
| 名称 | 襄阳市优质高中2012届高三年级联考理科数学 |

|
|
| 格式 | zip | ||
| 文件大小 | 275.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-04 18:42:04 | ||
图片预览


文档简介
襄阳市优质高中2012届高三年级联考试题
数学(理科)
命题人:陈志华 襄州一中 审题人:李长征 宜城一中;审题人:刘德金 曾都一中
考试时间:2012年1月16日 下午3:00—5:00 试卷满分:150分
注意事项:1.答卷前,考生务必将姓名、准考证号等在答题卡和答题卷上填写清楚
2.选择题答案用2B铅笔直接填涂在答题卡上,非选择题用0.5mm的黑色签字笔在每题对应的答题区域内做答,答在试卷上无效.
第I卷
一、选择题(本大题共10个小题,每小题5分,共50分)
1.若集合则
A. B. C. D.
2.设向量,均为单位向量,且,则与夹角为
A. B. C. D.
3.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=
A.- B.- C. D.
4.如图是花灯展中一款五角星灯连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是
5.已知为虚数单位,为实数,复数在复平面内对应的点为M,则“”是“点M在第二象限”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.若在定义域内均有成立,则称为“和谐函数”.下面为“和谐函数”的是
A. B. C. D.
7.假设神舟八号宇宙飞船以速度(公里/秒)在一轨道上飞行,天宫一号在同一轨道上以速度(公里/秒)与宇宙飞船同向运动.若现在天宫一号在宇宙飞船正前方距离公里处,则太空之吻(即神舟八号与天宫一号交会对接)时间距离现在大约为
A.4秒 B.3秒 C.2秒 D.1秒
8.已知抛物线过焦点F的弦为AB,准线为;将AB绕准线旋转一周得一曲面,则曲面面积最小为(圆柱侧面积公式:;圆台侧面积公式:).
A. B. C. D.
9.在等差数列{}中,若它的前n项和有最小值,且,则
A., B., C., D.,
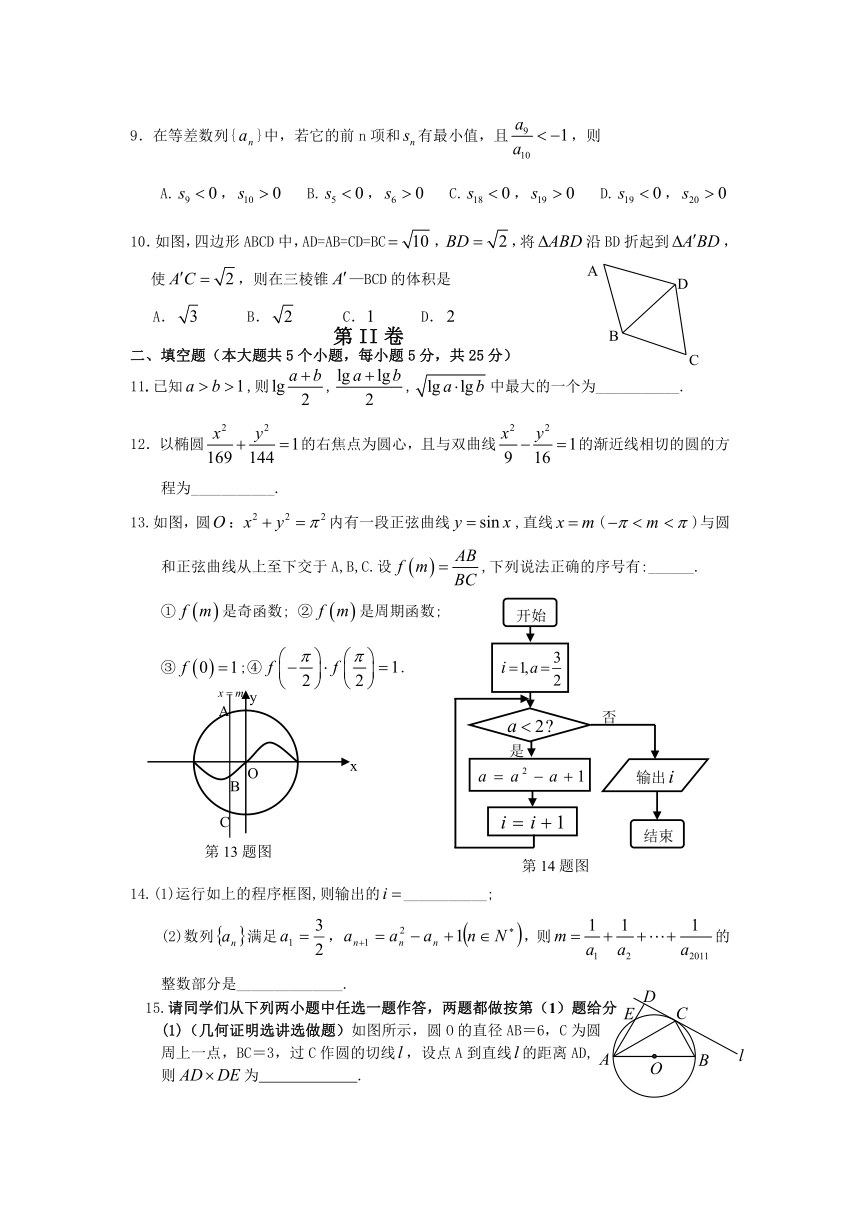
10.如图,四边形ABCD中,AD=AB=CD=BC,,将沿BD折起到,使,则在三棱锥—BCD的体积是
A. B. C. D.
第II卷
二、填空题(本大题共5个小题,每小题5分,共25分)
11.已知,则,,中最大的一个为___________.
12.以椭圆的右焦点为圆心,且与双曲线的渐近线相切的圆的方程为___________.
13.如图,圆:内有一段正弦曲线,直线()与圆和正弦曲线从上至下交于A,B,C.设,下列说法正确的序号有:______.
①是奇函数; ②是周期函数;
③;④.
14.(1)运行如上的程序框图,则输出的___________;
(2)数列满足,,则的整数部分是______________.
15.请同学们从下列两小题中任选一题作答,两题都做按第(1)题给分
(1)(几何证明选讲选做题)如图所示,圆O的直径AB=6,C为圆
周上一点,BC=3,过C作圆的切线,设点A到直线的距离AD,
则为 .
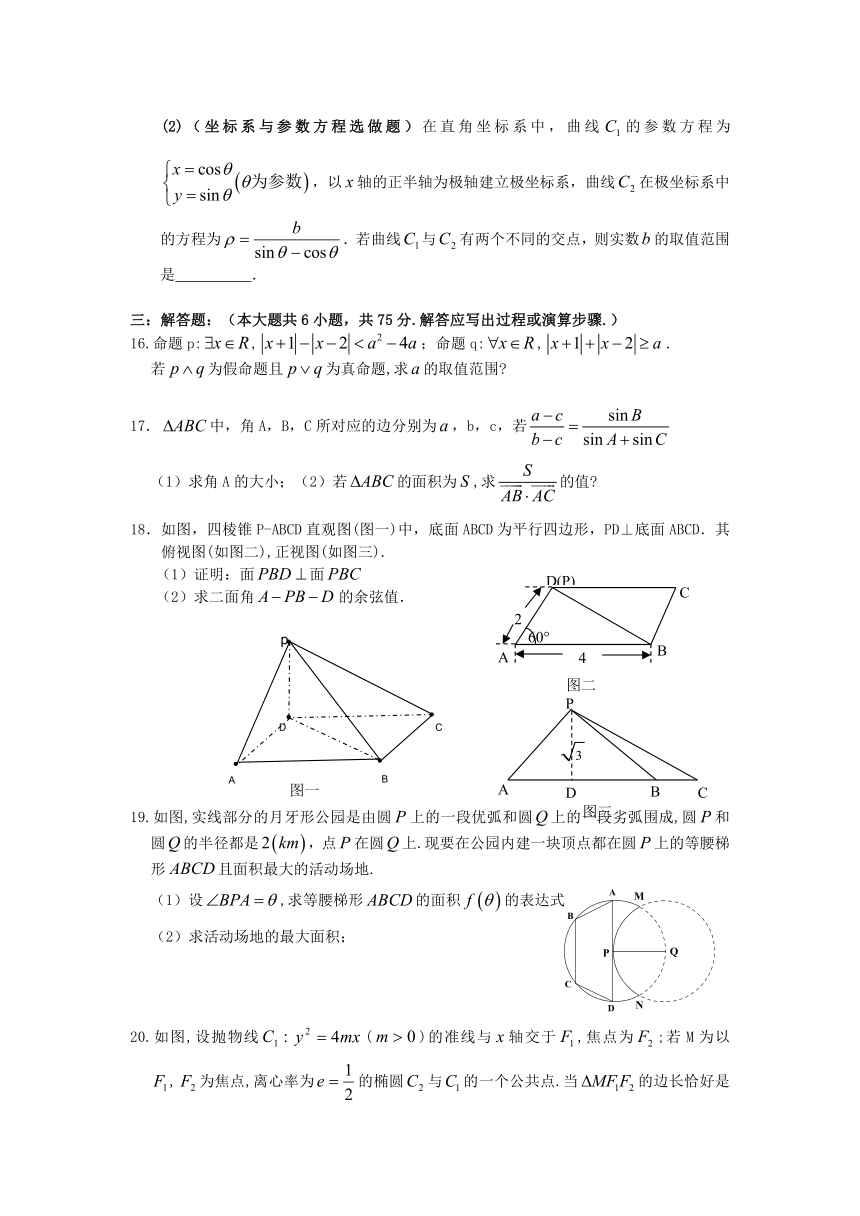
(2)(坐标系与参数方程选做题)在直角坐标系中,曲线的参数方程为,以轴的正半轴为极轴建立极坐标系,曲线在极坐标系中的方程为.若曲线与有两个不同的交点,则实数的取值范围是 .
三:解答题:(本大题共6小题,共75分.解答应写出过程或演算步骤.)
16.命题p:,;命题q:,.
若为假命题且为真命题,求的取值范围
17.中,角A,B,C所对应的边分别为,b,c,若
(1)求角A的大小;(2)若的面积为,求的值
18.如图,四棱锥P-ABCD直观图(图一)中,底面ABCD为平行四边形,PD⊥底面ABCD.其俯视图(如图二),正视图(如图三).
(1)证明:面面
(2)求二面角的余弦值.
19.如图,实线部分的月牙形公园是由圆上的一段优弧和圆上的一段劣弧围成,圆和圆的半径都是,点在圆上.现要在公园内建一块顶点都在圆上的等腰梯形且面积最大的活动场地.
(1)设,求等腰梯形的面积的表达式
(2)求活动场地的最大面积;
20.如图,设抛物线()的准线与轴交于,焦点为;若M为以,为焦点,离心率为的椭圆与的一个公共点.当的边长恰好是三个连续的自然数时.
(1)求椭圆方程
(2)若直线与椭圆交于,两点,当的斜率都存在且都不为0时,求证:的值与无关
21.数列的各项均为正,前项和为,对于,总有,,成等比数列,
(1)求;
(2)若题中增加一个条件,数列能成为等差数列;试探究出增加的条件并写出等差数列的通项公式.
(3)在成为等差数列的条件下,
证明:.
襄阳市优质高中2012届高三年级联考理科数学参考答案
BCBAC BDCCC
7.由选修2-2习题1.7A组第4题改编;
方法一:设交会时间为t则
试根法得
方法二:设交会时间为t则得
9.由Sn有最小值知递增,由且
10.提示:方法一(割)取BD的中点将三棱锥—BCD割成两个三棱锥
方法二(补)以三棱锥—BCD的对棱作长方体对面的对角线补成长方体
11.
12.
13. ③④
14.(1) 则输出的3;……3分
(2)
∴
∴的整数部分为1.……2分
15.(几何证明选讲选做题);(坐标系与参数方程选做题)且
16.解:命题p成立:
(画图象亦可)
有解的条件为,
命题p成立或………4分
命题q成立:命题q成立………8分
为假命题且为真命题一真一假………9分
(没有上面叙述而进行了下面实质讨论,上面一分可以不扣)
P真q假时;………10分;P假q真时.………11分
的取值范围为………12分
17.解: (1)由,得,
即a2=b2+c2-bc,由余弦定理,得:. ………6分
(2)且
………12分
18.(本小题满分12分)
(本小题主要考查空间线线、线面关系,二面角,三视图等知识,考查化归与转化数学思想方法,及空间想象能力、推理论证能力、运算求解能力.由2011年宁夏高考题第18题改编)
解:(1)证明:在三角形ABD中,因为,
所以,
……6分
(2)建立如图的坐标系,设点的坐标分别是
则,
设平面PAB的法向量为,所以, 得
令得,由平面PDB的法向量为,
于是,,因此二面角的余弦值是.……12分
19.解:(1)要求场地面积的最大值,只需考虑切圆于时的情形.
设,则有
…… (6分)(无范围扣1分)
(2)令则
若又时,时,,函数在处取得极大值也是最大值,(无单调性扣1分)
故时,场地面积取得最大值为(km2). ……… (12分)
20. 【解析】(1)由题意又
可得椭圆方程……… (2分)
联立得
或(舍去) ……… (4分)
(也可由)
得,,
当的边长恰好是三个连续的自然数时,.
所以椭圆方程……… (7分)
(2)方法一:由(1)知设
得则
且
……… (13分)
方法二:设,则
相减得
同理
21.【解析】(1),,成等比数列,
当时
数列隔项成等差数列且公差为2
取得
………4分
(2)要使数列能成为等差数列必须
增加的条件可以为(答案不唯一等均可)
………8分
(3)先证
方法一:数学归纳法,
i) 时,左边右边命题成立;
ii)假设时命题成立,即
时左边
又
时成立
综合i) ii)得成立………11分
方法二:柯西不等式
………11分
再证
方法一:数学归纳法,
i)时,左边右边命题成立;
ii)假设时命题成立,即
时左边
设
令则
递减
时成立;
综合i) ii)得成立………14分
方法二:设
递减
令得
方法三: 设如图,将图中小矩形面积分别记为
则不足近似曲边梯形面积
D
C
B
A
y
A
C
O
B
EMBED Equation.DSMT4
x
否
是
输出
结束
开始
第13题图
第14题图
A
B
C
D(P)
图二
图一
D
B
C
A
p
图三
P
A
D
B
C
M
O
x
y
A
C
B
D
A
p
x
C
y
z
B
D
1
2
3
n-1
n
x
y
0
数学(理科)
命题人:陈志华 襄州一中 审题人:李长征 宜城一中;审题人:刘德金 曾都一中
考试时间:2012年1月16日 下午3:00—5:00 试卷满分:150分
注意事项:1.答卷前,考生务必将姓名、准考证号等在答题卡和答题卷上填写清楚
2.选择题答案用2B铅笔直接填涂在答题卡上,非选择题用0.5mm的黑色签字笔在每题对应的答题区域内做答,答在试卷上无效.
第I卷
一、选择题(本大题共10个小题,每小题5分,共50分)
1.若集合则
A. B. C. D.
2.设向量,均为单位向量,且,则与夹角为
A. B. C. D.
3.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=
A.- B.- C. D.
4.如图是花灯展中一款五角星灯连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是
5.已知为虚数单位,为实数,复数在复平面内对应的点为M,则“”是“点M在第二象限”的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
6.若在定义域内均有成立,则称为“和谐函数”.下面为“和谐函数”的是
A. B. C. D.
7.假设神舟八号宇宙飞船以速度(公里/秒)在一轨道上飞行,天宫一号在同一轨道上以速度(公里/秒)与宇宙飞船同向运动.若现在天宫一号在宇宙飞船正前方距离公里处,则太空之吻(即神舟八号与天宫一号交会对接)时间距离现在大约为
A.4秒 B.3秒 C.2秒 D.1秒
8.已知抛物线过焦点F的弦为AB,准线为;将AB绕准线旋转一周得一曲面,则曲面面积最小为(圆柱侧面积公式:;圆台侧面积公式:).
A. B. C. D.
9.在等差数列{}中,若它的前n项和有最小值,且,则
A., B., C., D.,
10.如图,四边形ABCD中,AD=AB=CD=BC,,将沿BD折起到,使,则在三棱锥—BCD的体积是
A. B. C. D.
第II卷
二、填空题(本大题共5个小题,每小题5分,共25分)
11.已知,则,,中最大的一个为___________.
12.以椭圆的右焦点为圆心,且与双曲线的渐近线相切的圆的方程为___________.
13.如图,圆:内有一段正弦曲线,直线()与圆和正弦曲线从上至下交于A,B,C.设,下列说法正确的序号有:______.
①是奇函数; ②是周期函数;
③;④.
14.(1)运行如上的程序框图,则输出的___________;
(2)数列满足,,则的整数部分是______________.
15.请同学们从下列两小题中任选一题作答,两题都做按第(1)题给分
(1)(几何证明选讲选做题)如图所示,圆O的直径AB=6,C为圆
周上一点,BC=3,过C作圆的切线,设点A到直线的距离AD,
则为 .
(2)(坐标系与参数方程选做题)在直角坐标系中,曲线的参数方程为,以轴的正半轴为极轴建立极坐标系,曲线在极坐标系中的方程为.若曲线与有两个不同的交点,则实数的取值范围是 .
三:解答题:(本大题共6小题,共75分.解答应写出过程或演算步骤.)
16.命题p:,;命题q:,.
若为假命题且为真命题,求的取值范围
17.中,角A,B,C所对应的边分别为,b,c,若
(1)求角A的大小;(2)若的面积为,求的值
18.如图,四棱锥P-ABCD直观图(图一)中,底面ABCD为平行四边形,PD⊥底面ABCD.其俯视图(如图二),正视图(如图三).
(1)证明:面面
(2)求二面角的余弦值.
19.如图,实线部分的月牙形公园是由圆上的一段优弧和圆上的一段劣弧围成,圆和圆的半径都是,点在圆上.现要在公园内建一块顶点都在圆上的等腰梯形且面积最大的活动场地.
(1)设,求等腰梯形的面积的表达式
(2)求活动场地的最大面积;
20.如图,设抛物线()的准线与轴交于,焦点为;若M为以,为焦点,离心率为的椭圆与的一个公共点.当的边长恰好是三个连续的自然数时.
(1)求椭圆方程
(2)若直线与椭圆交于,两点,当的斜率都存在且都不为0时,求证:的值与无关
21.数列的各项均为正,前项和为,对于,总有,,成等比数列,
(1)求;
(2)若题中增加一个条件,数列能成为等差数列;试探究出增加的条件并写出等差数列的通项公式.
(3)在成为等差数列的条件下,
证明:.
襄阳市优质高中2012届高三年级联考理科数学参考答案
BCBAC BDCCC
7.由选修2-2习题1.7A组第4题改编;
方法一:设交会时间为t则
试根法得
方法二:设交会时间为t则得
9.由Sn有最小值知递增,由且
10.提示:方法一(割)取BD的中点将三棱锥—BCD割成两个三棱锥
方法二(补)以三棱锥—BCD的对棱作长方体对面的对角线补成长方体
11.
12.
13. ③④
14.(1) 则输出的3;……3分
(2)
∴
∴的整数部分为1.……2分
15.(几何证明选讲选做题);(坐标系与参数方程选做题)且
16.解:命题p成立:
(画图象亦可)
有解的条件为,
命题p成立或………4分
命题q成立:命题q成立………8分
为假命题且为真命题一真一假………9分
(没有上面叙述而进行了下面实质讨论,上面一分可以不扣)
P真q假时;………10分;P假q真时.………11分
的取值范围为………12分
17.解: (1)由,得,
即a2=b2+c2-bc,由余弦定理,得:. ………6分
(2)且
………12分
18.(本小题满分12分)
(本小题主要考查空间线线、线面关系,二面角,三视图等知识,考查化归与转化数学思想方法,及空间想象能力、推理论证能力、运算求解能力.由2011年宁夏高考题第18题改编)
解:(1)证明:在三角形ABD中,因为,
所以,
……6分
(2)建立如图的坐标系,设点的坐标分别是
则,
设平面PAB的法向量为,所以, 得
令得,由平面PDB的法向量为,
于是,,因此二面角的余弦值是.……12分
19.解:(1)要求场地面积的最大值,只需考虑切圆于时的情形.
设,则有
…… (6分)(无范围扣1分)
(2)令则
若又时,时,,函数在处取得极大值也是最大值,(无单调性扣1分)
故时,场地面积取得最大值为(km2). ……… (12分)
20. 【解析】(1)由题意又
可得椭圆方程……… (2分)
联立得
或(舍去) ……… (4分)
(也可由)
得,,
当的边长恰好是三个连续的自然数时,.
所以椭圆方程……… (7分)
(2)方法一:由(1)知设
得则
且
……… (13分)
方法二:设,则
相减得
同理
21.【解析】(1),,成等比数列,
当时
数列隔项成等差数列且公差为2
取得
………4分
(2)要使数列能成为等差数列必须
增加的条件可以为(答案不唯一等均可)
………8分
(3)先证
方法一:数学归纳法,
i) 时,左边右边命题成立;
ii)假设时命题成立,即
时左边
又
时成立
综合i) ii)得成立………11分
方法二:柯西不等式
………11分
再证
方法一:数学归纳法,
i)时,左边右边命题成立;
ii)假设时命题成立,即
时左边
设
令则
递减
时成立;
综合i) ii)得成立………14分
方法二:设
递减
令得
方法三: 设如图,将图中小矩形面积分别记为
则不足近似曲边梯形面积
D
C
B
A
y
A
C
O
B
EMBED Equation.DSMT4
x
否
是
输出
结束
开始
第13题图
第14题图
A
B
C
D(P)
图二
图一
D
B
C
A
p
图三
P
A
D
B
C
M
O
x
y
A
C
B
D
A
p
x
C
y
z
B
D
1
2
3
n-1
n
x
y
0
同课章节目录
