19.2.2.3一次函数解析式的确定 同步练习(含答案)
文档属性
| 名称 | 19.2.2.3一次函数解析式的确定 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
19.2.2.3一次函数解析式的确定同步练习
一、单选题
1.能表示如图所示的一次函数图象的解析式是( )
A. B. C. D.
2.已知某一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数为( )
A.y=﹣x﹣2 B.y=﹣x+10 C.y=﹣x﹣6 D.y=﹣x﹣10
3.已知一次函数的图象过点(0,3),且与两坐标轴围成的三角形的面积为3,则这个一次函数的表达式为( )
A.y=1.5x+3 B.y=-1.5x+3
C.y=1.5x+3或y=-1.5x+3 D.y=1.5x-3或y=-1.5x-3
4.若一次函数y=kx+b的图象与直线y=﹣x+1平行,且过点(8,2),则此一次函数的解析式为( )
A.y=﹣x﹣2 B.y=﹣x﹣6 C.y=﹣x﹣1 D.y=﹣x+10
5.已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为 ( )
A.y= x+2 B.y= ﹣x+2 C.y= x+2或y=﹣x+2 D.y= - x+2或y = x-2
6.已知一次函数()的图像与两坐标轴所围成的三角形的面积等于,则该一次函数表达式为( )
A. B. C. D.
7.已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则k的值为( )
A.3 B.-3 C.3或-3 D.不确定
8.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为10,则该直线的函数表达式是( )
A.y=x+5 B.y=x+10 C.y=-x+5 D.y=-x+10
9.直线y=2x﹣6关于y轴对称的直线的解析式为( )
A.y=2x+6 B.y=﹣2x+6 C.y=﹣2x﹣6 D.y=2x﹣6
10.直线y=x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(-3,0) B.(-6,0) C.(-,0) D.(-,0)
二、填空题
11.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
12.含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为______.
13.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb=__.
15.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是___.
16.已知与成正比例关系,且当时,,则时, _______.
三、解答题
17.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=S△BOC,求点D的坐标.
18.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
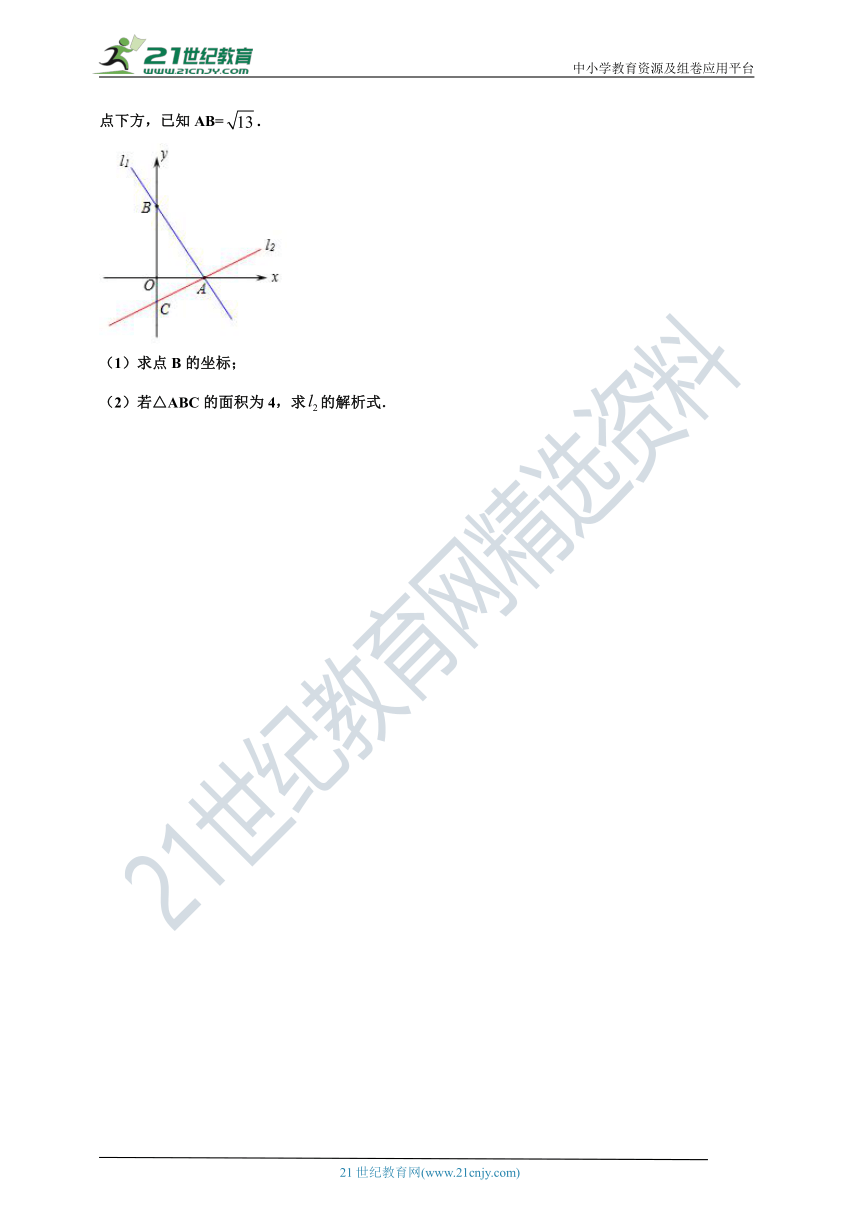
19.如图,过点A(2,0)的两条直线,分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=.
(1)求点B的坐标;
(2)若△ABC的面积为4,求的解析式.
答案
一、单选题
1.A 2.B 3.C 4.D 5.C 6.B 7.C 8.C 9.C 10.C
二、填空题
11.y=2x+10
12.
13.-8
14.或或等.
15..
16.2
三、解答题
17.详解:(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:,
解得:.
(2)当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m)(m<0),
∵S△COD=S△BOC,即﹣m=××4×3,
解得:m=-4,
∴点D的坐标为(0,-4).
18.【详解】(1)把C(m,4)代入一次函数y=﹣x+5,可得
4=﹣m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣;
故k的值为或2或﹣.
19.【详解】
(1)在Rt△AOB中,
∵,
∴,
∴OB=3,
∴点B的坐标是(0,3) .
(2)∵=BC?OA,
∴BC×2=4,
∴BC=4,
∴C(0,-1).
设的解析式为,
把A(2,0),C(0,-1)代入得:,
∴,
∴的解析式为是.
20.试题解析:
(1)∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),
∴2m=2,
m=1.
把(1,2)和(-2,-1)代入y=kx+b,得
解得:
则一次函数解析式是y=x+1;
(2)令x=0,则y=1,即点C(0,1);
(3)令y=0,则x=-1.
则△AOD的面积=.
_21?????????è?????(www.21cnjy.com)_
19.2.2.3一次函数解析式的确定同步练习
一、单选题
1.能表示如图所示的一次函数图象的解析式是( )
A. B. C. D.
2.已知某一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数为( )
A.y=﹣x﹣2 B.y=﹣x+10 C.y=﹣x﹣6 D.y=﹣x﹣10
3.已知一次函数的图象过点(0,3),且与两坐标轴围成的三角形的面积为3,则这个一次函数的表达式为( )
A.y=1.5x+3 B.y=-1.5x+3
C.y=1.5x+3或y=-1.5x+3 D.y=1.5x-3或y=-1.5x-3
4.若一次函数y=kx+b的图象与直线y=﹣x+1平行,且过点(8,2),则此一次函数的解析式为( )
A.y=﹣x﹣2 B.y=﹣x﹣6 C.y=﹣x﹣1 D.y=﹣x+10
5.已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,则一次函数的解析式为 ( )
A.y= x+2 B.y= ﹣x+2 C.y= x+2或y=﹣x+2 D.y= - x+2或y = x-2
6.已知一次函数()的图像与两坐标轴所围成的三角形的面积等于,则该一次函数表达式为( )
A. B. C. D.
7.已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则k的值为( )
A.3 B.-3 C.3或-3 D.不确定
8.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为10,则该直线的函数表达式是( )
A.y=x+5 B.y=x+10 C.y=-x+5 D.y=-x+10
9.直线y=2x﹣6关于y轴对称的直线的解析式为( )
A.y=2x+6 B.y=﹣2x+6 C.y=﹣2x﹣6 D.y=2x﹣6
10.直线y=x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(-3,0) B.(-6,0) C.(-,0) D.(-,0)
二、填空题
11.一次函数y=kx+b与y=2x+1平行,且经过点(﹣3,4),则表达式为:_____.
12.含45°角的直角三角板如图放置在平面直角坐标系中,其中A(-2,0),B(0,1),则直线BC的解析式为______.
13.如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb=__.
15.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是___.
16.已知与成正比例关系,且当时,,则时, _______.
三、解答题
17.如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=S△BOC,求点D的坐标.
18.如图,直角坐标系xOy中,一次函数y=﹣x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
(1)求m的值及l2的解析式;
(2)求S△AOC﹣S△BOC的值;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,直接写出k的值.
19.如图,过点A(2,0)的两条直线,分别交y轴于B,C,其中点B在原点上方,点C在原点下方,已知AB=.
(1)求点B的坐标;
(2)若△ABC的面积为4,求的解析式.
答案
一、单选题
1.A 2.B 3.C 4.D 5.C 6.B 7.C 8.C 9.C 10.C
二、填空题
11.y=2x+10
12.
13.-8
14.或或等.
15..
16.2
三、解答题
17.详解:(1)当x=1时,y=3x=3,
∴点C的坐标为(1,3).
将A(﹣2,6)、C(1,3)代入y=kx+b,
得:,
解得:.
(2)当y=0时,有﹣x+4=0,
解得:x=4,
∴点B的坐标为(4,0).
设点D的坐标为(0,m)(m<0),
∵S△COD=S△BOC,即﹣m=××4×3,
解得:m=-4,
∴点D的坐标为(0,-4).
18.【详解】(1)把C(m,4)代入一次函数y=﹣x+5,可得
4=﹣m+5,
解得m=2,
∴C(2,4),
设l2的解析式为y=ax,则4=2a,
解得a=2,
∴l2的解析式为y=2x;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=4,CE=2,
y=﹣x+5,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC﹣S△BOC=×10×4﹣×5×2=20﹣5=15;
(3)一次函数y=kx+1的图象为l3,且11,l2,l3不能围成三角形,
∴当l3经过点C(2,4)时,k=;
当l2,l3平行时,k=2;
当11,l3平行时,k=﹣;
故k的值为或2或﹣.
19.【详解】
(1)在Rt△AOB中,
∵,
∴,
∴OB=3,
∴点B的坐标是(0,3) .
(2)∵=BC?OA,
∴BC×2=4,
∴BC=4,
∴C(0,-1).
设的解析式为,
把A(2,0),C(0,-1)代入得:,
∴,
∴的解析式为是.
20.试题解析:
(1)∵正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),
∴2m=2,
m=1.
把(1,2)和(-2,-1)代入y=kx+b,得
解得:
则一次函数解析式是y=x+1;
(2)令x=0,则y=1,即点C(0,1);
(3)令y=0,则x=-1.
则△AOD的面积=.
_21?????????è?????(www.21cnjy.com)_
