19.1.1.1变量 同步练习(含答案)
图片预览


文档简介
中小学教育资源及组卷应用平台
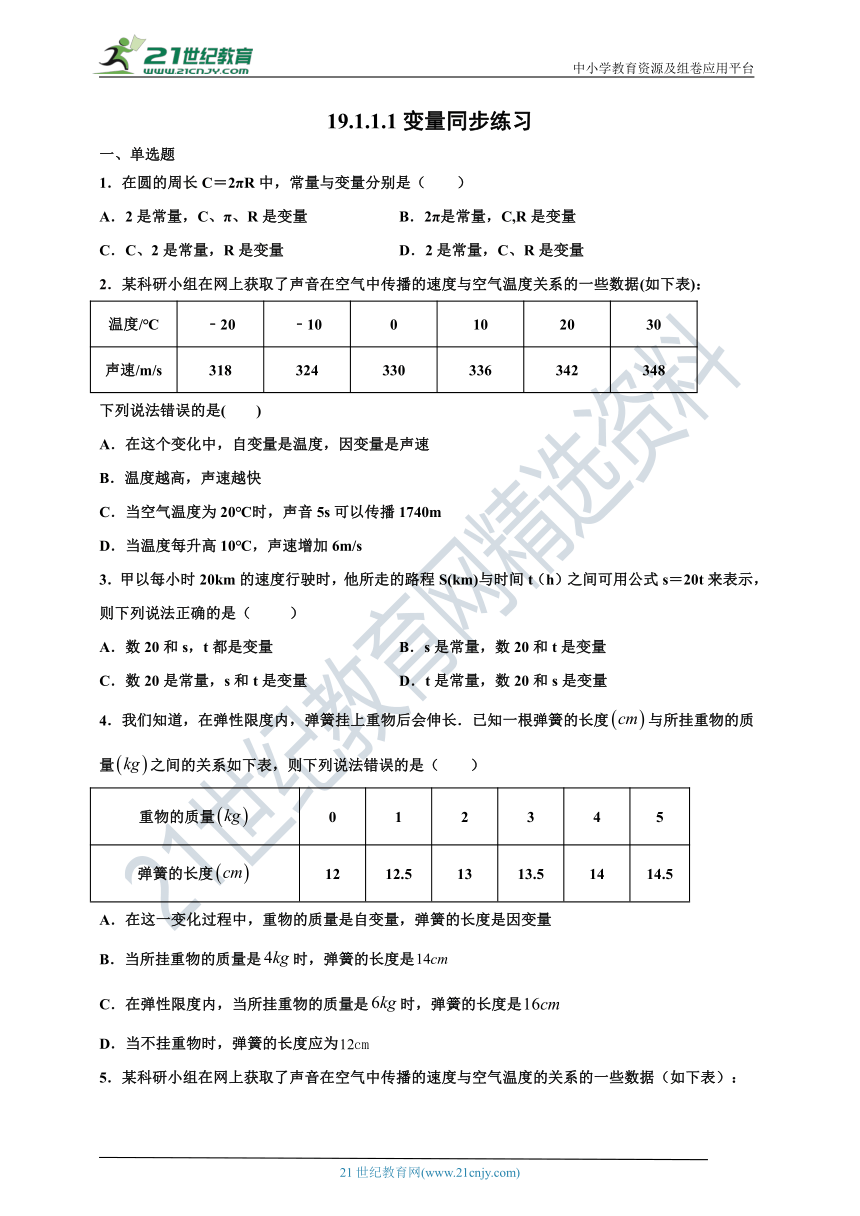
19.1.1.1变量同步练习
一、单选题
1.在圆的周长C=2πR中,常量与变量分别是( )
A.2是常量,C、π、R是变量 B.2π是常量,C,R是变量
C.C、2是常量,R是变量 D.2是常量,C、R是变量
2.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
3.甲以每小时20km的速度行驶时,他所走的路程S(km)与时间t(h)之间可用公式s=20t来表示,则下列说法正确的是( )
A.数20和s,t都是变量 B.s是常量,数20和t是变量
C.数20是常量,s和t是变量 D.t是常量,数20和s是变量
4.我们知道,在弹性限度内,弹簧挂上重物后会伸长.已知一根弹簧的长度与所挂重物的质量之间的关系如下表,则下列说法错误的是( )?
重物的质量 0 1 2 3 4 5
弹簧的长度 12 12.5 13 13.5 14 14.5
A.在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量
B.当所挂重物的质量是时,弹簧的长度是
C.在弹性限度内,当所挂重物的质量是时,弹簧的长度是
D.当不挂重物时,弹簧的长度应为
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度的关系的一些数据(如下表):
气温
声速
下列说法正确的是( )
A.在这个变化中,自变量是声速,因变量是气温
B.温度越高,声速越慢
C.当气温为时,声音可以传播
D.气温每升高,声速减小
6.某商城进一批苹果,在6月27日按照早中晚三个批次销售,销售情况如表,在该变化过程中,常量是( )
A.批次 B.销售量 C.收入 D.单价
7.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
8.设路程为s(km),速度为v(km/h),时间为t(h),当s=60时,v=,在这个函数关系式中( )
A.s是常量,t是s的函数
B.v是常量,t是v的函数
C.t是常量,v是t的函数
D.s是常量,t是自变量,v是t的函数
二、填空题
9.果字成熟后从树上落到地面,它落下的高度与经过的时间有如下的关系:
时间(秒) 0.5 0.6 0.7 0.8 0.9 1
落下的高度(米)
如果果子经过2秒落到地上,那么此果子开始落下时离地面的高度大约是__________米.
10.圆的面积与半径之间的关系是,请指出公式中常量是 ______________________.
11.某烤鸡店在确定烤鸡的烤制时间时,主要依据的是下面表格的数据:
鸡的质量(kg) 0.5 1 1.5 2 2.5 3 3.5 4
烤制时间(min) 40 60 80 100 120 140 160 180
若鸡的质量为2.5kg,则估计烤制时间__________分钟.
12.某院观众的座位按下列方式设置,根据表格中两个变量之间的关系,
排数 1 2 3 4 ……
座位数 30 33 36 39 ……
则当时,_____________
13.齿轮每分钟120转,如果表示转数,表示转动时间那么用(分)表示(转)的关系式是_____,其中___为变量,__为常量.
14.王老师开车去加油站加油,发现加油表如图所示.
加油时,单价其数值固定不变,表示“数量”、“金额”的量一直在变化,
在数量 2.45 (升)
金额 16.66 (元)
单价 6.80 (元/升)
这三个量中,____是常量,____是自变量,____是因变量.
三、解答题
15.巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;
(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;
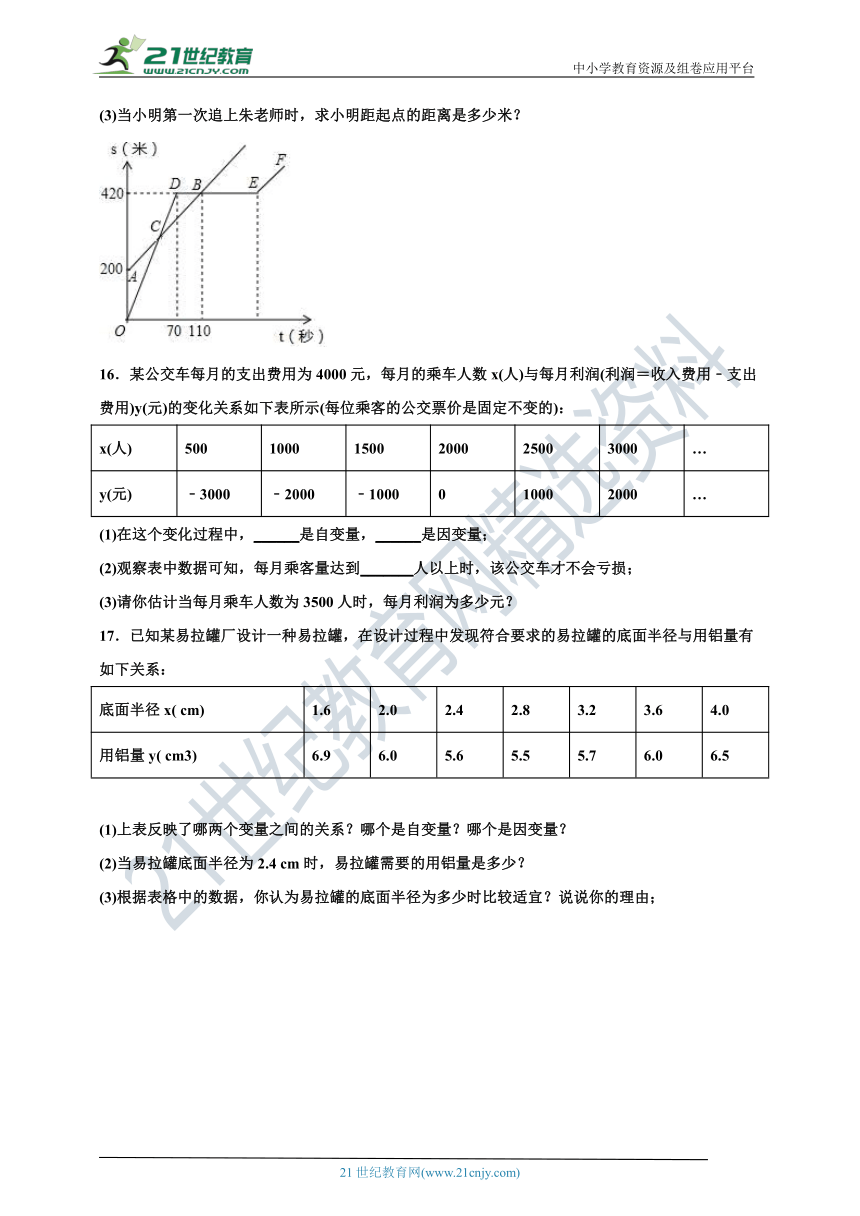
(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
16.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中,______是自变量,______是因变量;
(2)观察表中数据可知,每月乘客量达到_______人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
17.已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如下关系:
底面半径x( cm) 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量y( cm3) 6.9 6.0 5.6 5.5 5.7 6.0 6.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4 cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由;
答案
一、单选题
1.B 2.C 3.C 4.C 5.C 6.D 7.D 8.D
二、填空题
9.20
10.
11.120
12.51
13.n=120t, n、t, 120.
14. 单价 数量 金额
三、解答题
15.【详解】
解:(1)在上述变化过程中,自变量是t,因变量是s;
(2)朱老师的速度=2(米/秒),小明的速度为=6(米/秒);
故答案为t,s;2,6;
(3)设t秒时,小明第一次追上朱老师
根据题意得6t=200+2t,解得t=50(s),
则50×6=300(米),
所以当小明第一次追上朱老师时,小明距起点的距离为300米.
16.【详解】
解:(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为观察表中数据可知,每月乘客量达到2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元.
17.【详解】
(1)反映了易拉罐底面半径和用铝量的关系,其中,易拉罐底面半径为自变量,用铝量为因变量.
(2)当底面半径为2.4 cm时,易拉罐需要的用铝量为5.6 cm3.
(3)易拉罐底面半径为2.8 cm时比较合适,因为此时用铝量较少,成本低.
_21?????????è?????(www.21cnjy.com)_
19.1.1.1变量同步练习
一、单选题
1.在圆的周长C=2πR中,常量与变量分别是( )
A.2是常量,C、π、R是变量 B.2π是常量,C,R是变量
C.C、2是常量,R是变量 D.2是常量,C、R是变量
2.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):
温度/℃ ﹣20 ﹣10 0 10 20 30
声速/m/s 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越高,声速越快
C.当空气温度为20℃时,声音5s可以传播1740m
D.当温度每升高10℃,声速增加6m/s
3.甲以每小时20km的速度行驶时,他所走的路程S(km)与时间t(h)之间可用公式s=20t来表示,则下列说法正确的是( )
A.数20和s,t都是变量 B.s是常量,数20和t是变量
C.数20是常量,s和t是变量 D.t是常量,数20和s是变量
4.我们知道,在弹性限度内,弹簧挂上重物后会伸长.已知一根弹簧的长度与所挂重物的质量之间的关系如下表,则下列说法错误的是( )?
重物的质量 0 1 2 3 4 5
弹簧的长度 12 12.5 13 13.5 14 14.5
A.在这一变化过程中,重物的质量是自变量,弹簧的长度是因变量
B.当所挂重物的质量是时,弹簧的长度是
C.在弹性限度内,当所挂重物的质量是时,弹簧的长度是
D.当不挂重物时,弹簧的长度应为
5.某科研小组在网上获取了声音在空气中传播的速度与空气温度的关系的一些数据(如下表):
气温
声速
下列说法正确的是( )
A.在这个变化中,自变量是声速,因变量是气温
B.温度越高,声速越慢
C.当气温为时,声音可以传播
D.气温每升高,声速减小
6.某商城进一批苹果,在6月27日按照早中晚三个批次销售,销售情况如表,在该变化过程中,常量是( )
A.批次 B.销售量 C.收入 D.单价
7.世纪花园居民小区收取电费的标准是0.6元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
8.设路程为s(km),速度为v(km/h),时间为t(h),当s=60时,v=,在这个函数关系式中( )
A.s是常量,t是s的函数
B.v是常量,t是v的函数
C.t是常量,v是t的函数
D.s是常量,t是自变量,v是t的函数
二、填空题
9.果字成熟后从树上落到地面,它落下的高度与经过的时间有如下的关系:
时间(秒) 0.5 0.6 0.7 0.8 0.9 1
落下的高度(米)
如果果子经过2秒落到地上,那么此果子开始落下时离地面的高度大约是__________米.
10.圆的面积与半径之间的关系是,请指出公式中常量是 ______________________.
11.某烤鸡店在确定烤鸡的烤制时间时,主要依据的是下面表格的数据:
鸡的质量(kg) 0.5 1 1.5 2 2.5 3 3.5 4
烤制时间(min) 40 60 80 100 120 140 160 180
若鸡的质量为2.5kg,则估计烤制时间__________分钟.
12.某院观众的座位按下列方式设置,根据表格中两个变量之间的关系,
排数 1 2 3 4 ……
座位数 30 33 36 39 ……
则当时,_____________
13.齿轮每分钟120转,如果表示转数,表示转动时间那么用(分)表示(转)的关系式是_____,其中___为变量,__为常量.
14.王老师开车去加油站加油,发现加油表如图所示.
加油时,单价其数值固定不变,表示“数量”、“金额”的量一直在变化,
在数量 2.45 (升)
金额 16.66 (元)
单价 6.80 (元/升)
这三个量中,____是常量,____是自变量,____是因变量.
三、解答题
15.巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;
(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;
(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
16.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
x(人) 500 1000 1500 2000 2500 3000 …
y(元) ﹣3000 ﹣2000 ﹣1000 0 1000 2000 …
(1)在这个变化过程中,______是自变量,______是因变量;
(2)观察表中数据可知,每月乘客量达到_______人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
17.已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如下关系:
底面半径x( cm) 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量y( cm3) 6.9 6.0 5.6 5.5 5.7 6.0 6.5
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当易拉罐底面半径为2.4 cm时,易拉罐需要的用铝量是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少时比较适宜?说说你的理由;
答案
一、单选题
1.B 2.C 3.C 4.C 5.C 6.D 7.D 8.D
二、填空题
9.20
10.
11.120
12.51
13.n=120t, n、t, 120.
14. 单价 数量 金额
三、解答题
15.【详解】
解:(1)在上述变化过程中,自变量是t,因变量是s;
(2)朱老师的速度=2(米/秒),小明的速度为=6(米/秒);
故答案为t,s;2,6;
(3)设t秒时,小明第一次追上朱老师
根据题意得6t=200+2t,解得t=50(s),
则50×6=300(米),
所以当小明第一次追上朱老师时,小明距起点的距离为300米.
16.【详解】
解:(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
故答案为每月的乘车人数x,每月的利润y;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
故答案为观察表中数据可知,每月乘客量达到2000;
(3)由表中数据可知,每月的乘车人数每增加500人,每月的利润可增加1000元,
当每月的乘车人数为2000人时,每月利润为0元,则当每月乘车人数为3500人时,每月利润为3000元.
17.【详解】
(1)反映了易拉罐底面半径和用铝量的关系,其中,易拉罐底面半径为自变量,用铝量为因变量.
(2)当底面半径为2.4 cm时,易拉罐需要的用铝量为5.6 cm3.
(3)易拉罐底面半径为2.8 cm时比较合适,因为此时用铝量较少,成本低.
_21?????????è?????(www.21cnjy.com)_
