18.2.2 菱形(第二课时 菱形的判定) 课件(共17张PPT)
文档属性
| 名称 | 18.2.2 菱形(第二课时 菱形的判定) 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 12:44:16 | ||
图片预览





文档简介
18.2.2 菱形
第二课时 菱形的判定
第十八章 平行四边形
2021年春人教版八年级(下)数学
学习目标
1、理解菱形的判定定理。
2、尝试对菱形判定定理的证明。
3、能利用菱形的判定定理解决简单问题。
理解并掌握菱形的判定定理。(重点)
能利用菱形的判定定理解决简单问题。(难点)
知识回顾
菱形的知识点回顾
概念:
注意事项:
菱形的性质:
有一组邻边相等的平行四边形叫菱形。
1)菱形是一种特殊的平行四边形。
2)平行四边形不一定是菱形。
菱形的两组对边分别相等;
菱形对角线互相平分;
菱形的两组对角分别相等;
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
本节课我们学习如何判定一个平行四边形或四边形是菱形
A
B
D
C
探索思考
菱形性质的逆命题:
两组对边分别相等的四边形是菱形
两组对角分别相等的四边形是菱形
对角线互相平分的四边形是菱形
四条边都相等的四边形是菱形
【思考】菱形性质的逆命题是否成立,请举出反例?
前三个逆命题不一定成立,当条件成立时,结论可能是平行四边形,可能是矩形,可能是菱形。
本节课我们讨论
这两个逆命题是否成立
对角线互相垂直的的平行四边形是菱形
探索思考
已知线段AC,你能利用尺规作四边形ABCD,要求四边形的四条边相等?
C
A
做法:分别以A、C为圆心,以大于?????????AC的长为半径作弧,两条弧分别相交于点B , D,依次连接A、B、C、D四点.
?
D
B
[思考]得到的这个四边形是菱形吗?
探索证明
四条边都相等的四边形是菱形
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵AB=BC=CD=AD
∴AB=CD,BC=AD
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形
A
B
D
C
判定1:四条边都相等的四边形是菱形
探索证明
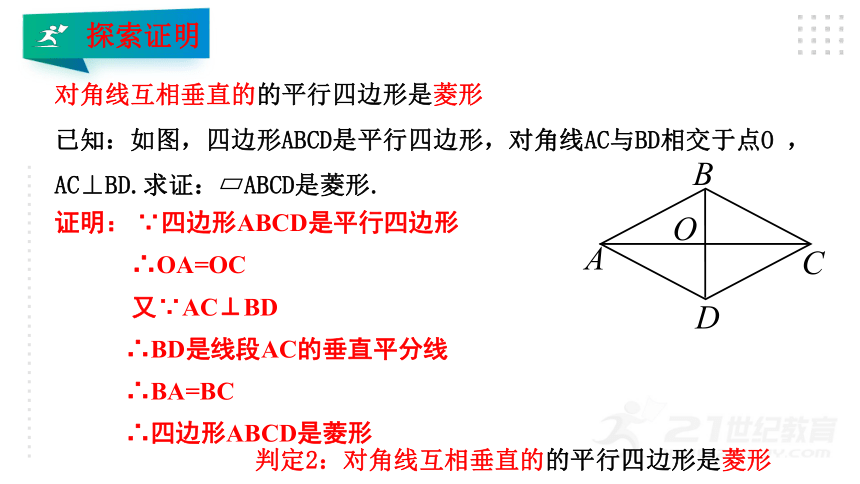
对角线互相垂直的的平行四边形是菱形
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.求证:?ABCD是菱形.
A
B
C
O
D
证明: ∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴四边形ABCD是菱形
判定2:对角线互相垂直的的平行四边形是菱形
针对练习
如图,?四边形ABCD的两条对角线AC、BD相交于点O,AB=10,AO=8,BO=6.
求证:四边形ABCD是菱形.
A
B
C
D
O
证明:∵ OA=8,OB=6,AB=10
∴ AB2=OA2+OB2
∴△AOB是直角三角形
即AC⊥BD
又∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
课堂练习
1.已知四边形ABCD是平行四边形,下列结论中正确的有( )
①当AB=BC时,四边形ABCD是菱形; ②当AC⊥BD时,四边形ABCD是菱形;
③当∠ABC=90°时,四边形ABCD是菱形: ④当AC=BD时,四边形ABCD是菱形;
A.3个 B.4个 C.1个 D.2个
【详解】
解:
∵四边形ABCD是平行四边形,
∴①当AB=BC时,四边形ABCD是菱形;故符合题意;
②当AC⊥BD时,四边形ABCD是菱形;故符合题意;
③当∠ABC=90°时,四边形ABCD是矩形;故不符合题意;
④当AC=BD时,四边形ABCD是矩形;故不符合题意;
故选:D.
2.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
【详解】
如图:连接AC、BD,在△ABD中,
∵AH=HD,AE=EB ∴EH=????????BD,
同理FG=????????BD,HG=????????AC,EF=????????AC,
又∵在矩形ABCD中,AC=BD
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
?
课堂练习
3.如图,????、????、????、????分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,则四边形ABCD应具备的条件是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.一组对边平行而另一组对边不平行
?
【详解】
解:连接AC,BD,
∵四边形ABCD中,E、F、G、H分别是四条边的中点,要使四边形EFGH为菱形,
∴EF=FG=GH=EH,
∵FG=EH=????????DB,HG=EF=????????AC,
∴要使EH=EF=FG=HG,
∴BD=AC,
∴四边形ABCD应具备的条件是BD=AC,
故选C.
?
课堂练习
课堂练习
4. 如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
?A.∠1=∠2 B.BE=DF C.∠EDF=60° D.AB=AF
【详解】
由正方形的性质知,∠ACD=∠ACB=45°,BC=CD,CF=CF,
∴△CDF≌△CBF,
∴BF=FD,
同理,BE=ED,
∴当BE=DF,有BF=FD=BE=ED,四边形BEDF是菱形.
故选B.
课堂练习
5,变式3-1 某花木场有一块如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,用篱笆围成的四边形EFGH场地的周长为40cm,则对角线????????=________.
?
【详解】
连接BD
∵四边形ABCD是等腰梯形 ∴AC=BD
∵各边的中点分别是E、F、G、H
∴HG=????????AC=EF,EH=????????BD=FG
∴HG=EH=EF=FG,
∴四边形EFGH是菱形
∵四边形EFGH场地的周长为40cm
∴EF=10cm
∴AC=20cm
?
课堂练习
6.如图,在?ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF,求证:四边形AECF是菱形.
【证明】
∵四边形????????????????是平行四边形,
∴????????=????????,????????//????????,
而????????=????????,
∴????????=????????而????????//????????,
∴四边形????????????????是平行四边形,
∵????????⊥????????,
∴四边形????????????????是菱形.
?
7.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
1)求证:四边形BCFE是菱形;
2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
解:1)∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC.
∴四边形BCFE是平行四边形.
又∵BE=FE,
∴四边形BCFE是菱形.
2)过点E,做EO⊥BC于点O
∵∠BCF=120°∴∠EBC=60°
∴△EBC是等边三角形.而CE=4,则OC=2
∴????????=????????.
∴菱形的面积为4×????????=????????.
?
o
课堂练习
https://www.21cnjy.com/help/help_extract.php
第二课时 菱形的判定
第十八章 平行四边形
2021年春人教版八年级(下)数学
学习目标
1、理解菱形的判定定理。
2、尝试对菱形判定定理的证明。
3、能利用菱形的判定定理解决简单问题。
理解并掌握菱形的判定定理。(重点)
能利用菱形的判定定理解决简单问题。(难点)
知识回顾
菱形的知识点回顾
概念:
注意事项:
菱形的性质:
有一组邻边相等的平行四边形叫菱形。
1)菱形是一种特殊的平行四边形。
2)平行四边形不一定是菱形。
菱形的两组对边分别相等;
菱形对角线互相平分;
菱形的两组对角分别相等;
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
本节课我们学习如何判定一个平行四边形或四边形是菱形
A
B
D
C
探索思考
菱形性质的逆命题:
两组对边分别相等的四边形是菱形
两组对角分别相等的四边形是菱形
对角线互相平分的四边形是菱形
四条边都相等的四边形是菱形
【思考】菱形性质的逆命题是否成立,请举出反例?
前三个逆命题不一定成立,当条件成立时,结论可能是平行四边形,可能是矩形,可能是菱形。
本节课我们讨论
这两个逆命题是否成立
对角线互相垂直的的平行四边形是菱形
探索思考
已知线段AC,你能利用尺规作四边形ABCD,要求四边形的四条边相等?
C
A
做法:分别以A、C为圆心,以大于?????????AC的长为半径作弧,两条弧分别相交于点B , D,依次连接A、B、C、D四点.
?
D
B
[思考]得到的这个四边形是菱形吗?
探索证明
四条边都相等的四边形是菱形
已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵AB=BC=CD=AD
∴AB=CD,BC=AD
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形
A
B
D
C
判定1:四条边都相等的四边形是菱形
探索证明
对角线互相垂直的的平行四边形是菱形
已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交于点O ,AC⊥BD.求证:?ABCD是菱形.
A
B
C
O
D
证明: ∵四边形ABCD是平行四边形
∴OA=OC
又∵AC⊥BD
∴BD是线段AC的垂直平分线
∴BA=BC
∴四边形ABCD是菱形
判定2:对角线互相垂直的的平行四边形是菱形
针对练习
如图,?四边形ABCD的两条对角线AC、BD相交于点O,AB=10,AO=8,BO=6.
求证:四边形ABCD是菱形.
A
B
C
D
O
证明:∵ OA=8,OB=6,AB=10
∴ AB2=OA2+OB2
∴△AOB是直角三角形
即AC⊥BD
又∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
课堂练习
1.已知四边形ABCD是平行四边形,下列结论中正确的有( )
①当AB=BC时,四边形ABCD是菱形; ②当AC⊥BD时,四边形ABCD是菱形;
③当∠ABC=90°时,四边形ABCD是菱形: ④当AC=BD时,四边形ABCD是菱形;
A.3个 B.4个 C.1个 D.2个
【详解】
解:
∵四边形ABCD是平行四边形,
∴①当AB=BC时,四边形ABCD是菱形;故符合题意;
②当AC⊥BD时,四边形ABCD是菱形;故符合题意;
③当∠ABC=90°时,四边形ABCD是矩形;故不符合题意;
④当AC=BD时,四边形ABCD是矩形;故不符合题意;
故选:D.
2.顺次连接矩形的四边形中点所得的四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
【详解】
如图:连接AC、BD,在△ABD中,
∵AH=HD,AE=EB ∴EH=????????BD,
同理FG=????????BD,HG=????????AC,EF=????????AC,
又∵在矩形ABCD中,AC=BD
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选:C.
?
课堂练习
3.如图,????、????、????、????分别是四边形ABCD四条边的中点,要使四边形EFGH为菱形,则四边形ABCD应具备的条件是( )
A.对角线互相平分 B.对角线互相垂直
C.对角线相等 D.一组对边平行而另一组对边不平行
?
【详解】
解:连接AC,BD,
∵四边形ABCD中,E、F、G、H分别是四条边的中点,要使四边形EFGH为菱形,
∴EF=FG=GH=EH,
∵FG=EH=????????DB,HG=EF=????????AC,
∴要使EH=EF=FG=HG,
∴BD=AC,
∴四边形ABCD应具备的条件是BD=AC,
故选C.
?
课堂练习
课堂练习
4. 如图所示,正方形ABCD中,E,F是对角线AC上两点,连接BE,BF,DE,DF,则添加下列哪一个条件可以判定四边形BEDF是菱形( )
?A.∠1=∠2 B.BE=DF C.∠EDF=60° D.AB=AF
【详解】
由正方形的性质知,∠ACD=∠ACB=45°,BC=CD,CF=CF,
∴△CDF≌△CBF,
∴BF=FD,
同理,BE=ED,
∴当BE=DF,有BF=FD=BE=ED,四边形BEDF是菱形.
故选B.
课堂练习
5,变式3-1 某花木场有一块如等腰梯形ABCD的空地(如图),各边的中点分别是E、F、G、H,用篱笆围成的四边形EFGH场地的周长为40cm,则对角线????????=________.
?
【详解】
连接BD
∵四边形ABCD是等腰梯形 ∴AC=BD
∵各边的中点分别是E、F、G、H
∴HG=????????AC=EF,EH=????????BD=FG
∴HG=EH=EF=FG,
∴四边形EFGH是菱形
∵四边形EFGH场地的周长为40cm
∴EF=10cm
∴AC=20cm
?
课堂练习
6.如图,在?ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF,求证:四边形AECF是菱形.
【证明】
∵四边形????????????????是平行四边形,
∴????????=????????,????????//????????,
而????????=????????,
∴????????=????????而????????//????????,
∴四边形????????????????是平行四边形,
∵????????⊥????????,
∴四边形????????????????是菱形.
?
7.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
1)求证:四边形BCFE是菱形;
2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
解:1)∵D、E分别是AB、AC的中点,∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC.
∴四边形BCFE是平行四边形.
又∵BE=FE,
∴四边形BCFE是菱形.
2)过点E,做EO⊥BC于点O
∵∠BCF=120°∴∠EBC=60°
∴△EBC是等边三角形.而CE=4,则OC=2
∴????????=????????.
∴菱形的面积为4×????????=????????.
?
o
课堂练习
https://www.21cnjy.com/help/help_extract.php
