9.4矩形、菱形、正方形同步培优卷(Word版 含解析)
文档属性
| 名称 | 9.4矩形、菱形、正方形同步培优卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 473.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览


文档简介
9.4矩形、菱形、正方形同步培优卷
1.如图,正方形ABCD中,在BA延长线上取一点,使BE=BD,连接DE,则∠EDA的度数为( )
A.10° B.15° C.30° D.22.5°
2.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
3.下列结论中,菱形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对边相等且平行
4.如图,点E为矩形ABCD的边BC长上的点,作DF⊥AE于点F,且满足DF=AB.下面结论:①DE平分∠AEC;②△ADE为等腰三角形;③AF=AB;
④AE=BE+EF.其中正确的结论有多少个( )
A.1个 B.2个 C.3个 D.4个
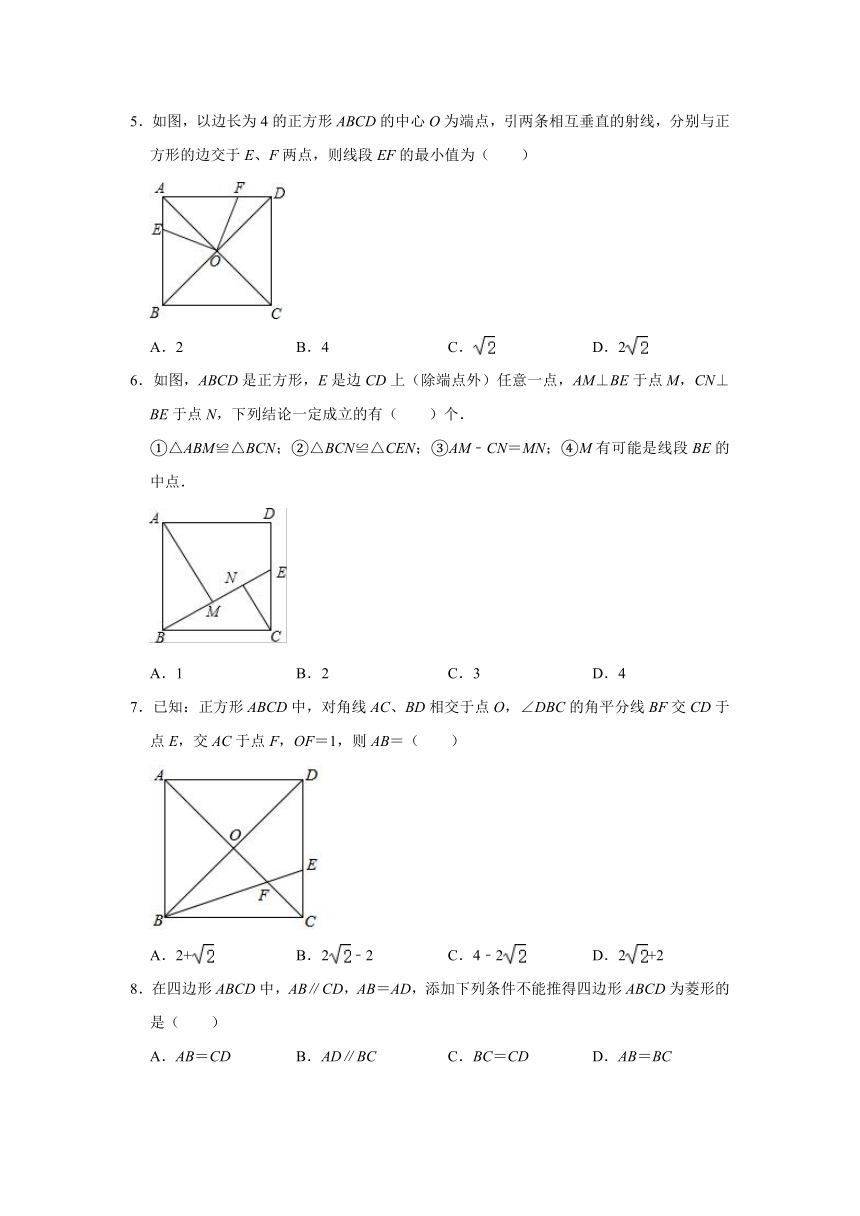
5.如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
6.如图,ABCD是正方形,E是边CD上(除端点外)任意一点,AM⊥BE于点M,CN⊥BE于点N,下列结论一定成立的有( )个.
①△ABM≌△BCN;②△BCN≌△CEN;③AM﹣CN=MN;④M有可能是线段BE的中点.
A.1 B.2 C.3 D.4
7.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的角平分线BF交CD于点E,交AC于点F,OF=1,则AB=( )
A.2+ B.2﹣2 C.4﹣2 D.2+2
8.在四边形ABCD中,AB∥CD,AB=AD,添加下列条件不能推得四边形ABCD为菱形的是( )
A.AB=CD B.AD∥BC C.BC=CD D.AB=BC
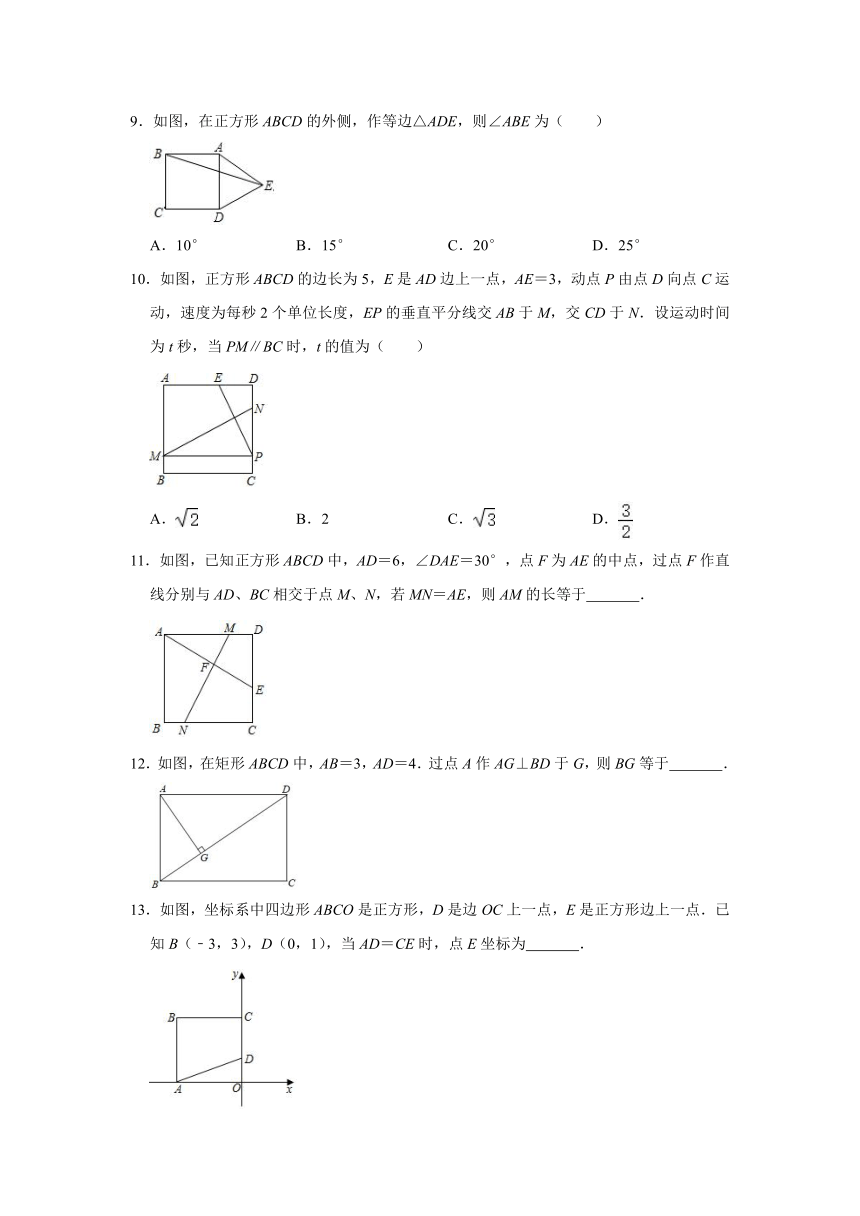
9.如图,在正方形ABCD的外侧,作等边△ADE,则∠ABE为( )
A.10° B.15° C.20° D.25°
10.如图,正方形ABCD的边长为5,E是AD边上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线交AB于M,交CD于N.设运动时间为t秒,当PM∥BC时,t的值为( )
A. B.2 C. D.
11.如图,已知正方形ABCD中,AD=6,∠DAE=30°,点F为AE的中点,过点F作直线分别与AD、BC相交于点M、N,若MN=AE,则AM的长等于 .
12.如图,在矩形ABCD中,AB=3,AD=4.过点A作AG⊥BD于G,则BG等于 .
13.如图,坐标系中四边形ABCO是正方形,D是边OC上一点,E是正方形边上一点.已知B(﹣3,3),D(0,1),当AD=CE时,点E坐标为 .
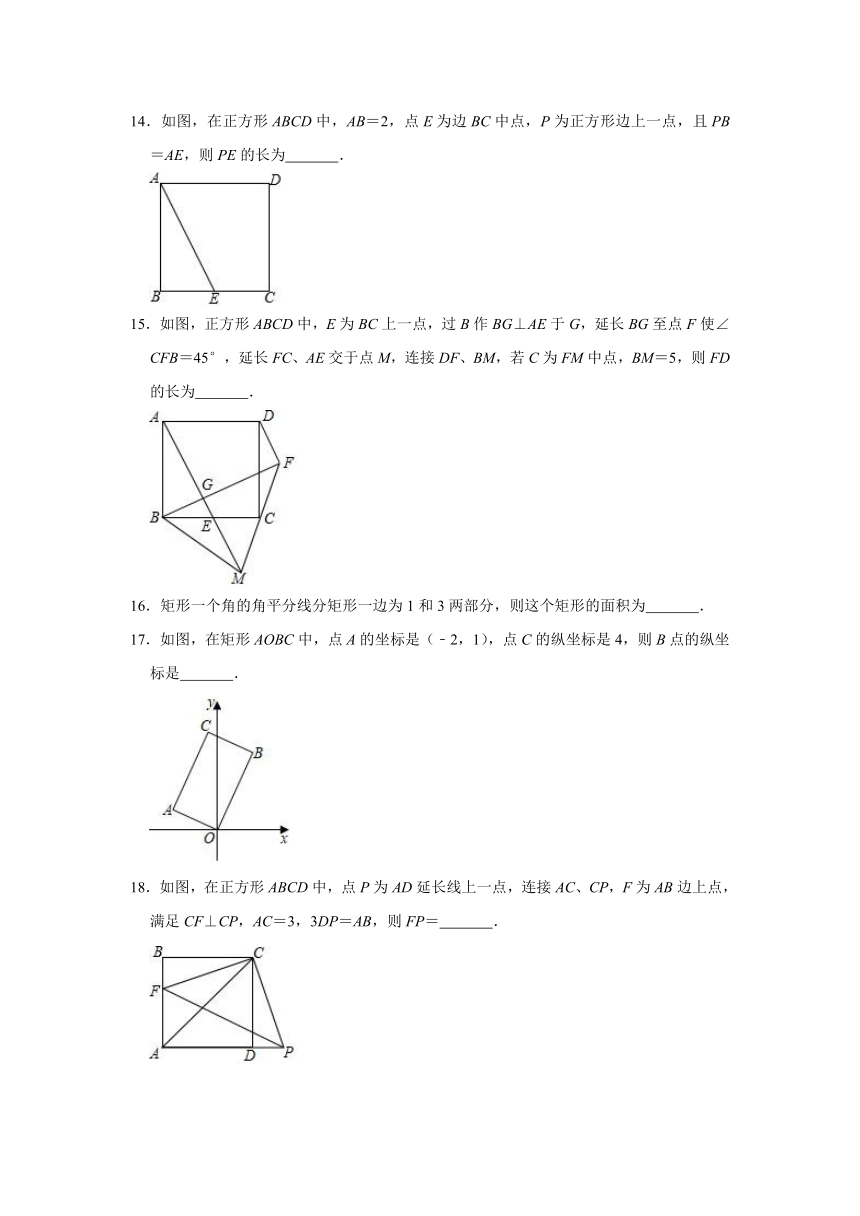
14.如图,在正方形ABCD中,AB=2,点E为边BC中点,P为正方形边上一点,且PB=AE,则PE的长为 .
15.如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°,延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=5,则FD的长为 .
16.矩形一个角的角平分线分矩形一边为1和3两部分,则这个矩形的面积为 .
17.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B点的纵坐标是 .
18.如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上点,满足CF⊥CP,AC=3,3DP=AB,则FP= .
19.已知矩形ABCD的对角线相交于点O,AE平分∠BAD交矩形的边于点E,若∠CAE=10°,则∠AOB的度数为 .
20.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
21.如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF;
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE的周长.
22.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)若∠B=30°,AC=6,求CE的长;
(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明原因.
23.如图,正方形ABCD中,点E在BC边上,AF平分∠DAE,DF∥AE,AF与CD相交于点G.
(1)如图1,当∠AEC=120°,AE=4时,求FG的长;
(2)如图2,在AB边上截取点H,使得DH=AE,DH与AF、AE,分别交于点M、N,求证:AE=AH+DG.
24.如图①,正方形ABCD中,M是AB的中点,E是延长线上一点.MN⊥DM,且交∠CBE的平分线于N.
(1)若点F是AD的中点,求证:MD=MN;
(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任意一点”,其它条件不变.如图②所示,则结论“MD=MN”是否成立.若成立,给出证明;若不成立,请说明理由.
25.如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD,
(1)求证:AO=EO;
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
26.在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
(1)如图1,若PB=a,AB=3a,求线段MN的长度;
(2)用等式表示ME、EF、NF之间的数量关系并证明.
27.如图,点G是正方形ABCD对角线CA的延长线一点,对角线BD与AC交于点O,以线段AG为边作一个正方形AEFG,连接EB、GD.
(1)求证:EB=GD;
(2)若AB=5,AG=2,求EB的长.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠ABD=45°=∠ADB,
∵BE=BD,
∴∠BDE=67.5°,
∴∠EDA=∠BDE﹣∠ADB=22.5°,
故选:D.
2.解:如图,当点M在BC上时,
∵△ABM′和△DCE全等,
∴BM=CE,
由题意得:BM′=2t﹣4=3,
所以t=3.5(秒);
当点M在AD上时,
∵△ABM″和△CDE全等,
∴AM″=CE,
由题意得:AM″=16﹣2t=3,
解得t=6.5(秒).
所以,当t的值为3.5秒或6.5秒时.△ABM和△DCE全等.
故选:D.
3.解:A.因为矩形的对角线相等,所以A选项不符合题意;
B.因为矩形和菱形的对角线都互相平分,所以B选项不符合题意;
C.因为菱形对角线互相垂直,所以C选项符合题意;
D.因为矩形和菱形的对边都相等且平行,不符合题意.
故选:C.
4.解:∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,AD∥BC,AB=CD,
∵DF=AB,
∴DF=CD,
∵DF⊥AE,
∴∠DFA=∠DFE=90°,
在Rt△DEF和Rt△DEC中,,
∴Rt△DEF≌Rt△DEC(HL),
∴∠FED=∠CED,
∴DE平分∠AEC;
故①正确;
∵AD∥BC,
∴∠AEB=∠DAF,
在△ABE和△AFD中,
,
∴△ABE≌△AFD(AAS),
∴AE=AD,
∴△ADE为等腰三角形;
故②正确;
∵△ABE≌△DFA,
∴不存在AF=AB,
故③错误;
∵△ABE≌△DFA,
∴BE=FA,
∴AE=AF+EF=BE+EF.
故④正确.
故正确的结论有①②④,三个.
故选:C.
5.解:如图,连接EF,
∵四边形ABCD为正方形,
∴∠EAO=∠FDO=45°,AO=DO;
∵∠EOF=90°,∠AOD=90°,
∴∠AOE=∠DOF;
在△AOE与△DOF中,
,
∴△AOE≌△DOF(ASA),
∴OE=OF(设为λ);
∴△EOF是等腰直角三角形,
由勾股定理得:
EF2=OE2+OF2=2λ2;
∴EF=OE=λ,
∵正方形ABCD的边长是4,
∴OA=2,O到AB的距离等于2(O到AB的垂线段的长度),
由题意可得:2≤λ≤2,
∴2≤EF≤4.
所以线段EF的最小值为2.
故选:D.
6.解:①∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∴∠ABM+∠NBC=90°,
∵AM⊥BE于点M,CN⊥BE于点N,
∴∠AMB=∠BNC=90°,
∴∠ABM+∠BAM=90°,
∴∠NBC=∠BAM,
∴△ABM≌△BCN;
故①正确;
②∵∠BCE=∠CNE=90°,∠CEN=∠CEB,
∵CE≠BE,
∴△BCN∽△CEN,
故②不正确;
③∵△ABM≌△BCN,
∴AM=BN,BM=CN,
∴MN=BN﹣BM=AM﹣CN,
故③正确;
④当M是线段BE的中点时,E在点D处,而已知中E是边CD上(除端点外)任意一点,
所以M不可能是线段BE的中点.
故④不正确;
所以正确的有:①③2个,
故选:B.
7.解:如图,作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴AB=BC=OB=2+.
故选:A.
8.解:A选项:若AB=CD,∵AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
B选项:当AD∥BC时,又AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
C选项:当BC=CD时,△ABC≌△ACD(SAS),
∴∠A=∠C.
∵AB∥CD,
∴∠C+∠ABC=180°.
∴∠A+∠ABC=180°.
∴AD∥BC.
又AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
D选项只能说明四边形的三条边相等,所以不能判定是菱形.
故选:D.
9.解:∵四边形ABCD为正方形,△ADE为等边三角形,
∴AB=BC=CD=AD=AE=DE,∠BAD=90°,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,
又∵AB=AE,
∴∠ABE=(180°﹣150°)=15°.
故选:B.
10.解:如图,连接ME,
∵MN垂直平分PE,
∴MP=ME,
当MP∥BC时,四边形BCPM是矩形,
∴BC=MP=5,
∴ME=5,
又∵AE=3,
∴AM=4=DP,
∴t=4÷2=2(s),
故选:B.
11.解:在正方形ABCD中,AD=6,∠DAE=30°,
设DE=x,则AE=2x,由勾股定理x2+62=(2x)2,
解得:x=2(负值舍去),
∴AE=4,
∵点F为AE的中点,
∴AF=EF=2,
分两种情况:
①过M作MG⊥BC,G为垂足,则MG=DC=AD,
在Rt△MGN和Rt△ADE中,
,
∴Rt△MGN≌Rt△ADE(HL),
∴∠NMG=∠EAD,
∴∠NMG+∠AMF=90°,
∴∠EAD+∠AMF=90°,
∴∠AFM=90°,
在Rt△AFM中,∠DAE=30°,AF=2,
设MF=m,则AM=2m,
由勾股定理,得
4m2﹣m2=12,
解得m=2(负值舍去),则AM=4;
②如图,过N作NG⊥AD于G,过M作MH⊥AE于H,
则NG=CD=AD,
在Rt△ADE和Rt△NGM中,
,
∴Rt△ADE≌Rt△NGM(HL),
∴∠GNM=∠DAE=30°,
∴∠GMN=60°,
△AMF中,∠GMN=∠MAF+∠AFM,
∴∠AFM=∠DAE=30°,
∴AM=MF,
∵MH⊥AF,
∴AH=FH,
设MH=x,则AM=2x,AH=FH=x,
∵F是AE的中点,
∴AE=2AF=4AH=4x,
Rt△ADE中,∠DAE=30°,
∴DE=AE=2x,AD=DE=6x,
∵AD=6,即6x=6,
x=1,即AM=2x=2;
故答案为:4或2.
12.解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∴BD===5,
由三角形的面积公式得,BD?AG=AB?AD,
∴AG===,
∴BG===,
故答案为:.
13.解:如图,符合条件的点有两个,当点E在边AB和边OA上时,设为点E′和点E″,
∵B(﹣3,3),D(0,1),
∴AB=OA=3,OD=1,
∵四边形ABCO是正方形,
∴AB=BC=OC=OA=3,∠B=∠AOD=90°,
∵AD=CE′=CE″,
在Rt△BCE′和Rt△OAD中,
,
∴Rt△BCE′≌Rt△OAD(HL),
∴BE′=OD=1,
∴AE′=AB﹣BE′=2,
∴E′(﹣3,2);
同理Rt△OCE′≌Rt△OAD(HL),
∴OE″=OD=1,
∴E′(﹣1,0).
所以点E坐标为(﹣3,2)或(﹣1,0).
故答案为:(﹣3,2)或(﹣1,0).
14.解:当点P在AD边上时,
∵PB=AE,点E为边BC中点,
∴点P为边AD中点,
∴PE=AB=2;
当点P在CD边上时,
∵PB=AE,点E为边BC中点,
∴点P为边CD中点,
∴PE===.
所以PE的长为:2或.
故答案为:2或.
15.解:如图,过C点作CH⊥BF于H点,过B点作BK⊥CM于K,过D作DQ⊥MF交MF延长线于Q.
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°,
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC(AAS),
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=GM,
∴BG=GM,
∵BM=5,
∴BG=,GM=2,
∴AG=2,AB=5,
∴HF=,
∴CF=×=,
∴CM=,
∵CK=CM=CF=,
∴BK=,
∵在△BKC和△CQD中,
∵∠CBK=∠DCQ,∠BKC=∠CQD=90°,BC=CD,
∴△BKC≌△CQD(AAS),
∴CQ=BK=,
DQ=CK=,
∴QF=CQ﹣CF=﹣=,
∴DQ=QF=,
∴DF=×=.
故答案为.
16.解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
①如图,当AE=3时,AB=3,AD=1+3=4,
此时矩形的面积是:3×4=12;
②同理可得,当AE=1时,AB=1,AD=4,
此时矩形的面积是1×4=4;
故答案为:4或12.
17.解:如图,
过点A作AD⊥x轴于点D,
过点B作BE⊥x轴于点E,
过点C作CF∥y轴,过点A作AF∥x轴,交点为F,
则AF⊥CF,
延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴OB=AC,AC∥OB,
∴∠CAF=∠CHO=∠BOE,
∵∠AFC=∠OEB=90°,
∴△AFC≌△OEB(AAS),
∴CF=BE=4﹣1=3,
故答案为:3.
18.解:∵四边形ABCD是正方形,
∴AB=CB=CD=AD,
∠CBF=∠CDP=∠BCF+∠FCD=90°,
又∵CF⊥CP,
∴∠DCP+∠FCD=90°,
∴∠BCF=∠DCP,
在△BCF和△DCP中,
∴△BCF≌△DCP(AAS),
∴BF=DP,
∵AC=3,∠ABC=90°,AB=BC,
∴2AB2=AC2=32=9
∴AB=,
∴AD=,
∵3DP=AB,
∴DP=,
∴BF=DP=,
∴AF=AB﹣BF=﹣=,
AP=AD+DP=+=2,
在Rt△AFP中,
FP===.
故答案为:.
19.解:由题得,画出如下示意图:
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OB=OD,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∵∠CAE=10°,
由图(1)得:∠BAO=∠BAE+∠EAC=45°+10°=55°,
又∵OA=OB,
∴∠BAO=∠OBA=55°,
∴∠AOB=180°﹣55°﹣55°=70°,
由图(2)得:∠DAO=∠DAE+∠EAC=45°+10°=55°,
又∵OA=OD,
∴∠OAD=∠ODA=55°,
∴∠AOB=∠OAD+∠ODA=110°,
综上所述:∠AOB的值为:70°、110°,
故答案为:70°、110°.
20.解:∵矩形ABCD中,AB=4,AD=3=BC,
∴Rt△ACD中,AC==5,
又∵AQ=AD=3,AD∥CP,
∴CQ=5﹣3=2,∠CQP=∠AQD=∠ADQ=∠CPQ,
∴CP=CQ=2,
∴BP=3﹣2=1,
∴Rt△ABP中,AP===,
故答案为:.
21.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,DO=BO,
∴∠EDO=∠FBO,
又∵EF⊥BD,
∴∠EOD=∠FOB=90°,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA);
(2)解:∵由(1)可得,ED∥BF,ED=BF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形,
根据AB=6,AD=8,设AE=x,可得BE=ED=8﹣x,
在Rt△ABE中,根据勾股定理可得:BE2=AB2+AE2,
即(8﹣x)2=x2+62,
解得:,
∴,
∴四边形BFDE的周长=.
22.解:(1)∵∠ACB=90°,∠B=30°,
∴∠CAB=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
∵AF平分∠CAB,
∴∠CAF=∠BAF=30°,
∴CE=AE,
过点E用EH垂直于AC于点H,
∴CH=AH
∵AC=6,
∴CE=2
答:CE的长为2;
(2)∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF,
在Rt△ACF与Rt△AGF中,
AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,
∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=FG,
∴四边形CEGF是菱形
23.解:(1)∵∠AEC=120°,
∴∠AEB=180°﹣120°=60°,
∵四边形ABCD是正方形,
∴∠B=∠BAD=∠ADC=90°,AD∥BC,
∴∠BAE=30°,∠DAE=∠AEB=60°,
∵AF平分∠DAE,
∴∠DAF=∠EAF=30°,
Rt△ABE中,AE=4,∠BAE=30°,
∴BE=2,AB=AD=2,
Rt△ADG中,∠DAG=30°,
∴DG=2,
∵DF∥AE,
∴∠F=∠EAF=30°,
∵∠AGD=60°,
∴∠GDF=∠F=30°,
∴GF=DG=2;
(2)由(1)知:∠F=∠DAF,
∴AD=DF,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=90°,
∵AE=DH,
∴Rt△DAH≌Rt△ABE(HL),
∴∠BAE=∠ADH,
∵∠BAE+∠DAE=∠ADH+∠DAE=90°,
∴∠AND=90°,
∵DF∥AE,
∴∠HDF=∠HNE=90°,
∴∠MDG+∠GDF=∠ADM+∠MDG=90°,
∴∠ADM=∠GDF,
∴△ADM≌△FDG(ASA),
∴DM=DG,
∴∠DMG=∠DGM,
∵AH∥DG,
∴∠HAM=∠DGM,
∵∠AMH=∠DMG,
∴∠HAM=∠AMH,
∴AH=HM,
∴DH=HM+DM=AH+DG=AE.
24.解:(1)如图,取AD的中点F,连接FM.
∵∠FDM+∠DMA=∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∵AF=AD=AB=AM=MB=DF,
∵BN平分∠CBE,即∠NBE=∠CBE=45°,
又∵AM=AF,
∴∠AFM=45°,
∴∠DFM=∠MBN=135°.
∵DF=MB,
在△DFM和△MBN中
,
∴△DFM≌△MBN(ASA).
∴DM=MN.
(2)结论“DM=MN”仍成立.
证明如下:如图,在AD上截取AF'=AM,连接F'M.
∵DF'=AD﹣AF',MB=AB﹣AM,AD=AB,AF'=AM,
∴DF'=MB.
∵∠F'DM+∠DMA=∠BMN+∠DMA=90°,
∴∠F'DM=∠BMN.
又∠DF'M=∠MBN=135°,
在△DF'M和△MBN中
,
∴△DF'M≌△MBN(ASA).
∴DM=MN.
25.解:(1)证明:∵AD∥BC,
∴∠CBD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
又∵AE⊥BD,
∴BO=DO,
又∵∠AOD=∠EOB,
∴△AOD≌△EOB,
∴AO=EO;
(2)当△ABC满足∠ABC=90°时,四边形AECD是正方形.理由:
∵△AOD≌△EOB,
∴AD=BE,
又∵AD∥BE,AE⊥BD,
∴四边形ABED是菱形,
∴当∠ABC=90°时,菱形ABED是正方形,
即当△ABC满足∠ABC=90°时,四边形AECD是正方形.
26.解:(1)如图所示,过N作NG⊥AB,交AB于点G. 则四边形AGND是矩形,所以NG=AD=AB=3a,
∵MN⊥AP∴∠MNG=∠PAB 且∠PBA=∠NGMAB=NG∴△ABP≌△NGM
∴MN=AP==
(2)如图所示,过P作PH∥AB,过F作ST∥AB,连接AF,PF
∵NM垂直平分AP,则AE=PE,∠AEM=∠PEH=90°,
∵PH∥AB∴∠PHE=∠MEA,∠HPE=∠MAE
∴△AME≌△PHE
∴ME=HE
∠TDF=∠FBP=45°
∴TD=TF,FS=BS
∵BS=AT=FS
∵点F在线段AP的垂直平分线上,
∴FP=FA
∴Rt△FPS≌Rt△ATF
∴PS=TF=TD=SC=PS
∵PH∥TS∥CD
∴HF=FN
∴ME+NF=EF
27.(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
在△GAD和△EAB中,
∴△GAD≌△EAB,
∴EB=GD;
(2)∵四边形ABCD是正方形,AB=5,
∴BD⊥AC,AC=BD=5,
∴∠DOG=90°,OA=OD=BD=,
∵AG=2,
∴OG=OA+AG=,
由勾股定理得,GD==,
∴EB=.
1.如图,正方形ABCD中,在BA延长线上取一点,使BE=BD,连接DE,则∠EDA的度数为( )
A.10° B.15° C.30° D.22.5°
2.如图,在正方形ABCD中,AB=4,E是BC上的一点且CE=3,连接DE,动点M从点A以每秒2个单位长度的速度沿AB﹣BC﹣CD﹣DA向终点A运动,设点M的运动时间为t秒,当△ABM和△DCE全等时,t的值是( )
A.3.5 B.5.5 C.6.5 D.3.5或6.5
3.下列结论中,菱形具有而矩形不一定具有的性质是( )
A.对角线相等 B.对角线互相平分
C.对角线互相垂直 D.对边相等且平行
4.如图,点E为矩形ABCD的边BC长上的点,作DF⊥AE于点F,且满足DF=AB.下面结论:①DE平分∠AEC;②△ADE为等腰三角形;③AF=AB;
④AE=BE+EF.其中正确的结论有多少个( )
A.1个 B.2个 C.3个 D.4个
5.如图,以边长为4的正方形ABCD的中心O为端点,引两条相互垂直的射线,分别与正方形的边交于E、F两点,则线段EF的最小值为( )
A.2 B.4 C. D.2
6.如图,ABCD是正方形,E是边CD上(除端点外)任意一点,AM⊥BE于点M,CN⊥BE于点N,下列结论一定成立的有( )个.
①△ABM≌△BCN;②△BCN≌△CEN;③AM﹣CN=MN;④M有可能是线段BE的中点.
A.1 B.2 C.3 D.4
7.已知:正方形ABCD中,对角线AC、BD相交于点O,∠DBC的角平分线BF交CD于点E,交AC于点F,OF=1,则AB=( )
A.2+ B.2﹣2 C.4﹣2 D.2+2
8.在四边形ABCD中,AB∥CD,AB=AD,添加下列条件不能推得四边形ABCD为菱形的是( )
A.AB=CD B.AD∥BC C.BC=CD D.AB=BC
9.如图,在正方形ABCD的外侧,作等边△ADE,则∠ABE为( )
A.10° B.15° C.20° D.25°
10.如图,正方形ABCD的边长为5,E是AD边上一点,AE=3,动点P由点D向点C运动,速度为每秒2个单位长度,EP的垂直平分线交AB于M,交CD于N.设运动时间为t秒,当PM∥BC时,t的值为( )
A. B.2 C. D.
11.如图,已知正方形ABCD中,AD=6,∠DAE=30°,点F为AE的中点,过点F作直线分别与AD、BC相交于点M、N,若MN=AE,则AM的长等于 .
12.如图,在矩形ABCD中,AB=3,AD=4.过点A作AG⊥BD于G,则BG等于 .
13.如图,坐标系中四边形ABCO是正方形,D是边OC上一点,E是正方形边上一点.已知B(﹣3,3),D(0,1),当AD=CE时,点E坐标为 .
14.如图,在正方形ABCD中,AB=2,点E为边BC中点,P为正方形边上一点,且PB=AE,则PE的长为 .
15.如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°,延长FC、AE交于点M,连接DF、BM,若C为FM中点,BM=5,则FD的长为 .
16.矩形一个角的角平分线分矩形一边为1和3两部分,则这个矩形的面积为 .
17.如图,在矩形AOBC中,点A的坐标是(﹣2,1),点C的纵坐标是4,则B点的纵坐标是 .
18.如图,在正方形ABCD中,点P为AD延长线上一点,连接AC、CP,F为AB边上点,满足CF⊥CP,AC=3,3DP=AB,则FP= .
19.已知矩形ABCD的对角线相交于点O,AE平分∠BAD交矩形的边于点E,若∠CAE=10°,则∠AOB的度数为 .
20.如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP= .
21.如图,在矩形ABCD中,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF;
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE的周长.
22.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.
(1)若∠B=30°,AC=6,求CE的长;
(2)过点F作AB的垂线,垂足为G,连接EG,试判断四边形CEGF的形状,并说明原因.
23.如图,正方形ABCD中,点E在BC边上,AF平分∠DAE,DF∥AE,AF与CD相交于点G.
(1)如图1,当∠AEC=120°,AE=4时,求FG的长;
(2)如图2,在AB边上截取点H,使得DH=AE,DH与AF、AE,分别交于点M、N,求证:AE=AH+DG.
24.如图①,正方形ABCD中,M是AB的中点,E是延长线上一点.MN⊥DM,且交∠CBE的平分线于N.
(1)若点F是AD的中点,求证:MD=MN;
(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任意一点”,其它条件不变.如图②所示,则结论“MD=MN”是否成立.若成立,给出证明;若不成立,请说明理由.
25.如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD,
(1)求证:AO=EO;
(2)当△ABC满足什么条件时四边形ABED是正方形?请说明理由.
26.在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
(1)如图1,若PB=a,AB=3a,求线段MN的长度;
(2)用等式表示ME、EF、NF之间的数量关系并证明.
27.如图,点G是正方形ABCD对角线CA的延长线一点,对角线BD与AC交于点O,以线段AG为边作一个正方形AEFG,连接EB、GD.
(1)求证:EB=GD;
(2)若AB=5,AG=2,求EB的长.
参考答案
1.解:∵四边形ABCD是正方形,
∴∠ABD=45°=∠ADB,
∵BE=BD,
∴∠BDE=67.5°,
∴∠EDA=∠BDE﹣∠ADB=22.5°,
故选:D.
2.解:如图,当点M在BC上时,
∵△ABM′和△DCE全等,
∴BM=CE,
由题意得:BM′=2t﹣4=3,
所以t=3.5(秒);
当点M在AD上时,
∵△ABM″和△CDE全等,
∴AM″=CE,
由题意得:AM″=16﹣2t=3,
解得t=6.5(秒).
所以,当t的值为3.5秒或6.5秒时.△ABM和△DCE全等.
故选:D.
3.解:A.因为矩形的对角线相等,所以A选项不符合题意;
B.因为矩形和菱形的对角线都互相平分,所以B选项不符合题意;
C.因为菱形对角线互相垂直,所以C选项符合题意;
D.因为矩形和菱形的对边都相等且平行,不符合题意.
故选:C.
4.解:∵四边形ABCD是矩形,
∴∠C=∠ABE=90°,AD∥BC,AB=CD,
∵DF=AB,
∴DF=CD,
∵DF⊥AE,
∴∠DFA=∠DFE=90°,
在Rt△DEF和Rt△DEC中,,
∴Rt△DEF≌Rt△DEC(HL),
∴∠FED=∠CED,
∴DE平分∠AEC;
故①正确;
∵AD∥BC,
∴∠AEB=∠DAF,
在△ABE和△AFD中,
,
∴△ABE≌△AFD(AAS),
∴AE=AD,
∴△ADE为等腰三角形;
故②正确;
∵△ABE≌△DFA,
∴不存在AF=AB,
故③错误;
∵△ABE≌△DFA,
∴BE=FA,
∴AE=AF+EF=BE+EF.
故④正确.
故正确的结论有①②④,三个.
故选:C.
5.解:如图,连接EF,
∵四边形ABCD为正方形,
∴∠EAO=∠FDO=45°,AO=DO;
∵∠EOF=90°,∠AOD=90°,
∴∠AOE=∠DOF;
在△AOE与△DOF中,
,
∴△AOE≌△DOF(ASA),
∴OE=OF(设为λ);
∴△EOF是等腰直角三角形,
由勾股定理得:
EF2=OE2+OF2=2λ2;
∴EF=OE=λ,
∵正方形ABCD的边长是4,
∴OA=2,O到AB的距离等于2(O到AB的垂线段的长度),
由题意可得:2≤λ≤2,
∴2≤EF≤4.
所以线段EF的最小值为2.
故选:D.
6.解:①∵四边形ABCD为正方形,
∴AB=BC,∠ABC=90°,
∴∠ABM+∠NBC=90°,
∵AM⊥BE于点M,CN⊥BE于点N,
∴∠AMB=∠BNC=90°,
∴∠ABM+∠BAM=90°,
∴∠NBC=∠BAM,
∴△ABM≌△BCN;
故①正确;
②∵∠BCE=∠CNE=90°,∠CEN=∠CEB,
∵CE≠BE,
∴△BCN∽△CEN,
故②不正确;
③∵△ABM≌△BCN,
∴AM=BN,BM=CN,
∴MN=BN﹣BM=AM﹣CN,
故③正确;
④当M是线段BE的中点时,E在点D处,而已知中E是边CD上(除端点外)任意一点,
所以M不可能是线段BE的中点.
故④不正确;
所以正确的有:①③2个,
故选:B.
7.解:如图,作FH∥BC交BD于点H.
∵四边形ABCD是正方形,
∴∠OBC=∠OCB=45°,OB=OC,∠BOC=90°
∵FH∥BC,
∴∠OHF=∠OBC,∠OFH=∠OCB,
∴∠OHF=∠OFH,
∴OH=OF=1,FH==,
∵BF平分∠OBC,
∴∠HBF=∠FBC=∠BFH,
∴BH=FH=,
∴OB=OC=1+,
∴AB=BC=OB=2+.
故选:A.
8.解:A选项:若AB=CD,∵AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
B选项:当AD∥BC时,又AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
C选项:当BC=CD时,△ABC≌△ACD(SAS),
∴∠A=∠C.
∵AB∥CD,
∴∠C+∠ABC=180°.
∴∠A+∠ABC=180°.
∴AD∥BC.
又AB∥CD,
∴四边形ABCD是平行四边形,
当AB=AD可判定四边形ABCD是菱形;
D选项只能说明四边形的三条边相等,所以不能判定是菱形.
故选:D.
9.解:∵四边形ABCD为正方形,△ADE为等边三角形,
∴AB=BC=CD=AD=AE=DE,∠BAD=90°,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,
又∵AB=AE,
∴∠ABE=(180°﹣150°)=15°.
故选:B.
10.解:如图,连接ME,
∵MN垂直平分PE,
∴MP=ME,
当MP∥BC时,四边形BCPM是矩形,
∴BC=MP=5,
∴ME=5,
又∵AE=3,
∴AM=4=DP,
∴t=4÷2=2(s),
故选:B.
11.解:在正方形ABCD中,AD=6,∠DAE=30°,
设DE=x,则AE=2x,由勾股定理x2+62=(2x)2,
解得:x=2(负值舍去),
∴AE=4,
∵点F为AE的中点,
∴AF=EF=2,
分两种情况:
①过M作MG⊥BC,G为垂足,则MG=DC=AD,
在Rt△MGN和Rt△ADE中,
,
∴Rt△MGN≌Rt△ADE(HL),
∴∠NMG=∠EAD,
∴∠NMG+∠AMF=90°,
∴∠EAD+∠AMF=90°,
∴∠AFM=90°,
在Rt△AFM中,∠DAE=30°,AF=2,
设MF=m,则AM=2m,
由勾股定理,得
4m2﹣m2=12,
解得m=2(负值舍去),则AM=4;
②如图,过N作NG⊥AD于G,过M作MH⊥AE于H,
则NG=CD=AD,
在Rt△ADE和Rt△NGM中,
,
∴Rt△ADE≌Rt△NGM(HL),
∴∠GNM=∠DAE=30°,
∴∠GMN=60°,
△AMF中,∠GMN=∠MAF+∠AFM,
∴∠AFM=∠DAE=30°,
∴AM=MF,
∵MH⊥AF,
∴AH=FH,
设MH=x,则AM=2x,AH=FH=x,
∵F是AE的中点,
∴AE=2AF=4AH=4x,
Rt△ADE中,∠DAE=30°,
∴DE=AE=2x,AD=DE=6x,
∵AD=6,即6x=6,
x=1,即AM=2x=2;
故答案为:4或2.
12.解:∵四边形ABCD是矩形,
∴∠BAD=90°,
∴BD===5,
由三角形的面积公式得,BD?AG=AB?AD,
∴AG===,
∴BG===,
故答案为:.
13.解:如图,符合条件的点有两个,当点E在边AB和边OA上时,设为点E′和点E″,
∵B(﹣3,3),D(0,1),
∴AB=OA=3,OD=1,
∵四边形ABCO是正方形,
∴AB=BC=OC=OA=3,∠B=∠AOD=90°,
∵AD=CE′=CE″,
在Rt△BCE′和Rt△OAD中,
,
∴Rt△BCE′≌Rt△OAD(HL),
∴BE′=OD=1,
∴AE′=AB﹣BE′=2,
∴E′(﹣3,2);
同理Rt△OCE′≌Rt△OAD(HL),
∴OE″=OD=1,
∴E′(﹣1,0).
所以点E坐标为(﹣3,2)或(﹣1,0).
故答案为:(﹣3,2)或(﹣1,0).
14.解:当点P在AD边上时,
∵PB=AE,点E为边BC中点,
∴点P为边AD中点,
∴PE=AB=2;
当点P在CD边上时,
∵PB=AE,点E为边BC中点,
∴点P为边CD中点,
∴PE===.
所以PE的长为:2或.
故答案为:2或.
15.解:如图,过C点作CH⊥BF于H点,过B点作BK⊥CM于K,过D作DQ⊥MF交MF延长线于Q.
∵∠CFB=45°
∴CH=HF,
∵∠ABG+∠BAG=90°,∠FBE+∠ABG=90°,
∴∠BAG=∠FBE,
∵AG⊥BF,CH⊥BF,
∴∠AGB=∠BHC=90°,
在△AGB和△BHC中,
∵∠AGB=∠BHC,∠BAG=∠HBC,AB=BC,
∴△AGB≌△BHC(AAS),
∴AG=BH,BG=CH,
∵BH=BG+GH,
∴BH=HF+GH=FG,
∴AG=FG;
∵CH⊥GF,
∴CH∥GM,
∵C为FM的中点,
∴CH=GM,
∴BG=GM,
∵BM=5,
∴BG=,GM=2,
∴AG=2,AB=5,
∴HF=,
∴CF=×=,
∴CM=,
∵CK=CM=CF=,
∴BK=,
∵在△BKC和△CQD中,
∵∠CBK=∠DCQ,∠BKC=∠CQD=90°,BC=CD,
∴△BKC≌△CQD(AAS),
∴CQ=BK=,
DQ=CK=,
∴QF=CQ﹣CF=﹣=,
∴DQ=QF=,
∴DF=×=.
故答案为.
16.解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠AEB=∠ABE,
∴AB=AE,
①如图,当AE=3时,AB=3,AD=1+3=4,
此时矩形的面积是:3×4=12;
②同理可得,当AE=1时,AB=1,AD=4,
此时矩形的面积是1×4=4;
故答案为:4或12.
17.解:如图,
过点A作AD⊥x轴于点D,
过点B作BE⊥x轴于点E,
过点C作CF∥y轴,过点A作AF∥x轴,交点为F,
则AF⊥CF,
延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴OB=AC,AC∥OB,
∴∠CAF=∠CHO=∠BOE,
∵∠AFC=∠OEB=90°,
∴△AFC≌△OEB(AAS),
∴CF=BE=4﹣1=3,
故答案为:3.
18.解:∵四边形ABCD是正方形,
∴AB=CB=CD=AD,
∠CBF=∠CDP=∠BCF+∠FCD=90°,
又∵CF⊥CP,
∴∠DCP+∠FCD=90°,
∴∠BCF=∠DCP,
在△BCF和△DCP中,
∴△BCF≌△DCP(AAS),
∴BF=DP,
∵AC=3,∠ABC=90°,AB=BC,
∴2AB2=AC2=32=9
∴AB=,
∴AD=,
∵3DP=AB,
∴DP=,
∴BF=DP=,
∴AF=AB﹣BF=﹣=,
AP=AD+DP=+=2,
在Rt△AFP中,
FP===.
故答案为:.
19.解:由题得,画出如下示意图:
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OB=OD,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∵∠CAE=10°,
由图(1)得:∠BAO=∠BAE+∠EAC=45°+10°=55°,
又∵OA=OB,
∴∠BAO=∠OBA=55°,
∴∠AOB=180°﹣55°﹣55°=70°,
由图(2)得:∠DAO=∠DAE+∠EAC=45°+10°=55°,
又∵OA=OD,
∴∠OAD=∠ODA=55°,
∴∠AOB=∠OAD+∠ODA=110°,
综上所述:∠AOB的值为:70°、110°,
故答案为:70°、110°.
20.解:∵矩形ABCD中,AB=4,AD=3=BC,
∴Rt△ACD中,AC==5,
又∵AQ=AD=3,AD∥CP,
∴CQ=5﹣3=2,∠CQP=∠AQD=∠ADQ=∠CPQ,
∴CP=CQ=2,
∴BP=3﹣2=1,
∴Rt△ABP中,AP===,
故答案为:.
21.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,DO=BO,
∴∠EDO=∠FBO,
又∵EF⊥BD,
∴∠EOD=∠FOB=90°,
在△DOE和△BOF中,
,
∴△DOE≌△BOF(ASA);
(2)解:∵由(1)可得,ED∥BF,ED=BF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形,
根据AB=6,AD=8,设AE=x,可得BE=ED=8﹣x,
在Rt△ABE中,根据勾股定理可得:BE2=AB2+AE2,
即(8﹣x)2=x2+62,
解得:,
∴,
∴四边形BFDE的周长=.
22.解:(1)∵∠ACB=90°,∠B=30°,
∴∠CAB=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
∵AF平分∠CAB,
∴∠CAF=∠BAF=30°,
∴CE=AE,
过点E用EH垂直于AC于点H,
∴CH=AH
∵AC=6,
∴CE=2
答:CE的长为2;
(2)∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF,
在Rt△ACF与Rt△AGF中,
AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),
∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,
∴CD∥FG,
∴∠CEF=∠EFG,
∴∠CEF=∠CFE,
∴CE=CF,
∴CE=FG,
∴四边形CEGF是菱形
23.解:(1)∵∠AEC=120°,
∴∠AEB=180°﹣120°=60°,
∵四边形ABCD是正方形,
∴∠B=∠BAD=∠ADC=90°,AD∥BC,
∴∠BAE=30°,∠DAE=∠AEB=60°,
∵AF平分∠DAE,
∴∠DAF=∠EAF=30°,
Rt△ABE中,AE=4,∠BAE=30°,
∴BE=2,AB=AD=2,
Rt△ADG中,∠DAG=30°,
∴DG=2,
∵DF∥AE,
∴∠F=∠EAF=30°,
∵∠AGD=60°,
∴∠GDF=∠F=30°,
∴GF=DG=2;
(2)由(1)知:∠F=∠DAF,
∴AD=DF,
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=90°,
∵AE=DH,
∴Rt△DAH≌Rt△ABE(HL),
∴∠BAE=∠ADH,
∵∠BAE+∠DAE=∠ADH+∠DAE=90°,
∴∠AND=90°,
∵DF∥AE,
∴∠HDF=∠HNE=90°,
∴∠MDG+∠GDF=∠ADM+∠MDG=90°,
∴∠ADM=∠GDF,
∴△ADM≌△FDG(ASA),
∴DM=DG,
∴∠DMG=∠DGM,
∵AH∥DG,
∴∠HAM=∠DGM,
∵∠AMH=∠DMG,
∴∠HAM=∠AMH,
∴AH=HM,
∴DH=HM+DM=AH+DG=AE.
24.解:(1)如图,取AD的中点F,连接FM.
∵∠FDM+∠DMA=∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∵AF=AD=AB=AM=MB=DF,
∵BN平分∠CBE,即∠NBE=∠CBE=45°,
又∵AM=AF,
∴∠AFM=45°,
∴∠DFM=∠MBN=135°.
∵DF=MB,
在△DFM和△MBN中
,
∴△DFM≌△MBN(ASA).
∴DM=MN.
(2)结论“DM=MN”仍成立.
证明如下:如图,在AD上截取AF'=AM,连接F'M.
∵DF'=AD﹣AF',MB=AB﹣AM,AD=AB,AF'=AM,
∴DF'=MB.
∵∠F'DM+∠DMA=∠BMN+∠DMA=90°,
∴∠F'DM=∠BMN.
又∠DF'M=∠MBN=135°,
在△DF'M和△MBN中
,
∴△DF'M≌△MBN(ASA).
∴DM=MN.
25.解:(1)证明:∵AD∥BC,
∴∠CBD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
又∵AE⊥BD,
∴BO=DO,
又∵∠AOD=∠EOB,
∴△AOD≌△EOB,
∴AO=EO;
(2)当△ABC满足∠ABC=90°时,四边形AECD是正方形.理由:
∵△AOD≌△EOB,
∴AD=BE,
又∵AD∥BE,AE⊥BD,
∴四边形ABED是菱形,
∴当∠ABC=90°时,菱形ABED是正方形,
即当△ABC满足∠ABC=90°时,四边形AECD是正方形.
26.解:(1)如图所示,过N作NG⊥AB,交AB于点G. 则四边形AGND是矩形,所以NG=AD=AB=3a,
∵MN⊥AP∴∠MNG=∠PAB 且∠PBA=∠NGMAB=NG∴△ABP≌△NGM
∴MN=AP==
(2)如图所示,过P作PH∥AB,过F作ST∥AB,连接AF,PF
∵NM垂直平分AP,则AE=PE,∠AEM=∠PEH=90°,
∵PH∥AB∴∠PHE=∠MEA,∠HPE=∠MAE
∴△AME≌△PHE
∴ME=HE
∠TDF=∠FBP=45°
∴TD=TF,FS=BS
∵BS=AT=FS
∵点F在线段AP的垂直平分线上,
∴FP=FA
∴Rt△FPS≌Rt△ATF
∴PS=TF=TD=SC=PS
∵PH∥TS∥CD
∴HF=FN
∴ME+NF=EF
27.(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD,
∴∠GAD=∠EAB,
在△GAD和△EAB中,
∴△GAD≌△EAB,
∴EB=GD;
(2)∵四边形ABCD是正方形,AB=5,
∴BD⊥AC,AC=BD=5,
∴∠DOG=90°,OA=OD=BD=,
∵AG=2,
∴OG=OA+AG=,
由勾股定理得,GD==,
∴EB=.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
