9.4矩形、菱形、正方形尖子生训练卷(Word版 含解析)
文档属性
| 名称 | 9.4矩形、菱形、正方形尖子生训练卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 611.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-27 00:00:00 | ||
图片预览



文档简介
9.4矩形、菱形、正方形尖子生训练卷
1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
2.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A. B. C. D.
3.如图,正方形ABCD的面积为16cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长( )
A.4cm B.6cm C.8cm D.10cm
4.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则OE的长度是( )
A. B.5 C.3 D.
5.如图,在正方形ABCD中,点E是CD的中点,点F是AD的中点,BE与CF相交于点P,设AB=a.得到以下结论:
①BE⊥CF;②AP=a;③CP=a
则上述结论正确的是( )
A.①② B.①③ C.②③ D.①②③
6.如图,AB⊥AF,EF⊥AF,BE与AF交于点C,点D是BC的中点,∠AEB=2∠B.若BC=8,EF=,则AF的长是( )
A. B. C.3 D.5
7.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )
A.3 B.2 C. D.4
8.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,
④CF=BD=2,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
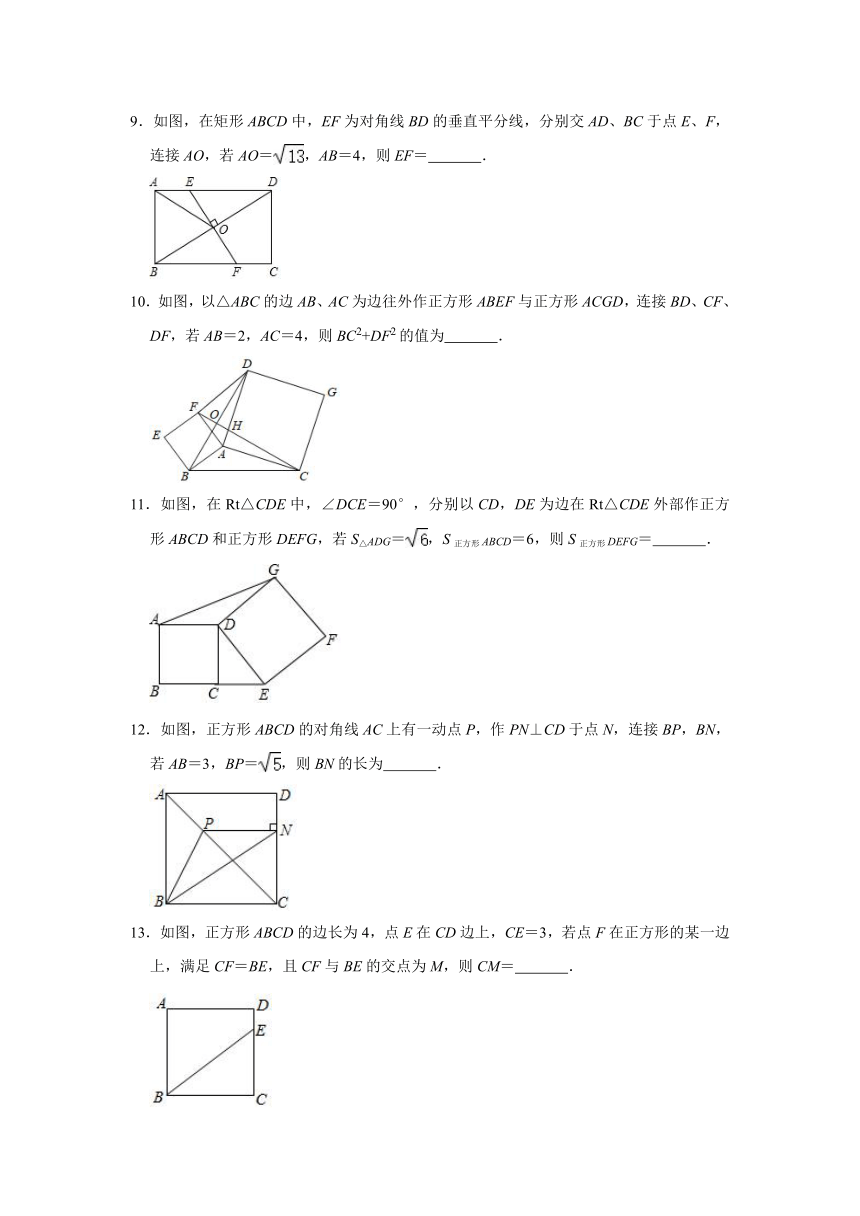
9.如图,在矩形ABCD中,EF为对角线BD的垂直平分线,分别交AD、BC于点E、F,连接AO,若AO=,AB=4,则EF= .
10.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC=4,则BC2+DF2的值为 .
11.如图,在Rt△CDE中,∠DCE=90°,分别以CD,DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,若S△ADG=,S正方形ABCD=6,则S正方形DEFG= .
12.如图,正方形ABCD的对角线AC上有一动点P,作PN⊥CD于点N,连接BP,BN,若AB=3,BP=,则BN的长为 .
13.如图,正方形ABCD的边长为4,点E在CD边上,CE=3,若点F在正方形的某一边上,满足CF=BE,且CF与BE的交点为M,则CM= .
14.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 .
15.如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,当点F是CD的中点时,若AB=4,则BC= .
16.如图,四边形ABCD是正方形,△CDE是等边三角形,则∠AEB= .
17.如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为 .
18.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②△ABE≌△AHD;③BH=FH;④AB=HF;⑤BC﹣CF=2HE.其中正确的有
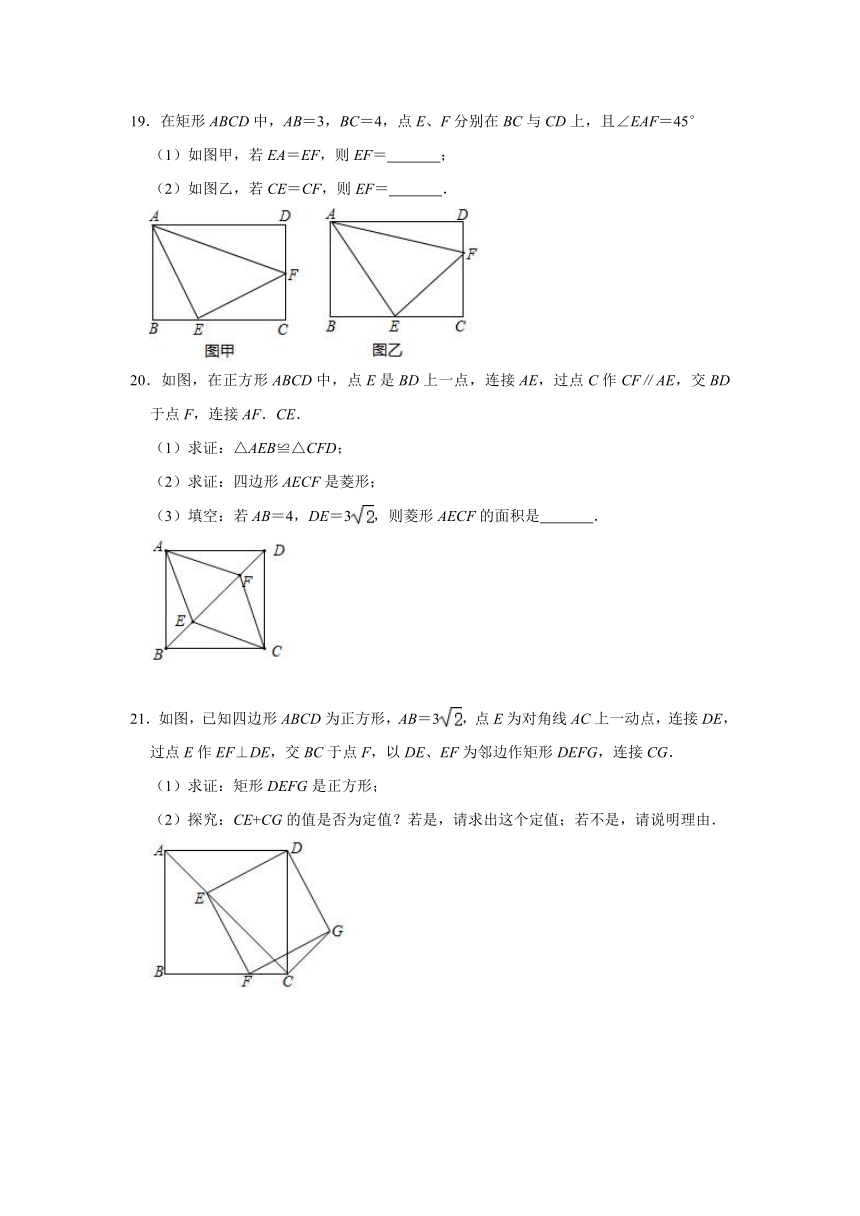
19.在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°
(1)如图甲,若EA=EF,则EF= ;
(2)如图乙,若CE=CF,则EF= .
20.如图,在正方形ABCD中,点E是BD上一点,连接AE,过点C作CF∥AE,交BD于点F,连接AF.CE.
(1)求证:△AEB≌△CFD;
(2)求证:四边形AECF是菱形;
(3)填空:若AB=4,DE=3,则菱形AECF的面积是 .
21.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
22.如图,在菱形ABCD中,∠A=60°,AB=4,E是AD边上的动点,作∠BEF=60°交CD于点F,在AB上取点G使AG=AE,连接EG.
(1)求∠EGB的度数;
(2)求证:EF=BE;
(3)若P是EF的中点,当AE为何值时,△EGP是等腰三角形.
23.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)AF垂直平分线线段BO于点F,AC=12,求BC的长.
24.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,AE=AD,作DF⊥AE于点F.
(1)求证:AB=AF;
(2)连BF并延长交DE于G.
①求证:EG=DG;
②若EG=1,求矩形ABCD的面积.
25.如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,点E,F分别是垂足.
(1)求证:AP=PC;
(2)若∠BAP=60°,PD=,求PC的长.
26.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
参考答案
1.解:①由矩形的判定“对角线相等的平行四边形是矩形”可知,A正确;
②由菱形的判定“有一组邻边相等的平行四边形是菱形”可知,B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④在平行四边形ABCD中,
∵∠DAB=90°,
∴平行四边形ABCD是矩形,而不能判定其是正方形,故D错误;
故选:D.
2.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
3.解:延长CB至M,使BM=DH,连接AM;如图所示:
∵四边形ABCD是正方形,正方形ABCD的面积为16cm2,
∴AB=BC=CD=4cm,∠BAD=∠ABC=∠D=90°,
∴∠ABM=90°,
在△ABM和△ADH中,
,
∴△ABM≌△ADH(SAS),
∴AM=AH,∠BAM=∠DAH,
∵△AEF是等腰直角三角形,
∴∠HAG=45°,
∴∠BAG+∠DAH=45°,
∴∠MAG=45°,
在△AMG和△AHG中,
,
∴△AMG≌△AHG(SAS),
∴GM=GH,
∴△CGH的周长=GH+CG+CH=GM+CG+CH
=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=8.
故选:C.
4.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=10,OA=OC=AC=5,OB=OD=BD=5,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°﹣∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∴∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴(2DE)2=OD2=25,
∴DE=,
故选:D.
5.解:在△CDF和△BCE中
∴△CDF≌△BCE(SAS)
∴∠CEB=∠CFD
∵∠DCF+∠CFD=90°
∴∠DCF+∠CEB=90°
∴∠EPC=90°
∴①正确;
如图延长CF交BA延长线于点M,
在△CFD和△MFA中
∴△CFD≌△MFA(ASA)
∴CD=MA=AB=a,
∵BP⊥CF
∴AP为Rt△MPB斜边BM上的中线,是斜边的一半,即AP=BM=×2a=a,
∴②正确;
∵CP⊥BE
∴CP×BE=CE×BC=
∵BE===
∴CP===
∴③正确
故选:D.
6.解:∵AB⊥AF,
∴∠FAB=90°,
∵点D是BC的中点,
∴AD=BD=BC,
∴∠DAB=∠B,
∴∠ADE=∠B+∠BAD=2∠B,
∵∠AEB=2∠B,
∴∠AED=∠ADE,
∴AE=AD,
∵BC=8,
∴AE=AD=4,
∵EF=,EF⊥AF,
∴AF===3,
故选:C.
7.解:
连接OB,过B作BM⊥x轴于M,
∵点B的坐标是(1,3),
∴OM=1,BM=3,由勾股定理得:OB==,
∵四边形OABC是矩形,
∴AC=OB,
∴AC=,
故选:C.
8.解:①∵EF=2,
∴OE=4,
∵AO=AB=6,
∴AE=AO+OE=6+4=10,故正确;
②∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;
③作FG⊥CO交CO的延长线于G,
则FG=2,
∴△COF的面积S△COF=×6×2=6,故正确;
④作DH⊥AB于H,
CF==2,
BH=6﹣2=4,
DH=6+2=8,
BD==4,故错误.
故选:A.
9.解:连接DF,
∵EF为矩形ABCD的对角线BD的垂直平分线,AO=,
∴BD=2DO=2AO=,BF=DF,∠DOF=90°,
∴DO=,
在矩形ABCD中,∠C=90°,CD=AB=4,AD∥BC,
∴BD2=BC2+CD2,
即,
解得BC=6,
∵DF2=CF2+CD2,
∴DF2=(6﹣DF)2+42,
解得DF=,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=∠DOF=90°,
∵AD∥BC,
∴∠EDO=∠FBO,
∴△EDO≌△FBO(ASA),
∴OE=OF=EF,
在Rt△DOF中,DF2=OF2+OD2,
∴OF2+()2=()2,
解得OF=,
∴EF=.
故答案为.
10.解:如图所示,连接BF,CD,
∵四边形ABEF,四边形ACGD都是正方形,
∴AB=AF,AC=AD,∠BAF=∠CAD=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS),
∴∠ACF=∠ADB,
又∵∠AHC=∠OHD,
∴∠CAH=∠DOH=90°,
∴CF⊥BD,
∴BC2=OB2+OC2,DF2=OD2+OF2,BF2=OB2+OF2,DC2=OD2+OC2,
∴BC2+DF2=OD2+OF2+OB2+OC2,
BF2+DC2=OD2+OF2+OB2+OC2,
即BC2+DF2=BF2+DC2,
又∵△ABF和△ACD都是等腰直角三角形,且AB=2,AC=4,
∴BF2+DC2=8+32=40,
∴BC2+DF2=40,
故答案为:40.
11.解:如图所示,过G作GH⊥AD,交AD的延长线于H,则∠H=90°,
又∵∠DCE=90°,
∴∠H=∠DCE,
∵四边形ABCD和四边形DEFG是正方形,
∴∠ADC=∠CDH=∠EDG=90°,DG=DE,
∴∠GDH=∠EDC,
∴△DGH≌△DEC(AAS),
∴GH=CE,
∵S正方形ABCD=6,
∴CD=,
∵S△ADG=,
∴AD×GH=,
又∵AD=CD,
∴CD×CE=,即×CE=,
∴CE=2,
∴Rt△CDE中,DE===,
∴S正方形DEFG=DE2=10,
故答案为:10.
12.解:延长NP交AB于H,
∵四边形ABCD为正方形,
∴∠BAC=90°,AB∥CD,
∵PN⊥CD,
∴PN⊥AB,
∴∠HAP=∠HPA=45°,
∴AH=PH,
设AH=PH=x,则BH=3﹣x,
在Rt△PBH中,PB2=PH2+BH2,
∴,
解得x=1或2,
当x=1时,BH=CN=2,在Rt△BCN中,;
当x=2时,BH=CN=1,在Rt△BCN中,.
故答案为或.
13.解:分两种情况:
①如图1所示,当点F在AD上时,
由CF=BE,CD=BC,∠BCE=∠CDF=90°可得,Rt△BCE≌Rt△CDF(HL),
∴∠DCF=∠CBE,
又∵∠BCF+∠DCF=90°,
∴∠BCF+∠CBE=90°,
∴∠BMC=90°,即CF⊥BE,
∵BC=4,CE=3,∠BCE=90°,
∴BE=5,
∴CM==;
②如图2所示,当点F在AB上时,
同理可得,Rt△BCF≌Rt△CBE(HL),
∴BF=CE,
又∵BF∥CE,
∴四边形BCEF是平行四边形,
又∵∠BCE=90°,
∴四边形BCEF是矩形,
∴CM=BE=×5=.
故答案为:或.
14.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故答案为16
15.解:如图,连接BF,作FH⊥BE于H.作FM∥BE交BC于M.
∵四边形ABCD是矩形,
∴AB=CD=4,∠D=∠C=∠ABC=90°,
∵F是CD中点,
∴DF=FC=2,
∵EF平分∠BED,FH⊥EB,FD⊥ED,
∴FH=FD=FC,
∵BF=BF,
∴Rt△BFH≌Rt△BFC,
∴∠FBC=∠FBE,
∵BE平分∠ABC,
∴∠ABE=45°,
∴∠FBC=∠FBH=22.5°,
∵FM∥BE,
∴∠FMC=∠EBC=45°,
∵∠FMC=∠FBM+∠MFB,
∴∠MFB=∠MBF=22.5°,
∴FM=BM,
∵∠FMC=∠CFM=45°,CF=2,
∴FM=BM=2,
∴BC=BM+CM=2+2.
故答案为2+2.
16.解:∵四边形ABCD是正方形,△CDE是等边三角形,
∴AD=CD=DE;∠ADE=90°+60°=150°,
∴∠AED=(180°﹣150°)÷2=15°.
同理可得∠CEB=15°,
∴∠AEB=∠DEC﹣∠DEA﹣∠CEB=30°.
故答案为:30°.
17.解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=AC,
∴四边形BGFD是菱形,
∴GF=BG=5,则AF=13﹣5=8,AC=2×5=10,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即82+CF2=102,
解得:CF=6.
故答案是:6.
18.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=90°,AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴∠BAE=∠DAH=45°,
∴△ABE和△ADH是等腰直角三角形,
∴AE=AB,AD=AH,
∵AD=AB=AH,
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
在△ABE和△AHD中,,
∴△ABE≌△AHD(AAS),故②正确;
∴BE=DH,
∵AB=AH,
∵∠AHB=(180°﹣45°)=67.5°,
∴∠OHE=∠AHB=67.5°,
∴∠DHO=90°﹣67.5°=22.5°,
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,,
∴△BEH≌△HDF(ASA),
∴BH=HF,故③正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故④错误;
过H作HK⊥BC于K,
可知KC=BC,HK=KE,
由上知HE=EC,
∴BC=KE十EC,
又KE=HK=FC,HE=EC,
故BC=HK+HE,BC=2HK+2HE=FC+2HE
∴⑤正确;
故答案为:①②③⑤.
19.解:(1)如图甲所示:
∵EA=EF,
∴△AEF是等腰直角形,∠EAF=∠EFA,
∵∠EAF=45°,
∴∠EFA=45°,
又∵在△AEF中,∠EAF+∠EFA+∠AEF=180°,
∴∠AEF=180°﹣45°﹣45°=90°,
又∵∠AEB+∠AEF+∠FEC=180°,
∴∠AEB+∠FEC=90°,
又∵△ABE中,∠B+∠BAE+∠AEB=180°,
∠B=90°,
∴∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
在△ABE和△ECF中
,
∴△ABE≌△ECF(AAS)
∴AB=EC,BE=CF,
又∵AB=3,BC=4,
∴EC=3,CF=1,
在Rt△CEF中,由勾股定理得:
==
故答案为.
(2)如图乙所示:
作DM=DF,BN=BE,分别交AD,AB于点M和点N,设MD=x,
∵四边形ABCDA是矩形,
∴∠B=∠D=90°,
∴∠BNE=45°,∠DMF=90°,
又∵∠BNE+∠ENA=180°,∠FMD+∠FMA=180°,
∴∠ENA=135°,∠FMA=135°,
又∵∠EAF=45°,∠BAD=∠BAE+∠EAF+∠FAD=90°,
∴∠BAE+∠FAD=45°,
∵∠BAE+∠NEA=45°,
在△ANE和△FMA中
,
∴△ANE∽△FMA(AA)
∴;
又∵MD=x,∴DF=x,
∵CE=CF,AB=3,BC=4,
∴FC=EC=3﹣x,BE=AB=x+1,AN=2﹣x,
∴,
解得:2﹣4,或﹣2﹣4(舍去),
∴FC=3﹣()=7﹣2,
∴EF=FC=(7﹣2)=7﹣4.
故答案为7﹣4.
20.解:连接AC交BD于点O,如图所示:
(1)∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABE=∠CBE=∠CDF,
又∵CF∥AE,
∴∠AEF=∠CFE,
又∵∠AEF+∠AEB=180°,∠CFE+∠CFD=180°,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
,
∴△AEB≌△CFD(AAS);
(2)∵△AEB≌△CFD,
∴AE=CF,
∴四边形AECF是平行四边形,
在△ABE和△CBE中
,
∴△ABE≌△CBE(SAS)
∴AE=EC,
∴?AECF是菱形;
(3)∵AB=4,AB=BC=CD,
∴在Rt△BCD中,由勾股定理得,
BD===,
又∵BD=BE+ED,DE=3,
∴BE=
又∵BE=DF,
∴DF=,EF=,
又∵AC=BD,
∴AC=4,
∴==8
故答案为8.
21.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
22.(1)解:∵∠A=60°,AG=AE,
∴△AGE是等边三角形,
∴∠AGE=60°,
∴∠EGB=120°;
(2)证明:由(1)知,∠EGB=120°,
∵四边形ABCD为菱形,
∴AB∥CD,AB=AD,
∴∠A+∠D=180°,
∵∠A=60°,
∴∠D=120°,
∴∠DEF+∠DFE=60°,
∴∠D=∠EGB,
∵△AGE是等边三角形,
∴AE=AG,∠AEG=60°,
∴DE=GB,
∵∠BEF=60°,
∴∠DEF+∠GEB=60°,
∴∠DFE=∠GEB,
∴△DFE≌△GEB(ASA),
∴EF=BE;
(3)解:∵△DFE≌△GEB,
∴DF=GE,
当EG=EP时,过E作EM⊥AB 垂足为M,
设AE=x,
∵△AGE是等边三角形,
∴AM=x,EM=x,
∴BM=4﹣x,
∵P为EF的中点,
∴EF=2EP,
由(2)知EF=BE,
∴EB=2EG=2AE=2x,
在Rt△EBM中,EM2+BM2=EB2,
即(x)2+(4﹣x)2=(2x)2,
解得,(舍去),
即AE=;
当EG=GP时,过G作GQ⊥EF,垂足为Q,过B作BH⊥CD垂足为H,连接BF,设AE=x,
∵△AGE是等边三角形,
∴EG=x,
∵EF=EB,∠BEF=60°,
∴△BEF为等边三角形,
∴∠EFB=∠BEF=60°,EF=BF,
∵△BEG≌△EFD,
∴∠BEG=∠EFD,DF=EG,
∴∠GEQ=∠BFH,CF=4﹣x,
∵∠EQG=∠FHB=90°,
∴△EGQ∽△FBH,
∴EG:BF=EQ:FH,
设△BEF的边长为a,
则BF=EF=a,
∵P为EF的中点,
∴EP=a,
∵EG=GP=x,
∴EQ=EP=a,
在Rt△BCH中,BC=AB=4,∠C=∠A=60°,
∴CH=2,
∴BH=,
∴HF=2﹣(4﹣x)=x﹣2,
∵BF2=BH2+HF2,
∴a2=()2+(x﹣2)2,
∵EG:BF=EQ:FH,
∴,
即a2=4x2﹣8x,
∴
解得,(舍去),
即AE=;
当EP=GP时,点P在EG的中垂线上,即P点AC上,
而运动期间P不可能位于线段AC上,
∴P在AC上不存在,
综上,AE=或;
即当AE为或时,△EGP是等腰三角形.
23.证明:(1)∵DE∥AC,CE∥BD,
∴四边形DOCE是平行四边形,
∵矩形ABCD的对角线AC,BD相交于点O,
∴AO=CO=DO=BO,
∴四边形OCED为菱形.
(2)过O作OE⊥BC,
∵矩形ABCD的对角线AC、BD相交于点O,
∴OA=OB,
∵AF垂直平分线线段BO于点F,
∴AB=AO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∴∠BOC=120°,
∴∠BOE=60°,
∴∠OBE=30°,∠OEB=90°,
∴BE=,
∴BC=6.
24.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,∠DAB=∠ABE=90°,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠BAE=∠AEB=45°,
∴AB=EB,
∵DF⊥AC
∴∠AFD=90°,
∴∠ABE=∠AFD=90°,
∵AE=AD,
∴△ABE≌△AFD(AAS),
∴AB=AF;
(2)①证明:∵AE=AD,∠EAD=45°,
∴∠AED=∠ADE=67.5°,
∴∠FDG=22.5°,
∵AB=AF,∠BAF=45°,
∴∠AFB=67.5°,
∴∠EFG=67.5°,
∴∠EFG=∠AED,
∴FG=EG,∠DFG=22.5°,
∴∠DFG=∠FDG,
∴FG=DG,
∴EG=DG;
②解:∵EG=1,
∴ED=2,
设AB=x,则AE=,DF=AF=x,
∴EF=﹣x,
∴(﹣x)2+x2=22,
解得x2=,
∴矩形ABCD的面积==.
25.(1)证明:∵ABCD是正方形,
∴∠C=90°,
∵PE⊥CD,PF⊥BC,
∴四边形PFCE是矩形,
∴EF=PC,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴AP=CP;
(2)解:∵由(1)知△ABP≌△CBP,
∴∠BAP=∠BCP=60°,
∴∠PCE=30°,
∵四边形ABCD是正方形,BD是对角线,
∴∠PDE=45°,
∵PE⊥CD,
∴DE=PE,
∵PD=,
∴PE=1,
∴PC=2PE=2.
26.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
1.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC平分∠BAD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
2.已知:如图,矩形ABCD中,AB=5,BC=12,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥BD于点E,PF⊥AC于点F,则PE+PF等于( )
A. B. C. D.
3.如图,正方形ABCD的面积为16cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长( )
A.4cm B.6cm C.8cm D.10cm
4.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则OE的长度是( )
A. B.5 C.3 D.
5.如图,在正方形ABCD中,点E是CD的中点,点F是AD的中点,BE与CF相交于点P,设AB=a.得到以下结论:
①BE⊥CF;②AP=a;③CP=a
则上述结论正确的是( )
A.①② B.①③ C.②③ D.①②③
6.如图,AB⊥AF,EF⊥AF,BE与AF交于点C,点D是BC的中点,∠AEB=2∠B.若BC=8,EF=,则AF的长是( )
A. B. C.3 D.5
7.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是( )
A.3 B.2 C. D.4
8.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,
④CF=BD=2,其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
9.如图,在矩形ABCD中,EF为对角线BD的垂直平分线,分别交AD、BC于点E、F,连接AO,若AO=,AB=4,则EF= .
10.如图,以△ABC的边AB、AC为边往外作正方形ABEF与正方形ACGD,连接BD、CF、DF,若AB=2,AC=4,则BC2+DF2的值为 .
11.如图,在Rt△CDE中,∠DCE=90°,分别以CD,DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,若S△ADG=,S正方形ABCD=6,则S正方形DEFG= .
12.如图,正方形ABCD的对角线AC上有一动点P,作PN⊥CD于点N,连接BP,BN,若AB=3,BP=,则BN的长为 .
13.如图,正方形ABCD的边长为4,点E在CD边上,CE=3,若点F在正方形的某一边上,满足CF=BE,且CF与BE的交点为M,则CM= .
14.如图,点P是矩形ABCD的对角线AC上一点,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若AE=2,PF=8.则图中阴影部分的面积为 .
15.如图,在矩形ABCD中,∠B的平分线BE与AD交于点E,∠BED的平分线EF与DC交于点F,当点F是CD的中点时,若AB=4,则BC= .
16.如图,四边形ABCD是正方形,△CDE是等边三角形,则∠AEB= .
17.如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为 .
18.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②△ABE≌△AHD;③BH=FH;④AB=HF;⑤BC﹣CF=2HE.其中正确的有
19.在矩形ABCD中,AB=3,BC=4,点E、F分别在BC与CD上,且∠EAF=45°
(1)如图甲,若EA=EF,则EF= ;
(2)如图乙,若CE=CF,则EF= .
20.如图,在正方形ABCD中,点E是BD上一点,连接AE,过点C作CF∥AE,交BD于点F,连接AF.CE.
(1)求证:△AEB≌△CFD;
(2)求证:四边形AECF是菱形;
(3)填空:若AB=4,DE=3,则菱形AECF的面积是 .
21.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
22.如图,在菱形ABCD中,∠A=60°,AB=4,E是AD边上的动点,作∠BEF=60°交CD于点F,在AB上取点G使AG=AE,连接EG.
(1)求∠EGB的度数;
(2)求证:EF=BE;
(3)若P是EF的中点,当AE为何值时,△EGP是等腰三角形.
23.如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)AF垂直平分线线段BO于点F,AC=12,求BC的长.
24.如图,在矩形ABCD中,∠BAD的平分线交BC于点E,AE=AD,作DF⊥AE于点F.
(1)求证:AB=AF;
(2)连BF并延长交DE于G.
①求证:EG=DG;
②若EG=1,求矩形ABCD的面积.
25.如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,点E,F分别是垂足.
(1)求证:AP=PC;
(2)若∠BAP=60°,PD=,求PC的长.
26.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG,如图1所示.
(1)证明平行四边形ECFG是菱形;
(2)若∠ABC=120°,连接BG、CG、DG,如图2所示,
①求证:△DGC≌△BGE;
②求∠BDG的度数;
(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,如图3所示,求DM的长.
参考答案
1.解:①由矩形的判定“对角线相等的平行四边形是矩形”可知,A正确;
②由菱形的判定“有一组邻边相等的平行四边形是菱形”可知,B正确;
③∵AC平分∠BAD,
∴∠DAC=∠CAB,
∵CD∥AB,
∴∠DCA=∠CAB,
∴∠DAC=∠DCA,
∴DA=DC,
∴平行四边形ABCD是菱形,故C正确;
④在平行四边形ABCD中,
∵∠DAB=90°,
∴平行四边形ABCD是矩形,而不能判定其是正方形,故D错误;
故选:D.
2.解:连接PO,
∵矩形ABCD的两边AB=5,BC=12,
∴S矩形ABCD=AB?BC=60,OA=OC,OB=OD,AC=BD,AC===13,
∴S△AOD=S矩形ABCD=15,OA=OD=AC=,
∴S△AOD=S△AOP+S△DOP=OA?PE+OD?PF=OA(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故选:C.
3.解:延长CB至M,使BM=DH,连接AM;如图所示:
∵四边形ABCD是正方形,正方形ABCD的面积为16cm2,
∴AB=BC=CD=4cm,∠BAD=∠ABC=∠D=90°,
∴∠ABM=90°,
在△ABM和△ADH中,
,
∴△ABM≌△ADH(SAS),
∴AM=AH,∠BAM=∠DAH,
∵△AEF是等腰直角三角形,
∴∠HAG=45°,
∴∠BAG+∠DAH=45°,
∴∠MAG=45°,
在△AMG和△AHG中,
,
∴△AMG≌△AHG(SAS),
∴GM=GH,
∴△CGH的周长=GH+CG+CH=GM+CG+CH
=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=8.
故选:C.
4.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=10,OA=OC=AC=5,OB=OD=BD=5,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°﹣∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∴∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴(2DE)2=OD2=25,
∴DE=,
故选:D.
5.解:在△CDF和△BCE中
∴△CDF≌△BCE(SAS)
∴∠CEB=∠CFD
∵∠DCF+∠CFD=90°
∴∠DCF+∠CEB=90°
∴∠EPC=90°
∴①正确;
如图延长CF交BA延长线于点M,
在△CFD和△MFA中
∴△CFD≌△MFA(ASA)
∴CD=MA=AB=a,
∵BP⊥CF
∴AP为Rt△MPB斜边BM上的中线,是斜边的一半,即AP=BM=×2a=a,
∴②正确;
∵CP⊥BE
∴CP×BE=CE×BC=
∵BE===
∴CP===
∴③正确
故选:D.
6.解:∵AB⊥AF,
∴∠FAB=90°,
∵点D是BC的中点,
∴AD=BD=BC,
∴∠DAB=∠B,
∴∠ADE=∠B+∠BAD=2∠B,
∵∠AEB=2∠B,
∴∠AED=∠ADE,
∴AE=AD,
∵BC=8,
∴AE=AD=4,
∵EF=,EF⊥AF,
∴AF===3,
故选:C.
7.解:
连接OB,过B作BM⊥x轴于M,
∵点B的坐标是(1,3),
∴OM=1,BM=3,由勾股定理得:OB==,
∵四边形OABC是矩形,
∴AC=OB,
∴AC=,
故选:C.
8.解:①∵EF=2,
∴OE=4,
∵AO=AB=6,
∴AE=AO+OE=6+4=10,故正确;
②∵∠AOC=90°,∠DOE=45°,
∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;
③作FG⊥CO交CO的延长线于G,
则FG=2,
∴△COF的面积S△COF=×6×2=6,故正确;
④作DH⊥AB于H,
CF==2,
BH=6﹣2=4,
DH=6+2=8,
BD==4,故错误.
故选:A.
9.解:连接DF,
∵EF为矩形ABCD的对角线BD的垂直平分线,AO=,
∴BD=2DO=2AO=,BF=DF,∠DOF=90°,
∴DO=,
在矩形ABCD中,∠C=90°,CD=AB=4,AD∥BC,
∴BD2=BC2+CD2,
即,
解得BC=6,
∵DF2=CF2+CD2,
∴DF2=(6﹣DF)2+42,
解得DF=,
∵EF垂直平分BD,
∴BO=DO,∠EOD=∠BOF=∠DOF=90°,
∵AD∥BC,
∴∠EDO=∠FBO,
∴△EDO≌△FBO(ASA),
∴OE=OF=EF,
在Rt△DOF中,DF2=OF2+OD2,
∴OF2+()2=()2,
解得OF=,
∴EF=.
故答案为.
10.解:如图所示,连接BF,CD,
∵四边形ABEF,四边形ACGD都是正方形,
∴AB=AF,AC=AD,∠BAF=∠CAD=90°,
∴∠BAD=∠FAC,
∴△BAD≌△FAC(SAS),
∴∠ACF=∠ADB,
又∵∠AHC=∠OHD,
∴∠CAH=∠DOH=90°,
∴CF⊥BD,
∴BC2=OB2+OC2,DF2=OD2+OF2,BF2=OB2+OF2,DC2=OD2+OC2,
∴BC2+DF2=OD2+OF2+OB2+OC2,
BF2+DC2=OD2+OF2+OB2+OC2,
即BC2+DF2=BF2+DC2,
又∵△ABF和△ACD都是等腰直角三角形,且AB=2,AC=4,
∴BF2+DC2=8+32=40,
∴BC2+DF2=40,
故答案为:40.
11.解:如图所示,过G作GH⊥AD,交AD的延长线于H,则∠H=90°,
又∵∠DCE=90°,
∴∠H=∠DCE,
∵四边形ABCD和四边形DEFG是正方形,
∴∠ADC=∠CDH=∠EDG=90°,DG=DE,
∴∠GDH=∠EDC,
∴△DGH≌△DEC(AAS),
∴GH=CE,
∵S正方形ABCD=6,
∴CD=,
∵S△ADG=,
∴AD×GH=,
又∵AD=CD,
∴CD×CE=,即×CE=,
∴CE=2,
∴Rt△CDE中,DE===,
∴S正方形DEFG=DE2=10,
故答案为:10.
12.解:延长NP交AB于H,
∵四边形ABCD为正方形,
∴∠BAC=90°,AB∥CD,
∵PN⊥CD,
∴PN⊥AB,
∴∠HAP=∠HPA=45°,
∴AH=PH,
设AH=PH=x,则BH=3﹣x,
在Rt△PBH中,PB2=PH2+BH2,
∴,
解得x=1或2,
当x=1时,BH=CN=2,在Rt△BCN中,;
当x=2时,BH=CN=1,在Rt△BCN中,.
故答案为或.
13.解:分两种情况:
①如图1所示,当点F在AD上时,
由CF=BE,CD=BC,∠BCE=∠CDF=90°可得,Rt△BCE≌Rt△CDF(HL),
∴∠DCF=∠CBE,
又∵∠BCF+∠DCF=90°,
∴∠BCF+∠CBE=90°,
∴∠BMC=90°,即CF⊥BE,
∵BC=4,CE=3,∠BCE=90°,
∴BE=5,
∴CM==;
②如图2所示,当点F在AB上时,
同理可得,Rt△BCF≌Rt△CBE(HL),
∴BF=CE,
又∵BF∥CE,
∴四边形BCEF是平行四边形,
又∵∠BCE=90°,
∴四边形BCEF是矩形,
∴CM=BE=×5=.
故答案为:或.
14.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△DFP=S△PBE=×2×8=8,
∴S阴=8+8=16,
故答案为16
15.解:如图,连接BF,作FH⊥BE于H.作FM∥BE交BC于M.
∵四边形ABCD是矩形,
∴AB=CD=4,∠D=∠C=∠ABC=90°,
∵F是CD中点,
∴DF=FC=2,
∵EF平分∠BED,FH⊥EB,FD⊥ED,
∴FH=FD=FC,
∵BF=BF,
∴Rt△BFH≌Rt△BFC,
∴∠FBC=∠FBE,
∵BE平分∠ABC,
∴∠ABE=45°,
∴∠FBC=∠FBH=22.5°,
∵FM∥BE,
∴∠FMC=∠EBC=45°,
∵∠FMC=∠FBM+∠MFB,
∴∠MFB=∠MBF=22.5°,
∴FM=BM,
∵∠FMC=∠CFM=45°,CF=2,
∴FM=BM=2,
∴BC=BM+CM=2+2.
故答案为2+2.
16.解:∵四边形ABCD是正方形,△CDE是等边三角形,
∴AD=CD=DE;∠ADE=90°+60°=150°,
∴∠AED=(180°﹣150°)÷2=15°.
同理可得∠CEB=15°,
∴∠AEB=∠DEC﹣∠DEA﹣∠CEB=30°.
故答案为:30°.
17.解:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CF⊥BD,
∴CF⊥AG,
又∵点D是AC中点,
∴BD=DF=AC,
∴四边形BGFD是菱形,
∴GF=BG=5,则AF=13﹣5=8,AC=2×5=10,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即82+CF2=102,
解得:CF=6.
故答案是:6.
18.解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=90°,AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴∠BAE=∠DAH=45°,
∴△ABE和△ADH是等腰直角三角形,
∴AE=AB,AD=AH,
∵AD=AB=AH,
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,
∴①正确;
在△ABE和△AHD中,,
∴△ABE≌△AHD(AAS),故②正确;
∴BE=DH,
∵AB=AH,
∵∠AHB=(180°﹣45°)=67.5°,
∴∠OHE=∠AHB=67.5°,
∴∠DHO=90°﹣67.5°=22.5°,
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,,
∴△BEH≌△HDF(ASA),
∴BH=HF,故③正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故④错误;
过H作HK⊥BC于K,
可知KC=BC,HK=KE,
由上知HE=EC,
∴BC=KE十EC,
又KE=HK=FC,HE=EC,
故BC=HK+HE,BC=2HK+2HE=FC+2HE
∴⑤正确;
故答案为:①②③⑤.
19.解:(1)如图甲所示:
∵EA=EF,
∴△AEF是等腰直角形,∠EAF=∠EFA,
∵∠EAF=45°,
∴∠EFA=45°,
又∵在△AEF中,∠EAF+∠EFA+∠AEF=180°,
∴∠AEF=180°﹣45°﹣45°=90°,
又∵∠AEB+∠AEF+∠FEC=180°,
∴∠AEB+∠FEC=90°,
又∵△ABE中,∠B+∠BAE+∠AEB=180°,
∠B=90°,
∴∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
在△ABE和△ECF中
,
∴△ABE≌△ECF(AAS)
∴AB=EC,BE=CF,
又∵AB=3,BC=4,
∴EC=3,CF=1,
在Rt△CEF中,由勾股定理得:
==
故答案为.
(2)如图乙所示:
作DM=DF,BN=BE,分别交AD,AB于点M和点N,设MD=x,
∵四边形ABCDA是矩形,
∴∠B=∠D=90°,
∴∠BNE=45°,∠DMF=90°,
又∵∠BNE+∠ENA=180°,∠FMD+∠FMA=180°,
∴∠ENA=135°,∠FMA=135°,
又∵∠EAF=45°,∠BAD=∠BAE+∠EAF+∠FAD=90°,
∴∠BAE+∠FAD=45°,
∵∠BAE+∠NEA=45°,
在△ANE和△FMA中
,
∴△ANE∽△FMA(AA)
∴;
又∵MD=x,∴DF=x,
∵CE=CF,AB=3,BC=4,
∴FC=EC=3﹣x,BE=AB=x+1,AN=2﹣x,
∴,
解得:2﹣4,或﹣2﹣4(舍去),
∴FC=3﹣()=7﹣2,
∴EF=FC=(7﹣2)=7﹣4.
故答案为7﹣4.
20.解:连接AC交BD于点O,如图所示:
(1)∵四边形ABCD是正方形,
∴AB=BC=CD,∠ABE=∠CBE=∠CDF,
又∵CF∥AE,
∴∠AEF=∠CFE,
又∵∠AEF+∠AEB=180°,∠CFE+∠CFD=180°,
∴∠AEB=∠CFD,
在△ABE和△CDF中,
,
∴△AEB≌△CFD(AAS);
(2)∵△AEB≌△CFD,
∴AE=CF,
∴四边形AECF是平行四边形,
在△ABE和△CBE中
,
∴△ABE≌△CBE(SAS)
∴AE=EC,
∴?AECF是菱形;
(3)∵AB=4,AB=BC=CD,
∴在Rt△BCD中,由勾股定理得,
BD===,
又∵BD=BE+ED,DE=3,
∴BE=
又∵BE=DF,
∴DF=,EF=,
又∵AC=BD,
∴AC=4,
∴==8
故答案为8.
21.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
22.(1)解:∵∠A=60°,AG=AE,
∴△AGE是等边三角形,
∴∠AGE=60°,
∴∠EGB=120°;
(2)证明:由(1)知,∠EGB=120°,
∵四边形ABCD为菱形,
∴AB∥CD,AB=AD,
∴∠A+∠D=180°,
∵∠A=60°,
∴∠D=120°,
∴∠DEF+∠DFE=60°,
∴∠D=∠EGB,
∵△AGE是等边三角形,
∴AE=AG,∠AEG=60°,
∴DE=GB,
∵∠BEF=60°,
∴∠DEF+∠GEB=60°,
∴∠DFE=∠GEB,
∴△DFE≌△GEB(ASA),
∴EF=BE;
(3)解:∵△DFE≌△GEB,
∴DF=GE,
当EG=EP时,过E作EM⊥AB 垂足为M,
设AE=x,
∵△AGE是等边三角形,
∴AM=x,EM=x,
∴BM=4﹣x,
∵P为EF的中点,
∴EF=2EP,
由(2)知EF=BE,
∴EB=2EG=2AE=2x,
在Rt△EBM中,EM2+BM2=EB2,
即(x)2+(4﹣x)2=(2x)2,
解得,(舍去),
即AE=;
当EG=GP时,过G作GQ⊥EF,垂足为Q,过B作BH⊥CD垂足为H,连接BF,设AE=x,
∵△AGE是等边三角形,
∴EG=x,
∵EF=EB,∠BEF=60°,
∴△BEF为等边三角形,
∴∠EFB=∠BEF=60°,EF=BF,
∵△BEG≌△EFD,
∴∠BEG=∠EFD,DF=EG,
∴∠GEQ=∠BFH,CF=4﹣x,
∵∠EQG=∠FHB=90°,
∴△EGQ∽△FBH,
∴EG:BF=EQ:FH,
设△BEF的边长为a,
则BF=EF=a,
∵P为EF的中点,
∴EP=a,
∵EG=GP=x,
∴EQ=EP=a,
在Rt△BCH中,BC=AB=4,∠C=∠A=60°,
∴CH=2,
∴BH=,
∴HF=2﹣(4﹣x)=x﹣2,
∵BF2=BH2+HF2,
∴a2=()2+(x﹣2)2,
∵EG:BF=EQ:FH,
∴,
即a2=4x2﹣8x,
∴
解得,(舍去),
即AE=;
当EP=GP时,点P在EG的中垂线上,即P点AC上,
而运动期间P不可能位于线段AC上,
∴P在AC上不存在,
综上,AE=或;
即当AE为或时,△EGP是等腰三角形.
23.证明:(1)∵DE∥AC,CE∥BD,
∴四边形DOCE是平行四边形,
∵矩形ABCD的对角线AC,BD相交于点O,
∴AO=CO=DO=BO,
∴四边形OCED为菱形.
(2)过O作OE⊥BC,
∵矩形ABCD的对角线AC、BD相交于点O,
∴OA=OB,
∵AF垂直平分线线段BO于点F,
∴AB=AO,
∴△ABO是等边三角形,
∴∠AOB=60°,
∴∠BOC=120°,
∴∠BOE=60°,
∴∠OBE=30°,∠OEB=90°,
∴BE=,
∴BC=6.
24.(1)证明:∵四边形ABCD为矩形,
∴AD∥BC,∠DAB=∠ABE=90°,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠BAE=∠AEB=45°,
∴AB=EB,
∵DF⊥AC
∴∠AFD=90°,
∴∠ABE=∠AFD=90°,
∵AE=AD,
∴△ABE≌△AFD(AAS),
∴AB=AF;
(2)①证明:∵AE=AD,∠EAD=45°,
∴∠AED=∠ADE=67.5°,
∴∠FDG=22.5°,
∵AB=AF,∠BAF=45°,
∴∠AFB=67.5°,
∴∠EFG=67.5°,
∴∠EFG=∠AED,
∴FG=EG,∠DFG=22.5°,
∴∠DFG=∠FDG,
∴FG=DG,
∴EG=DG;
②解:∵EG=1,
∴ED=2,
设AB=x,则AE=,DF=AF=x,
∴EF=﹣x,
∴(﹣x)2+x2=22,
解得x2=,
∴矩形ABCD的面积==.
25.(1)证明:∵ABCD是正方形,
∴∠C=90°,
∵PE⊥CD,PF⊥BC,
∴四边形PFCE是矩形,
∴EF=PC,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴AP=CP;
(2)解:∵由(1)知△ABP≌△CBP,
∴∠BAP=∠BCP=60°,
∴∠PCE=30°,
∵四边形ABCD是正方形,BD是对角线,
∴∠PDE=45°,
∵PE⊥CD,
∴DE=PE,
∵PD=,
∴PE=1,
∴PC=2PE=2.
26.解:(1)证明:
∵AF平分∠BAD,
∴∠BAF=∠DAF,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAF=∠CEF,∠BAF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
又∵四边形ECFG是平行四边形,
∴四边形ECFG为菱形;
(2)①∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,AD∥BC,
∵∠ABC=120°,
∴∠BCD=60°,∠BCF=120°
由(1)知,四边形CEGF是菱形,
∴CE=GE,∠BCG=∠BCF=60°,
∴CG=GE=CE,∠DCG=120°,
∵EG∥DF,
∴∠BEG=120°=∠DCG,
∵AE是∠BAD的平分线,
∴∠DAE=∠BAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,
∴BE=CD,
∴△DGC≌△BGE(SAS);
②∵△DGC≌△BGE,
∴BG=DG,∠BGE=∠DGC,
∴∠BGD=∠CGE,
∵CG=GE=CE,
∴△CEG是等边三角形,
∴∠CGE=60°,
∴∠BGD=60°,
∵BG=DG,
∴△BDG是等边三角形,
∴∠BDG=60°;
(3)如图3中,连接BM,MC,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形.
∵∠BAF=∠DAF,
∴BE=AB=DC,
∵M为EF中点,
∴∠CEM=∠ECM=45°,
∴∠BEM=∠DCM=135°,
在△BME和△DMC中,
∵,
∴△BME≌△DMC(SAS),
∴MB=MD,
∠DMC=∠BME.
∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,
∴△BMD是等腰直角三角形.
∵AB=8,AD=14,
∴BD=2,
∴DM=BD=.
过M作MH⊥DF于H,
∵∠ABC=90°,四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
又由(1)可知四边形ECFG为菱形,
∠ECF=90°,
∴四边形ECFG为正方形,
∴∠CEF=45°,
∴∠AEB=∠CEF=45°,
∴BE=AB=8,
∴CE=CF=14﹣8=6,
∵MH∥CE,EM=FM,
∴CH=FH=CF=3,
∴MH=CE=3,
∴DH=11,
∴DM==.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
